“思想共生、素养共长、文化共育”数学教学探究*

岳绍杰|山东省东营市东营区教学研究室

于 彬|山东省东营市胜利第六中学

蒋立国|山东省东营市东营区黄河中学

《义务教育数学课程标准（2022 年版）》（以下简称“《课程标准》”）明确了核心素养的内涵及主要表现，提出要让学生“获得适应未来生活和进一步发展所必需的数学基础知识、基本技能、基本思想、基本活动经验”，要求“关注数学学科发展前沿与数学文化，继承和弘扬中华优秀传统文化”.然而，当前数学课堂教学中“重知识、轻素养、缺文化”的现象仍然普遍存在，这是因为一线教师并未足够重视对学生进行“思想的渗透、素养的培育、文化的浸润”.基于此，笔者以参加山东省“黄河文化育人资源的整合与运用”现场会为契机，设计并展示了“认识二元一次方程组”一课，旨在落实《课程标准》提出的新理念，实现“思想共生、素养共长、文化共育”，下面详细介绍.

一、“思想共生、素养共长、文化共育”下的内容及教学解析

（一）内容解析

“认识二元一次方程组”是北师大版义务教育教科书《数学》八年级上册第五章的内容，是该章起始课，旨在引导学生感受二元一次方程（组）学习的必要性，及其在解决问题中的优越性等.二元一次方程组是一类最简单的线性方程组，它是刻画现实世界数量关系的一个有效数学模型，也是学习数学乃至物理、化学等其他学科知识的重要基础.“认识二元一次方程组”一课既是一元一次方程的延续，又是进一步学习其他方程的前提，与研究一元一次方程的“基本套路（定义、解法、应用）”相同.该课蕴含丰富的数学思想、数学素养、数学文化.

数学思想：方程是刻画现实世界数量关系的有效模型、类比思想、建模思想.

数学素养：模型观念、运算能力、应用意识.

数学文化：该章“章前图”为学生呈现了古老的数学问题——鸡兔同笼；该章第1、2个情境分别以图文并茂的形式为学生呈现了《希腊文选》中记录的“欧几里得问题”及现实生活中的“购票问题”.

此外，该章引言为学生提供了内容学习的路径和方法，该章第2 个情境还意在引出“二元一次方程（组）解”的概念，教师应对其有足够的重视.

立足上述分析，为体现单元整体设计和学科育人理念，笔者结合本地实际情况，创设“‘保护湿地生态传承黄河文化’主题研学旅行”大情境，在保证实现该章第1、2 个情境目的的基础上，着重引导学生于欣赏家乡美的同时，领略黄河文化的魅力，感受环境保护的必要性，并确定这节课的教学重点：了解二元一次方程（组）的概念及其解的意义.

（二）教学目标及解析

《课程标准》对这节课的要求是：能根据现实情境理解（二元一次）方程的意义，能针对具体问题列出（二元一次）方程；理解（二元一次）方程解的意义.由此，笔者设计这节课的教学目标并作解析.

1.教学目标

目标1：在具有文化意味的情境问题的解决中，再次感受（二元一次）方程是刻画现实世界数量关系的有效模型.

目标2：在具有文化意味的情境问题的解决中，概括二元一次方程（组）的概念；体会二元一次方程（组）解的意义.

目标3：在具有文化意味的研学过程和课堂学习中，培养保护环境和自强爱国的个人情怀，培育模型观念、运算能力、应用意识等核心素养.

2.目标解析

目标1达成的标志是：学生能在具体情境中发现两组等量关系，并在灵活设置未知数的基础上，准确列出方程.

目标2达成的标志是：学生能通过相应的探究活动说出二元一次方程（组）的概念；学生能说出二元一次方程（组）解的概念，并能判断出一组数是不是某个二元一次方程组的解.

目标3达成的标志是：学生能感受到“数学来源于生活，又服务于生活”，体会到二元一次方程（组）学习的必要性，及其在解决问题中的优越性；学生能在具体情境和问题解决中种下“保护环境”和“自强爱国”的种子，逐渐成长为“有理想、有本领、有担当”的“三有”时代新人.此目标属于情感、态度与价值观方面的目标，需要在长期过程中慢慢形成.

（三）教学问题解析

通过一元一次方程相关内容的学习，学生基本具备了在具体情境中寻求一组等量关系的能力，能够用一元一次方程解决现实生活中的实际问题，具备了学习新方程的能力和条件，但学生对“元”和“次”的认识，仅限于“一元”“一次”的感性认识，且难以利用方程表示相对复杂的等量关系.学生已有基础及其与目标的差距分析如表1所示.

表1 学生已有基础及其与目标的差距分析

通过上述分析，笔者确定这节课的教学难点：在具体情境中，发现（两组）等量关系，列出二元一次方程（组）.

二、“思想共生、素养共长、文化共育”数学教学设计说明

（一）思想共生

《课程标准》要求培养学生的数学基础知识、基本技能、基本思想和基本活动经验，而由于思想具有再生性，教学中对基本思想的渗透至关重要.

教师可先引导学生在回顾一元一次方程知识的基础上，通过类比思想，帮助学生自主建构二元一次方程（组）的基础知识（定义及其解的概念），然后在小结中为其他方程的学习进行“预设”，以充分体现类比思想的重要作用.教师应将建模思想贯穿教学始终，化解学生后续在“应用”学习中的压力，以实现类比思想和建模思想等不同数学思想的共生.

（二）素养共长

在中国学生发展核心素养方面：先引导学生欣赏诸如“山东黄河三角洲国家级自然保护区”的宣传片，感受环境保护的必要性，培养“责任担当”素养；再引导学生通过类比的方法，自行归纳二元一次方程（组）的定义及其解的概念，积极践行“学会学习”素养的培育；最后，设计多个反思环节，引导学生及时进行梳理总结，将新知纳入原有知识体系，争做“勤于反思”的好学生.

在数学学科核心素养方面：先引导学生用数学的眼光观察现实世界，在相关情境中提出数学问题；再引导学生用数学的思维思考现实世界，并提供类比这一思维支架，使其展开自主思考和探究；最后引导学生用数学的语言表达现实世界，用自己的语言自行归纳并获得二元一次方程（组）的定义及其解的概念.

教师要通过相关问题的解决和情境的分析，培育学生模型观念、应用意识等核心素养，为落实《课程标准》的总体目标和要求进行积极的探索和实践，实现中国学生发展核心素养和数学学科核心素养的共长，或学生数学学科各核心素养的共长.

（三）文化共育

中华文明源远流长，孕育了中华民族的优秀精神品格，培育了中国人民的崇高价值追求，在课堂教学中具有很好的育人价值.2021年2 月，《中华优秀传统文化进中小学课程教材指南》正式颁布，标志着传统文化进课堂势在必行.

为更好地发挥数学学科的育人价值，教师要充分挖掘地域文化，如可通过“‘保护湿地生态传承黄河文化’主题研学旅行”这一大情境，引导学生在知识掌握的同时，感受黄河文化中所蕴含的“家国天下、自强不息、崇德尚义、乐知天命、兼收并蓄”等内涵精髓.教师应充分发挥数学学科本身所具有的理性精神，在问题探究和解决中，培养学生严谨的数学思维和坚毅的数学品格.此外，教师还要融入部分数学文化类题目（欧几里得问题、鸡兔同笼问题等），使学生在耳濡目染中提升文化认同和文化自信，实现数学文化和黄河文化的共育.

三、“思想共生、素养共长、文化共育”数学教学设计案例

笔者以“思想共生、素养共长、文化共育”为视角，尝试对“认识二元一次方程组”进行教学设计.

（一）创设情境，疑点反思

笔者播放“山东黄河三角洲国家级自然保护区”的宣传片，创设“‘保护湿地生态传承黄河文化’主题研学旅行”大情境，并将之细化为若干小情境，引导学生感受家乡美，学会用数学的眼光观察现实世界，并从中发现或提出数学问题.

［情境1］已知某研学小组师生共6 人，买门票花费240 元（成人门票60 元，学生半价），根据这些情况，你能提出哪些数学问题?

［预设］教师和学生分别有多少人？用一元一次方程解决（设一个未知数），但有部分学生可能会设两个未知数.

［情境2］同学们乘坐景区内游船，体验“黄蓝交汇”的旷世奇观.1艘东方白鹳号游船可乘坐16人，1艘丹顶鹤号游船可乘坐22人.丹顶鹤号游船数的一半比东方白鹳号游船数的2倍少1，两种游船共载164人，每艘游船没有空位.根据这些情况，你能提出什么数学问题？

［预设］各有多少艘游船？尝试用一元一次方程解决，但是对部分学生来说存在一定困难；进而设两个未知数，抽象等量关系，列出方程.

［师生活动］通过教师引导和学生自主探究，学生在情境1和情境2中抽象出等量关系，然后列出方程.情境1 可用“设一个未知数或两个未知数”的方法轻松得到方程；情境2 在用“设一个未知数”解决时可能会存在一定的困难，所以教师可引导学生“设两个未知数”，通过等量关系列出方程.

设计说明：以有关联的两组情境，引导学生由易到难，在逐步应用类比思想解决问题的过程中，去体会建模思想，为实现“思想共生”奠定基础.通过“‘保护湿地生态传承黄河文化’主题研学旅行”这一大情境，引导学生在“购票”和“乘坐游船”等实际问题中，发现或提出数学问题，让学生用数学的眼光观察现实世界，培育学生的数学学科核心素养，同时引导学生在感受“黄河之水天上来，奔流到海不复回”的壮观和欣赏“山东黄河三角洲国家级自然保护区”美景的过程中，感受家乡的美丽富饶、祖国的繁荣昌盛，培养“爱祖国爱家乡”的家国情怀，实现中国学生发展核心素养的培育，由此为实现“素养共长”奠定基础.该环节还渗透黄河文化，为后续实现“文化共育”奠定坚实的基础.

（二）尝试解疑，问题反思

［任务1］复习一元一次方程，了解其定义、解法、应用.

［预设及师生活动］教师搭建脚手架，引导学生回忆“元”和“次”的概念.在情境1的基础上，学生回忆一元一次方程学习的“基本套路”，并在“问”和“追问”中重建已有知识体系，明晰“元”和“次”的概念.随后，教师出示这节课的教学目标.

设计说明：回忆一元一次方程中“元”和“次”的概念，引导学生利用类比思想，为后续顺利建构二元一次方程（组）的概念作铺垫，体现“思想共生”.学生在重建知识体系的过程中，可加强会用数学的思维思考现实世界的能力，并能为后续会用数学的语言表达二元一次方程（组）及其解的概念奠定基础，体现“素养共长”.此外，出示教学目标，渗透这节课及整章的研究思路和方法，能体现知识的系统性和一致性.

（三）问题解决，应用反思

【任务2】二元一次方程的定义.

观察思考：以上几个方程具有哪些共同特征？

［预设及师生活动］在类比一元一次方程定义的基础上，学生可以轻松地用自己的语言给出二元一次方程的定义；教师以“追问”引导学生进行完善，进而获得准确的定义.

设计说明：引导学生在类比的基础上，自行归纳获得二元一次方程的定义，体现“思想共生”.

［任务3］二元一次方程组的定义.

问题1：在情境1 中得到的两个方程中，x所代表的对象相同吗？y呢？

问题2：在情境2 中得到的两个方程中，x所代表的对象相同吗？y呢？

［预设及师生活动］上述问题要求学生独立完成.学生在“脚手架”问题的指导下，给出问题的答案，并自行归纳二元一次方程组的定义.教师进行完善和补充.

设计说明：以问题的形式呈现，引发学生自主探究的欲望，在对二元一次方程组定义的自行归纳、完善中，不断提高学习能力和反思能力，发展数学学科核心素养，体现“思想共生”“素养共长”.

［任务4］二元一次方程（组）的解.

问题3：在考虑情境1实际情况的前提下，你能找到哪些x、y的值适合方程x+y＝6？你有什么发现？

问题4：如果不考虑情境1的实际情况，你还能找到哪些x、y的值适合方程x+y＝6？你有什么发现？

［预设及师生活动］在教师提示性问题的引导下，学生自主完成表格（略）填写，并获得相关结论.

设计说明：引导学生在具体情境和数学问题中，感受二元一次方程解的意义，加深印象，并运用类比的方法自行归纳其解的概念，体现“思想共生”.

问题5：按照同样的方法，你能找到哪些x、y的值适合方程60x+30y＝240？

问题6：对比两个表格（如图1所示），你有什么发现？

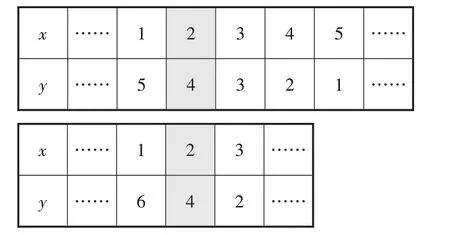
图1 x+y＝6与60x+30y＝240的解对照表

［预设及师生活动］在教师提示性问题的引导下，学生自主完成表格填写并获得结论.

设计说明：引导学生类比一元一次方程的定义及解的概念，获得二元一次方程（组）的定义及解的概念，体现“思想共生”.同时，运用类比的方式还在于引导学生“学会学习”，使其在会用数学的语言表达现实世界的基础上，发展中国学生发展核心素养，进而实现“素养共长”.

（四）课堂练习，方法反思

练习1：如果关于x、y的方程2xm-1-y4+n=7是二元一次方程，则m＝___，n＝___.

练习2：判断下列方程组是否是二元一次方程组？并说明理由.

练习3：下面4组数值中，哪些是二元一次方程2x+y＝10的解？

练习4：根据题意列出方程组：驴子和骡子驮着货物并排走在路上，驴子不停地埋怨驮的货物太重，压得受不了.骡子对驴子说：“你发什么牢骚啊！我驮的比你驮的更重.倘若你的货给我1口袋，我驮的货比你驮的货重1倍；而我若给你1口袋，咱俩才刚好一样多.”驴子和骡子各驮几口袋货物？（欧几里得问题，出自《希腊文选》）

［预设及师生活动］学生独立完成，教师适时点拨.

设计说明：通过练习1～3 巩固二元一次方程（组）及其解的定义，将新知纳入原有知识体系；练习4 以数学文化题的形式呈现，引导学生在感受黄河文化源远流长的基础上，进一步体会数学文化的博大精深，培养学生的学习兴趣和爱好.该环节引导学生巩固二元一次方程及二元一次方程组的定义及其解的概念，体现“思想共生”；同时，引入数学文化，实现数学文化和前述黄河文化的“文化共育”.

（五）课堂总结，提升反思

追问1：这节课的知识，你是怎么得到的？

追问2：你掌握的方法能解决什么问题？

追问3：你在哪些方面还有待加强？

追问4：你还要学习什么？

［预设及师生活动］教师以“追问”的形式给出问题，帮助学生进一步明确这节课需要掌握的知识、思想、方法，以及后续需要研究的内容.教师引导学生在回顾这节课所学知识的同时，初步建构整章甚至整个初中阶段“方程、不等式、函数”的学习体系（如图2 所示），体现《课程标准》提出的单元整体教学理念.

图2“方程、不等式、函数”的学习体系

设计说明：将方程的学习置于整个初中阶段“数与代数”的学习，引导学生运用类比思想建构知识体系，体现“思想共生”.以追问1和2引导学生反思回顾这节课的学习过程，为学生课后预习指明思路.以追问3 和4 引导学生反思这节课需要提高的地方，比如回答问题的积极性、解决问题的严密性等，为学生后续学习奠定基础，指向“学会学习”.在培育学生模型观念、运算能力、应用意识等核心素养的同时，也培育了责任担当、家国情怀等中国学生发展核心素养，从而实现“素养共长”.

［教师寄语］黄河文化的丰富内涵包括家国天下、自强不息、崇德尚义、乐知天命、兼收并蓄等.作为青少年的我们，要厚植家国情怀、涵养进取品格，以奋斗姿态激扬青春，不负时代，不负华年.

设计说明：通过教师寄语，引导学生体会二元一次方程（组）在解决现实生活问题中所发挥的重要作用，进而喜欢数学.同时，与开课之初前后照应，再次渗透黄河文化，体现“文化共育”，建构“数学思政、立德树人”的闭环，引导学生争做“有理想、有本领、有担当”的时代新人.

（六）布置作业，梳理反思

达标检测作业如下.

（1）下列不是二元一次方程组的是（）

（3）根据题意列出方程组：今有鸡兔同笼，上有35头，下有94足，问鸡兔各几何？（鸡兔同笼问题，出自我国古代数学名著《孙子算经》）

基础作业及实践作业如下.

（1）基础作业：共10 题，其中选择题4 题，填空题3题，解答题3题，每种题型里面分层呈现（要求当天完成，限于篇幅，此处省略）.

（2）实践作业（任选一题完成）：

①结合研学之旅，根据具体情境（参考情境1或情境2），自编一个可以用二元一次方程组来解决的实际问题.

②尝试在我国古代数学著作《孙子算经》或《九章算术》中找出一个可以用二元一次方程组来解决的实际问题.

［预设及师生活动］学生独立完成达标检测作业，教师公布答案，学生交换批改.在达标检测作业中设计“鸡兔同笼”问题，意在引导学生进一步感受我国古代数学文化的博大精深.对短作业（基础作业），学生要在课后20 分钟内完成.长作业（实践作业）贯穿该章学习的始终，其中第①题与这节课创设的情境一致，旨在引导学生持续发现现实生活中的数学问题，第②题体现这节课设计的“数学文化”线，旨在引导学生自主探究，提高学习能力和学习兴趣，为后续二元一次方程组解法的学习作铺垫.

设计说明：通过一组练习巩固这节课学习的“二元一次方程（组）”，实现“堂堂清、日日清”.作业是学生巩固知识、形成能力、培养习惯的重要载体，也是教师了解学情、完善教学管理的重要手段.在“双减”背景下，上述作业设计力求做到“让不同的学生得到不同的发展”，并体现以下指导思想：控制数量，提高质量；分层作业，面向全体；注重基础，培育素养.在达标检测中，引导学生勤于反思，形成中国学生发展核心素养，同时深化应用意识等数学学科核心素养，实现“素养共长”.此外，该环节回应课堂教学的主线，给出两个实践作业，一个指向“黄河文化”，一个指向“数学文化”，从而进一步实现“文化共育”，将学科育人落到实处.

综上，笔者以“思想共生、素养共长、文化共育”为设计理念，分析教材相关内容所蕴含的数学思想、数学素养、数学文化，根据中国学生发展核心素养与数学学科核心素养的培育要求，有机融入本土文化，给出了“认识二元一次方程组”的教学设计思路与方案.在教学实践中，笔者发现，这能有效地激发学生的学习兴趣，使其在文化的浸润中自觉主动地进行探究性学习，进而体会数学思想的奥妙，发展高阶思维，涵养家国情怀，提升责任担当意识.笔者期待能有更多的同行参与进来，给出更多富有思想、素养、文化的精彩课例，为初中数学乃至其他学科教学的高质量发展贡献力量.