考虑吊杆断裂的拱梁组合桥动力响应分析

吴庆雄, 郑樵风, 尹永胜, 黄昌浩, 朱建瑞

(1. 福州大学土木工程学院, 福建 福州 350108; 2. 山东高速高商公路有限公司, 山东 济南 251600)

0 引言

近20年来, 钢管混凝土拱桥在我国道路建设中被广泛应用[1]. 根据悬吊桥面系相对于拱肋的位置, 可以分成上、 中和下承式3种类型. 随着拱桥修建数量和年限的不断增加, 采用吊杆将桥面系荷载传递给拱肋的中、 下承式钢管混凝土拱桥安全问题已逐渐显现. 主要因吊杆所用材质为高强钢索, 且桥面系所承受荷载通过吊杆传递, 故在桥面系所承受的变幅车辆荷载和外部环境下, 对吊杆的自然损伤会导致吊杆更容易出现疲劳或腐蚀断裂. 据不完全统计, 近年来, 仅国内就发生了5起中、 下承式钢管混凝土拱桥因吊杆断裂而导致的落梁甚至坍塌的事故[2-4], 造成的损失不言而喻.

为此, 中、 下承式钢管混凝土拱桥吊杆断裂问题应进行深入研究, 以期在桥梁设计阶段就充分考虑桥面系强健性, 避免吊杆断裂造成的落梁等事故. 根据拱桥桥面系结构与受力特点, 按桥面系强健性等级可分为3大类[5]. 中、 下承式钢管混凝土拱桥大多属于超静定结构, 较多使用第2、 3类悬吊桥面系. 余印根[6]、 吴庆雄等[7]、 陈康明等[8]针对2类悬吊桥面系拱桥断索问题开展深入研究; 邓育林等[9]、 Shao等[10]、 于博等[11]则以第3类悬吊桥面系拱桥断索问题进行研究. 上述学者主要研究吊杆断裂位置、 断索时长等对拱桥剩余结构受力性能影响, 提出采用等效静力计算法进行第2、 3类悬吊桥面系拱桥动力响应计算, 获取具有代表性的动力系数.

拱梁组合桥属于外部静定, 内部超静定的结构. 在3类悬吊桥面系拱桥中, 拱梁组合桥是整体性、 强健性最好的结构, 但该类桥型同样存在断索的隐患. 截至目前, 所收集的文献中并没有对拱梁组合桥断索问题展开深入分析, 仅余印根[12]建议对于拱梁组合桥的强健性设计可参照《公路斜拉桥设计细则(JTG D65-01—2007)》[13]第6.2.1条第8款: “在斜拉桥结构计算中, 至少应确保一根斜拉索脱落或断索后, 主梁最大应力增加不应超过相应设计应力的10%”. 然而, 拱梁组合桥的桥面系仍由系梁、 横梁和桥面板构成, 与斜拉桥采用的连续主梁结构不完全相同, 故该建议的合理性有待进一步验证.

本研究以拱梁组合桥为研究对象, 通过统计拱梁组合桥的参数, 构建具有代表性的标准拱梁组合桥, 采用有限元软件ANSYS/LS-DYNA进行吊杆断裂冲击作用下拱梁组合桥动力分析, 得到剩余结构的动力响应, 并获取具有普适性的拱梁组合桥动力系数, 为后续拱梁组合桥等效静力方法设计计算提供参考.

1 拱梁组合标准桥的构建

目前, 作者课题组已收集到98座拱梁组合桥相关资料. 其中, 跨径超过125 m的拱梁组合桥仅有5座, 跨径最大的为河南岭南高速公路蒲山大桥, 跨径为225 m. 拱梁组合桥按照跨径分为4种类别: 50 m≤L<75 m、 75 m≤L<100 m、 100 m≤L<125 m、L≥125 m. 各跨径范围内桥梁数量占比分别为32.7%、 45.9%、 16.3%、 5.1%, 多数拱梁组合桥跨径集中在50～125 m, 占总数的94.9%. 拱梁组合桥的主要参数有: 矢跨比、 拱轴线形、 拱肋截面形式、 拱肋钢材、 管内混凝土材料等. 为保证构建的拱梁组合标准桥与实际工程中拱梁组合桥构造相似, 以98座CFST拱梁组合桥为分析对象, 数据统计了各跨径范围内拱梁组合桥的主要参数. 限于文章篇幅, 本研究仅给出75～100 m跨径的统计数据, 如表1所示.

表1 跨径75～100 m拱梁组合桥参数统计Tab.1 Statistical of composite bridge parameters for arch-girder combined bridges with span from 75 to 100 m

根据各跨径范围内的参数统计结果, 构建50、 60、 …、 120 m标准跨径的拱梁组合标准桥, 以跨径100 m拱梁组合标准桥为例进行说明. 拟定跨径100 m拱梁组合标准桥的计算跨径100 m, 矢跨比1/5, 拱轴线形采用二次抛物线, 拱肋采用哑铃形截面, 拱肋截面高度2.7 m, 钢管直径采用1 100 mm, 钢管壁厚16 mm, 哑铃形腹板厚16 mm, 钢材采用Q345, 管内填充C50混凝土. 横撑由中间一道一字型横撑和两边各一道K撑组成. 系梁为箱梁截面, 采用C50混凝土, 梁宽150 cm, 梁高230 cm. 中横梁为箱梁截面, 采用C50混凝土, 梁宽150 cm, 梁高145 cm. 端横梁为箱梁截面, 采用C50混凝土, 梁宽400 cm, 梁高320 cm. 桥面板采用空心板, C50混凝土, 板高30 cm, 板宽124 cm. 吊索采用FES(FD)7-85低应力防腐索体, 吊杆间距为5.5 m.

利用桥梁通用软件MIDAS/CIVIL建立空间杆系有限元模型, 对构建的跨径100 m拱梁组合标准桥进行结构受力验算. 对各跨径拱梁组合标准桥进行拱肋强度、 稳定承载能力、 系梁和吊杆承载能力、 全桥弹性稳定等方面的验算, 结果如表2所示. 由表2可见, 100 m跨径的拱梁组合标准桥满足要求.

表2 跨径100 m拱梁组合标准桥验算结果Tab.2 Checking results of standard arch-girder combined bridge with a span of 100 m

对吊杆断裂的拱梁组合桥进行结构动力响应分析时常采用拆除构件法. 拆除构件法的原理是将结构的关键支撑构件移除, 通过分析剩余结构的动力响应变化来确定被分析结构的最不利的破坏模式[14]. 拆除构件法根据实现方法不同可分为动态分析计算方法和静态分析计算方法. 本研究采用考虑吊杆断裂动力作用的拱梁组合桥等效静力计算法,如图1所示. 假设当第i对吊杆断裂时, 在断裂吊杆吊点拱肋端和系梁端施加一对反向集中力(ND), 由此集中力来考虑吊杆断裂冲击作用. 在进行等效静力法计算时, 假定吊杆断裂所产生的冲击力ND仅由断裂吊杆初始力(N0,N0按承载能力极限状态下恒载和活载的最不利组合确定[8])的冲击作用引起[15], 引入动力系数(μD), 考虑吊杆断裂冲击作用, 得到

图1 考虑吊杆断裂动力作用的等效静力法Fig.1 Equivalent static method with suspenders dynamic effect

ND=μD·N0

(1)

从式(1)可知,ND能否准确等效动力响应,μD的取值至关重要. 因此, 基于具有代表性的拱梁组合标准桥, 开展吊杆断裂作用下动力响应分析, 获取具有普适性的μD.

2 有限元动力计算与结果分析

2.1 有限元动力计算

使用有限元软件ANSYS/LS-DYNA建立第1节构建的100 m跨径拱梁组合标准桥, 有限元模型示意见图2. 其中, Beam161单元模拟拱梁组合桥的拱肋、 横梁、 系梁、 横撑, 利用双单元法来模拟钢管混凝土[16]. 吊杆、 结构质量分别采用Link167、 Mass166单元模拟[8]. 各构件的弹性模量和密度根据《公路钢筋混凝土及预应力混凝土桥涵设计规范 (JTG D62—2004)》[17]规定取值, 边界设置为两端简支.

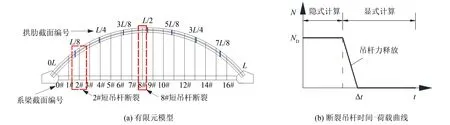
图2 ANSYS/LS-DYNA有限元动力分析模拟 Fig.2 Finite element dynamic analysis simulation in ANSYS/LS-DYNA

吊杆断裂动力过程模拟主要分为两个步骤[8]:

1) 分析拱梁组合桥在吊杆断裂前的受力状态, 得到吊杆断裂前的受力状态;

2) 如图1所示, 删除断裂吊杆单元, 并在断裂位置分别添加一对大小相等、 方向相反并随时间变化的荷载ND, 见图2(b), 模拟吊杆断裂的动力过程. 现有研究[6]建议可以偏保守地按桥梁剩余结构百分之一的周期来计算吊杆断裂的时间Δt.

在进行考虑吊杆断裂过程的拱桥动力分析中, 合理的阻尼设置可以提高计算精度. 选取瑞利阻尼作为拱梁组合桥的黏性阻尼计算方法[6]. 瑞利阻尼假设阻尼矩阵(C)为质量矩阵(M)和刚度矩阵(K)的组合. 质量矩阵系数(α)和刚度矩阵系数(β)由下式计算.

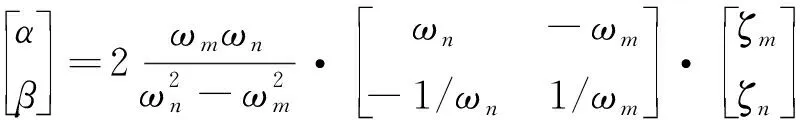
(2)

式中:ωm和ωn分别为第m阶和第n阶固有圆频率;ζm和ζn分别为相应的第m阶和第n阶模态阻尼比.

目前还没有关于结构阻尼的统一计算方法, 结构阻尼比一般根据动力测试的实测结果确定. 文献[8]统计得到15座中、 下承式钢管混凝土拱桥的面内1阶和2阶模态对应的阻尼比介于0.03～0.06. 文献[18]中选择0.03作为100 m拱梁组合桥的总结构阻尼. 由于等效静力法的动力系数(μD)取决于吊杆断裂时结构的动力响应最大值与初始静力响应之比, 结构的最大应力与位移变化均发生在吊杆断裂时刻. 而不同的阻尼设置主要影响断索发生后的结构后续振动曲线的衰减速度, 对吊杆断裂瞬间结构的动力响应变化影响较小. 考虑到结构阻尼会消耗振动体系能量, 进而影响结构的振动, 本研究偏保守地取拱梁组合桥面内1阶和2阶模态对应的阻尼比为0.03, 即ζ1=ζ2=0.03.

2.2 有限元模型正确性验证

建立跨径为20 m的下承式钢管混凝土有限元模型, 对1#和6#吊杆断裂工况进行数值模拟, 并与已有研究中的吊杆断裂缩尺试验模型进行对比验证[8]. 以1#吊杆为例, 断裂时的剩余结构时程曲线如图3所示.

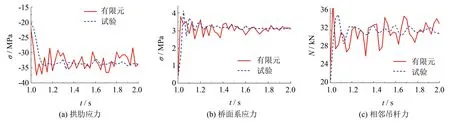
图3 1#短吊杆断裂后时程曲线Fig.3 Time history curves when 1# short suspenders fracture

模型试验与有限元分析得到的吊杆断裂处拱肋、 桥面系的应力时程曲线, 以及与断裂吊杆相邻吊杆的吊杆轴力时程曲线均较为相近. 1#最短吊杆与6#最长吊杆断裂时, 拱肋与桥面系的最大位移和应力, 以及与断裂吊杆相邻吊杆索力最大值见表3. 从表3可以看出, 在长、 短吊杆断裂冲击作用下, 试验与有限元分析结果的最大误差不超过10%. 因此, 本研究考虑拱桥吊杆断裂过程的有限元建模方法具有良好的精度.

表3 长、 短吊杆断裂时试验与有限元结果对比Tab.3 Comparison between test and FE results when long and short suspenders rupture

2.3 吊杆断裂剩余结构受力分析

拱桥吊杆发生断裂主要是因疲劳或环境腐蚀引起, 而拱桥作为对称结构, 累计的损伤也具有对称性质, 横梁上对称的两根吊杆往往是同时断裂[8]. 因此, 下文中开展的吊杆断裂分析均为两根吊杆同时断裂. 拱梁组合桥在拱脚处为固结形式, 温度引起的收缩和徐变突出, 该区域吊杆更容易发生断裂. 其中, 短吊杆最靠近拱脚区域, 但短吊杆初始索力小, 断索引起的剩余结构动力响应不突出, 故选取最靠近短吊杆的次短吊杆进行分析. 长吊杆内力较大且位置特殊, 长吊杆断裂引起的剩余结构动力响应需引起重视. 综上, 选取100 m跨径拱梁组合标准桥的2#短吊杆和8#长吊杆分别进行剩余结构动力响应分析, 2#和8#吊杆位置见图 2(a).

2.3.1吊杆动力响应

吊杆断裂后相邻吊杆的动力响应时程曲线如图4(a). 提取各吊杆在时程曲线中的最不利响应, 断裂前后各剩余吊杆应力对比见图4(b)、 (c). 吊杆断裂后, 断裂吊杆相邻的吊杆应力变化最为明显, 2#短吊杆断裂时1#吊杆的应力由250.01 MPa增加至403.94 MPa, 应力变化率最大为62%; 当8#长吊杆断裂时相邻7#吊杆应力最大为508.07 MPa, 变化率为39%. 当2#短吊杆和8#长吊杆断裂时对相邻吊杆应力影响最大, 且短吊杆比长吊杆对相邻吊杆应力的影响程度更大, 发生断裂后应力增大幅度几乎占到初始索力的62%, 所以应关注吊杆断裂时拱梁组合桥剩余吊杆的受力情况, 防止出现连续吊杆断裂的可能性.

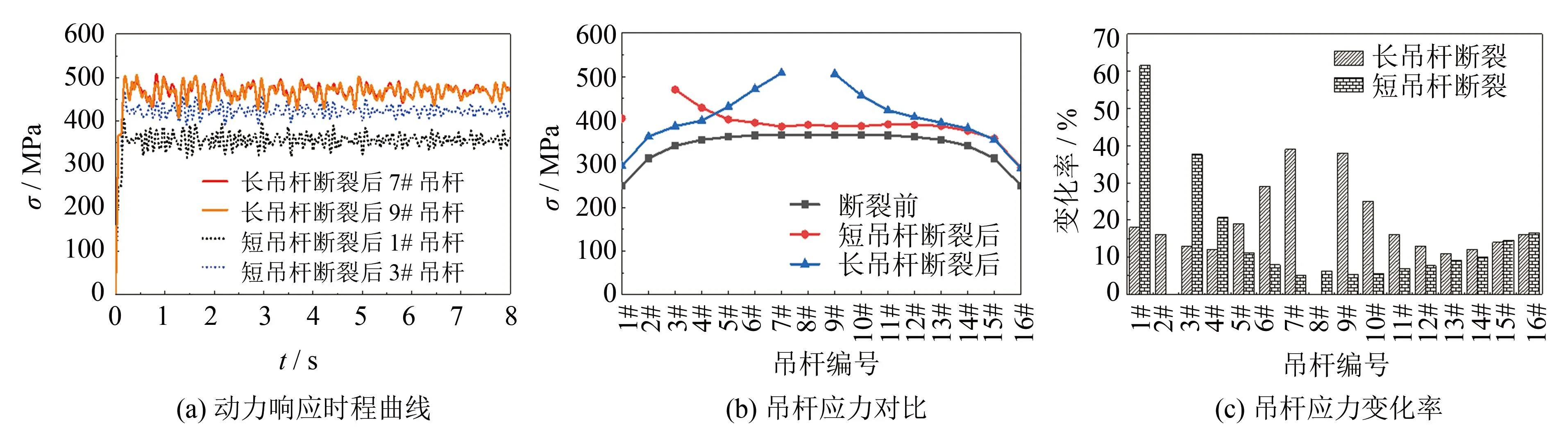
图4 吊杆断裂前后各剩余吊杆应力变化情况Fig.4 Stress change of each remaining suspender before and after suspender fracture

2.3.2系梁动力响应

吊杆断裂后断裂吊杆侧拱脚系梁截面和吊杆断裂处系梁截面动力响应时程曲线如图5(a). 提取系梁各截面在时程曲线中的最不利响应, 吊杆断裂前后系梁各截面应力对比见图5(b)、 (c), 断裂吊杆侧拱脚系梁截面和吊杆断裂临近系梁截面应力变化较为明显. 其中吊杆处系梁截面编号为1#～16#, 0#和17#为两端拱脚系梁截面. 2#短吊杆断裂时对2#系梁截面应力的影响远大于其他截面, 应力增幅为3.60 MPa, 变化率为26%. 8#长吊杆断裂时对8#系梁截面应力的影响远大于其他截面, 应力增幅为5.93 MPa, 应力变化率为42%. 断裂吊杆所对应系梁截面为最不利截面, 且长吊杆比短吊杆对系梁截面的影响程度更大.

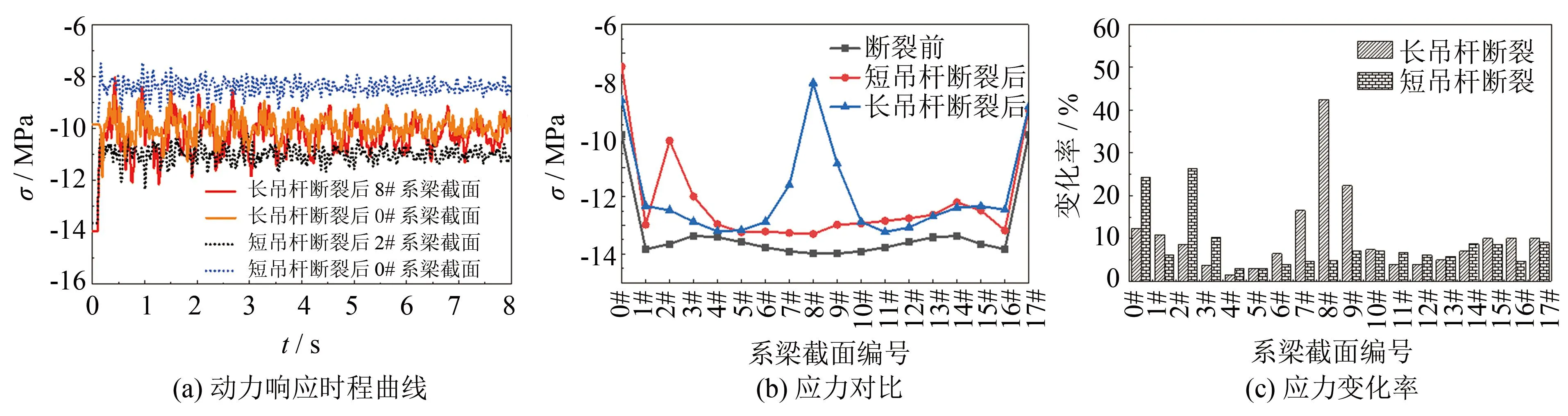
图5 吊杆断裂前后系梁截面应力变化情况Fig.5 Stress change of tie-beam section before and after suspender fracture

2.3.3拱肋动力响应

吊杆断裂后拱肋最大应力截面动力响应时程曲线如图6(a). 提取拱肋各截面在时程曲线中的最不利响应, 吊杆断裂前后拱肋各截面应力对比见图6(b)、 (c), 从1#吊杆侧拱脚到16#侧拱脚截面分别记为0L～L. 从图中可见, 2#短吊杆断裂时对0L和L/8拱肋截面应力的影响远大于其他截面, 0L和L/8拱肋截面应力增幅分别为-18.74和-20.47 MPa, 变化率分别为22%和44%. 8#长吊杆断裂时对L/2拱肋截面应力的影响远大于其他截面;L/2拱肋截面应力增幅为-25.08 MPa, 应力变化率为57%. 在吊杆断裂作用下, 长、 短吊杆断裂后拱肋的最大压应力分别为103.37和92.53 MPa, 对于采用Q345钢的拱肋, 其承载能力仍然具有一定的安全度, 故吊杆断裂对拱肋的影响相对较小.

3 拱梁组合桥动力系数取值分析

3.1 跨径100 m拱梁组合标准桥

已有研究结果[8, 17]与文中2.3节均表明, 短吊杆断裂对剩余吊杆的动力响应影响较大, 长吊杆断裂对系梁的动力响应影响较大, 二者对拱肋的影响均相对较小. 因此, 在分析动力系数μD时, 需分别考虑短吊杆和长吊杆断裂的情况. 吊杆断裂时, 剩余吊杆和系梁的最不利位置分别位于相邻吊杆和断裂吊杆所对应的系梁截面. 以100 m跨径标准桥为例, 讨论在吊杆断裂情况下使用等效静力计算法的动力系数取值.

图7(a)为短吊杆断裂时, 拱梁组合桥剩余吊杆和系梁截面的最不利位置应力比(R,R=等效静力法计算结果/动力计算结果), 吊杆和系梁的动力系数分别为0.583和0.719. 图7(b)为长吊杆断裂时的应力比, 其中吊杆、 系梁的动力系数分别为0.405和0.582. 等效静力计算时, 通常以各构件最大动力系数作为全桥动力系数, 只要保证最不利位置的等效静力计算结果与动力分析结果相符, 其他受力较小的截面的安全性能也能得到保证, 从而就能保证整座拱梁组合桥的安全性. 因此, 取0.719和0.582分别作为短吊杆和长吊杆断裂时的动力系数.

图7 吊杆断裂时跨径100 m拱梁组合标准桥应力比Fig.7 Stress ratio of the 100 m standard arch-girder combined bridge under the suspender fracture

当动力系数为0.719时, 等效静力法、 动力计算法和不考虑吊杆断裂作用的静力法计算结果的比较如图8所示. 等效静力法求得的剩余吊杆和系梁截面应力变化趋势与动力分析结果一致, 相应内力最大值与动力分析结果基本一致, 等效静力法与动力分析的计算结果较为精确. 相比之下, 静力法没有考虑吊杆断裂的冲击效应, 求得的内力均小于动力分析结果.

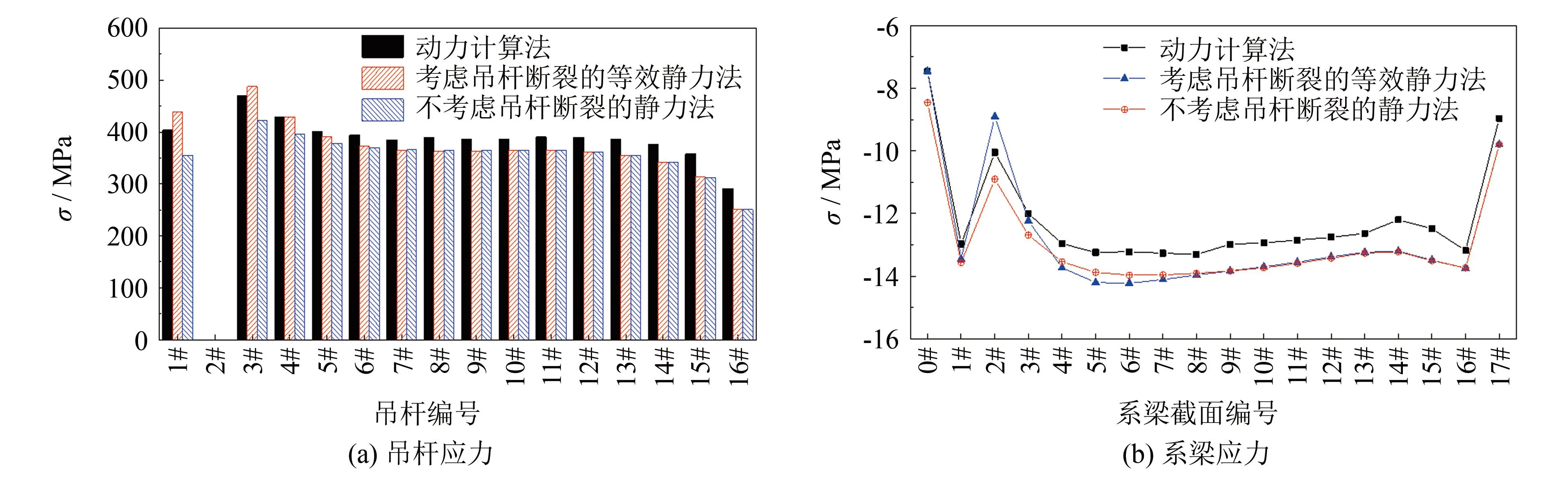
图8 短吊杆断裂不同计算方法对比(μD=0.719)Fig.8 Comparison of different calculation methods under the short suspender fracture(μD =0.719)

当动力系数为0.582时, 3种算法的比较如图9所示. 等效静力法求得的剩余吊杆和系梁截面应力变化趋势与动力分析结果一致, 相应内力最大值与动力分析结果基本一致, 不考虑吊杆断裂的静力法求得的内力均小于动力分析结果.

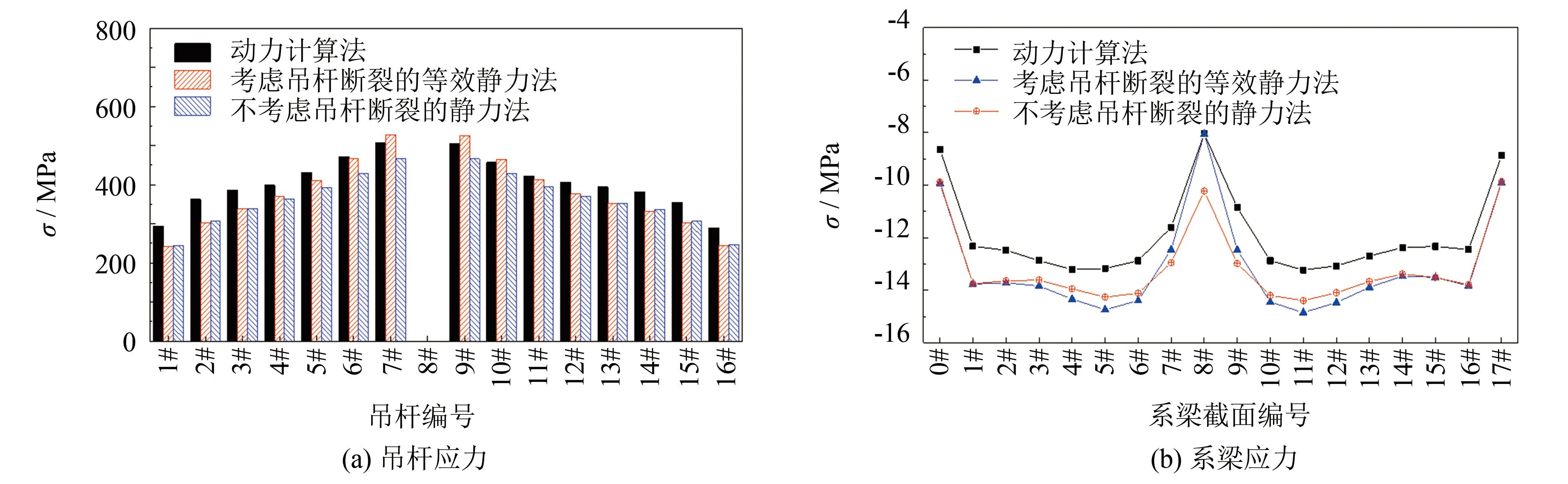
图9 长吊杆断裂不同计算方法应力比较(μD=0.582)Fig.9 Stress comparison of different calculation methods under the long suspender fracture(μD =0.582)

3.2 不同跨径的拱梁组合标准桥

采用上节同样分析方法得到不同跨径拱梁组合标准桥的动力系数, 见图10.

图10 吊杆断裂时不同跨径拱梁组合桥动力系数Fig.10 Amplification coefficient varies with the span under the suspender fracture

图10(a)为短吊杆断裂的情况, 不同跨径拱梁组合标准桥动力系数为0.683～0.788, 动力系数与跨径之间没有明显的规律. 因此, 建议偏安全地取动力系数μD=0.8. 长吊杆断裂时, 不同跨径拱梁组合标准桥动力系数如图10(b). 不同跨径拱梁组合标准桥动力系数为0.510～0.812, 并且随着跨径的增大, 动力系数呈减小的趋势. 构造线性方程μD= -0.005L+1.125, 该线性函数求得的动力系数均大于同跨径剩余吊杆和系梁的动力系数, 可将长吊杆断裂时的动力系数包络. 因此, 建议根据跨径按公式μD= -0.005L+1.125,(50 m≤L≤120 m)取值. 综合长、 短吊杆断裂工况的动力系数, 跨径介于50～120 m的拱梁组合桥动力系数计算公式为

(3)

4 结语

1) 对98座拱梁组合桥关键参数进行统计分析, 构建了跨径为50、 60、 …、 120 m的拱梁组合标准桥, 并依据相关规范规定, 采用有限元软件MIDAS CIVIL对各个跨径拱梁组合标准桥进行了验算, 验算结果满足要求.

2) 采用有限元软件ANSYS/LS-DYNA分析100 m跨径拱梁组合标准桥在吊杆断裂作用下剩余结构动力响应. 结果表明: 长、 短吊杆断裂, 对剩余吊杆与系梁的影响较大, 对拱肋的影响较小. 且短吊杆比长吊杆对剩余吊杆应力的影响程度更大, 发生断裂后应力增大幅度可达初始索力的62%; 长吊杆比短吊杆对系梁的动力响应影响更大, 最大应力变化率为42%.

3) 在拱梁组合桥中采用动力系数的方式考虑吊杆断裂产生的冲击作用, 建立一种能够考虑吊杆断裂作用的拱梁组合桥等效静力计算法. 通过对8种不同跨径拱梁组合标准桥的静、 动力响应分析提出拱梁组合桥等效静力计算法的动力系数计算公式. 当短吊杆断裂时, 动力系数可偏安全地取μD为0.8; 长吊杆断裂动力系数根据跨径按公式取值.