改进BARINEL算法的网络时延故障诊断方法

陈莉琳

(福建省数字福建云计算运营有限公司, 福建 福州 350100)

0 引言

为了保证网络系统能够正常运行, 需要对复杂的网络系统进行监测和故障识别, 并对网络故障进行诊断和定位[1]. 在许多网络系统中, 某些软故障难以检测, 如造成查询的延迟响应, 可能是服务器过载问题, 也可能是网络连接问题, 亦或两者原因都有. 因此, 网络延迟故障诊断是一个值得研究的问题.

近年来, 基于数据的故障检测方法取得了较好进展. 尚志信等[2]采用粗集技术进行网络失效分析, 然后利用经过处理的规则对神经网络进行训练. Kim等[3-4]采用LSTM识别网络异常. 蒋家驹等[5]采用机器学习对现网运行数据进行实时监测, 发现故障隐患. 朱晓荣等[6]采用GAN进行无线异构网络故障检测与诊断. 陈红红等[7]采用改进极限学习机方法实现无线传感器网络故障检测. 上述方法的优点是通用性强, 但缺乏足够的标记数据集[8]. 同时, 也有不少研究将图论和概率模型应用于网络故障诊断领域[9-10]. BARINEL算法[11]是一种复杂度较低的基于模型诊断技术, 能够解决多故障程序诊断问题, 但计算过程较为复杂[12]. 文献[13]提出改进的基于频谱的错误定位方法, 采用STACCATO算法[14]生成故障候选集. 综上分析, 已有基于数据分析的研究中, 存在模式识别算法的学习周期长、 需要训练数据量大、 适用性弱等问题, 需要进一步优化故障检测模型, 提升算法模型的网络故障检测能力.

基于此, 本研究提出一种基于模糊逻辑的改进BARINEL算法来进行网络延迟故障诊断方法, 主要研究工作包括: 1) 针对数据的预处理, 提出一种正态分布延迟注入的数据预处理方法, 能够较好模拟网络系统的延迟故障, 解决待分析故障数据集的有效处理. 2) 基于STACCATO算法, 提出一种启发式最小命中集搜索算法. 通过启发式函数和相似性系数计算组件的集合排序, 并对集合进行截断计算, 更快计算得到最小命中集. 3) 提出基于模糊理论拓展的BARINEL算法, 结合误差诊断方法与贝叶斯模型, 有效得到故障诊断候选者及其故障概率, 提高网络延时故障诊断能力.

1 背景知识

1.1 基本符号和变量

为了方便描述相关技术方法及算法, 现将一些基础性符号和变量描述如下, 见表1.

表1 符号和变量Tab.1 Consistent and variable

1.2 最小命中集

本研究中的最小命中集, 是指一个最优的故障诊断候选集合. 具体地, 将最小命中集的描述如下:

设S是N个非空的集合,S={s1,s2, …,sN}.S每个子集si∈S是一个元素的有限集合, 本研究中即故障节点组件.其中每一个子集为一个数字集, 取值范围为j∈{1, 2, …,M}表示.S的最小命题集则是一个集合满足∀si∈S,si∩d≠Ø∧∃d′⊂d:si:∩d′=Ø.S的每个成员都至少有一个d的分量作为成员, 并且d的任何子集都不是命中集.S可能有多个最小命中集, 这就构成了一个最小命中集的集合D={d1,d2, …,dk, …,d|D|}.

本研究中, 集合S被编码为一个N×M的矩阵A.若元素j是集合i的成员, 则元素aij等于1, 否则等于0.对于j≤M, 行Ai*表示一个组件是否是集合i的成员, 而A*j表示组件j是哪个集合的成员.例如一个节点数M=3的集合S={{1, 3}, {2, 3}}, 集合内包括两个小集合,S编码成的矩阵A如表2所示.

表2 S对应的矩阵ATab.2 Matrix A corresponding to S

计算S的最小命中集集合D的一个方法是通过所有可能的组件组合来检查它是否是一个命中集, 如果是命中集, 检查它是否是一个最小的集合, 即不被其他任何更低基数的集合所包含.其中一个集合dk的基数是指集合中的元素数量, 表示为|dk|.

1.3 模糊逻辑

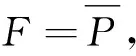
(1)

在模拟逻辑中, 同样假设延迟高于1 s为不正常, 同时假设延迟低于0.5 s为正常, 延迟时间在0.5～1 s表示一种特殊的错误类型. 考虑在这两个阈值之间遵循一个线性模式, 代表这种特殊类型错误的模糊失败级可以定义如下, 其中tr为响应时间,e(tr)表示节点错误类型,μF为隶属函数.即

(2)

1.4 STACCATO算法

使用基于频谱的故障定位(spectrum-based fault localization, SFL), 利用启发式函数计算搜索最小命中集. SFL是一种低成本、 基于统计学的技术, 是能够按概率大小排序故障候选项的良好预测器[16].

在SFL方法计算中, 需要将由集合S编码的矩阵A表示故障诊断选项集合, 为表示频谱矩阵与误差向量的关系, 将其扩展为(A,e), 其中e是一个二进制列,Ai*对应于有异常的系统行为则e=1, 而正常的系统行为则e=0.在STACCATO算法中, 相似性系数采用Ochiai系数[17], 定义为

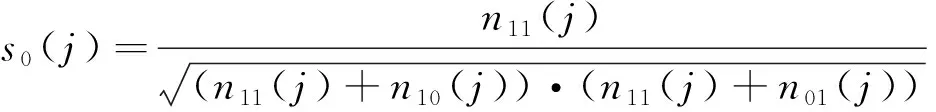
(3)

其中

npq(j)=|{i|aij=p∧ei=q|}|

(4)

相似性系数指的是使用n11(j)的元素, 并使用n10(j)和n01(j)除去n11(j)已有的元素和合集.相似性系数提供了一种产生良好诊断精度的集合排序, 排序越高, 对应的集合存在问题的概率越大.

2 基于启发式函数的最小命中集计算

最小命中集的计算效率会对整个问题的求解时间产生很大影响. 这里, 给出启发式函数H(j), 即

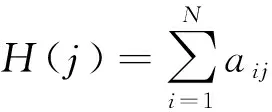
(5)

将函数应用于节1.1的例子, 则H(1)=1,H(2)=1,H(3)=2得到的排名为<3, 1, 2>, 这个排名被用来指导搜索. 从成分3开始, 它参与了两个集合, 因此{3}是一个最小基数的最小命中集. 排名的第二位是成分1, 它没有参与所有的集合, 与那些除了已经被1所覆盖的集合之外的所有集合中涉及到的成分结合起来, 于是可以找到{1, 2}作为第二个最小命中集.

根据上述的分析, 设计了最小命中集算法, 快速计算并获得故障诊断中涉及的相关节点数据. 在N个候选集, 每个有M个候选节点中, 算法得到最小命中集C. 算法如下.

算法1 基于启发式函数的最小命中集算法输入: 矩阵(A, e), 元素数 M, 修剪参数λ, 截断参数 L1. 使用启发式函数计算故障节点的排名2. for 所有组件 do3. 删除所有故障集合共有的异常节点4. whileD≤L do5. 排名前几位的节点, 从矩阵中删除节点的列以及它参与的所有冲突集6. 用 STACCATO算法处理新矩阵7. 组合返回的集合与节点8. 验证是否为最小命中集9. end while输出: 最小命中集D

求解最小命中集问题是一个NP-hard问题, 假设每个候选集有M个候选节点时, 暴力求解的时间复杂度为O(2×M).所提出的启发式函数的最小命中集算法能够将时间复杂度缩减为O(C×M×(N+logM)), 减低了模型求解最小命中集的时间.

3 故障诊断与定位方法

3.1 故障诊断算法

本研究对BARINEL算法使用模糊逻辑进行扩展, 主要区别在于以下计算方法, 即

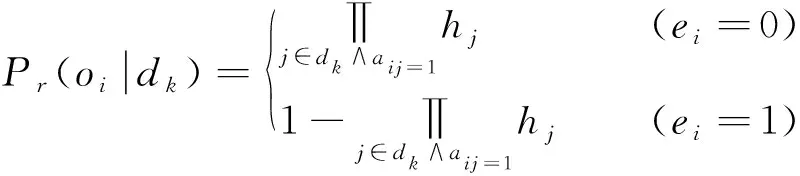
(6)

(7)

分析式(6), 看出该公式只能区分通过的测试和失败的测试, 而式(7)则可以处理软故障, 例如延迟故障等. 当试图优化组件的“健康”[17]时, 可以使用这些方程作为优化问题的一部分, 此处的“健康”, 主要区别于故障的组件, 状态为正常工作、 没有受到故障影响的组件. 在网络故障中, 清晰逻辑中节点只有为正常和失败两种, 但在实际的网络延迟故障中, 需要描述不同故障状态. 故障诊断算法如算法2所示.

算法2 改进BARINEL 算法的故障诊断输入: 频谱矩阵A和误差向量e1. γ←e2. D←STACCATO((A, e))计算最小命中集3. for all dk∈D do4. exp r←GENERATEPR((A, e), dk)5. i←06. Pr[dk]i←07. repeat8. i←i+19. for all j∈dk do10. gj←gj+γ·▽exp r(gj)11. end for12. Pr[dk]i-←EVALUATE(exp r, ∀j∈dkgj)13. untilPr[dk]i-1-Pr[dk]i≤∂14. end for15. return SORT(D, Pr)16. 输出: 诊断报告D

BARINEL的概率推理算法完成了对候选诊断的鉴别, 给定N个候选诊断集的前提下, BARINEL在诊断鉴别过程的时间复杂度分别为O(N).

3.2 故障定位算法

找出故障节点的最小命中集之后, 提出基于贝叶斯模型的故障定位方法, 候选概率计算方法BARINEL算法.

算法3 基于贝叶斯模型的故障定位算法输入: 预处理后的路径节点数据1. i=02. while i<0:3. 选择随机路径, 生成光谱矩阵4. 产生误差向量5. 使用STACCATO算法生成启发式最小命中集6. 用模糊逻辑扩展的BARINEL计算故障概率, 对故障节点诊断排序7. 用清晰逻辑对故障诊断进行排序8. 计算和打印平均浪费努力输出: 故障节点集合故障概率, 平均浪费的代价

具体地, BARINEL算法计算返回在逻辑上与观察结果一致的诊断候选项dk, 并基于贝叶斯方法计算诊断候选项的概率Pr(dk), 实现候选项的有效排名.为了计算dk是真实诊断的后验概率, 给定观察值oi(它指的是测试的覆盖率和错误信息), 具体计算如下式.

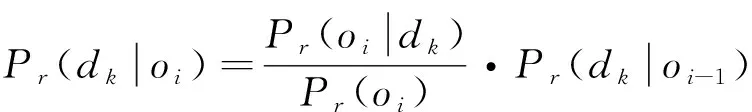
(8)

4 实验结果与分析

4.1 数据集及预处理

实验数据集cycle-aslinks.l7.t1.c0075 32.20190629, 来源于加州大学圣地亚哥超级计算机中心, 包含对Scramper traceroute跟踪的自治系统(AS)的相关数据. 该数据集适用于网络自治系统(AS)的拓扑结构分析及故障诊断等领域.

实验抽取2019-06-29 上午07:15～2019-06-30 下午03:46之间记录的数据. 对数据集进行解析, 提取自治系统链接和组件, 通过python脚本networkx模块编码随机选择记录文件的2 000条边, 然后, 提取该子图中最大的连通分量, 剩下1 520个节点和1 721条边. 同时按以下规则向组件(即路径中节点)中注入延迟故障.

1) 根据分布μ=0.5、σ=0.62来生成延迟, 如图1所示.

图1 延迟注入动态分配图Fig.1 Dynamic allocation diagram of delayed injection

2) 将低于50 ms的值设置为0 ms, 并将大于200 ms的值设置为200 ms.

3) 将50到200 ms范围内的延迟注入到5%的组件中.

通过向组件中注入延迟的方法来模拟网络中的故障. 在实验产生的子图的节点中, 有67个被注入了延迟. 延迟故障可视化表示如图2, 图中尺寸和颜色强度代表延迟, 一个组件的延迟越多, 它的红色就越强烈, 大小就越大; 绿色节点的延迟低于错误阈值(0.2 ms).

4.2 实验验证

分别使用模糊逻辑扩展的BARINEL算法(以下简称为Fuzzy BARINEL)和清晰逻辑的BARINEL算法对网络故障进行诊断实验. 首先, 创建生成频谱矩阵和误差向量的数据, 生成了包含15～30个随机节点(节点间具有连接性约束)的子数据集; 然后, 在这些节点中随机选择路径, 限制路径不能在一条路径中包含所有异常节点; 最后, 将每条路径作为频谱矩阵和误差向量的行, 频谱矩阵列出路径中的节点对于创建频谱矩阵和误差向量要求: 即如果分量(列)j含在路径(行)i中, 则频谱矩阵中的条目为1, 否则为0; 误差向量由每条路径的累积延迟组成.

对于每个子数据集, 选择每个测试次数(10、 20、 30、 50、 100), 随机选择测试(路径)50次, 以计算每种方法的平均浪费代价. 创建包含随机节点的子数据集. 实验中有22个节点被选择为故障候选集, 其中4个节点存在异常延迟. 节点是枚举的, 都代表一个真实的节点ID. 表3为其中一条路径的节点和延迟的信息, 计算得到有延迟故障的异常节点, 其余节点的延迟为0.

表3 路径节点延迟信息Tab.3 Path node delay information

随机选择30条路径, 形成频谱矩阵与误差向量, 并用表格进行记录, 选取部分路径的频谱矩阵和误差向量, 见表4. 最左列表示路径, 第1行表示路径上的节点.

表4 频谱矩阵Tab.4 Spectrum matrix

接着, 用误差向量表示的模糊错误为累积延迟, 将它映射到[0.2, 1.0], 0表示路径中没有超过阈值的延迟, 0.2是代表延迟阈值的最低误差, 1.0是最大累积延迟. 计算得到的误差向量结果如表5所示.

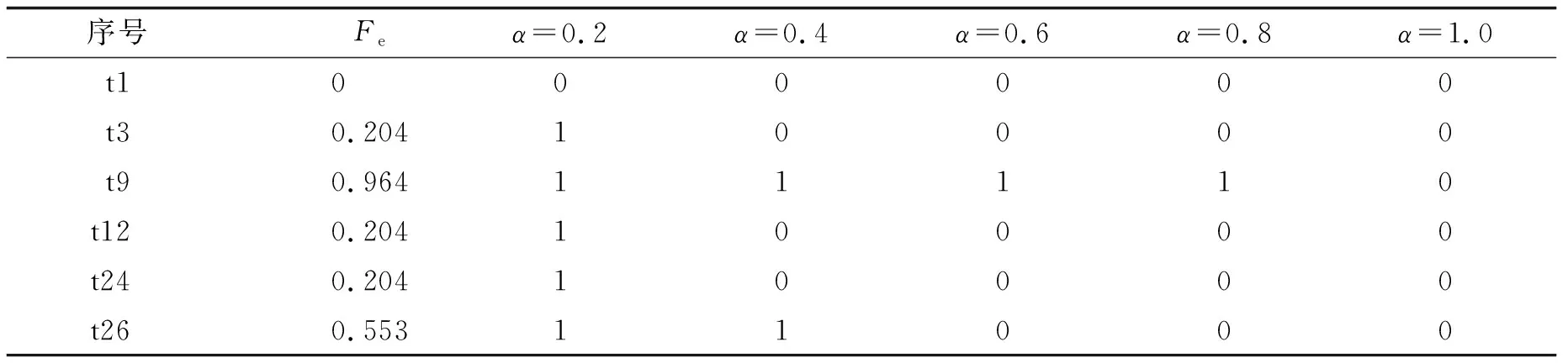
表5 误差向量结果Tab.5 Result of Error vector

表5中:Fe表示为标准化后的累积延迟;α表示所设置的清晰逻辑的阈值. 为了对比模糊逻辑与不同阈值下的清晰逻辑的诊断结果, 阈值分别设置为0.2、 0.4、 0.6、 0.8和1.0, 当标准化后的误差向量大于等于阈值返回1, 小于阈值时则返回0.

将频谱矩阵和误差向量输入到BARINEL代码中, 用模糊逻辑扩展BARINEL计算出诊断故障节点最小命中集故障概率结果如表6. 表中:F表示为累积延迟, 括号内为可能的故障集, 冒号后为故障概率.

表6 节点集合故障概率Tab.6 Node fault set probability

分析表6中的结果, 通过使用Fuzzy BARINEL, 都为异常节点的诊断(10, 13, 16, 20), 排名第一, 概率为0.504 4. 使用阈值为0.2和0.4的清晰BARINEL给出了相同的结果, 概率分别为0.500 0和0.512 2. Fuzzy BARINEL能够有效地诊断出可能的异常节点, 得到诊断候选集.

4.3 计算性能对比实验

为了验证清晰逻辑和Fuzzy BARINEL算法的计算性能, 开展了相关对比实验.

诊断性能是用诊断性能指标W来衡量的, 该变量为50次随机实验中判断错误的节点数量平均值, 称为平均浪费代价, 该值计算为W=N/50,N为判断错误的节点数量, 若W=0, 表示没有浪费额外的代价去测试其他故障集合判断故障与否.计算用清晰逻辑和模糊逻辑两种方法在不同路径数量下找到正确诊断平均浪费的代价W, 在5个子数据集的每个子数据集中随机选择50次以计算平均值. 对比结果如表7所示.

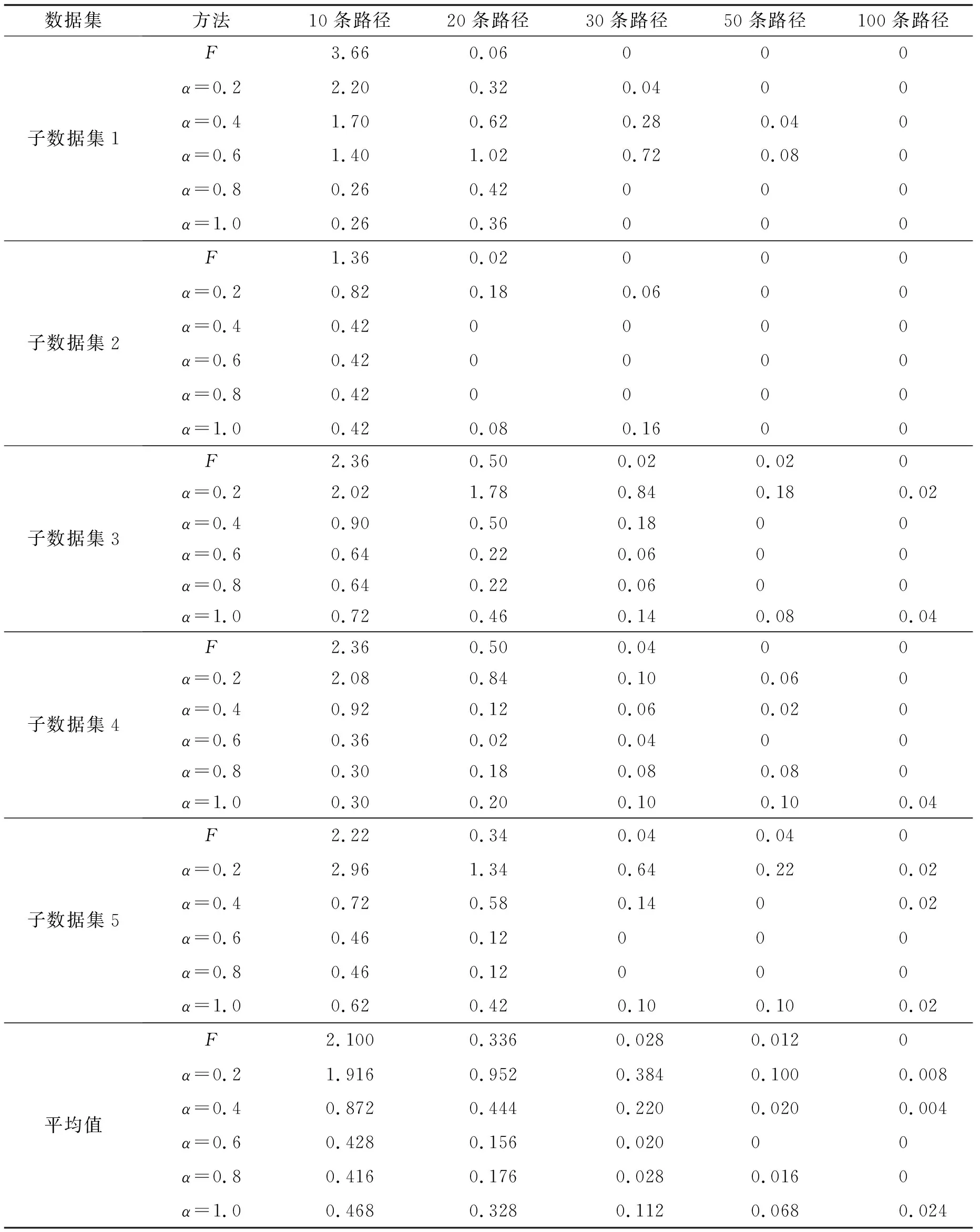
表7 找到正确诊断的平均浪费代价对比Tab.7 Average wasted cost of finding the right diagnosis

进一步将上述平均浪费代价平均值结果进行可视化对比, 具体如图3所示. 图中的折线对应了模糊逻辑和不同阈值的清晰逻辑的算法在不同路径数量下的浪费代价平均值, 横坐标为路径数量.

图3 平均浪费代价结果Fig.3 Average wasted cost

由图3可知, 当清晰逻辑阈值设置较低时, 故障诊断效果明显低于Fuzzy BARINEL, 如图中α=0.2和α=0.4时, 在诊断10到30条路径上产生了较差的效果.而当设置较高阈值时, 如α=0.8,α=1.0, Fuzzy BARINEL在大多数情况下的表现比清晰逻辑好, 浪费代价更少, 较高的阈值可能会误判测试中异常组件.

5 结语

针对网络延迟故障分析与定位问题, 本研究先采用基于启发式函数的最小命中集算法STACCATO, 利用Ochiai相似性系数组件集合排序, 计算出故障组件的排名截, 有效地计算出最小命中集. 进一步使用Fuzzy BARINEL算法得到正确的故障候选集. 实验表明, 本文提出的算法能够有效诊断出延迟故障链路及故障点, 且具备较高的计算效率.

下一步, 将所提出的Fuzzy BARINEL算法针对多种网络故障识别开展研究, 使得算法具有更好的适应能力.