具有避难所的离散捕食者-食饵系统的动力学行为分析
2023-12-28林思佳陈凤德陈尚铭周起梅
林思佳, 陈凤德, 陈尚铭, 周起梅
(福州大学数学与统计学院, 福建 福州 350108)
0 引言
Leslie-Gower捕食者-食饵模型是近年来数学生态学的研究热点[1-5]. 其中, 食饵具有避难所的Leslie-Gower捕食者-食饵系统得到了许多学者的关注和研究[1, 4-5]. 此外, 考虑到食饵会因被捕食风险而产生恐惧并做出反捕食行为, 进而导致食饵种群密度下降. 食饵因恐惧而做出的反捕食反应被称为恐惧效应. 许多学者在研究捕食者-食饵系统时都考虑了恐惧效应[1, 5-7].
考虑到对于数量很小或者世代不重叠的种群, 物种间的相互作用使用离散模型来描述更为合适. 许多学者对离散的捕食者-食饵系统进行研究[1, 7-8]. 最近, 文献[1]提出如下食饵种群具有恐惧效应和避难所的修正Leslie-Gower离散捕食者-食饵模型为

(1)
其中:x(t)、y(t)分别表示食饵种群和捕食者种群第t代的种群密度;r和μ分别表示食饵种群和捕食者种群的内禀增长率;a和c分别表示食饵种群和捕食者种群由于种内竞争导致的死亡率;k反映了食饵的恐惧程度;b为半饱和常数;m表示食饵中由于有避难所的保护而完全不受捕食的比例, 衡量了避难所的有效性;a、c、b、r、μ、k、m均大于0且为常数, 特别地,m∈(0, 1).
令θ=1-m∈(0, 1), 通过计算可得, 系统(1)总存在边界平衡点E0(0, 0)、E1(r/a, 0)和E2(0,bμ/c).此外, 当θ<θ1时, 系统(1)存在唯一的正平衡点E3(x1,y1), 有
注意到, 文献[1]得到的有关系统(1)各平衡点的局部渐近稳定的条件是不够严格的, 在下一节中将给出具体的详尽分析, 通过严格的证明分析给出各平衡点局部渐近稳定的充分性条件. 并在第3节中通过数值模拟验证结果的可行性.
此外, 一方面, 文献[1]给出了系统(1)在边界平衡点E2处存在翻转分支的充分性条件, 而理论分析表明, 此时系统(1)在E2处并不存在翻转分支.另一方面, 文献[1]对系统(1)在边界平衡点E1处存在的分支现象并未进行说明.因此, 本研究在第2节中对系统(1)在该充分性条件下存在的分支类型进行重新探讨, 证明系统在适当条件下存在跨临界分支.同时进一步给出系统(1)在边界平衡点E1和E2处存在翻转分支的充分性条件.
1 平衡点的局部稳定性
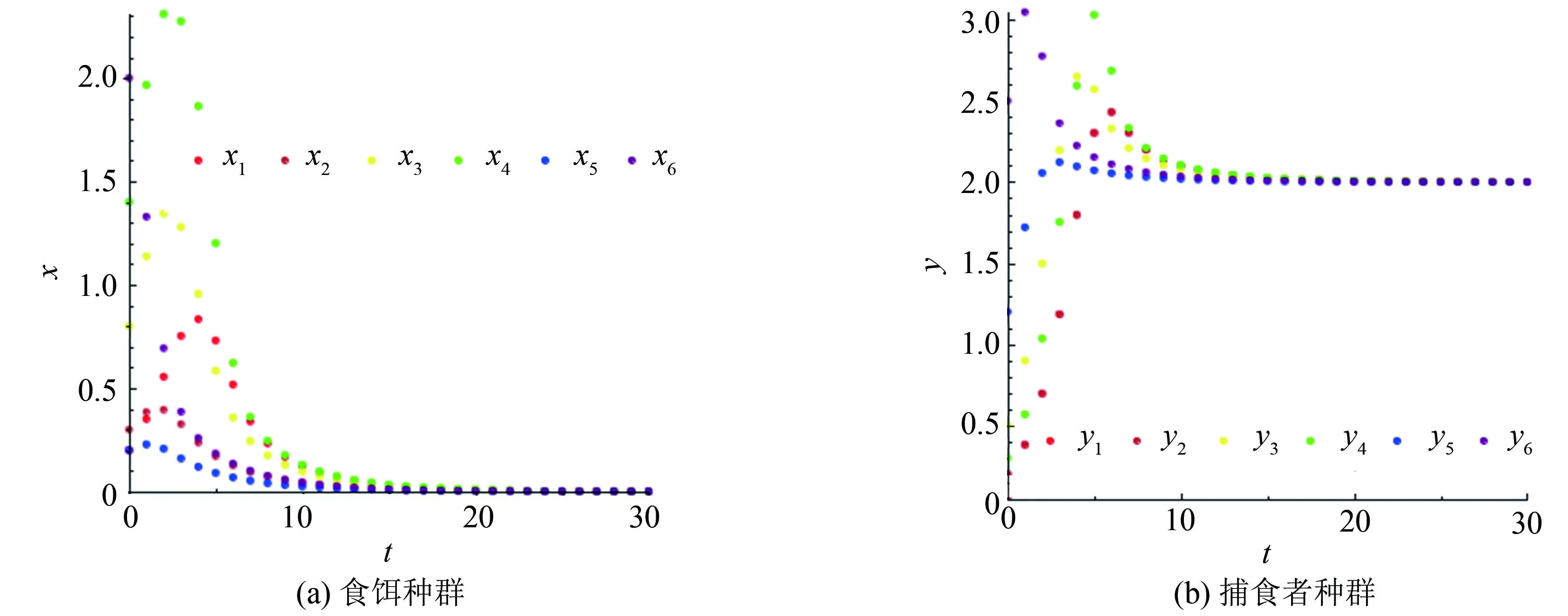
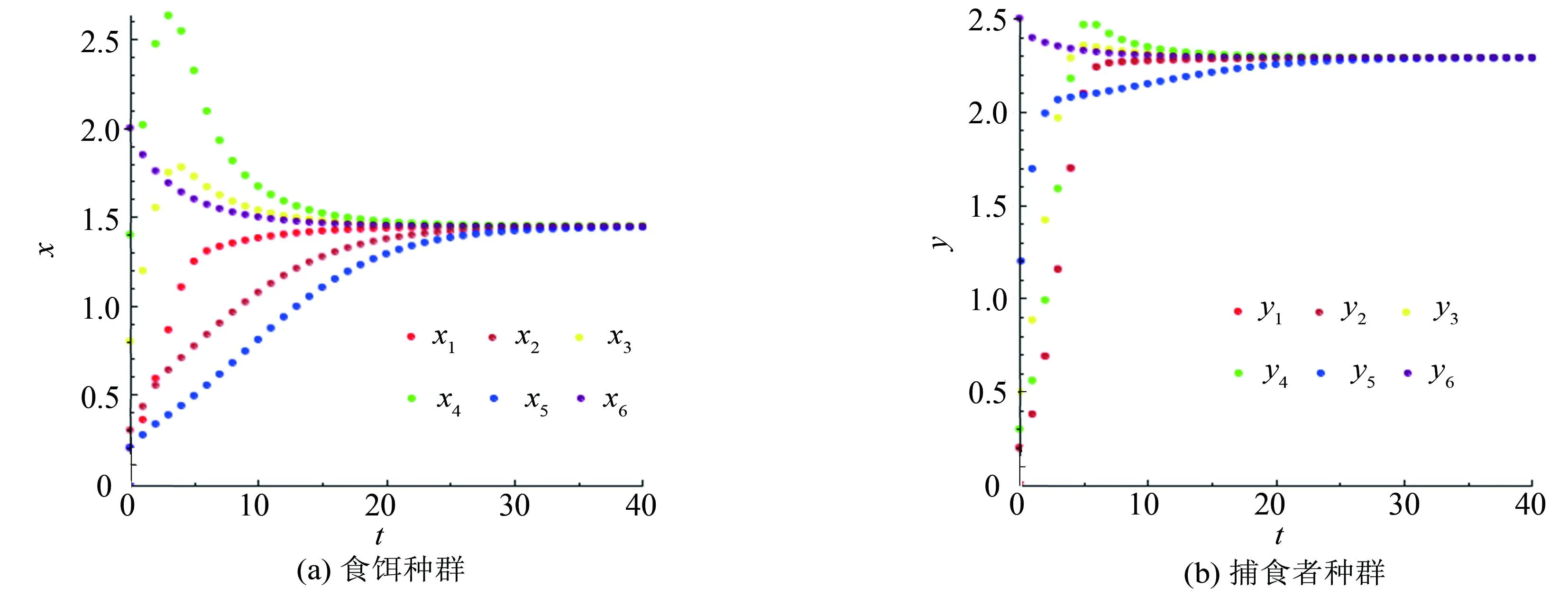
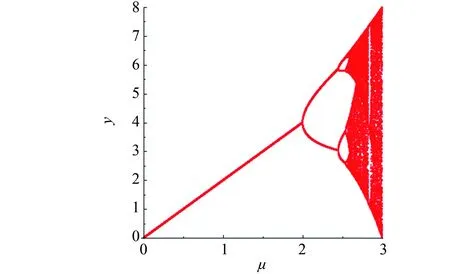
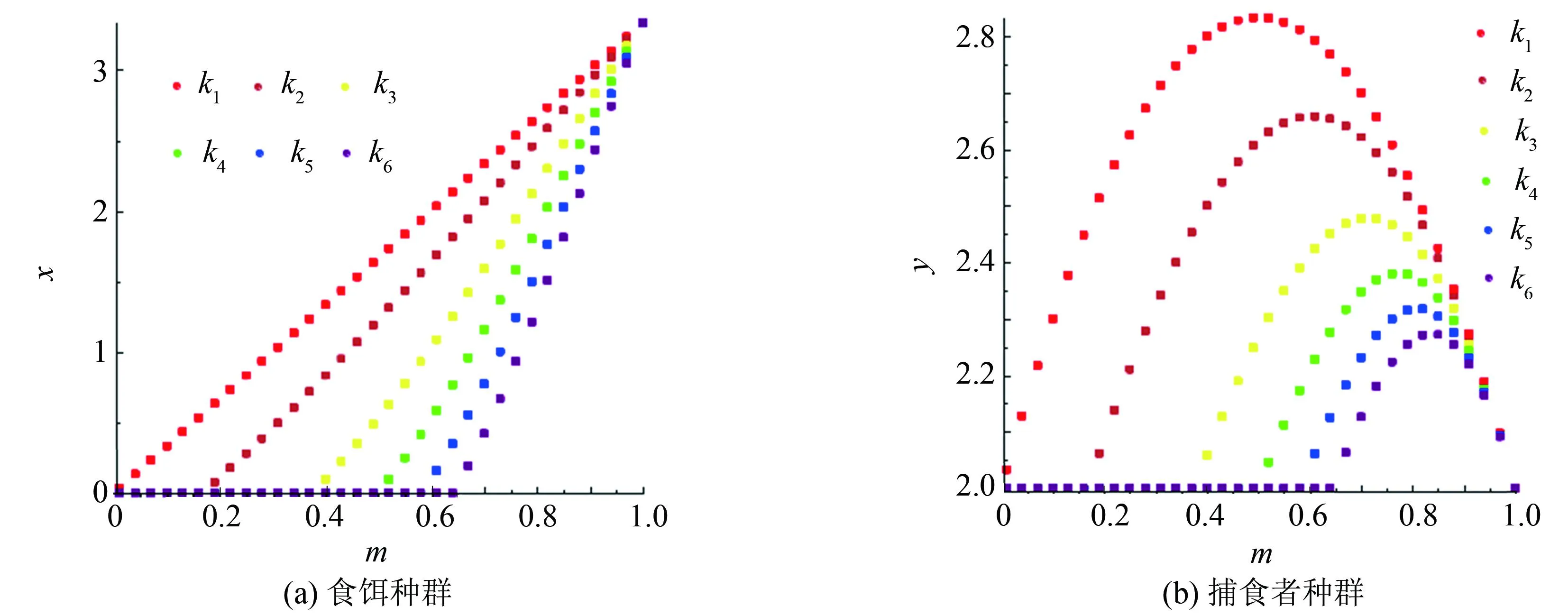
系统(1)在平衡点E(x,y)处雅可比矩阵J(x,y)见文献[1]中式(2.1)和式(2.2).文献[1]中系统(1)在分析相应平衡点的局部稳定性时, 是通过将平衡点处雅可比矩阵的特征值与1进行比较.注意到, 这样对各平衡点的稳定性进行分析是不严谨的.以E2(0,bμ/c)为例, 文献[1]指出当k>(c2r-cμθ)/(bμ2θ):=k*时,E2是稳定的.事实上, 设定系统(1)的各参数值为:k=0.8,a=0.3,b=2,r=1,c=1,μ=2.7,θ=0.3, 取系统(1)的初始条件为(x(0),y(0))=(0.5, 0.3).此时,k*=0.04 图1 食饵灭绝边界平衡点不稳定Fig.1 Prey free equilibrium is unstable 接下来利用文献[8]关于局部稳定性的理论重新分析系统(1)的各平衡点的局部稳定性. 定理1系统(1)始终存在一个边界平衡点E0(0, 0), 且E0是一个源, 是不稳定的. 证明: 系统(1)在E0处的雅可比矩阵J(E0)见文献[1]中式(2.4), 其特征根分别为λ1=1+r,λ2=1+μ.由于r,μ>0, 所以始终有|λ1|>1且|λ2|>1.故由文献[8]得,E0是一个源, 是不稳定的. 定理2系统(1)始终存在一个边界平衡点E1(r/a, 0), 且E1始终是不稳定的: 1) 当r>2时,E1是一个源; 2) 当r<2时,E1是一个鞍点; 3) 当r=2时,E1是一个非双曲的平衡点. 证明: 系统(1)在E1(r/a, 0)处的雅可比矩阵为 则J(E1)的特征值分别为λ1=1-r<1,λ2=1+μ>1.因为μ>0, 则有λ2>1.当r>2时, 有λ1<-1, 即|λ1|>1, 结合λ2>1, 由文献[8]知,E1是一个源.2)~3)类似可证. 定理3系统(1)始终存在一个边界平衡点E2(0,bμ/c), 且有 Ⅰ) 当μ<2且θ1<θ<θ2时,E2是一个汇; Ⅱ) 当μ>2且θ满足θ<θ1或θ>θ2时,E2是一个源; Ⅲ) 当以下条件之一成立时,E2是一个鞍点: ⅰ)μ>2且θ1<θ<θ2; ⅱ)μ<2且θ满足θ<θ1或θ>θ2; Ⅳ) 当θ=θ1或θ=θ2或μ=2时,E2是非双曲平衡点.因此, 当μ<2且θ1<θ<θ2时,E2是局部渐近稳定的, 其他情况下E2都是不稳定的, 有 (2) 证明: 系统(1)在E2处的雅可比矩阵J(E2)见文献[1]中式(2.6), 其特征根分别为 故当θ1<θ<θ2且μ<2时, 有|λ1|<1, |λ2|<1, 由文献[8]知, 此时E2是一个汇.Ⅱ)~Ⅳ)可类似探讨. 定理4在系统(1)的正平衡点E3(x1,y1)存在即θ<θ1的前提下, 进一步, 可得 1) 当P 2) 当下列条件之一成立时,E3是一个源: ①Q≤2且P>Q; ②Q>2且P>max(Q, 2Q-4); 3) 当Q>2且P<2Q-4时,E3是一个鞍点; 4) 当P=2Q-4时,E3是非双曲平衡点.其中θ1在式(2)中已给出, 且 这里 (3) 因此, 当P 证明: 系统(1)在正平衡点E3处的雅可比矩阵为 其中 这里,α,β,γ,η均在式(3)中给出, 由于θ<θ1 故J(E3)的特征方程为F(λ)=λ2+Bλ+C=0, 其中 通过计算可得 当P 文献[1]指出, 当k=(c2r-cμθ)/(bμ2θ):=k*时系统(1)在E2处发生翻转分支, 事实上, 此时J(E2)的特征值分别为λ1=1和λ2=1-μ, 并不满足发生翻转分支的条件.但此时系统(1)在E2处可能发生跨临界分支.接下来利用中心流形定理[9]和分支理论[10]进行讨论. 首先将E2(0,bμ/c)平移到原点, 并在原点处作泰勒展开.令u=x,v=y-bμ/c和w=k-k*, 则系统(1)可化为 (4) 其中 f1(u,v,w)=a1u2+a2uv+a3uw+a4u3+a5u2v+a6uv2+a7u2w+ a8uw2+a9uvw+O((|u|+|v|+|w|)4), g1(u,v,w)=b1u2+b2uv+b3v2+b4u3+b5u2v+b6uv2+O((|u|+|v|+|w|)4). 这里, 有 通过可逆线性变换为 可将式(4)化为 (5) 其中 f2(X,Y,Z)=c1X2+c2XY+c3XZ+c4X3+c5X2Y+c6XY2+c7X2Z+ c8XZ2+c9XYZ+O((|X|+|Y|+|Z|)4), g2(X,Y,Z)=d1X2+d2XY+d3XZ+d4Y2+d5X3+d6X2Y+d7XY2+ d8X2Z+d9XZ2+d10XYZ+O((|X|+|Y|+|Z|)4), 且有 这里,ξ=abc2r-abcμθ+3c2r2θ-4cμrθ2+2μ2θ3,ζ=cr-μθ,α在式(3)中已给出. 由中心流形定理可知, 在Z=0的充分小邻域内, 平衡点(X,Y)=(0, 0)处存在一个系统(5)的中心流形Wc(0)可表示为 Wc(0)={(X,Y,Z)∈R3|Y=h1X2+h2XZ+h3Z2+O((|X|+|Z|)3)}. 其中h1=h2=h3=0.因此, 式(5)限制于中心流形Wc(0)的映射可改写为 F:X→X+m1X2+m2XZ+m3X2Z+m4XZ2+m5X3+O((|X|+|Z|)4). 其中 由于 则可以得到以下定理. 定理6当μ=2且θ≠θ1,θ2时, 系统(1)在边界平衡点E2(0,bμ/c)处经历翻转分支. 定理7当r=2时, 系统(1)在边界平衡点E1(r/a, 0)处经历翻转分支. 证明: 由于这两个定理的证明是类似的, 这里仅给出定理6的详细证明.当μ=2且θ≠θ1,θ2时,J(E2)的特征值满足λ2=-1且λ1≠1, -1, 此时可能发生翻转分支.又系统(1)在E2处的中心流形为x=0, 且限制于中心流形x=0的系统(1) 是一个Logistic模型:y→f(y)=y+y(μ-cy/b), 其非平凡平衡点是y1=bμ/c.当μ在μ=2的充分小邻域内时, 有f′(y1)=1+μ-2cy1/b=-1, 故系统(1)会在边界平衡点E2处发生翻转分支. 例1通过数值模拟研究平衡点E2(0,bμ/c)的局部稳定性. 设定各参数值为:k=0.8,a=0.3,b=2,r=1,c=1,μ=1,θ=0.6, 此时,θ1=0.38且θ2=2.38, 则μ<2且θ1<θ<θ2.由定理3知, 此时E2(0, 2)是局部渐近稳定的, 分别取系统初值(x(0),y(0))为 (x(0),y(0))=(0.2, 0.2), (0.3, 0.9), (0.8, 0.5), (1.4, 0.3), (0.2, 1.2), (2.0, 2.5) (6) 进行数值模拟, 其结果验证了定理3结论的准确性, 如图2所示, 其中(xi,yi)(i=1, 2, …, 6)分别表示系统(1)对应上述初值的解. 图2 食饵灭绝平衡点E2的局部渐近稳定性Fig.2 Local stability of prey free equilibrium E2 例2通过数值模拟研究正平衡点E3(x1,y1)的稳定性. 设定各参数值为k=0.8,a=0.3,b=2,r=1,c=1,μ=1,θ=0.2, 此时,θ1=0.38>θ, 且P=0.17,Q=1.09, 显然有P 图3 正平衡点E3的局部稳定性Fig.3 Local stability of positive equilibrium E3 例3通过数值模拟研究系统在E2处的翻转分支. 分别设定各参数值为:k=0.8,a=0.3,b=2,r=1,c=1,θ=0.2, 同时设定初始条件为(x(0),y(0))=(0.5, 0.3).通过数值模拟可知, 此时食饵种群绝灭, 而捕食者种群由于有其他食物来源, 随着其内禀增长率μ的增大, 经历翻转分支, 由稳定平衡点分岔为稳定两点环、 稳定四点环、 稳定八点环, 最终发生混沌现象, 如图4所示. 图4 系统在E2处的翻转分支图Fig.4 Flip bifurcation diagram of the system at E2 例4通过数值模拟研究避难所对系统的影响. 分别设定系统(1)各参数值为:a=0.3,b=2,r=1,μ=1,c=1, 同时设定初始条件为(x(0),y(0))=(0.5, 0.3).以衡量避难所有效性的参数m为横坐标作图, 分别令恐惧因子为k1=0,k2=0.1,k3=0.3,k4=0.5,k5=0.7,k6=0.9, 进行数值模拟, 如图5所示.由图5(a)可以看出, 当提供的避难所保护较小时, 食饵最终将会绝灭.当m∈(0, 1)不断增大时, 部分食饵由于有了避难所的保护而免受捕食, 食饵种群便不会绝灭, 能稳定生存, 且种群密度也在不断增加.此外, 当食饵因对潜在的被捕食风险产生恐惧时, 只有提供充分的避难所保护, 才能保证食饵种群不会绝灭.且随着恐惧效应的不断增加, 维持食饵种群生存所需提供的避难所保护也随之增大.当避难所保护所有食饵不受捕食时, 不同恐惧效应下的食饵种群密度都达到了相同的峰值. 图5 避难所对系统的影响Fig.5 Impact of the refuge on the system 由图5(b)可以看出, 当m∈(0, 1)且不断增大时, 捕食者种群密度先增大后减少, 也就是说, 对食饵提供一定程度的避难所保护, 对捕食者种群的增长也是有利的. 结合图5(a)可以发现, 当提供的避难所保护维持在一定范围时, 避难所有利于捕食者种群与食饵种群的稳定共存, 同步增长. 此外, 恐惧效应越大, 捕食者种群密度所能达到的峰值越小. 可能的原因是随着恐惧效应的增大, 食饵种群的数量不断减少, 进而引起捕食者种群的减少. 本研究首先分析了系统(1)平衡点的局部稳定性, 给出了保证系统的食饵灭绝边界平衡点, 以及正平衡点局部稳定的充分性条件, 所得结果改进和完善了文献[1]关于该模型的稳定性分析和分支分析的相应结果. 其次, 利用中心流形定理和分支理论, 对文献[1]关于系统(1)在边界平衡点处存在的分支现象进行修正和补充, 系统在食饵灭绝边界平衡点处会经历跨临界分支. 此外, 捕食者种群和食饵种群都会随着其内禀增长率的增大经历翻转分支, 由稳定平衡点分岔为稳定两点环、 稳定四点环、 稳定八点环, 最终发生混沌现象. 最后, 通过数值模拟验证了主要结果的可行性, 同时探讨了避难所对系统的影响. 当提供的避难所保护维持在一定范围时, 避难所可以减少食饵被捕食而灭绝的机会, 从而促进食饵种群和捕食者种群的稳定共存、 同步增长.
1.1 边界平衡点E0(0, 0)的局部稳定性
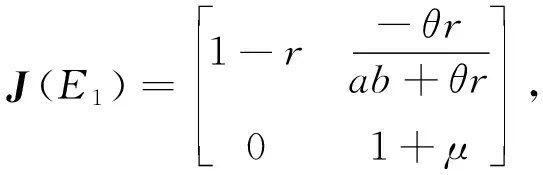

1.2 正平衡点E3(x1, y1)的局部稳定性

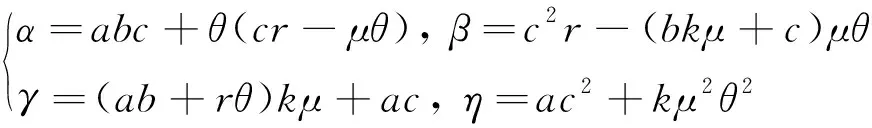

2 分支分析
2.1 边界平衡点E2处的跨临界分支




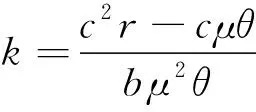
2.2 边界平衡点E1, E2处的翻转分支
3 数值模拟
4 结语
