基于模糊PID的恒功率车削控制方法

夏弋涵，罗敏，张超勇，樊峻杉，李泽亚

（1.湖北汽车工业学院，湖北 十堰 442002；2.华中科技大学 数字制造装备与技术国家重点实验室，湖北 武汉 430000；3.东风设备制造有限公司，湖北 十堰 442000）

数控加工过程与切削三要素（切削速度、进给速度和背吃刀量）密切相关［1］，预先给定的工艺参数常由操作者的先验知识确定。为保证加工过程正常进行，参数选择具有一定的保守性和恒定性。但加工过程受切削深度、工件硬点等因素的影响，具有高度非线性化的特点，恒定且保守的参数不能很好地适应复杂的加工过程，严重影响加工效率，因此数控加工过程自适应控制方法成为了研究热点。目前传统PID 控制等经典算法逐渐被模糊控制等智能算法取代。文献［2］选用模糊控制算法，以功率恒定为约束条件实现自适应控制；文献［3］考虑颤振因素对自适应控制的影响，运用模糊控制规则实现恒功率控制；文献［4］将边缘控制器与二维模糊控制器相结合实现铣削过程的恒功率控制；文献［5］将现场总线与模糊控制结合，以调整模糊控制器比例因子的方式实现自适应控制；文献［6］以主轴电流作为反馈信息，结合主轴负载模型的拟合，通过模糊控制算法实现进给倍率的调整。上述文献均采用模糊控制算法作为核心控制算法，隶属度函数与推理规则恒定不变，随着加工条件的改变，控制效果并不稳定。为此，文中通过模糊控制算法实时调整PID控制器的参数，提高控制过程的自适应性。

1 控制系统

进给速度与主轴功率呈现正相关趋势［7］，背吃刀量增大时需降低进给速度，背吃刀量减小时提升进给速度，以保持主轴功率恒定。

车削过程的控制系统是恒功率闭环控制系统，结构如图1 所示。功率传感器将采集到的主轴功率传输给核心控制器PLC，通过模糊PID算法计算出优化后的进给倍率调整值，并通过8位数字量输出端口传输给CNC 系统中的PMC；然后由CNC 系统控制驱动器下的伺服电机，进而改变进给速度，将主轴功率维持在目标功率的误差范围内，达到自适应控制的目的。

图1 闭环控制系统工作原理图

2 数学模型

以数控系统为FANUC 0i-TD 的CK0628 数控车床为试验对象，选用CCGT09T308-AKH01 菱形铝用刀片以及6061铝棒进行试验。

2.1 模型结构

车削加工系统的过程模型如图2所示，将伺服环节简化为二阶系统［8］：

图2 车削过程模型框图

式中：s为拉氏变换算子；Vf为进给速率，mm·s-¹；u为电枢电压，V；Km为伺服增益，mm·（V·s）-¹；ωn为伺服系统的自然频率，rad·s-¹；ξ为阻尼系数。

文献［9-10］使用切削力模型实现加工过程恒力控制的仿真。与切削力信号相比，功率信号包含的加工过程信息更完整，且在线监测更便捷，成本更低，因此建立基于切削三要素的主轴负载模型。已知主轴负载的通用关系模型为

式中：n为主轴转速，r·min-¹；D为工件直径，mm；Kr为刀具主偏角；f为每齿进给量，mm；a为背吃刀量，mm；K和c为待定系数。

2.2 模型拟合

为保证实验数据的多样性，按照全面实验要求进行三因素三水平实验，设置主轴转速为（500，1000，1500）r·min-¹，背吃刀量为（1，2，3）mm，进给速度为（0.1，0.2，0.3）mm·min-¹，共进行27 组实验。通过NC 程序，控制每组实验参数以设定值持续车削50 mm。考虑到加工材料有硬点、车削过程中有切屑等实验情况，通过上位机以0.5s间隔采集主轴功率，并选取材料去除过程中的数据进行求平均值处理。实验数据如表1所示。

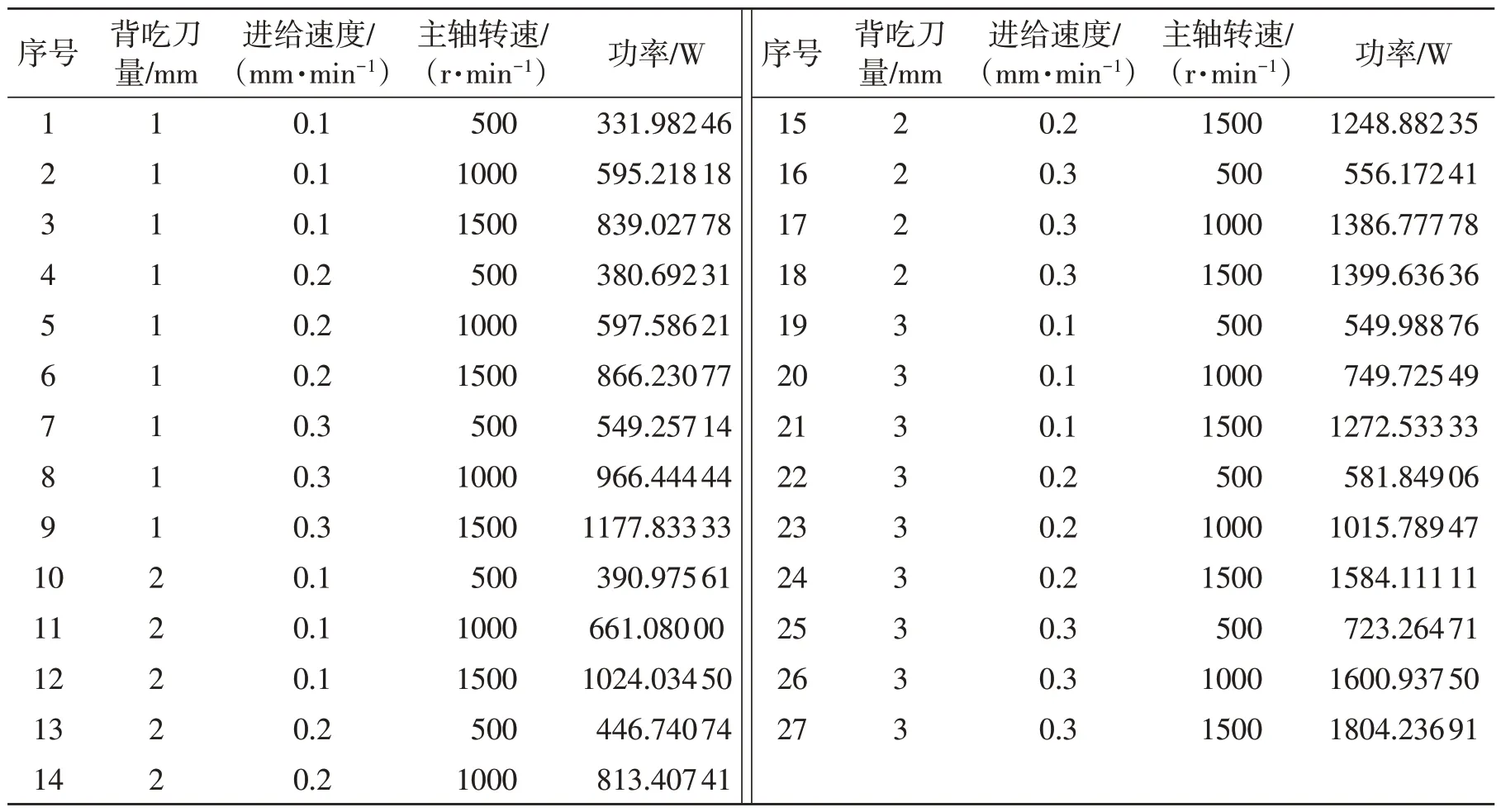
表1 全面实验数据

使用MATLAB 的nlinfit 函数拟合采集到的数据得待定系数K和c。为简化建模过程，根据文献［8］确定伺服机构的参数。车削加工系统模型的各项参数如表2所示。

表2 车削加工系统模型参数

车削过程的主轴负载关系模型为

相应传递函数为

选用均方差（MSE）作为模型的评估标准，MSE为5.9861则表明模型效果相对较好，能有效为后续仿真和实验提供依据。车削加工系统由车床伺服环节、进给速度与每齿进给量转化过程、车削过程组成，因此传递函数为

3 模糊PID控制器

传统PID 控制器的参数（比例系数Kp，积分系数Ki，微分系数Kd）恒定，不适用于日益复杂的车削加工过程，且系统性能稳定性较差，易受扰动影响。模糊PID 控制方法是将目标功率与实时功率比较，得到实时功率误差e，和误差变化率ė一起作为输入，经模糊控制处理，输出PID 控制器3 个参数的调整值（ΔKp、ΔKi、ΔKd），实现对PID 控制的实时参数调节。模糊PID控制过程为闭环控制过程，如图3所示。

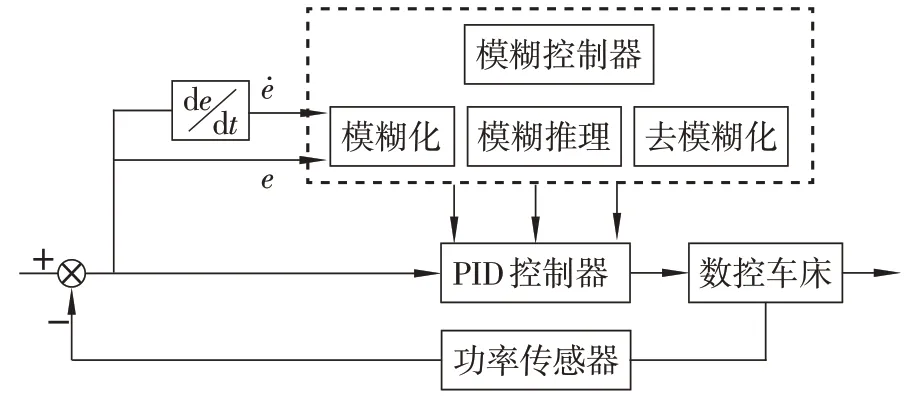
图3 控制过程框图

模糊化阶段主要由论域确定和隶属度函数选择组成。将模糊控制输入、输出量的模糊子集设定为{NB,NM,NS,ZE,PS,PM,PB}，即{负大、负中、负小、零、正小、正中、正大}，论域都确定为（-6，6）。考虑实验设计的灵活性和简便化，选择三角隶属度函数。首先通过量化因子将输入量的物理论域转换为模糊论域，e和ė的量化因子分别为

式中：n为模糊论域的正边界值。接着将处理后的输入值映射到论域的各个区间，然后通过三角隶属度函数确定其相应隶属度。

模糊推理阶段，由e和ė的隶属度计算出的隶属度如表3所示。

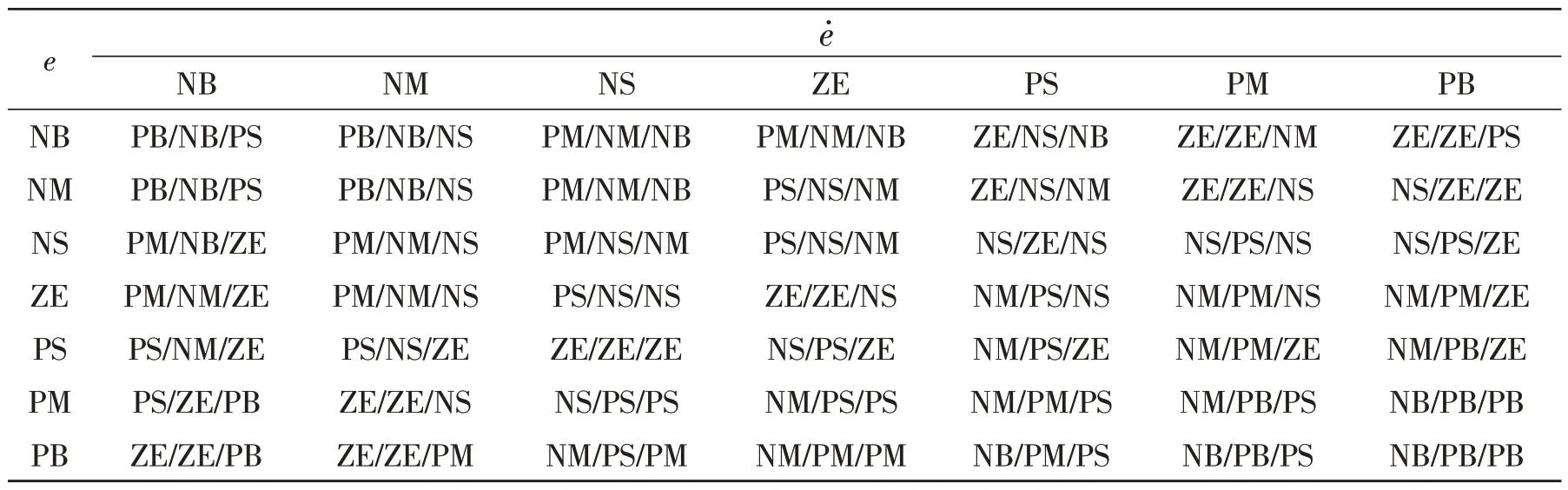
表3 ΔKp、ΔKi、ΔKd模糊推理规则

去模糊化阶段选用重心法去模糊，即算出输出期望并根据区间映射关系得到输出值：

式中：Δafi为规则i的相关值；Hi为规则i的相关成员；k为规则总数。去模糊化后的输出值经比例因子处理后传递给PID 控制器，ΔKp、ΔKi、ΔKd的比例因子分别设定为-0.01、0.01 和0.01。为提升系统稳定性，选用受误差变化影响较小的增量式PID控制器作为核心控制，控算公式为

式中：e(k)为误差；u(k)为控制量。

4 仿真

在Simulink 模块下对基于车床的模糊PID 控制系统进行仿真，并与传统PID控制对比。根据建模结果，选取背吃刀量为1 mm，每齿进给量为0.004 mm，确定传递函数为

以理想状态的阶跃信号作为控制系统的输入，通过MATLAB 中的Fuzzy Logic Designer 工具箱对模糊论域、模糊推理规则、隶属度函数以及去模糊化方式进行设置，并结合PID控制模块实现模糊PID控制。设定Kp为1.5、Ki为3、Kd为1.2，设置时滞为1的Transport Delay 模块模拟信号延迟现象，控制结果见图4a。为验证模糊PID控制的自适应性，设置终值为15、20、25 的阶跃信号，模拟目标功率设置不同的控制情况，结果见图4b。根据仿真结果得出控制系统的动静态特性对比见表4。无干扰条件下，模糊PID 控制与传统PID 控制的响应时间相近，但模糊PID控制下超调量更小，峰值更低，调整时间更短，可见模糊PID 控制的超调现象更不明显，稳态性能更好，精度更高。同样，在阶跃信号不同的条件下，模糊PID的控制效果受外界条件改变的影响不大，自适应性更好。

表4 控制系统特性

5 实验验证

为验证控制系统在实际车削过程中的有效性和可行性，设计了传统车削与恒功率智能控制车削对比实验。车削铝棒直径为20 mm，选用WB9128功率传感器采集功率信号，模糊PID控制算法的实现较复杂，所以选择支持SCL 语言的西门子S7-1200 PLC作为核心控制器（CPU型号为1215C DC/DC/DC），并与组态软件WINCC 通信，实现上位机的数据显示，现场实验平台如图5所示。

图5 现场实验平台图

为模拟复杂的工件表面，将铝棒加工成3个高度分别1 mm、2 mm、3 mm 的台阶；然后采用一刀切的方式对台阶进行车削，刀具在车削3个台阶的过程中背吃刀量分别为1mm、2mm、3mm，见图6。

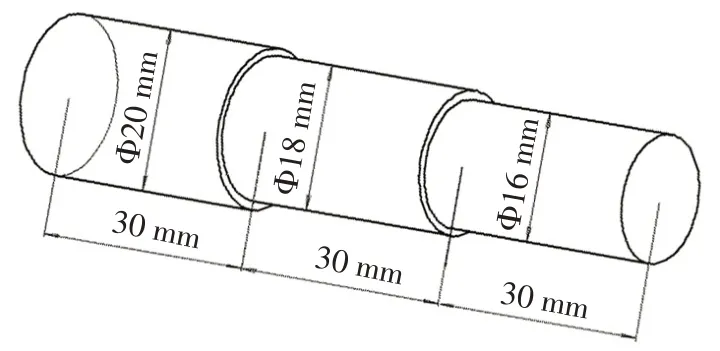
图6 阶梯状工件示意图

为明晰自适应控制系统的效果，首先对工件采取传统车削实验，即在车削过程中设定恒定进给倍率为100，模拟无控制情况的传统车削加工过程。随着背吃刀量增加，主轴功率呈三段台阶式的增长，如图7a 所示。车削第1 个台阶时，主轴功率为757 W，刀具负荷较小，加工效率有较大的提升空间。车削第3 个台阶时，主轴功率较大，最大为1002 W，主轴负载与刀具承受较大负荷，容易造成磨损。恒功率控制车削实验以800W为目标功率，当实时功率超过800 W 时，进给倍率降低；当实时功率低于800 W 时，进给倍率升高，功率维持在目标功率的误差范围，见图7b。由表5 可知，与传统车削过程相比，使用自适应控制系统后，车削过程的加工时长减少了28.24%，能耗降低了36.15%。

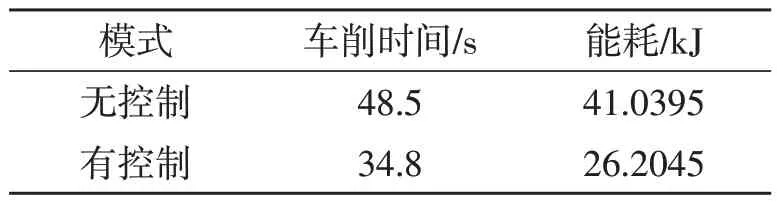
表5 控制前后结果对比

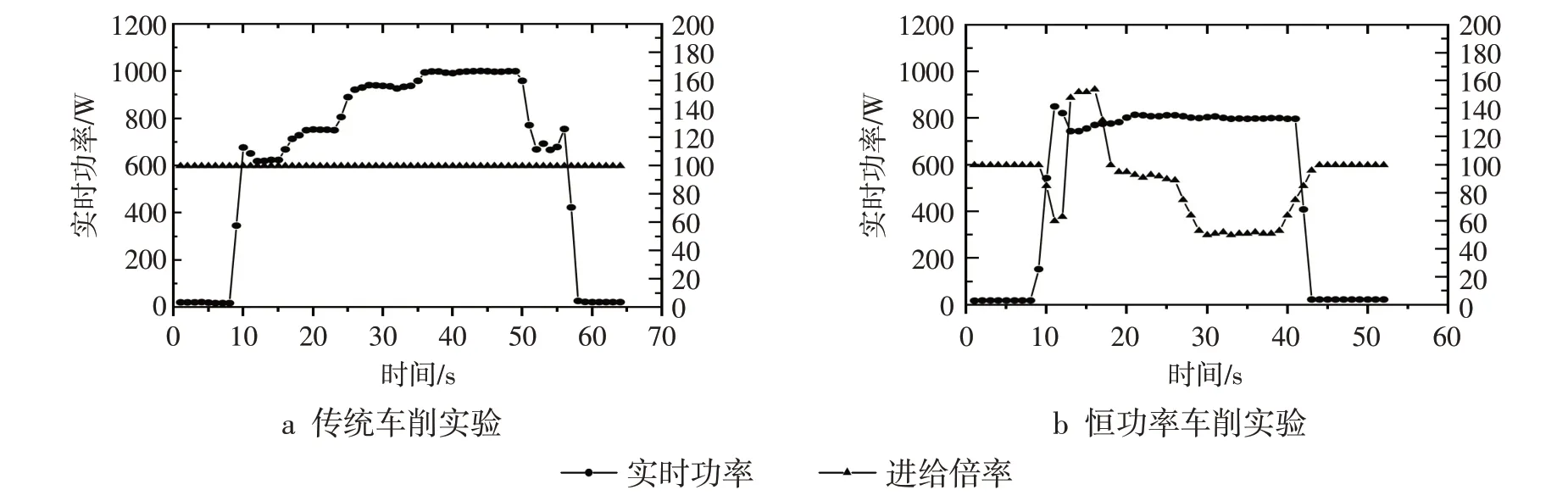
图7 车削实验结果

6 结论

文中提出基于模糊PID 的恒功率车削控制方法。首先设计正交实验，拟合主轴功率与背吃刀量、每齿进给量和主轴转速的数学模型，实现车削加工系统的控制仿真；根据主轴功率与目标功率的误差及其变化率，实时调整PID 控制模块的参数，从而实时调整进给速度，使主轴功率保持在目标功率的误差范围内。经过实验验证，文中自适应控制方法可有效保证主轴功率维持恒定，进而优化车削加工效率、降低能耗效率。