Path Planning of UAV by Combing Improved Ant Colony System and Dynamic Window Algorithm

XU Haiqin(徐海芹), XING Haoxiang(邢浩翔), LIU Yang(刘 洋)

College of Information Sciences and Technology, Donghua University, Shanghai 201620, China

Abstract：A fusion algorithm is proposed to enhance the search speed of an ant colony system (ACS) for the global path planning and overcome the challenges of the local path planning in an unmanned aerial vehicle (UAV). The ACS search efficiency is enhanced by adopting a 16-direction 24-neighborhood search way, a safety grid search way, and an elite hybrid strategy to accelerate global convergence. Quadratic planning is performed using the moving average (MA) method. The fusion algorithm incorporates a dynamic window approach (DWA) to deal with the local path planning, sets a retracement mechanism, and adjusts the evaluation function accordingly. Experimental results in two environments demonstrate that the improved ant colony system (IACS) achieves superior planning efficiency. Additionally, the optimized dynamic window approach (ODWA) demonstrates its ability to handle multiple dynamic situations. Overall, the fusion optimization algorithm can accomplish the mixed path planning effectively.

Key words：ant colony system(ACS); dynamic window approach (DWA); path planning; dynamic obstacle

0 Introduction

An unmanned aerial vehicle (UAV)[1]is a type of aerobat that can be controlled through telecommunication systems or artificial intelligence and is widely used in aerial images[2], electric patrol[3], and other fields[4]. Path planning[5]is an important research field of the UAV, and consists of the global path planning and the local path planning. Global path planning involves finding the optimal path in a static environment to reach the destination from the starting point. Guletal.[6]modified grey wolf optimization based on frequency to speed up the global search safely. Zhouetal.[7]dynamically adjusted the pheromone heuristic and heuristic function factors in the ant colony system (ACS) algorithm to avoid falling into local optimization.

Local path planning[8]involves planning paths in real time to avoid dynamic obstacles in a local environment. Various algorithms are commonly used, including the D*algorithm[9], the dynamic window approach (DWA)[10], and others. Shietal.[11]improved a simulated annealing algorithm by introducing initial path selection and deletion operation for dynamic path planning. Hanetal.[12]achieved dynamic path planning of unmanned surface vehicles by carrying out global path planning based on non-uniform Theta*and dynamically selected DWA local target points. While these algorithms have been improved, they still have performance limitations in the mixed path planning which includes both global and local path planning. This paper proposes the fusion algorithm based on the improved ant colony system (IACS) and the optimized dynamic window approach (ODWA) to achieve the mixed path planning[13].

The following sections are structured as follows. Section 1 provides an introduction to ACS, DWA, and the moving average (MA) method. Section 2 addresses the limitations of ACS and optimizes DWA to handle dynamic obstacles. Section 3 outlines the environment settings and algorithm flow. Section 4 showcases the evaluation metrics, experiments, and analyses. Finally, conclusions are given in section 5.

1 Basic Algorithm

1.1 ACS

The concept of ACS[14]is inspired by the foraging behavior of ants and is applied in practical problem-solving research. Ants use a pseudo-random state transition strategy to select the next grid point:

(1)

(2)

whereJdenotes a random value selected;qandq0refer to the probability and pre-defined probability threshold, respectively, andq0∈ [0,1];τijandηijindicate the amount of pheromone concentration and heuristic information from gridito gridj, withdijrepresenting the distance from gridito gridj, andηij= 1/dij;sis a grid not visited by ants;Cdenotes the set of possible next grid point sets that can be selected;αandβdenote the pheromone heuristic and heuristic function factor, respectively;pijdenotes the transition probability between two points whenqis greater thanq0.

Updates the local pheromones ofτijwhen ants transition from gridito gridj:

τij(t+1)=(1-ρL)τij(t)+ρLτ0.

(3)

Once all the ants have finished path exploration, the pheromone for the contemporary is updated:

τij(t+1)=(1-ρG)τij(t)+ρGΔτij,

(4)

(5)

whereτ0denotes the initial pheromone value ofτij;Qdenotes the pheromone enhancement coefficient;ρLandρGdenote the local and global pheromone volatilization rates;Lmsignifies the total length of the best path globally from the beginning of the run.

1.2 DWA

The central concept of DWA involves optimizing the speed within the dynamic window to find the best solution for the feasible region. This is achieved by assuming an extremely short interval Δt, where adjacent Δtmoves at a consistent speed, and defining the motion trajectory:

(6)

wherevxandvyrespectively represent the UAV horizontal and vertical velocities in a two-dimensional(2D) environment;ωis the angular velocity;θtdenotes the heading angle; DWA samples these parameters to determine the velocity space at the next moment. The constraints are categorized into three specific categories.

Speed limit:

vs={(v,w)|v∈[vmin,vmax],ω∈[ωmin,ωmax]},

(7)

wherevsis the speed limit range;vminandvmaxdenote the minimum and the maximum linear speeds, respectively;ωminandωmaxdenote the minimum and the maximum angular accelerations, respectively.

Acceleration limit:

(8)

wherevddenotes the achievable speed range;avminandavmaxdenote the minimum and the maximum linear accelerations, respectively;aωminandaωmaxdenote the minimum and the maximum angular accelerations, respectively.

Obstacle constraint:

(9)

wheredrepresents the distance between the robot and the nearest obstacle;avandaωare the accelerations for breakage, respectively;vais the set of velocities which allow the UAV to stop without colliding with an obstacle.

vr=vs∩vd∩va.

(10)

Dynamic windows refer to sets of speedsvrthat meet the three constraints above. Any speed within the window can be selected.

1.3 MA method

The MA[15]method is used to smooth out the track. It involves replacing the original value with the average ofmadjacent data points for a sequence calledyk:

(11)

wherem= 2n+1;Nis the number of sequence points.

2 Improved Algorithm

This section discusses how ACS and DWA algorithms can be improved. The ACS algorithm involves adjusting the search and utilizing the elite hybrid strategy to update pheromones. Meanwhile, the DWA algorithm can be enhanced by implementing a retracement mechanism and adding a distance guidance subfunction into the evaluation function.

2.1 IACS

2.1.1Adjustsearchway

Instead of exploration step-by-step, ants use the 16-direction 24-neighborhood search way[16]illustrated in Fig.1 to directly access any grid within the current red grid 24-neighborhood.

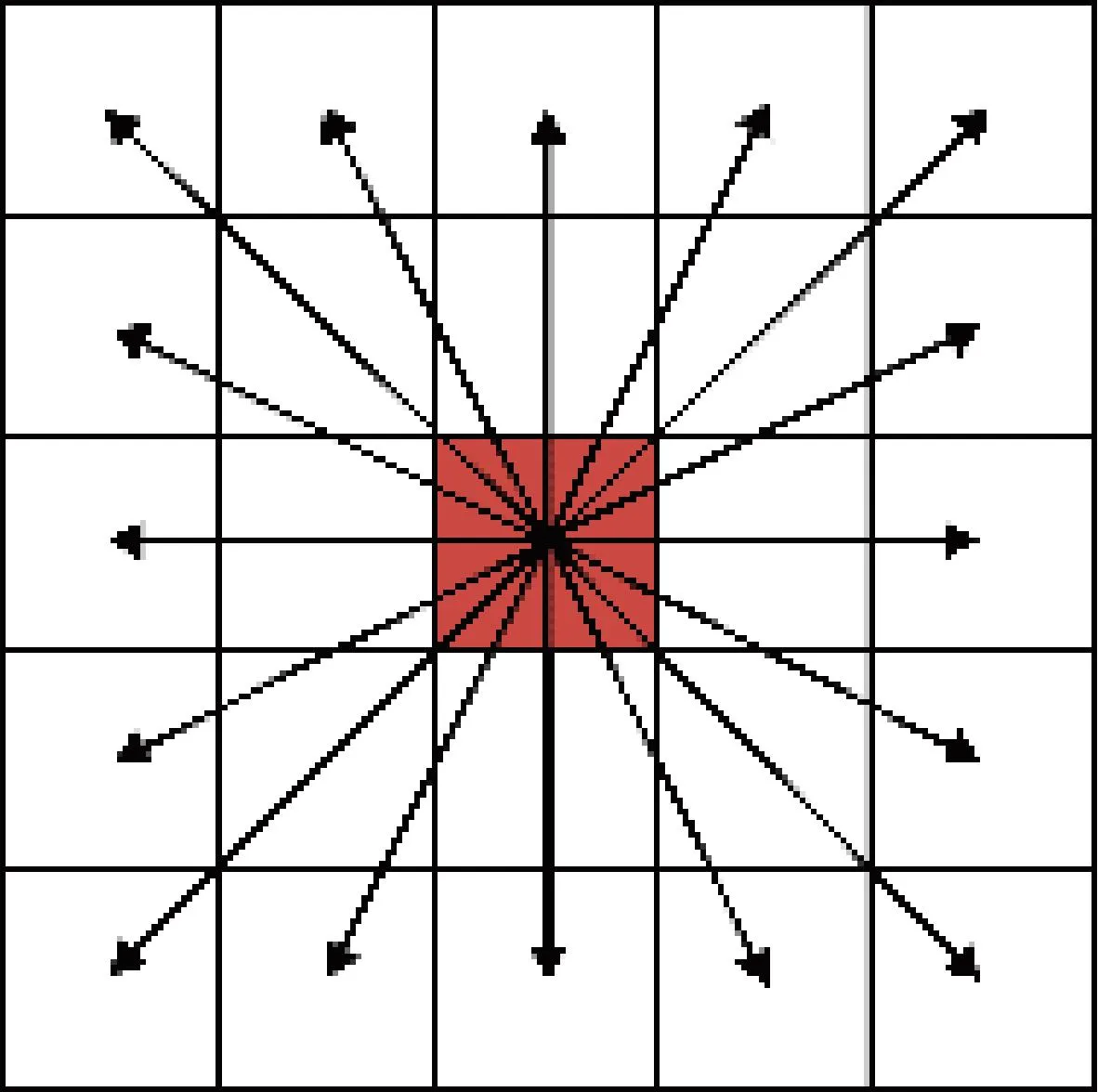
Fig.1 Diagram of 16-direction 24-neighborhood search way

In order to enhance search security, a rule has been established where four adjacent grids of one grid can be considered valid passing and subgoal points for ant colony exploration if they do not have any obstacles. These grids are marked as safety grids and are depicted as white in Fig.2. However, the four neighboring regions of the gray grid have obstacles and can only be used as valid passing points for path exploration.

Fig.2 Safety grids

Fig.3 Grid environment

2.1.2Elitehybridstrategy

During initialization of the pheromone, the grid map is contacted to decrease blind searching in the early stages.ρdenotes the pheromone volatilization factor that is dynamically adjusted, which reduces confused pheromone accumulation in the early stages:

(12)

whereGdenotes the current iteration number;Gmdenotes the maximum number of iterations.

The ACS local update strategy has been abandoned to update only the optimal path of each generation globally.Lcis the contemporary optimal path.Lcis compared withLm(from section 1.1) to enhance the pheromones guidance to improve the algorithm’s search quality. This is called the elite hybrid strategies in pheromone operation:

τij(t+1)=(1-ρ)τij(t)+Δτij+τe,

(13)

(14)

where Δτijis the pheromone of the optimal historical path;τedenotes the elite mixed pheromone;η1andη2are the weighting factors.

2.2 ODWA

2.2.1Modifyevaluationfunction

When DWA performs speed sampling, in order to solve the issue that returns to global path planning after finishing local planning, we have introduced a guide sub-functionL(v,ω) to improve position guidance and to calculate the distance between the current location and the local target point. The speed combination for the robot’s next positionG(v,ω) is defined by

G(v,ω)=αH(v,ω)+βD(v,ω)+γV(v,ω)+ηL(v,ω),

(15)

H(v,ω)=180-θ,

(16)

(17)

(18)

whereH(v,ω),D(v,ω) andV(v,ω) are the subfunctions for the heading angle, distance from the nearest obstacle and velocity, respectively;α,β,γandηare the subfunction’s weights;θis the angle between the target and predicted position;dis the calculated length;dminanddmaxare the set length thresholds;sgandscdenote the current location and the local target point, respectively.

2.2.2Addretracementmechanism

The UAV activates the retracement mechanism when it encounters dynamic obstacles in an adjacent grid. The mechanism makes the UAV return to its previous position and resumes the local path planning while maintaining a safety margin.

3 Algorithm Fusion

3.1 Environment model

Figure 3 displays the environment established through the grid method[17]. The white grid allows free movement, while the black and the red grids represent static and dynamic obstacles. The relationship between theith grid in the grid map and its corresponding 2D coordinates is

(19)

whereadenotes the grid length;Ndenotes the grid level;mod(·) is the complementary function;ceil(·) is the top integral function.

3.2 Algorithm flow

It is worth noting that ACS has certain limitations. It can only identify the best path in static environments, and handling dynamic obstacles is difficult. Fortunately, these limitations can be addressed through the use of DWA. The combination of IACS and ODWA enables the algorithm to respond autonomously to environment changes, efficiently avoiding static and dynamic obstacles. The fusion algorithm uses global path planning data to attain the local target point for ODWA. This results in a more effective mixed path planning approach towards the intended destination. A visual representation of the algorithm flow is shown in Fig.4.

Fig.4 Algorithm flow chart

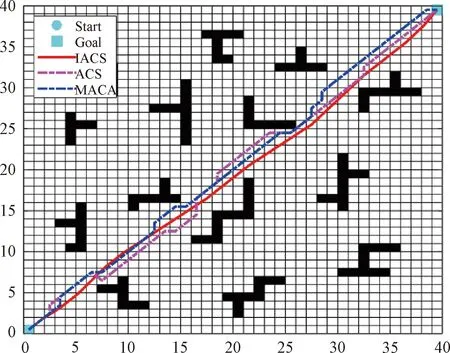
Fig.5 Path planning of 40×40 grid map

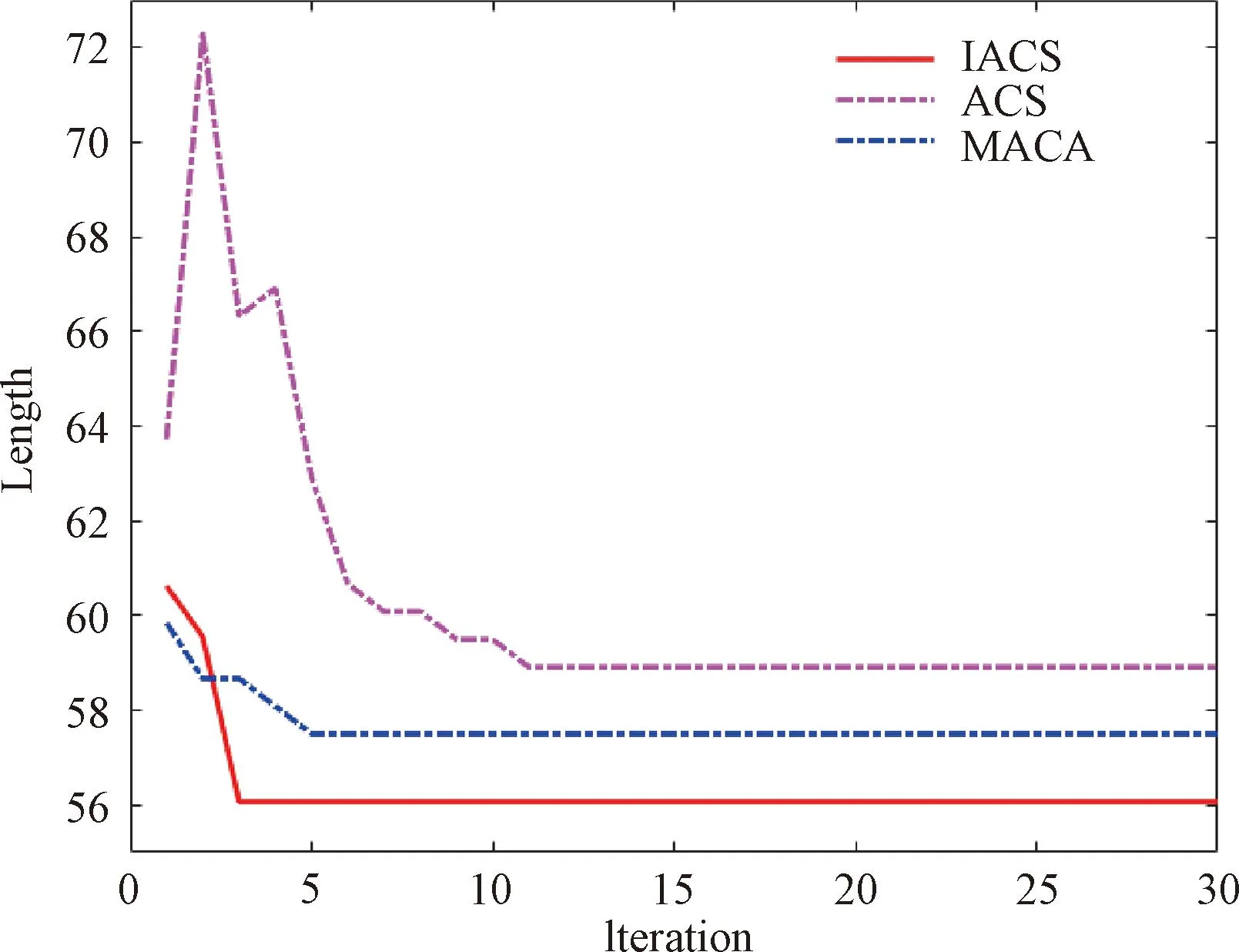
Fig.6 Convergence curve of 40×40 grid map

Fig.7 Path planning of 100×100 grid map

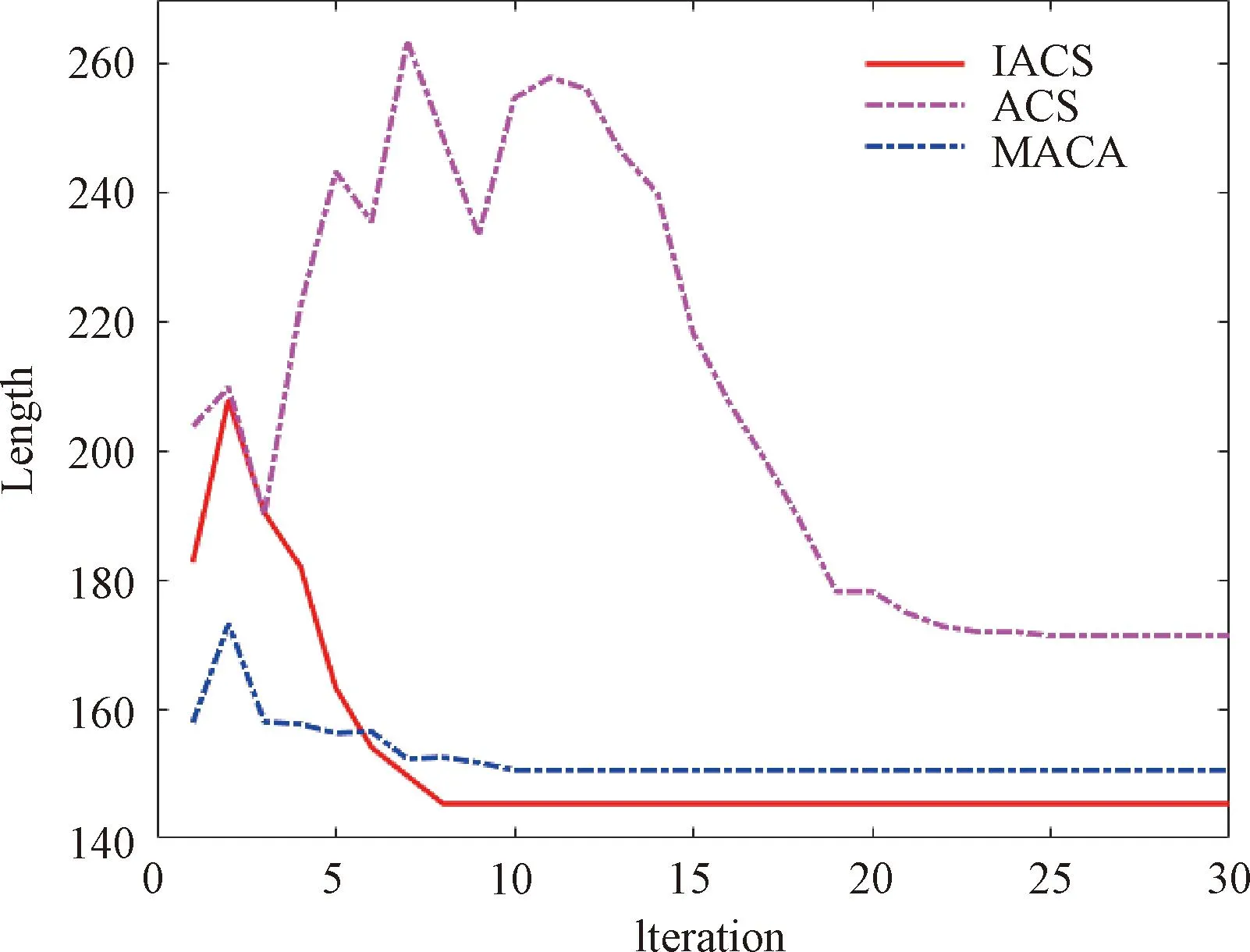
Fig.8 Convergence curve of 100×100 grid map

4 Experiments and Numerical Analysis

The simulation configuration used in this work was the following, Windows 10 64-bit, processor, Intel (R) Core (TM) i7-7700HQ, clocked 2.8 GHz, on-board RAM 8.00 GB, and simulation software Matlab R2021b.

Experimental data are uniformly reserved to 2 digits after the decimal point. ACS algorithm parameters in the experiment are shown in Table 1, and kinematic parameters of DWA are shown in Table 2.

Table 1 ACS algorithm parameters

Table 2 Kinematic parameters of DWA

(Table 2 continued)

4.1 Performance analysis of IACS

In 40×40 and 100×100 grid maps, IACS proposed in this paper, ACS, and the improved algorithm called MACA in Ref. [18] are compared and analyzed.

4.1.1Experimentalsimulationin40×40gridmap

The experimental results shown in Table 3 verify that IACS has better performance in terms of the convergence iteration (3 <5), path length (55.36 <57.50), and runtime (0.51 s< 1.10 s). It is shown in Figs.5 and 6 that the path of IACS is smoother and converges earlier.

Table 3 Simulation data of 40×40 grid map

4.1.2Experimentalsimulationin100×100gridmap

From the experimental results shown in Table 4, it can be found that the proposed IACS has the highest efficiency. IACS generates the least path length (142.76 <150.55 <171.42), the smallest convergence iterations (8 <10 <25), and the shortest runtime (3.70 s <7.26 s <8.70 s). Path planning in a 100×100 grid map still converges swiftly, as shown in Figs.7 and 8.

Table 4 Simulation data of 100×100 grid map

IACS can obtain a safe and smooth optimization path in two different environments, better than ACS in terms of the convergence speed and the global search ability, achieving the expected goal of IACS.

4.2 Performance analysis of ODWA

ODWA uses a retracement mechanism to prevent issues in terms of potential deadlock situations. The specific process of the retracement mechanism is shown in Fig.9(b). The sign of grid colors in the map is shown in Table 5.

PointAand pointCare the starting point and the dynamic obstacle for the local path planning, respectively. PointBis the waypoint for the local path planning.

UAV starts local path planning from pointA, and when runs to pointB, and the fusion algorithm has detected a risk of collision at pointC. Currently, the fusion algorithm calls the retracement mechanism to make UAV withdraw from pointBto pointAand continue the local path planning.

4.3 Dynamic obstacle avoidance analysis of the fusion algorithm

The fusion algorithm’s global path planning and local path planning abilities for the mixed path planning are tested, and various dynamic obstacles are placed within a 20×20 grid map.

The path planning task is accomplished by the fusion algorithm in a global path planning as shown in Fig.10. When faced with dynamic obstacles, the algorithm depends on IACS to gather navigation information and determine the start and the goal points for local planning. This results in a mixed path-planning approach as illustrated in Fig.11.

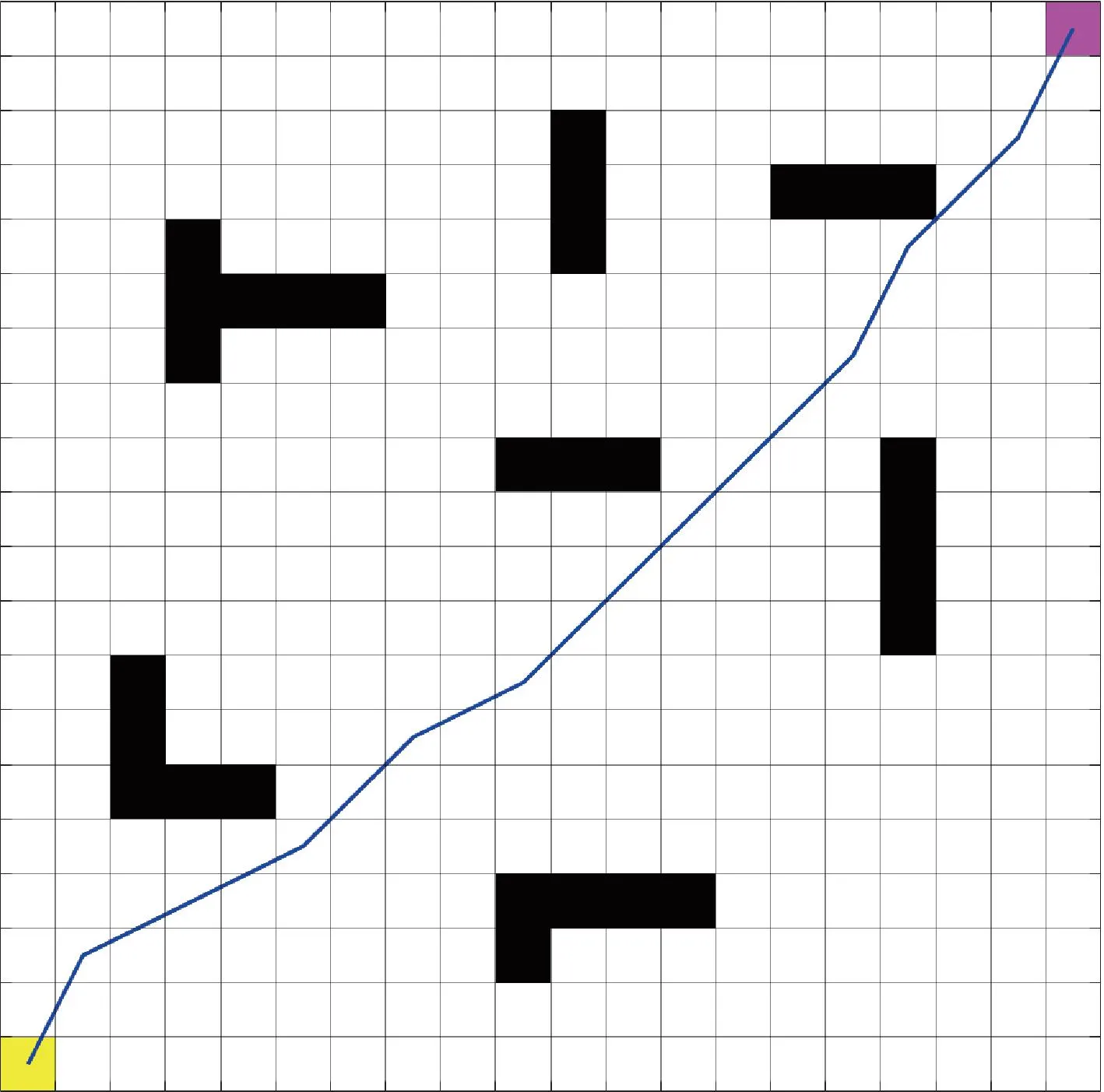
Fig.10 Grid environment without dynamic obstacles

Fig.11 Grid environment with two dynamic obstacles

In Fig.12, the mixed path planning concrete process is displayed. The first stage involves global path planning carried out by IACS as shown in Fig.12(a). ODWA of the fusion algorithm is called, and responsible for the local path planning as shown in Figs. 12(b) and 12(c), which involves dodging dynamic obstacles and exploring the path. Once the local path planning is completed as shown in Fig.12(d), IACS is called upon to complete the global path planning for the second segment in the third stage, after which the task is finished.

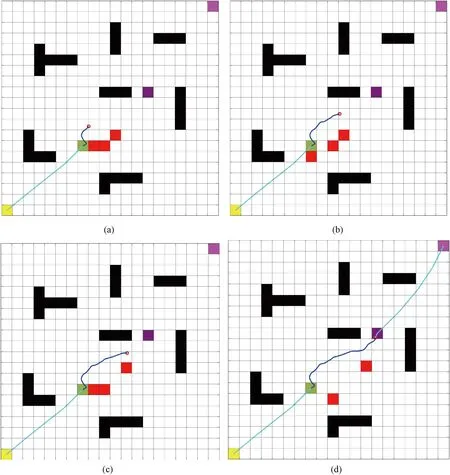
Fig.12 Mixed path planning process with three dynamic obstacles: (a) end of the first global path planning; (b) local path planning; (c) end of local path planning; (d) the second global path planning

The fusion algorithm’s performance was tested 100 times under dynamic obstacle scenarios. The results of these operations are shown in Table 6.

Based on Table 6, the fusion algorithm of IACS and ODWA, as proposed in this paper, can complete the mixed path planning in a mixed environment. However, the results also reveal that the success rate of the fusion algorithm decreases as the number of dynamic obstacles increases. This is due to the complexity of the environment where multiple dynamic obstacles move randomly simultaneously. The algorithm may cause errors in the judgment of multiple adjacent dynamic obstacles, sometimes resulting in algorithm planning failures.

5 Conclusions

This study presents the fusion algorithm that combines IACS and ODWA to address the inefficiency and difficulty of planning in a mixed environment. The algorithm includes a 16-direction 24-neighborhood search way and a safety grid to enhance the path search speed. Additionally, an elite hybrid strategy is introduced to boost global optimum. DWA is incorporated to tackle the inability of IACS in the local path planning. Two different environment experiments are conducted and the effectiveness of IACS is validated. Further, ODWA is tested in various dynamic obstacles. The experimental results confirm the effectiveness of the fusion algorithm in the mixed path planning.

The fusion algorithm should be further improved, as its success rate in completing the mixed path planning needs to be 100%. When faced with complex dynamic environments, the algorithm may sometimes encounter a deadlock that cannot calculate the next safe position with the adjacent grid having multiple dynamic obstacles. It requires further investigation in future research to improve the fusion algorithm program for handling dynamic obstacles. Furthermore, expanding into three-dimensional space is an essential aspect of the fusion algorithm’s scope.