Cleaning of Multi-Source Uncertain Time Series Data Based on PageRank

GAO Jiawei(高嘉伟), SUN Jizhou(孙纪舟)

Faculty of Computer and Software Engineering, Huaiyin Institute of Technology, Huai’an 223003, China

Abstract：There are errors in multi-source uncertain time series data. Truth discovery methods for time series data are effective in finding more accurate values, but some have limitations in their usability. To tackle this challenge, we propose a new and convenient truth discovery method to handle time series data. A more accurate sample is closer to the truth and, consequently, to other accurate samples. Because the mutual-confirm relationship between sensors is very similar to the mutual-quote relationship between web pages, we evaluate sensor reliability based on PageRank and then estimate the truth by sensor reliability. Therefore, this method does not rely on smoothness assumptions or prior knowledge of the data. Finally, we validate the effectiveness and efficiency of the proposed method on real-world and synthetic data sets, respectively.

Key words：big data; data cleaning; time series; truth discovery; PageRank

0 Introduction

Numerous data types play a vital role as a consequence of the rapid growth of big data and internet technology. The time series data gathered by sensors are also used in many spheres of life, including the measurement of travel data for planes, cars, and other vehicles[1], the real-time monitoring of traffic flow, the real-time monitoring of temperature and humidity in intelligent agriculture,etc. People improve their decision-making through analysis of a large amount of data which are collected in real-time from sensors.

Due to many issues including accuracy, quality, and human factors, the time series data gathered by multiple sensors cannot be immediately used as the final data for analysis and study. With a vast amount of information, determining whether the data contain the needed truth or which sources provide more precise data is a challenge. Several frameworks have been investigated to address this issue[2-5]. The Mean[6]and the Median[6]methods are the simplest ones. However, they have an apparent flaw: these data sources are viewed as equally trustworthy, which is typically not the case in real life. After examining several different truth discovery methods for time series data, we discover that the online truth discovery (OTD) method[7]and the RelSen method[8]produce better results and can effectively clean time series data. However, they still have stringent requirements for smoothing and prior knowledge of the data.

In this paper, in order to develop a more comprehensive method that can be applied to a wide range of data, we propose a new multi-source uncertain time series data cleaning method, truth discovery based on PageRank[9](TDBPR). Commonly, the more accurate a sample is, the closer it is to the truth. Therefore, we combine the method with Google Chrome’s PageRank method and calculate the weights by the PageRank method to determine which source has higher reliability. In this way, the reliability and the truth of the source can be learned from the data in an unsupervised manner. Specifically, our contributions are listed as follows.

1)We propose TDBPR and formalize the truth discovery into a PageRank method which has fewer data prerequisites and is more flexible with various data sets.

2)The proposed method combines the PageRank method and finds a more accurate estimated truth by constantly calculating the weights to be assigned.

3)Experiment on real-world and synthetic data sets verifies the effectiveness of the method in truth discovery.

The remaining part of this paper is organized as follows. In section 1, some related work on truth discovery and time series cleaning is presented. In section 2, the data model is described and the problem is formalized. Then, the method is described in detail in section 3. Section 4 presents the experiments and results. Finally, this paper is concluded in section 5.

1 Related Work

Time series data are now crucial data for analysis and strategic decision-making. However, errors are commonly found in time series data. The conclusions or rules are bound to be inaccurate if the information is not corrected. Numerous time series cleaning methods have emerged in the face of difficulties such as large data volumes, high error rates, and complex causes of error generation. In Ref. [10], the existing cleaning methods are divided into four categories: smoothing-based methods which are commonly used to eliminate data noise especially numerical data noise, such as Interpolation[11]and Kalman filter[12]; constraint-based methods; statistical-based methods; time series anomaly detection methods. For different domains, Dingetal.[13]proposed an industrial time series cleaning system with a user-friendly interface to use results and log visualization during each cleaning process. EDCleaner was designed for social networks, and it could detect and clean the data by features of statistical data fields[14]. PACAS was proposed for data cleaning between service providers and customers[15].

As a part of data cleaning, numerous truth discovery methods[16-19]have been developed with different focuses, such as privacy-preserving truth discovery[20-21]and source selection[22]. Early multi-source truth discovery methods use majority voting, and the data with more occurrence times are the estimated truth. However, this method lacks judgment on the reliability of data sources, so the accuracy is often low. Yinetal.[23]proposed the iterative calculation of the source weight and the estimated truth, and introduced the concept of the source consistency hypothesis which was widely adopted in other truth discovery methods. In 2-Estimates, complementary voting was used by assuming that each object had only one truth[24]. While 3-Estimates augmented 2-Estimates by considering the difficulty of obtaining the truth for each object[24]. For discovering continuous object truth, Yangetal.[25]proposed a semi-supervised truth discovery method. Yaoetal.[7]proposed an online truth discovery(OTD) method that combined time series forecasting and considered facts with smooth evolution and seasonal trends. Fengetal.[8]proposed a method that combined data cleaning and assigned reliability parameters to data sources.

In cleaning multi-source uncertain time series data methods, the OTD method and the RelSen method are the primary methods. Both methods have a strong theoretical basis, and the experimental results can be calculated very close on some data sets. Nevertheless, they both have strong assumptions, require data sets to be smooth and periodic, or require a large number of manual parameter settings, which limits the usability of the methods. Therefore, this paper proposes a more adaptive multi-source time series cleaning method without parameter settings or data smoothing.

2 Problem Statement

Time series data are ordered sequences of real numbers like temperature or humidity,C=[c1,c2, …,cj,…,cn]T(1≤j≤n) wherecjis a random variable that represents the data obtained at thejthtime point, butcj’sground truth is unknown because of the noise in the sequence. The multi-source time series data are collected withmdata sources such as sensors to get the sample data. Theithsource sends the time series data asSi=[si,1,si,2,…,si,j,…,si,n]T(1≤i≤m). Since the source is inaccurate, the claimsi,jis not directly equal to the ground truthxj, and has an error termei,j. The relationship satisfiessi,j=xj+ei,j, meaning that the measured value is equal to the arithmetic sum of the ground truth and the error. It is assumed that the error generated by each sourceSiis a random variableEithat obeys a normal distribution, and the meanμof this normal distribution is 0. This means that there is no systematic error in each source, and the standard deviation is an unknown random variableσi.

In this way, our unknown data are the ground truth seriesX=[x1,x2, …,xj, …,xn]Tand the standard deviation of each source∑={σ1,σ2,…,σm}. Here we consider that the errors generated by each source are independent of each other, and the source’s errors at different moments are also independent of the others.

We can now define the problems of interest in this paper.

InputThe claimed series samplesS={S1,S2, …,Si,…,Sm}(1≤i≤m) contains errors, where eachSirepresentsSi=[si,1,si,2, …,si,j, …,si,n]T(1≤j≤n).

InferringtruthGiven an input claimed seriesSwith no truth information, we intend to output the estimated truthX*.

InferringsourcequalityMeanwhile, we also provide the weight which is used to determine how reliable a source is. The higher its weight is, the more reliable it is.

3 Methodology

This section provides a detailed introduction to TDBPR, including how it calculates the weight and gets the estimated truth.

3.1 Theory

We consider that a more accurate sample is closer to others. It can be understood from Fig.1.

Fig.1 Sample distribution

Each point in Fig.1 represents a sample distributed in a two-dimensional plane, and those distributed in the dense center are more precise samples, as can be proved from the Euclidean distancedE:

(1)

When calculating the distance expectation between two samples,S1=X+E1andS2=X+E2. Since the error expectation of each data source is 0, the distance expectationdecan be simplified as

(2)

whereD(·) is the variance fuction.

From Eq. (2), it can be seen that the distance of each sample is proportional to the variance of its error term. Thus the more accurate the sample is, the smaller the distance is.

3.2 PageRank

In practical applications, there is a great deal of data in graphs, the internet and social networks that can be considered as graphs. PageRank, as a ranking of the importance of web pages, is a representative method for link analysis in graphs[26]. It configures the initial PageRank value of each page as 1/m, wheremis the number of pages. The PageRank value after each iteration determines how influential a page is. The higher the value is, the greater the influence of the page is. The PageRank value is calculated by

(3)

The importance of the current page is determined by the latest PageRank value obtained from multiple iterations. This is similar to our proposed idea of calculating the distance between data to determine its reliability, so it is decided to calculate the weight of each source based on PageRank.

3.3 Weight and truth computation

Firstly, all data sources should have the same initial weights, and the sum of the initial weights should be one. We set

(4)

to denote the weight of sourceSiat the initial moment.

Then, the iterative process is entered to distribute the weights of each source according to the distance from other sources, or it is understood that each source obtains the weight based on the distance information from other sources. The iterative equation is

(5)

(6)

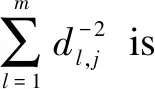
This iterative process continues until convergence, and the weight vectorw=[w1,w2,…,wm]Tcan be obtained. Based on the weight information, the truth can be estimated by the weighted average:

(7)

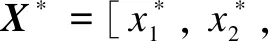
Fig.2 Truth discovery based on PageRank

It can be seen that the time complexity of TDBPR isO(nm2+tm2), wherenis the sequence length,mis the number of sources, andtis the number of iterations.

4 Experiments

In this section, we experimentally evaluate and compare TDBPR with baseline methods on real-world and synthetic data sets.

4.1 Evaluation metrics

In experiments, we use the following two evaluation metrics to evaluate each method.

The mean absolute error (MAE)EMAis

(8)

The root mean square error (RMSE)ERMSis

(9)

Both metrics represent the magnitude of the error by two arithmetic means. MAE is more indicative to small errors, while RMSE focuses more on large errors. For both MAE and RMSE, the lower the value is, the closer the estimated truth to the ground truth is, and the better the performance is.

4.2 Experiments on real-world data

To verify that TDBPR has validity in various situations, we find 85 internationally published data sets with a variety of domains and some data types that also show smoothness and periodicity. The data sets have a certain authority. Experiments are conducted by adding random noise to the collected real-world data sets.

We compare TDBPR with several proposed methods. The Mean method takes the mean value of the data sets as the estimated truth. The Median method takes the median of the data sets as the estimated truth. The OTD method contains two components: the seamless integration of truth discovery and time series analysis that enhances each other and infers the estimated truth in a smooth and periodic time series. The RelSen method is the latest truth discovery method for numerical data. Firstly, it assigns a reliability score to each sensor that can be dynamically updated according to the latest measurement error of the sensor in a sliding window. Then the reliability score is used to eliminate the measurement error of the sensor. Finally, it cleans the data and gets the estimated truth.

The experimental results show that TDBPR has a certain superiority over the other four methods in 85 data sets. Due to the large number of experimental results, only five representative results are listed in Table 1.

As there are numerous data in each set, the Mean and the Median methods make the mean and the median data as the estimated truth, so they are unstable and have a wide margin of error. The OTD method does not perform better in these large random data sets because it mainly performs well on data that are smooth and periodic. At the same time, due to the large data sets in the experiment, the RelSen method cannot set the parameters in advance for each data set, instead, it sets the same parameters, which makes it impossible to show efficient performance. On the contrary, the TDBPR method only focuses on the distance between sample points. More weight will be assigned if the sample is closer to others, so the degree of sample dispersion and complexity have little influence on TDBPR. Due to the lack of complex prerequisite requirements, TDBPR performs better in the face of more random and featureless data so that it can be applied to a broader range of data with more adaptability.

4.3 Experiments on synthetic data

This series of experiments on synthetic data sets aims to demonstrate the performance of TDBPR on various synthetic data set sizes and investigate the relationship between its time cost and sequence length.

We randomly generate a large amount of data to test whether TDBPR can always present a better performance on data sets at different sequence lengths. The experimental results show that TDBPR consistently outperforms the other four methods in a variety of samples with a multiple of ten in length. Part of the experimental data are shown in Table 2.

Table 2 Performance of different methods on synthetic data sets

Even though the error of TDBPR is larger than that in experiments on real-world data sets, it is still better than the other four methods. Experiments show that TDBPR can perform well with both smooth and non-smooth data, which is due to the fact that TDBPR only focuses on the distance between samples to estimate the truth.

We also investigate how the length of the sample sequence is correlated with its time cost. By recording the time cost under different sequence lengths in Fig.3, we find that as the sequence length increases, the time cost tends to grow steadily. It is because the time complexity of TDBPR isO(nm2+tm2) of which the sequence length has a linear relationship with the time cost, which proves that TDBPR has good scalability.

Fig.3 Time cost of TDBPR at different sequence lengths

5 Conclusions

Time series data generated by multi-source often contain noise points. In order to extract trustworthy information from this data, we propose TDBPR with adaptability and wide applications. The main logic behind TDBPR is fairly straightforward. TDBPR considers that the weight of estimating reliability can be determined according to the distance between sample points and other points. Based on the PageRank method, we set the initial weights and allocation ratio of subsequent weights. TDBPR does not rely on smoothness assumptions or prior knowledge of the data. Through extensive experiments on real-world and synthetic data sets, the effectiveness of TDBPR in truth discovery is demonstrated.