Effects of plasma radiation on the nonlinear evolution of neo-classical tearing modes in tokamak plasmas
2022-06-01ShuaiJIANG姜帅WeikangTANG汤炜康LaiWEI魏来TongLIU刘桐HaiwenXU徐海文andZhengxiongWANG王正汹
Shuai JIANG (姜帅), Weikang TANG (汤炜康)Lai WEI (魏来),Tong LIU (刘桐), Haiwen XU (徐海文) and Zhengxiong WANG (王正汹)
Key Laboratory of Materials Modification by Beams of the Ministry of Education, School of Physics,Dalian University of Technology, Dalian 116024, People’s Republic of China
Abstract The effects of plasma radiation on the nonlinear evolution of neo-classical tearing modes are investigated based on a set of reduced magnetohydrodynamic equations.It is found that the radiation can reduce the pressure near the rational surface.During the nonlinear evolution, the magnitude of perturbed bootstrap current is drastically enhanced in the presence of the radiation.Besides, the radiation can increase the growth rate of the magnetic islands by diminishing the pressure,such that the magnetic islands do not saturate compared with that without radiation.On the other hand, with the increase of the ratio of parallel to perpendicular transport coefficientthe reduction of pressure can further increase the growth rate of magnetic islands in the presence of plasma radiation.Finally, the mechanisms of the destabilizing effects driven by the radiation are discussed in detail as well.
Keywords: neo-classical tearing mode, radiation, MHD instability
1.Introduction
The macroscale magnetohydrodynamic (MHD) instabilities have been continually concerned to ensure steady-state operation in tokamak plasmas [1-10].The neoclassical tearing mode(NTM),one kind of MHD instabilities driven by the loss of bootstrap current inside the seeded magnetic islands,can greatly degrade the confinement and even lead to major disruptions [11-20].In the [13], it is indicated that (2, 1)NTM is potentially the most serious one as it always results in severe energy confinement degradation and can lead to disruptions.It is therefore significant to determine the scaling behavior for the(2,1)mode of NTMs in tokamak[4,12,13].On the other hand, the NTM has been observed in many experiment devices such as TFTR [14], ASDEX Upgrade[21] and DIII-D [22].These experiments have demonstrated that the NTM can affect the heat transport and equilibrium of plasma, reducing the confinement time of plasma energy in the nuclear fusion, which is extremely detrimental during the discharge[13,14,21-23].In short,the NTM is greatly prone to being produced and results in deleterious consequences.
During tokamak discharge,plasma radiation is one of the most crucial mechanisms of plasma energy loss, and plays significant roles in the development of MHD instabilities[24, 25].In general, there are three principal types of radiation, namely the bremsstrahlung radiation, the electron cyclotron radiation and the impurity radiation[26-28].In the experiments, furthermore, the radial and poloidal evolutions of the impurity radiation are observed in JET.Then the mechanism on how the impurity radiation influences the MHD instabilities has been attempted [26].It is worth emphasizing that the heat flux generated by the auxiliary heating from the core plasmas is shielded by the magnetic islands, such that the heat flux of the auxiliary heating only flows outside the magnetic islands along the X-point [27].Consequently, the energy in the magnetic islands primarily depends on the Ohmic heating and the radiation cooling.In particular, some disruptions are the result of the plasma radiation, and hence the explorations on disruptions have been carried out [28, 29].Suttrop et al observed the current contraction phase beginning with the growth of (3,1)islands due to the cooling effect of the carbon impurity radiation at the high-q density limit in ASDEX Upgrade [30].Teng et al studied the thermal perturbations inside and outside magnetic islands and found that the large magnetic islands at the density limit can be induced by the impurity radiation [31, 32].However, it should be mentioned that the electron cyclotron radiation is not taken into account in the work of Teng et al[32].Perkins and Hulse analytically investigated the effect of the ratio of the radiated power to the Ohmic heating[33].The density limit disruptions caused by the impurity radiation are practically coincident with the current decay at the safety factorq=2 in JET[26].A radiation-drivenm=2 magnetic island near the density limit is observed in EAST, and anm=1 sideband mode is also driven in the meanwhile,which brings about an internal crash appearing as a large change of the temperature [34].Them=2 magnetic island grows so that the whole cross section is gradually filled and eventually the disruption event occurs [35].A numerical simulation of the radiation driven tearing modes is conducted by using the 3D toroidal geometry MHD code CLT [24].It is found that the width of the magnetic islands increased over 20% of the minor radius (disruption scale).Generally, the plasma radiation, as one of the most important energy loss mechanisms,can destabilize the MHD instabilities and critically destroy the long pulse discharge of tokamak.Despite that the radiation effects have been extensively investigated,it remains a crucial concern in tokamak to understand the roles of radiation effects on the NTMs.
In this work, we study the radiation effects during the nonlinear evolution of NTMs with different bootstrap current proportions by using a reduced MHD model.It is clearly demonstrated that with increasing the plasma radiation, the pressure is reduced and then perturbation of pressure near the rational surface is increased.At the same time, the radiation can increase the width of magnetic islands and furthermore greatly destroy the quasi-steady-state of tokamak operation.In section 2, the modeling equations are introduced.The results of numerical simulations are presented and the relevant physical mechanisms are discussed in section 3.1.Furthermore, section 3.2 shows the effects of the ratio of transport coefficientsunder the plasma radiation.Finally, a summary of these relevant conclusions in this paper and the prospect of the next work are presented.
2.Modeling equations
The nonlinear evolution of the NTMs with the existence of radiation, is investigated by reduced MHD equations in the cylindrical geometry(r,θ,z) .The normalized three-field equations, including the equation of the vorticity field, the equation of the magnetic flux and the equation of the pressure,are as follows:
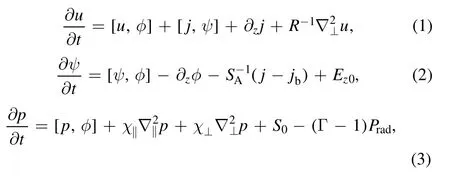

withR0being the major radius of the tokamak.
In the last term in equation(3)Pradis the radiation power density, including the bremsstrahlung radiationPband the electron cyclotron radiationPc.By using the Born approximation, the bremsstrahlung radiation and the electron cyclotron radiation are expressed as follows [36]
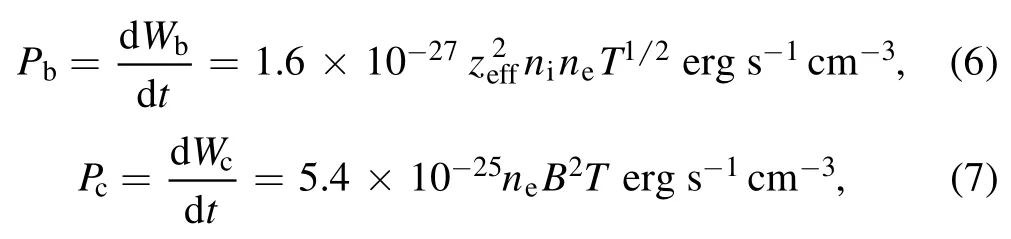
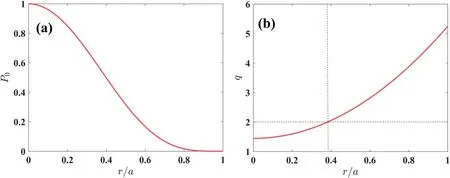
Figure 1.(a) Initial equilibrium pressure profile, (b) safety factor q profile.
whereWb,Wc,ni,ne,B,Tare the power loss of the bremsstrahlung radiation and the electron cyclotron radiation,ion densities (including background ions and impurities),electron densities, the normalized magnetic field and the temperature, respectively.In the case of more than one ion species, ionic charge is written asTherefore, the larger the charge number of impurities is, the greater proportion of the bremsstrahlung is.Here, the conversion relationship between the temperature T and the pressure p is p =nkT,wherek is the Boltzmann constant.
It can be measured that certain kinds of impurities are produced in tokamak edge during the discharge.Impurity radiation is one of the main energy sources of the radiation cooling and mainly originated from the magnetic islands[26].Obviously, the impurity accumulation at O-point of the magnetic islands is the maximal,while it is the minimal at the boundary.Thus, it is assumed that the impurity is Gaussian distribution in the magnetic islands [24]:
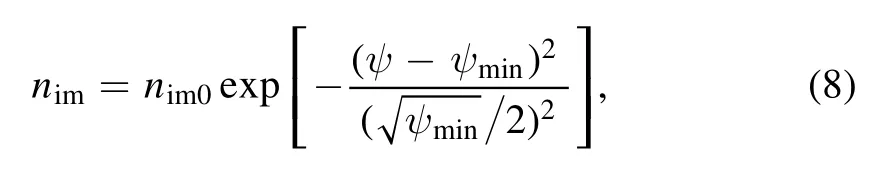
wherenim, nim0andψminare the impurity density, the impurity density at the O-point in magnetic islands and magnetic flux at O-point of magnetic islands,respectively.In this work, the radiation of O-point of the magnetic islands is calculated through equations (6)-(8), and then it is assumed that the radiation in the magnetic islands is Gaussian distribution:
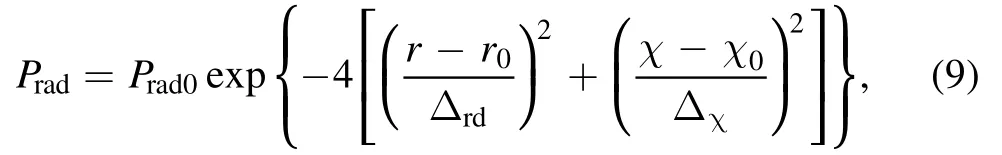
where Prad0is the radiation at the O-point in magnetic islands.(r0, χ0)is the center of the Gaussian distribution.Δrdis the half deposition width in the radial direction andΔχis the half deposition width in the helical angle direction during this model.In fact,we make two assumptions in the model:one is that the densities of impurities present the Gaussian distribution in the magnetic island, and another is that the radiation distribution in the magnetic island also presents Gaussian distribution.Since the impurity radiation is dominant in all radiation,the distribution of radiation in the whole space is basically Gaussian distribution according to the first assumption, which is the reason for making the second hypothesis.If the radiation distribution is truncated around the magnetic island, numerical instability will appear in the calculation.Therefore,we can only take out the real radiation value of O-point in the magnetic island, and then reverse the approximate Gaussian distribution in the magnetic island through equation (9).
Equations(1)-(3)can be solved by an initial value code:MDC (MHD @ Dalian Code) [11, 15-19].The two-step predictor-corrector method is applied in the time advancement.To solve these equations(1)-(3),two different methods are used in different directions.In the radial direction, the finite difference method is employed, while the pseudospectral method is used for the poloidal and the toroidal directions.The initial pressure and safety factor q profiles are chosen as
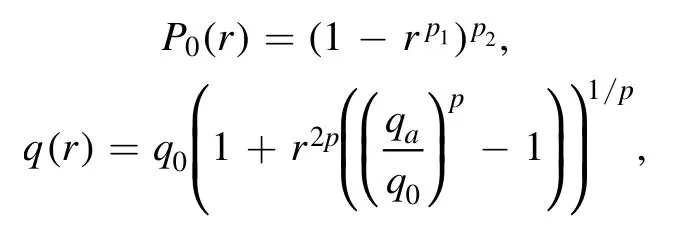
and the plasma rotation is considered by setting
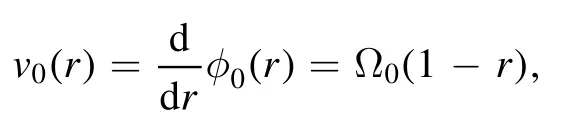

Up to now,it has been planned to choose tungsten as the upper and lower divertor materials of EAST [37, 38].In the future tokamak,moreover,tungsten will be selected as the first wall material in ITER [39], and then tungsten impurities must inevitably be produced during the sputtering process.Therefore,tungsten is necessarily studied as the source of the impurity radiation in this work.
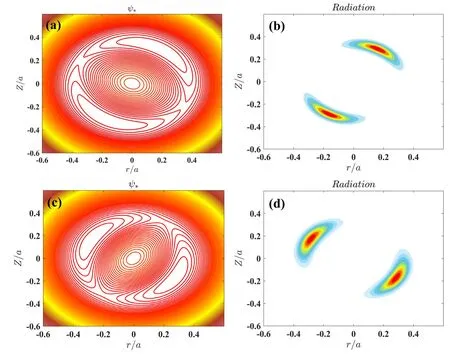
Figure 2.Typical contours of (a) magnetic flux att = 50 τA,(b) radiation att = 50 τA,(c) magnetic flux att = 170 τA,(d) radiation at t =170τ Awith fb =0.3.
3.Numerical results
3.1.Effects of radiation
In this section, the effects of the plasma radiation on the NTMs are discussed.Particularly, tungsten is chosen as the main source of the impurity radiation and we take nim0= 10-4neto calculate the effects of the impurity radiation.As shown in figure 2, the radiation only appears inside the magnetic islands,which is consistent with that mentioned in[27].It is prerequisite that the spatial scale of the radiation region expands correspondingly with the growth of the magnetic islands.Furthermore, the radiation region rotates along with the plasma rotation.Accordingly, MDC can ensure that the radiation is consistent with the change of magnetic islands, as shown in figures 2(b) and (d).
The typical contour plots of the plasma pressure with and without radiation are shown in figure 3.It can be observed that, in the presence of radiation, the pressure reduces drastically inside the magnetic islands and presents a concave structure,which can be observed obviously at325 τA.Besides,the pressure in the core region significantly decays at325Aτ with the plasma radiation.Obviously, the pressure on the resonant surface with radiation is smaller than that without radiation because the radiation cooling can lead to the energy loss near the rational surface.Moreover, it can also be seen qualitatively from the equation (3) that the presence of the radiation can reduce the pressure, and the transformation of the pressure depends on the spatial scale of the radiation cooling.Consequently, the plasma radiation has a significant effect on the evolution of the pressure,decreasing the pressure nearby the rational surface domain substantially.
The eigenmode structures of m /n = 2 / 1 for the perturbation of pressure with fb= 0.3at t =245τAare shown in figure 4, where m andn are the poloidal mode number and toroidal mode number, respectively.It is found that in the presence of the radiation,the amplitude of the perturbation of pressure with m /n = 2 /1on the rational surface is larger than that without radiation.Moreover, as shown in figure 5, the magnitude of the bootstrap current perturbation inside the magnetic islands is enhanced due to the radiation, which indicates that the total perturbation of current increases.In other words, the plasma radiation can increase the perturbation of pressure inside the magnetic islands,and thus increase the perturbation of bootstrap current, resulting in the enhancement of instabilities.
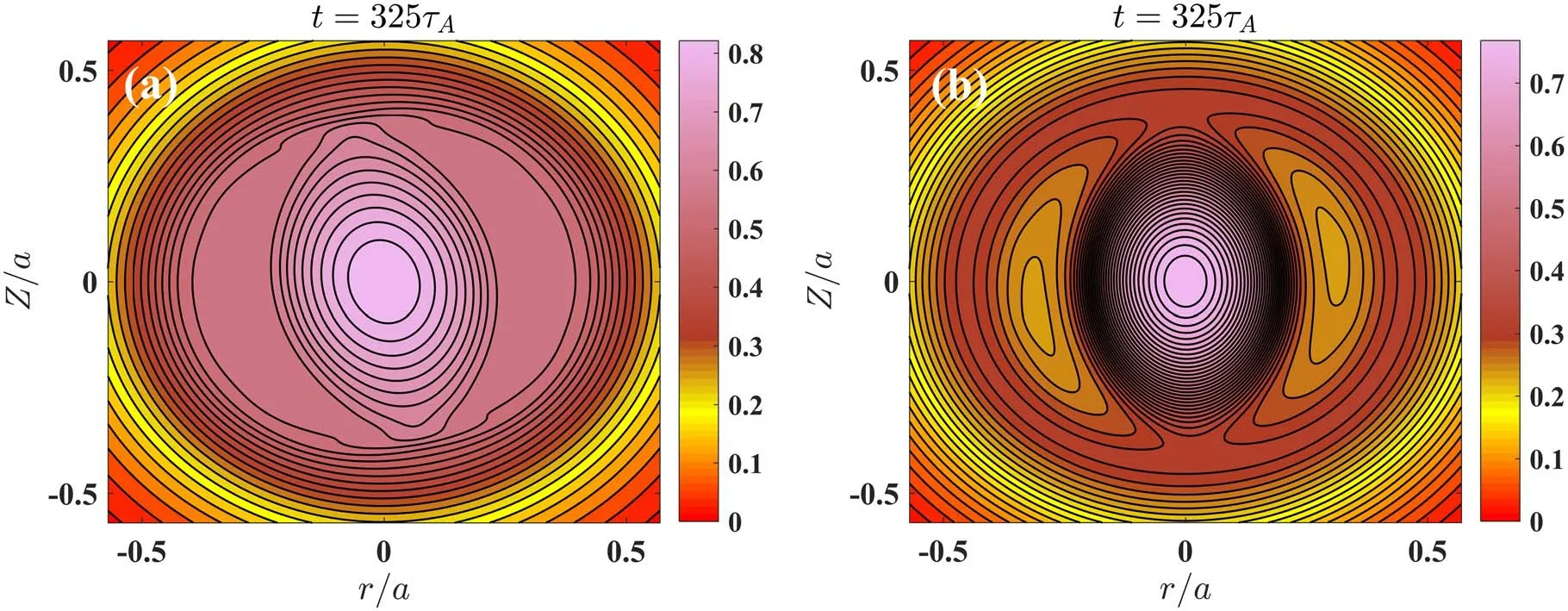
Figure 3.Typical contours of pressure with fb = 0.3att = 325 τA:(a) without radiation, (b) with radiation.
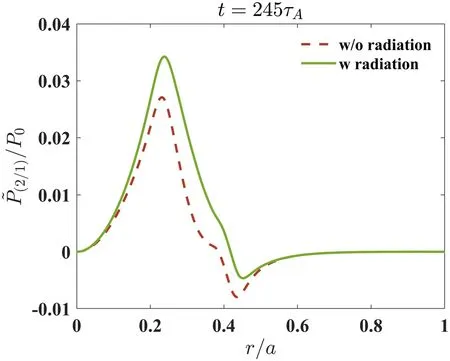
Figure 4.The eigenmode structures of m /n = 2 /1 for the perturbation of pressure with fb = 0.3att =245τ Awith/without radiation.
The temporal evolution of the magnetic island width of differentfbvalues with and without radiation is shown in figure 6.For the case without radiation, the raise of the bootstrap current perturbation leads to the increase of the magnetic island growth rate, and the width of saturated magnetic islands also increases.Furthermore, the larger the bootstrap current fraction is, the earlier the magnetic island width reaches saturation.However,with the plasma radiation,the magnetic islands keep growing in the nonlinear phase and do not saturate which indicates that the NTM instability can be further promoted by the plasma radiation.As shown in figure 5, the perturbation of bootstrap current inside the magnetic islands increases, which promotes a gradual increase of the magnetic island width under the action of plasma radiation.Therefore, it is found that the radiation can keep destabilizing the NTMs through increasing the magnetic island width in tokamak plasmas.
The above numerical simulation results show that the plasma radiation can destabilize the NTMs.In addition, such a result can be further explained by the theoretical analysis.White et al modified the Rutherford equation comprehensively in [40]:
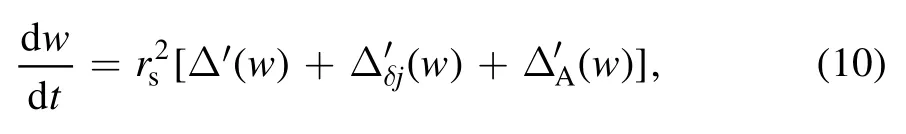
wherewandrsare the width of the magnetic islands and the position of rational surface in the radial direction, respectively.Δ′(w),andare the classical effects, the current perturbation effects caused by neo-classical or other current perturbation effects, the island asymmetry effect,respectively.Here
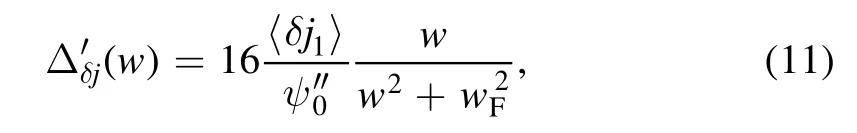
wherewFis the Fitzpatrick’s critical island width.The bracket indicates integrating over the island interior, andδj1is the perturbation of current.As a result, the raise of the perturbation of bootstrap current,leading to the enhancement of the closed integral of current perturbation over the magnetic islands, can increase the growth rate of the magnetic islands and then broaden the width of the magnetic islands.
3.2.Effects of χ‖ /χ⊥with radiation
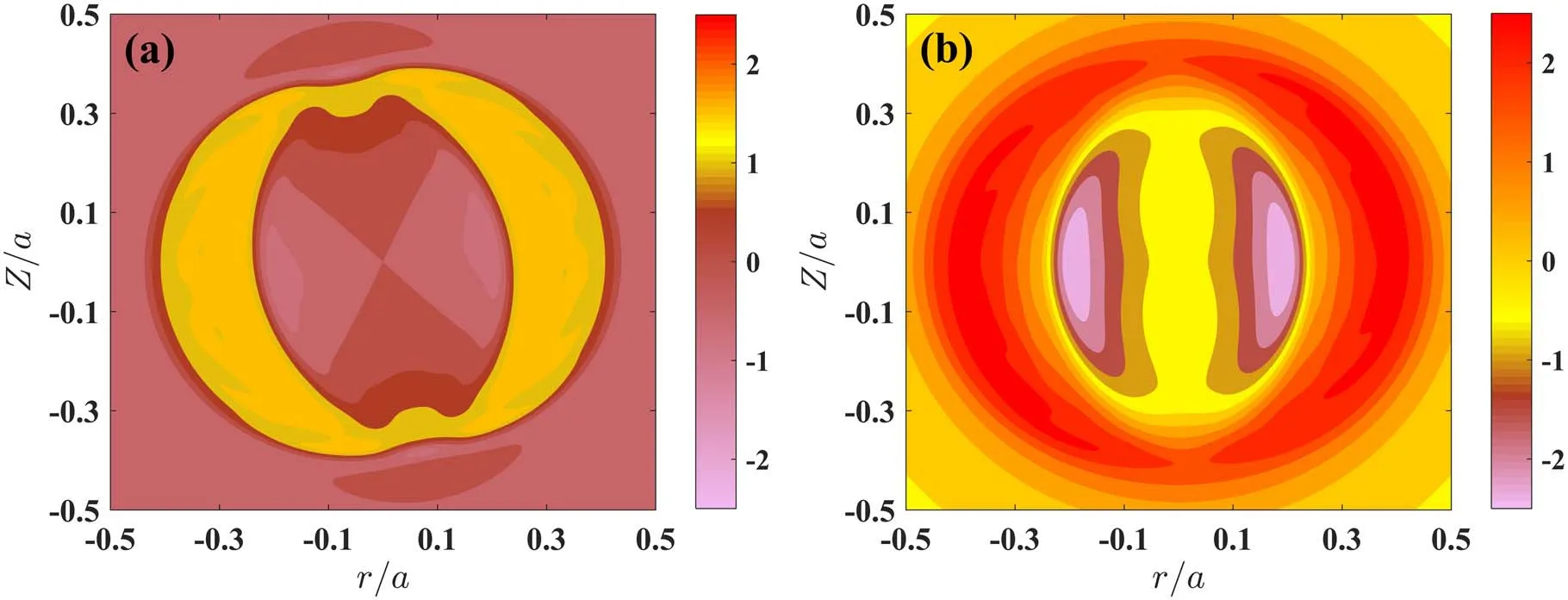
Figure 5.Typical contours of m /n = 2 /1for the perturbation of bootstrap current with fb = 0.3att = 325 τA:(a)without radiation,(b)with radiation.

Figure 6.Temporal evolution of magnetic island width under fb = 0.1,0.2 and 0.3 with/without radiation.
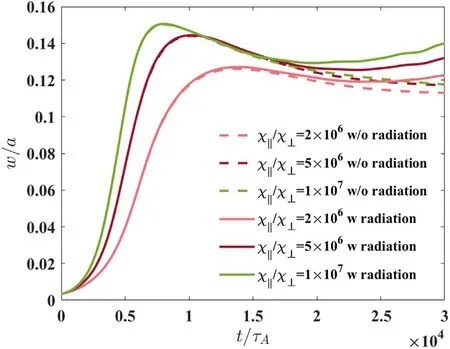
Figure 7.Temporal evolution of magnetic island width with= 2 ×10 6,5 × 106and 1 × 107at fb = 0.3with/without radiation.
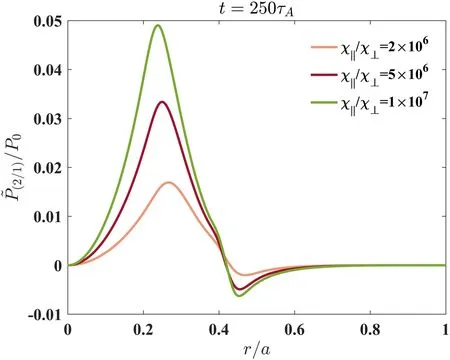
Figure 8.The eigenmode structures of m /n = 2 /1 for the perturbation of pressure= 2 ×10 6,5 × 106and 1 × 107at fb = 0.3,t =250τ A with radiation.
This section presents the influence of the heat transport coefficients on the NTMs with the plasma radiation.There is no doubt that the energy confinement time in tokamak is inversely proportional to the heat transport coefficients, so it is significantly important in the field of magnetic confinement to further understand the physical mechanism of the heat transport coefficients in the presence of the plasma radiation.It can be found that the growth rate of the magnetic islands decreases with the decline of the ratioin figure 7 whether there is radiation or not.For the case without radiation,the raise of the ratiocan lead to the growth of the magnetic islands and eventually the width of magnetic islands tends to saturate.However, the magnetic islands do not saturate due to the existence of the radiation,but keep in a growing state.As shown in figure 8, the magnitude of eigenmode structures for the perturbation of pressure increases with the increase of the ratioby taking= 2 ×106,5 × 106and 1 × 107atfb= 0.3in the presence of the plasma radiation.Furthermore, the influence of the parallel thermal transport termon the NTMs is destabilizing, whereas that of perpendicular termis opposite, as indicated in equation(3).As seen from figures 7 and 8, when the ratio of parallel to perpendicular transport coefficient,is large, the pressure inside the magnetic islands is lower than that outside the magnetic islands,which causes the increase of pressure perturbation and then the incessant growth of the magnetic islands.Accordingly,simulations show that the presence of the radiation can still enhance the destabilizing effects of the increase ofon NTMs.
4.Summary and discussions
The numerical results reported in this work reveal the effects of the radiation on the NTMs, based on a set of reduced MHD equations.The main results can be summarized as follows.First of all, the plasma radiation can reduce the pressure near the rational surface,resulting in the increase of the perturbation of pressure inside the magnetic islands, such that the plasma pressure forms a concave structure.Particularly, the effects of radiation can lead to the increase of the perturbation of bootstrap current inside the magnetic islands, so that the magnetic islands do not saturate and keep growing.In addition, the perturbation of pressure can also be enhanced and then the magnetic islands are destabilized by increasing the ratio ofin the presence of the plasma radiation.Consequently, the effects of plasma radiation can greatly destabilize the NTMs.In experiments, the electron cyclotron current drive (ECCD)can compensate the loss of the bootstrap current thus it is usually used to suppress the NTM islands.When the effects of plasma radiation on NTMs are taken into account, the effectiveness of ECCD may be weakened.These effects will be investigated in our future work.
Acknowledgments
The authors thank Dr Huishan CAI for stimulating discussions on this work.This work is supported by the National Magnetic Confinement Fusion Energy R&D Program of China (Nos.2019YFE03090300 and 2017YFE0301100), National Natural Science Foundation of China (Nos.11925501 and 12075048),the Fundamental Research Funds for the Central Universities(Nos.DUT21GJ204 and DUT21LK28).
ORCID iDs
猜你喜欢
杂志排行
Plasma Science and Technology的其它文章
- Integrated data analysis on the electron temperature profile of HL-2A with the Bayesian probability inference method
- Prompt acceleration of a μ+ beam in a toroidal wakefield driven by a shaped steeprising-front Laguerre-Gaussian laser pulse
- The influence of weak transverse magnetic field on plasma dissipation process in the post-arc phase in a vacuum interrupter
- Numerical study of the effect of coflow argon jet on a laminar argon thermal plasma jet
- On the green aurora emission of Ar atmospheric pressure plasma
- Dynamic characteristics of multi-arc thermal plasma in four types of electrode configurations
