敏捷卫星动中成像自主任务规划算法

陈雄姿，谢 松，蔡 熙，于灵慧，杨 芳

（航天东方红卫星有限公司，北京 100094）

0 引言

敏捷遥感卫星成像模式主要可分为被动成像和动中成像两种［1-2］。被动成像仅依靠卫星的轨道运动实现对目标区域的推扫成像，成像期间除了偏流角修正外卫星姿态保持不变，获得与星下点轨迹平行的观测条带；由于受太阳同步轨道和载荷幅宽等的限制，这种模式在东西方向的成像覆盖能力较弱。动中成像是一种卫星在成像过程中通过姿态机动实时调整相机视轴对地指向来完成目标覆盖的主动推扫成像方式，其最大的优点在于能实现非沿迹方向成像，即斜条带成像，使卫星在东西方向的成像能力大幅提升，对于边境线、海岸线、河流等狭长弯曲目标的覆盖能力也显著增强。法国的Pleiades卫星［3］最早采用了这种成像模式，中国2021年发射的北京三号卫星［4-5］也实现了单斜条带、斜条带拼接、斜条带拼幅等多种动中成像模式。为了更好地满足用户日益增长的复杂观测任务需求，具备动中成像能力已经成为敏捷对地观测卫星技术发展的重要趋势。

敏捷卫星一般具有很强的三轴姿态机动能力，对地面目标的可见窗口更长，观测窗口的选取更为灵活。敏捷卫星任务规划技术是敏捷卫星对地观测应用中的一项核心技术［2，6-7］，负责在满足卫星使用约束和资源约束的条件下制定出让用户满意的卫星任务执行计划，以期达到最大化卫星获取图像数量和质量的目标。国内外学者从敏捷卫星工作模式、任务规划模型和求解算法等方面开展了大量研究［6-9］。经综合分析可知：首先，超敏捷卫星的动中成像任务规划问题是未来的一个重要研究方向［7］，现有研究成果解决的主要是同轨多点目标成像、区域目标多平行条带拼接成像、多视立体成像等被动成像的任务规划问题，尚未涉及动中成像的任务规划问题；其次，由于在提升卫星应急响应能力、减少对地面测控依赖和支撑多星协同观测等方面具有显著优势，星上自主任务规划已经成为敏捷卫星任务规划技术的一个研究热点［8-9］。理论研究方面：文献［10］设计了星上自主任务规划的模式与框架，提出了一种滚动规划启发式算法；文献［11］建立了敏捷任务规划的数学模型并设计了一种基于分支定界的星上规划求解算法；文献［12］设计了一种兼顾求解速度和结果收益的“逐级择优”在轨任务实时规划算法；文献［13］提出了一种新的基于改进混合整数线性规划的星上任务规划方法；文献［14］使用禁忌遗传模拟混合算法来处理敏捷卫星的自主任务规划问题。工程实践方面：文献［15］介绍了法国航天局研发的星上自主系统在Pleiades卫星上进行的试验验证情况，该自主系统考虑了大部分的敏捷成像约束；文献［5］系统地阐述了北京三号卫星自主任务规划的设计和在轨一年的应用情况，它实现了观测任务和数传任务的星上完全自主一体化规划。上述两颗星均具备动中成像能力，但文献中关于动中成像的模型及解算细节均未详述。

相比于地面任务规划，自主任务规划由于受星上计算能力和存储资源的限制，对使用的模型与算法不仅要求高质量还要求具备高效率。另一方面，与被动成像任务规划相比，动中成像任务规划的求解更为复杂，区别和难点主要表现在：1）需要考虑区域目标斜条带的划分问题；2）动中成像过程中要求实时调整卫星的三轴姿态，对于任务规划来说，需要计算各斜条带起止时刻卫星所需的姿态角、角速度和角加速度，特别是偏流角计算与被动成像存在显著差异；3）由普通任务切换到动中成像任务时或者两个动中成像任务切换时，卫星的姿态角和角速度需要同时预置到位，如何计算相邻任务间所需的最短姿态机动时间也是一个难题；4）由于成像过程中姿态的变化特性，动中成像规划需要更加关注成像质量问题，特别是同一个斜条带拼接组内多个任务的联合编排以及成像质量的优化。

综上所述，敏捷卫星动中成像自主任务规划是一项亟待突破的关键性技术和难点技术。本文针对敏捷卫星动中成像自主任务规划所涉及的关键算法进行了研究，有效解决了区域目标斜条带划分、斜条带动中成像姿态规划、动中成像任务间最短姿态机动时间计算和顾及成像质量的任务优化编排等问题。相关研究成果已经在北京三号卫星上成功验证与应用［4-5］，具有很高的工程应用价值。

1 动中成像自主任务规划问题

1.1 动中成像模式

如图1 所示，动中成像模式主要可分为单斜条带成像、斜条带拼接成像和斜条带拼幅成像三种。斜条带定义为由地球表面任意两点确定的一段过地心的大圆弧（劣弧），斜条带宽度为相机幅宽。单斜条带成像是对与星下点轨迹成任意夹角的一个斜条带进行成像，适用于线目标成像；斜条带拼接成像是多个斜条带首尾衔接成像，该模式适用于观测边境线、河流、海岸线等狭长弯曲的目标。斜条带拼幅成像是利用多个斜条带进行幅宽拼接，一般选择与星下线垂直的斜条带，实现东西方向幅宽较大的区域目标覆盖。

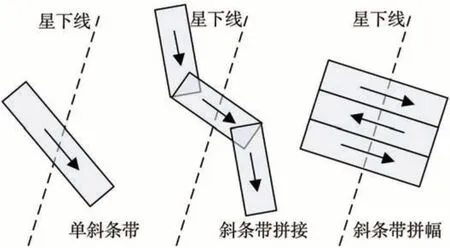
图1 三种动中成像模式Fig.1 Three active push-broom imaging modes

1.2 问题描述

1.2.1 观测任务信息

令{Ai|i=1，2，…，N}表示包含动中成像任务的敏捷对地观测卫星的成像任务序列，N为任务数目，每个任务单独设置了优先级pi和最大观测半锥角Φi两个属性。优先级的取值为1～10 的整数，数值越大优先级越高。最大观测半锥角定义为成像时相机视轴与轨道坐标系+Z轴的夹角。动中成像模式可设置为1.1 节所述的任意一种，其中斜条带拼接任务由多个线目标任务组成，这些目标还需指定统一的拼接组号和表征拼接顺序的组内序号，一个拼接组包含的最大子任务个数为Lmax。

1.2.2 主要约束条件

假设已知敏捷卫星的轨道高度为H，相机在卫星零姿态时星下点的有效观测幅宽为η，卫星绕任意轴转动允许的最大角速度和角加速度分别为

任务规划考虑的约束条件主要包括：

1）若Ai安排观测，则观测角度必须小于其允许的最大观测半锥角Φi；

2）被安排执行观测的相邻两个成像条带间的姿态机动不允许超出卫星的最大姿态机动角速度和角加速度，例如图2中从P1机动到P2、从P3机动到P4。

图2 动中成像观测任务执行示意图Fig.2 Schematic diagram of active push-broom imaging task

对于卫星图像存储、可用能源等一般性约束，本文假设资源充足，不做重点考虑。

1.2.3 优化目标函数

敏捷卫星的自主任务规划本质上是基于有限的星载计算和存储资源在满足规划约束条件下求解指定规划周期范围内的一个优化问题，其目标函数为：

式中：ci是观测任务Ai的收益，xi为系数。若Ai安排观测，xi=1；否则，xi=0。

1.2.4 关键问题分析

完整的自主任务规划流程一般包括：轨道预报、任务预处理、任务优化调度等步骤［5］。与被动成像相比，动中成像任务规划需要解决一些新的问题。

任务预处理阶段，动中成像任务的轨道圈次分配和可见窗口计算与被动成像任务的处理方法基本一致，但元任务分解的差异较大，单个线目标只需用连接目标两端的一个斜条带即可覆盖，关键是要解决如何将幅宽较大的斜条带拼幅区域目标划分为多个垂轨斜条带。

任务优化调度阶段，动中成像任务的特殊性主要是成像过程中需要实时调整卫星三轴姿态，姿态角和角速度均要符合指定要求。首先，需要计算各斜条带任意指定成像窗口起止时刻（例如图2 中的P1、P2、P3和P4）卫星所需的姿态角、角速度和角加速度，作为计算相邻任务间姿态切换时间的依据；其次，为了实现在指定时刻对姿态、角速度的建立和确保姿态平稳过渡从而避免引起挠性模态振动，动中成像任务间的姿态规划一般采用多项式规划方法［16］；为了最大化编排任务的数量，需要研究在卫星姿态机动能力范围内求解任务间最短多项式姿态机动时间的方法；另外，考虑到动中成像任务姿态的动态变化特性和同一个斜条带拼接组内多个任务的联合编排要求，式（1）中的观测任务收益ci需特别考虑成像质量因素，增加成像质量的优化。

因此，本文后续内容针对上述动中成像自主任务规划的几个关键问题，分别设计了星载处理器可用的处理算法。

2 区域目标斜条带拼幅垂轨条带划分

已知区域目标m(m＞2)个边界顶点的地理经度和纬度的集合假设在任务预处理阶段，经目标可见性分析已经将该目标分配到了合理的卫星轨道圈次，垂轨斜条带划分步骤如下。

计算区域目标中心的地心距Rc。使用式（2）计算各边界顶点的地固系矢量ri，则Rc取各矢量长度的均值。

垂轨条带成像幅宽受成像姿态影响，在成像过程中条带幅宽是动态变化的。由于目标的最终观测时间尚未确定，为了能够确保目标在可用观测窗口内任意时刻执行观测均能实现完全覆盖，采用卫星零姿态星下点有效幅宽η进行垂轨条带的划分，区域目标所需要划分的垂轨斜条带数：

进一步基于起止点的正侧视信息可以求出条带起止点的地理经纬度(λ1，δ2)k和(λ2，δ2)k［17］。如图3所示，当选择正反推扫结合时，按一正一反交替分配，对于反扫条带，条带起止点需要交换位置。

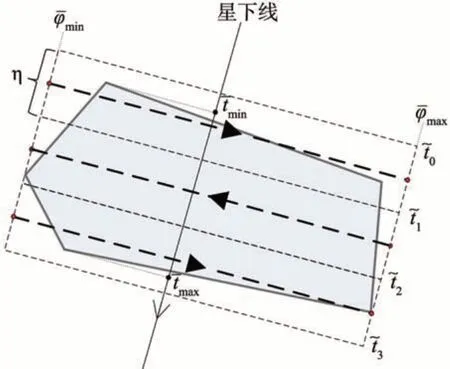
图3 区域目标垂轨条带划分示意图Fig.3 Non-parallel strip division for area target

3 动中成像姿态计算

文献［18-19］提出了一种敏捷卫星动中成像的姿态调整方法，该方法仅适用于东西方向成像，且假设地球为理想球体以及卫星轨道面为一个绝对平面，与工程实际不相符。本节提出一种更加简单有效的斜条带成像姿态规划方法。

3.1 斜条带成像轨迹模型

如图4所示，O -xeyeze为地固坐标系，A、B 分别为斜条带的起点和终点，且已知它们的地理经纬度分别为（λ1，δ1）和（λ2，δ2）。

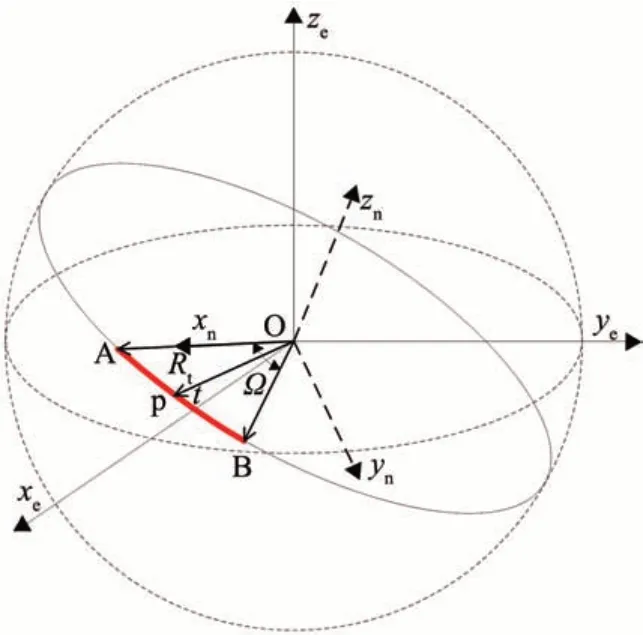
图4 斜条带成像轨迹模型示意图Fig.4 Imaging trajectory model of non-parallel strip

基于式（2）可得到A、B 两点在地固系的位置矢量(rA)e和(rB)e，它们的长度分别为rA和rB。

(rA)e和(rB)e之间的夹角为

为了保证地物点运动速度的一致性，相机视轴（一般为星体+Zb轴）所指向地面目标点P 对应的地心矢量在OAB 平面内的转动角速度是均匀的。假设转动角速度大小为卫星轨道角速度ωs的k倍（k可取0.8～1.2），则成像总时长：

于是，t(0 ≤t≤T)时刻P 点在地固系下的位置矢量(Pt)e与(rA)e的夹角为由于地球为椭球体，Pt的长度Rt在成像过程中是缓慢变化的，考虑到斜条带长度相对于地球周长是小量且任务规划只需关注斜条带起始和结束时刻卫星的姿态信息，这里使用线性插值来简化计算：

如图4所示，建立一个新坐标系O -xnynzn，xn轴沿(rA)e方向，zn轴沿(rC)e=(rA)e×(rB)e方向，yn轴符合右手法则。A、B 两点在该坐标系的位置矢量分别为

令(rA)e，(rB)e和(rC)e三个矢量组成矩阵E的三列，E=[(rA)e(rB)e(rC)e]；令(rA)n，(rB)n和(rC)n三个矢量组成矩阵N的三列，N=[(rA)n(rB)n(rC)n]，其中(rC)n=(rA)n×(rB)n。则O -xnynzn坐标系与地固系的转换矩阵Aen为

因此，t(0 ≤t≤T)时刻P 点在地固系下的位置矢量可以表示为

3.2 三轴姿态计算

根据敏捷光学遥感卫星成像原理，可以建立如图5 所示的斜条带成像几何模型：卫星的轨道坐标系为S-XoYoZo，S 为卫星的质心，Zo轴指向地心，Xo轴指向飞行方向，Yo由右手定则确定，星下点为S′，P为成像t时刻卫星需要拍摄的斜条带上的点。假设相机视轴与卫星本体系的+Zb轴重合，像平面的x轴和y轴分别与卫星本体系的Xb轴和Yb轴平行。零姿态时卫星本体坐标系与轨道坐标系重合，采用1-2-3姿态转序。

图5 敏捷卫星斜条带成像几何模型Fig.5 Geometric model of active push-broom imaging

基于式（9）可计算出成像任意t时刻观测点P在地固系下的位置矢量(Pt)e，已知该时刻卫星S 在惯性坐标下的位置矢量为r，地固系到惯性系转换矩阵Aie，惯性系到轨道系的转换矩阵Aoi。

轨道坐标系中卫星S指向观测点P的矢量为

则卫星的滚动姿态角φ和俯仰姿态角θ分别为

偏航角不影响对地指向，但线阵推扫成像需要实时调整偏航角进行像移补偿，以保证线阵推扫方向与目标像移方向一致。由于点P相对于像平面的移动速度Vb与卫星本体角速度ωb存在耦合关系［20］，并且任务规划是提前完成的，无法通过惯性敏感器实时获取ωb来计算偏流角。考虑到描述观测点在地固系下的位置坐标x，y，z与成像时间t之间关系的式（9）连续可导，因此，任意t(0 ≤t≤T)时刻地固系下地面观测点的滑动速度可表示为

其中，Abo为卫星滚动和俯仰机动后轨道坐标系到本体系的姿态矩阵。

于是，正向推扫时卫星偏航角计算公式为

反向推扫时卫星偏航角计算公式为

ϕ的取值范围为(-π，π]。在成像起始和结束时刻，通过取微小时间步长（例如0.01 s）做差分可得到三轴角速度和角加速度的值。

4 任务间最短姿态机动时间求解

本节基于六阶多项式的姿态机动轨迹规划方法［16］，提出了任务规划中动中成像任务间最短姿态机动时间的求解算法。

4.1 多项式姿态机动轨迹规划

假设卫星机动起始时刻和结束时刻的姿态角、角速度和角加速度信息分别为和，并假设两点之间姿态机动时间为tm。

六阶多项式姿态轨迹规划模型可以表示为βt=是多项式的系数。根据卫星姿态机动起始时刻的姿态角、角速度和角加速度可确定姿态机动轨迹第一至第三个约束方程为

为了保证姿态机动的平稳性，选取姿态机动结束时刻的角加速度的导数=0作为第四个约束方程；同时，根据卫星姿态机动结束时刻的姿态角、角速度和角加速度确定姿态机动轨迹的第五至第七个约束方程，可解得：

因此，六阶多项式姿态轨迹规划模型为

上面给出的是单通道的规划方法，滚动、俯仰和偏航需要按照该方法进行独立规划。

4.2 最短姿态机动时间解算

两个前后相邻的动中成像任务1 和2，任务1的观测结束时刻确定为t1，任务2 的观测起始时刻为t2且t2可变。由式（11）和式（14）或（15）可分别计算两个时刻卫星的姿态姿态机动时间tm=t2-t1。已知卫星姿态机动的最大角速度和角加速度分别为，为了尽可能多的编排任务，需要求解两点之间最短的姿态机动时间(tm)min。

对于给定的t2，基于式（16）可得到卫星滚动、俯仰和偏航的六阶多项式姿态机动模型，它们的多项式系数分别用a、b和c表示，则t(0 ≤t≤tm)时刻三个通道的角速度和角加速度的值为

卫星姿态机动采用1-2-3转序，卫星本体角速度ω和角加速度a的计算公式分别为式（19）和（20）［17］：

则三轴合成的角速度平方值W(t)和角加速度平方值A(t)分别为：

令g(t)=maxA(t)max分别表示W(t)与A(t)的最大值。因此，计算最小姿态机动时间(tm)min就是求解非线性方程g(t)=0的根。该方程仅有单根，可通过对分法迭代求解，搜索区间为(0，Tm]，Tm为任意两个动中成像任务间的最大姿态机动时间。

5 观测效率与质量两级任务优化调度

敏捷卫星对地成像任务规划算法理论研究成果较多［7］，主要可分为确定性算法［11，13］、启发式算法［10，12］和元启发式算法［14，21］三类，这些算法在不同的应用场景下各有优劣。星上自主任务规划要求高时效性和高可靠性，规划算法应具有效率高、开销小和稳定收敛的特点。为了尽可能多安排观测任务，同时最大程度提升成像质量，提出了一种“及早观测搜索+最佳窗口平移”的两级成像任务优化调度策略。

将式（1）中的第i个观测任务的收益ci定义为

式中：任务优先级pi是观测任务满足其指定最大观测半锥角Φi要求的基础收益，取值为1～10 的整数为图像质量收益为观测任务成像起始时刻和结束时刻的观测半锥角最大值，εi取值范围为越小收益越大。第一级任务优化调度采用分支定界算法搜索满足观测任务指定最大观测半锥角要求的基础观测收益累加和最大化的任务序列；第二级任务调度在第一级调度结果基础上，进一步优化每个编排任务的图像质量收益，实现式（1）中的总收益目标函数值最大。

考虑到观测任务调度在卫星的各个轨道圈之间具有较好的独立性，当规划周期包含多个轨道圈时，上述任务调度在各个轨道圈单独执行。假设轨道圈内经过任务预处理后得到的待观测任务集合为，其中为任务满足指定最大观测半锥角要求的可用观测窗口的起始和结束时刻为任务最佳观测窗口的起始和结束时刻，最佳观测窗口这里定义为和具有相等的观测半锥角。

5.1 基于分支定界算法的及早观测搜索

5.1.1 构造二叉搜索树

依据所有任务可用观测窗口的起始时刻tws进行升序排序，构造二叉搜索树，如图6所示。排序过程中，每一个斜条带拼接组需作为一个整体考虑，组内顺序不变，用组内第一个斜条带的tws参与排序。对于每个任务，规划算法有“观测”和“放弃”两种选择，对应式（1）中的系数xi，左节点xi=1 表示“安排”，右节点xi=0 表示“放弃”。树的根节点为虚节点，表示卫星初始的姿态和载荷状态，根节点的子节点对应第一个观测任务。

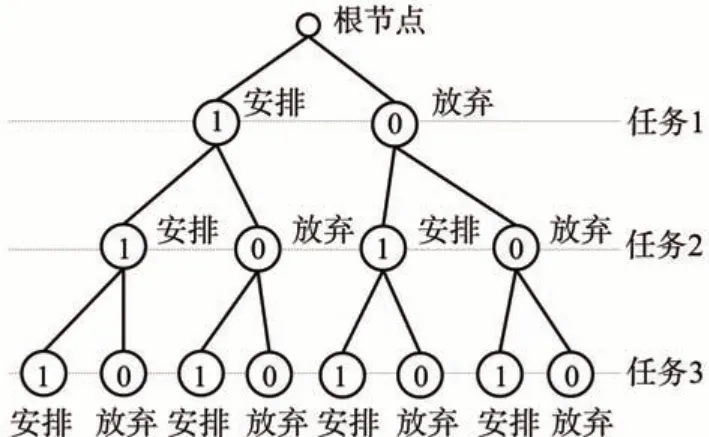
图6 观测任务序列二叉搜索树（3个观测任务示例）Fig.6 Observation task sequence binary search tree（3 observation tasks for example）

搜索树节点的参数主要包括：1）对应观测任务；2）对应搜索路径；3）已达成收益ppre，按照从根节点到当前节点已“安排”观测任务的优先级之和统计；4）剩余任务收益prem，按照从下一个任务到最后一个任务的优先级之和统计。

如果一棵树中有N个观测任务，即树的深度为N，在完全搜索的情况下，需要搜索2N条完整路径，访问2N+1-1个节点。例如图6中，3个观测任务有8条搜索路径，15 个节点。完全搜索优点是可以获得全局最优解，但是计算量会随N呈指数增长。为了满足星载计算能力要求，制定如下构造树的规则。

规则1：考虑任务间的独立性，当相邻的两个任务观测窗口相差超过卫星最大的任务间切换时间Tc时，新构建一棵树，将后一个任务作为新树的第一个节点。

规则2：当一棵树的深度达到设定允许的最大深度Nmax（Nmax≥Lmax）时，将后续的任务安排到一棵新的树，严格限制了每棵搜索树的最大深度。

规则3：属于同一个斜条带拼接组的任务须安排在同一棵树中，同时避免规则2 将同一个斜条带拼接组的任务拆分到两棵树。

只触发规则1时，全局规划结果仍是最优解；当触发规则2 或规则3 时，每棵树的规划结果为最优解，全局为较优解。所有树的总搜索路径个数为：为树的个数，Nk为第k棵树的深度。

5.1.2 深度优先搜索

为了给分支定界算法尽早提供一个较高的下界从而大大加快搜索速度，对二叉树采用深度优先先序遍历搜索。第k(1 ≤k≤M)棵树的搜索步骤如下：

1）初始化下界Blow=0。

2）初始化虚节点的卫星状态。当k=1时，虚节点为空闲状态；当k＞1，虚节点状态为第k-1 棵树安排的最后一个观测任务观测执行完毕对应的时刻和卫星姿态。

3）采用深度优先搜索算法遍历搜索树。

从树的顶部开始往下搜索，对搜索路径中的每一个任务节点做如下处理：当节点已“安排”观测时，计算该节点的已达成收益ppre和剩余任务收益prem，在保证与前面紧邻的安排任务可正常切换的前提下，选择最早的观测窗口，为后续任务留出更多的时间；同时使用收益预测裁剪规则和时序冲突裁剪规则对搜索树剪枝，以缩小搜索空间、加快搜索速度。

收益预测裁剪规则：若ppre+prem≤Blow，即当前节点后续所有分支路径的上界不超出最佳收益的下界时，包含当前节点的路径不是最优路径，裁剪该节点及其左右子树。

时序冲突裁剪规则：若在卫星姿态机动能力范围内，后一个节点任务无法“安排”，即存在时序冲突时，则裁剪该节点任务的左子树。

每一次搜索到树的底部节点时，若有ppre＞Blow，则将当前路径保存为最优路径，并更新下界Blow=ppre。

4）搜索完成，确定最优成像任务序列。令k←k+1，若k≤M，跳回到第1步。

综上所述，所提任务调度算法的主要优点在于：1）通过限制单棵搜索树的最大深度并采用深度优先先序遍历搜索策略和两种裁剪枝规则，能够有效缩小寻优空间，满足在轨应用需求；2）能够获得稳定收敛的优化结果，便于地面平行复现。该方法的不足之处是多数情况下只能得到局部最优解。

5.2 观测队列最佳窗口倒序平移

如图7 所示，为了确保平移不影响任务的可执行性，从安排任务序列的最后一个开始倒序逐个平移，平移步骤如下：

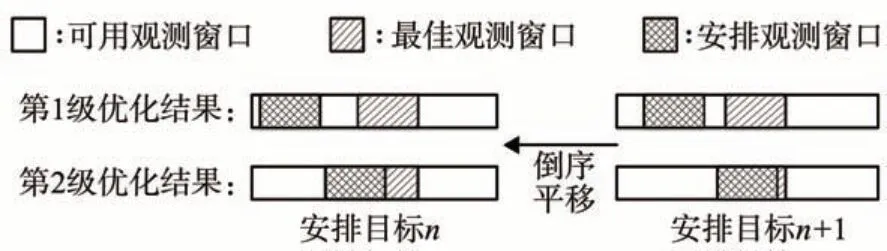
图7 最佳窗口平移示意图Fig.7 Schematic diagram of optimal window translation

1）基于后一个任务平移后的观测起始时间和姿态计算当前任务在[tws，twe]范围内允许的最晚成像起始时间tos_latest，满足tos_latest≥tos；

2）如果tos_latest≤tbws且tos＜tbws，向后平移，取tos=tos_latest；如果tos_latest＞tbws且tos＜tbws，向后平移，取tos=tbws；其它情况，不平移。

6 仿真校验

设计的仿真任务场景主要由一颗500 km 高度的太阳同步轨道敏捷卫星和16 个观测目标组成。卫星的相机视场角2.635°，星下点的有效观测幅宽为22 km，最大姿态机动角速度为6（°）∕s，最大姿态机动角加速度为3（°）∕s2。观测目标包括14 个线目标和2 个区域目标，其位置、优先级、拼接组号和组内序号等信息如表1 所示，线目标包含3 个斜条带拼接组，区域目标用4个边界点描述，均采用正反扫方式。所有目标的指定最大观测半锥角均设为45°，推扫速度均为1 倍轨道角速度。仿真硬件使用星载FT-6701 DSP 处理器，工作频率120 MHz，浮点运算能力960MFLOPS，配备4 MB的外部SRAM。

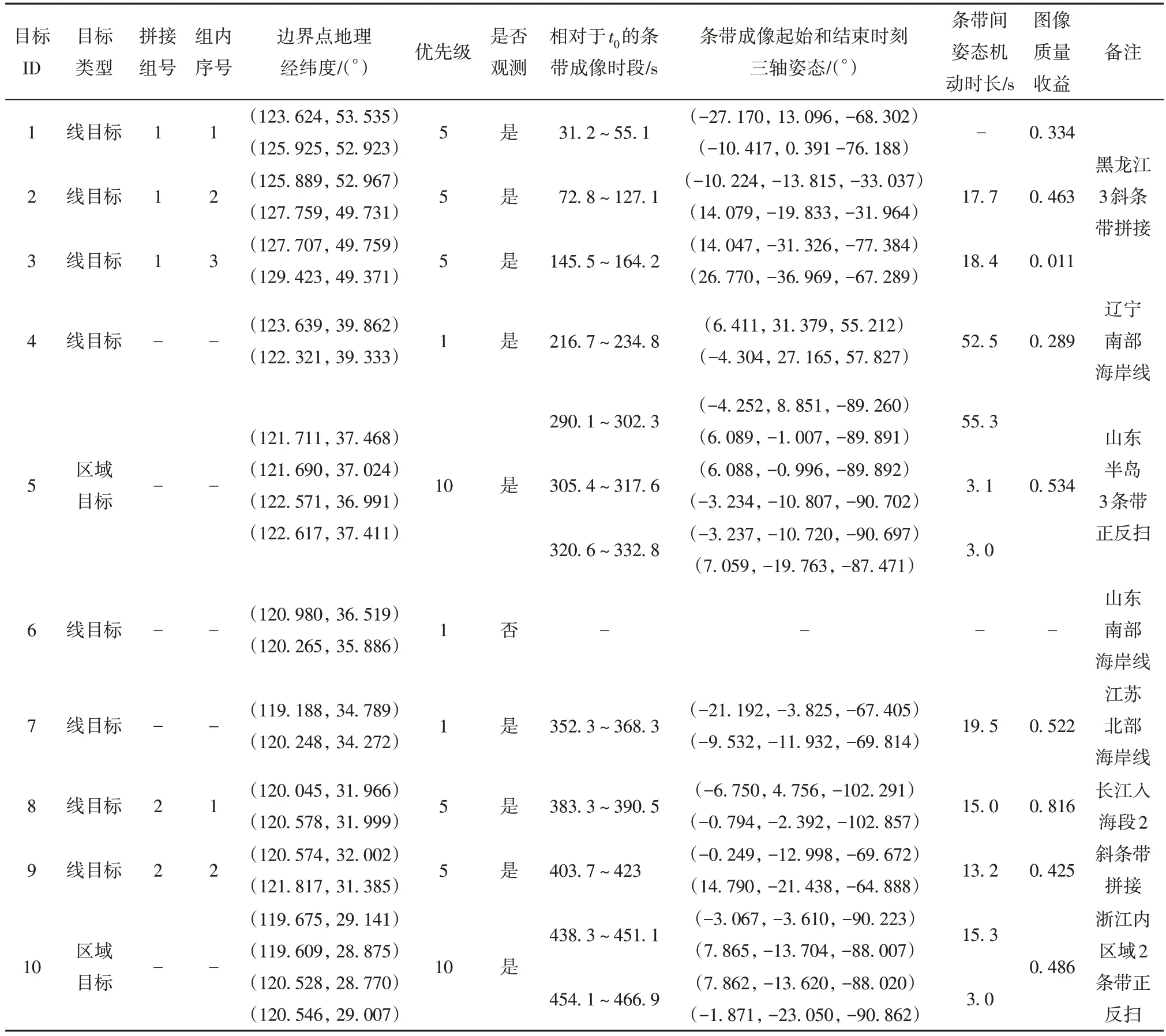
表1 任务信息与任务规划结果Table 1 Task information and task planning results

任务场景的起始时刻t0为北京时间2021年6月23 日9 点59 分，此刻卫星的J2000 瞬时轨道参数为：半长轴6 867.256 km，偏心率0.000 369，轨道倾角97.411°，升交点赤经238.538°，近地点幅角285.038°，平近点角198.288°。规划窗口起始时刻为t0-1 200 s，规划窗口长度设为7 200 s，搜索树的最大深度设为10，任务间的最大机动时间Tm和最大切换时间Tc均设为60 s，规划结果的时间颗粒度为0.1 s。

任务规划仿真计算的结果见表1和图8～图11。

图8 整个任务场景的卫星姿态信息Fig.8 Satellite attitude information for the entire task scenario

由表1 可知，除了目标6、11 和12 由于任务冲突未能安排观测外，剩余的13 个目标均安排观测，区域目标5 划分了3 个斜条带，区域目标10 划分了2 个斜条带。表1 给出了全部16 个条带的规划结果，包括成像起止时刻、成像起止时刻卫星三轴姿态、条带间的姿态机动时间和图像质量收益等。

整个规划计算（含轨道预报和任务预处理）用时45.1 s，16 个目标构造了两棵搜索树。第1 棵树为目标1～10，深度为10，搜索完整分支4 条（总共1 024 条），访问节点44 个（总共2 047 个），安排观测目标9个，总的基础收益为47，总的图像质量收益为3.88。第2 棵树，深度为6，搜索完整分支10 条（总共64 条），访问节点47 个（总共127个），安排观测目标4个，总的基础收益为20，总的质量收益为1.136。可见，设计的收益预测裁剪规则和时序冲突裁剪规则大幅裁剪了搜索路径，有效提升了计算效率。

图8（a）给出了整个任务场景卫星三轴姿态的变化曲线，图中曲线加粗部分对应于各个条带的成像过程，可以看出动中成像的偏航角变化范围较大，最大值为57.827°，最小值为-102.857°。图8（b）和图8（c）分别给出了星体合成角速度曲线和角加速度曲线，可见每两个目标间的姿态机动合成角速度最大值均达到了卫星机动能力阈值6（°）∕s，而区域目标内部正反扫条带间的姿态切换由于姿态前后变化较小，触发的是卫星3（°）∕s2的角加速度约束。上述结果表明任务规划发挥出了卫星的最大姿态机动能力，证明了本文所提任务间最短姿态机动时间求解算法的正确性。

图9 给出了任务规划结果执行效果的整体视图，可以看出所有目标都准确覆盖。图10和图11分别是斜条带拼接组1 和区域目标5 的规划结果执行效果局部视图。从图10可以看出，成像时段内相机视轴在地表的滑动轨迹与线目标地表弧段完全吻合，证明了动中成像三轴姿态计算模型的正确性。在图11 中，正扫+反扫+正扫的3 个条带搭接合理，共同实现了对区域目标5 的准确覆盖，证明了本文所提区域目标斜条带拼幅条带划分算法的正确性。

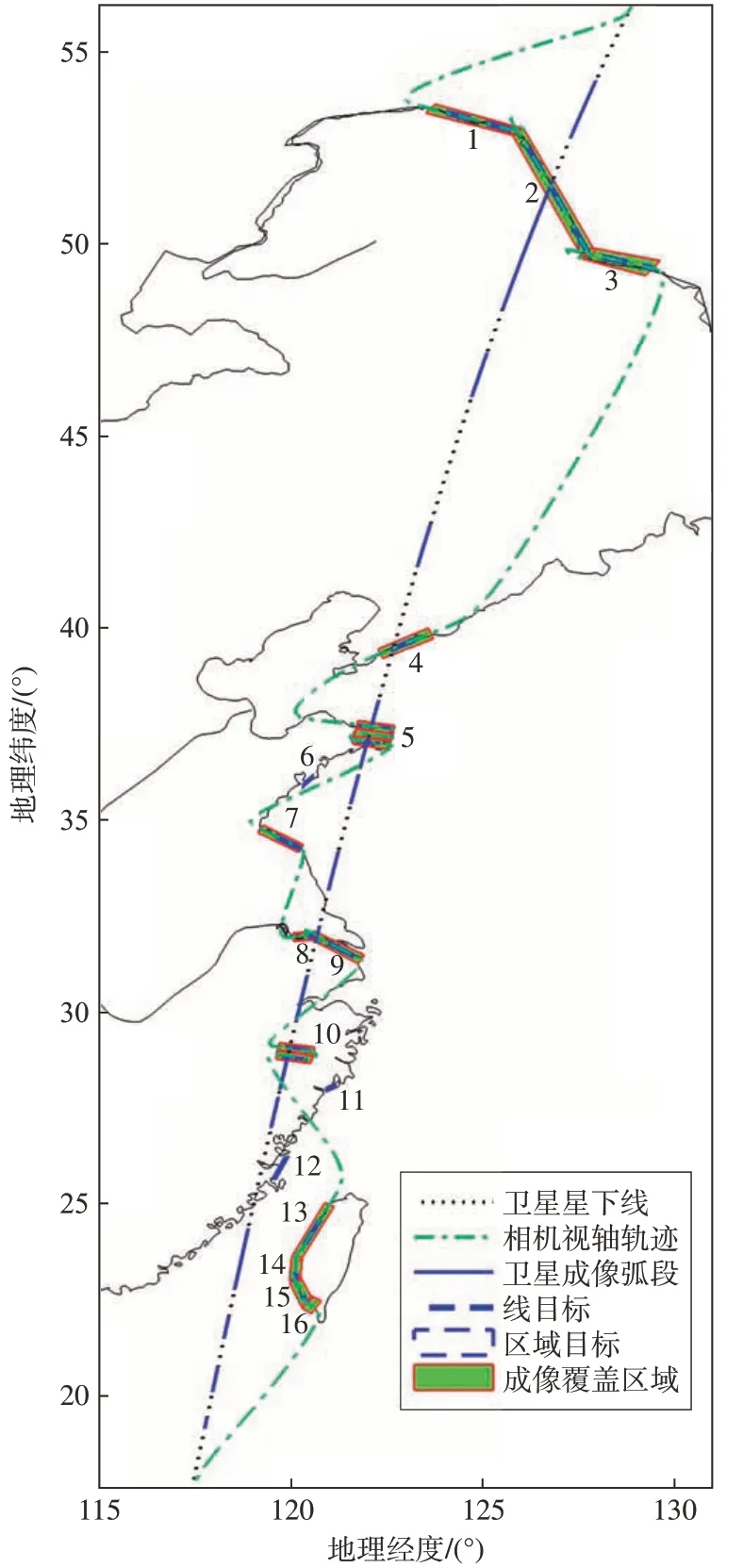
图9 任务规划结果执行效果整体视图Fig.9 Overall view of task planning results

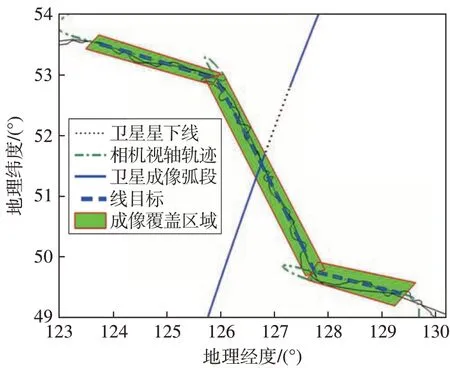
图10 斜条带拼接组1规划结果执行效果图Fig.10 Observation results of non-parallel strip group 1

图11 区域目标5规划结果执行效果图Fig.11 Observation results of area target 5

基于前面的分析可知，由于16个任务分布很紧密，即使发挥出卫星最大的姿态机动能力，仍有3个目标因为任务冲突没有安排观测，此次规划过程中第一级观测效率任务优化调度后大部分目标的观测窗口被安排到了它们的最佳观测窗口之后，第二级观测质量任务优化调度的效果并不明显。为了更好地验证第二级优化调度，只保留区域目标5 和斜条带拼接组3 的4 个线目标，其它仿真设置不变，执行第二次任务规划仿真，结果见图12。

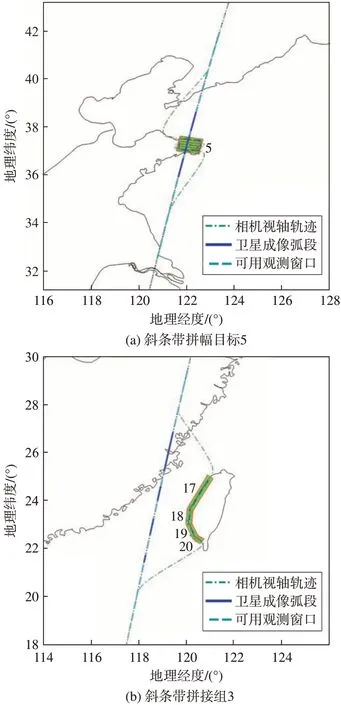
图12 第二次任务规划结果执行效果图Fig.12 Task planning results of the second simulation

如图12 所示，由于区域目标5 和斜条带拼接组3 相互不影响，经过第二级任务优化调度，两项任务都安排到了它们的最佳观测窗口。目标5的可用观测窗口为［228.4 s，379.4 s］，安排的观测窗口为［282.7 s，322.4 s］，起止时刻的观测半锥角均为15.59°，质量收益0.654，较前面仿真结果提升了0.12；斜条带拼接组3 的4 个线目标作为整体考虑，可用观测窗口为［425.6 s，599.2 s］，安排的观测窗口为［469.2 s，554.5 s］，两个窗口的中心点相差0.55 s（设定偏差小于1 s 结束平移），图像质量收益分别是0.396、0.576、0.518和0.375，总图像质量收益相比前面仿真结果提升了0.729。上述结果表明，第二级任务优化调度是非常有效的，观测窗口都平移到了最佳观测窗口的位置，图像质量得到显著改善。

7 结论

针对敏捷卫星动中成像自主任务规划中的几个关键问题，本文提出了4种处理算法：1）区域目标斜条带拼幅垂轨条带划分算法；2）基于斜条带成像轨迹模型的动中成像三轴姿态计算方法；3）基于六阶多项式姿态机动模型的动中成像任务间最短姿态机动时间求解算法；4）兼顾观测效率与成像质量的两级成像任务优化调度算法。在星载处理器上完成的仿真实例中，区域目标被划分的多个斜条带准确完整地覆盖，动中成像姿态下相机视轴指向精准无误，任务间的切换充分发挥出了卫星的最大姿态机动能力，规划结果在最大化观测目标数量的基础上将动中成像任务的成像质量调整到最佳，整个规划运算用时也在可接受的范围内，证明了所提算法的正确性和有效性，具有很高的工程应用价值。