采用注意力模型的多星交会序列优化方法

严冰，张 进，罗亚中，朱阅訸

（1.国防科技大学空天科学学院，长沙 410073；2.空天任务智能规划与仿真湖南省重点实验室，长沙 410073）

0 引言

多目标交会任务要求航天器连续访问多个目标，在主动碎片清除［1-3］、在轨燃料加注［4-6］等任务中具有广阔的应用前景。基于智能进化算法的单航天器对多目标交会任务能够获得较优的序列解，但缺点是计算时间较长，不适合作为多航天器对多目标交会序列问题的底层支撑，亟需发展一种从随机次序输入到最优序列输出的快速估计方法。

大规模多星交会任务优化含有三层优化子问题，分别是上层的多对多分组指派优化、中层的单对多序列优化以及底层的单对单轨迹优化［7］。每层优化都可基于智能进化算法获得较优解，但当相邻两层或三层均采用计算量较大的全局优化算法时，这种嵌套的优化会使得整体计算效率极低。

中层的多星交会序列优化是时间相关的旅行商问题（Traveling salesman problem，TSP），离散序列变量和连续时间变量引入的混合整数特性增加了优化难度。蒙特卡洛树搜索［8］和波束搜索［9］等启发式搜索方法在深空多小行星探测任务优化中取得较好效果。Zhang 等［10］采用混合遗传算法求解近地空间LEO目标的在轨加注优化问题。朱阅訸［7］将蚁群算法（Ant colony optimization，ACO）的信息素矩阵扩展成带时间信息的4 维张量，先全局优化获得较优的序列和时刻后，再通过局部搜索方法进一步优化连续时间变量。黄岸毅等［11］建立的多星多约束遍历交会的混合整数规划模型，获得了性能指标优于第9届国际空间轨道设计大赛［12］（GTOC9）冠军结果的方案。然而现有方法尚未解决分组与序列的嵌套优化，只能在分组指派时借助启发式规则贪婪地获取组内序列，并进行局部修剪［13］。

事实上，具有“离线训练、在线决策”特点的强化学习方法已广泛应用于仅含有离散变量的组合优化问题（Combinatorial optimization problem，COP）中，这是因为强化学习的动作策略选择特点符合COP 的离散决策特性［14］。因此借助神经网络对多星交会问题进行最优序列估计，可以与上层优化实现解耦，进而搜索到更加全局的分组结果。

自然语言处理问题中的序列映射模型（Sequence-to-sequence，Seq2Seq）能够将输入文本序列转换成新的文本序列。Vinyals 等［15］提出了指针网络（Pointer network，Ptr-Net），通过输出指向原序列位置的概率将Seq2Seq 模型应用到序列规划任务中，随后使用监督学习对获得局部最优标签值的数据进行学习，但训练结果往往受限于标签值的精度。因此后续学者均采用强化学习（Reinforcement learning，RL）中 的REINFORCE 算 法［16］对Ptr-Net进行训练，所得解的精度优于多种进化算法，且在不少COP 场景中都接近专业求解器［17-18］。传统Seq2Seq 模型基于循环神经网络（Recurrent neutral network，RNN）描述文本之间的时序相关性，在编码过程中文本参数只能被RNN 单元依次读取并生成隐含状态，这种递归结构使得数据无法并行计算，计算效率较低。为此，Vaswani 等［19］提出自注意力机制，仅使用注意力模型描述文本之间的时序关系，实现了输入文本数据的并行处理。这种采用自注意力机制的Seq2Seq 模型，也称为Transformer 模型。Kool等［20］对其进行改进，在TSP、车辆路径问题等任务中的性能表现均超越了基于RNN的Ptr-Net。

目前基于强化学习的多星交会序列优化研究仍处于起步阶段。为此本文搭建了面向多星交会问题的强化学习框架，引入Seq2Seq 模型构成交会序列的策略网络，最后采用基于回合更新的带基线的REINFORCE 算法对网络参数进行更新。多星交会马尔可夫链、策略网络和REINFORCE 算法之间的关系如图1所示。

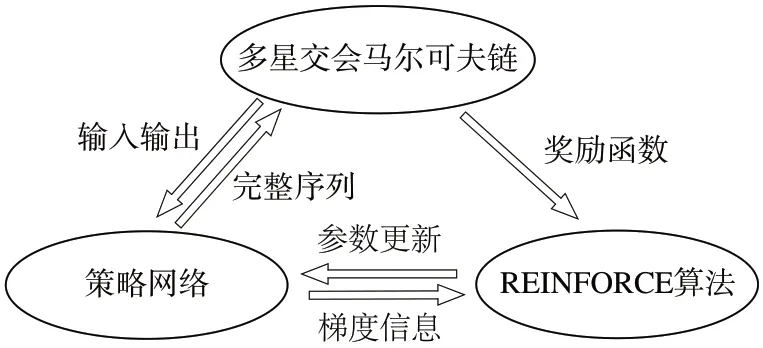
图1 基于强化学习的多星交会基本架构Fig.1 Basic structure of multi-target rendezvous based on RL

1 面向多星交会的强化学习建模

多星序列优化问题在考虑时间维度的前提下，其离散决策属性仍然十分鲜明，即以目标数量n为航天器（智能体）的执行总步长，每次只访问一个目标。智能体在第t步中包含5个要素，分别是状态空间st、动作空间at、即时奖励rt、折扣因子γ和状态更新方程。所有决策过程符合马尔可夫特性，即智能体在下一步的状态只与上一步的状态有关，与其他步的状态无关。

1.1 状态空间

航天器在交会时刻与目标的状态保持一致，因此每一步的状态空间s（tt=1，2，…，n）即为访问目标在对应时刻的位置速度或轨道根数。

1.2 动作空间

智能体的动作既有离散变量（访问目标），又有连续变量（访问时刻），不利于策略网络的学习。可将任务总时长Tmax均匀分成m段，让智能体在不同时间节点下的目标之间进行决策。因此每一步的动作空间at包含访问目标的序号It以及交会时刻的网格序号Tt，表达式为

由于每步决策时动作维度不变，即（m+1）×n，因此需要借助掩码约束，确保目标It未被访问，且前后交会时刻和剩余目标的时间满足基本任务需求，约束表达式为

1.3 即时奖励

在多星交会序列问题中，三维空间的欧式距离无法准确衡量航天器的转移代价，需要借助两两目标之间转移的最优速度增量Δv进行描述。然而，通过轨迹优化获取最优Δv需要较高的计算成本，可采用精度较高的转移成本估计方法。已有研究从轨道动力学模型出发，基于Edelbaum 公式和轨道根数差对二体与摄动条件下的转移成本进行估计［21-23］。此外，利用机器学习方法将成本估计建模成监督学习中的回归问题也是一种有效手段，一般需要结合轨道领域知识提高解的精度［24-25］。为了提高学习效率，摄动条件下的多脉冲最优解可采用文献［22］的方法进行估计。需要注意的是，在论证学习方法的性能优劣时，必须确保其他序列优化方法也采用相同的底层估计算法。

经典TSP 问题采用的REINFORCE 方法是基于回合更新的，因此单步决策没有即时奖励，直接以完整序列的总路径长度为期望（折扣因子γ=1），因此最后一步的奖励rt设为总的转移速度增量。rt表达式为

由于估计算法得到的成本值与考虑了初始和终端脉冲时刻自由的多脉冲轨迹优化结果十分接近，因此动作空间at无需引入航天器完成在轨驻留后的出发时刻。当到达时刻固定时，出发时刻越早，脉冲时刻的搜索范围越大，越有可能得到高质量的速度增量。

1.4 状态更新

智能体的状态转移过程不存在随机性，在更新状态空间st时，要将交会目标It的轨道根数外推至Tt时刻。目标在近地空间除了受到地球引力外，还需要考虑J2长期项摄动影响，轨道动力学方程为

式中：［a，e，i，Ω，ω，M］为平均轨道根数，表示目标的半长轴、偏心率、倾角、升交点赤经、近地点幅角和平近点角。更新完st要将bIt从0置为1。

综上，多星交会任务中的强化学习要素如图2所示，s0为航天器初始状态，通过at可以选择交会目标，并将状态外推至对应时刻，直到最后一步决策对所有的速度增量进行累加作为即时奖励rn。

图2 多星交会任务中的强化学习要素Fig.2 Elements of RL in multi-target rendezvous task

2 基于注意力模型的策略网络搭建

基于Seq2Seq 模型的策略网络π（θat|s）t用于序列输出，在每一步中生成所有候选目标的概率分布并进行随机采样得到当前目标和时刻索引，即为动作at。其流程可分解为编码和解码，θ代指所有的神经网络参数。编码器负责对原始输入数据进行高维映射，转换成隐含状态。解码器则在每一步中结合隐含状态和历史决策选出当前目标，步步推进即可确定一条完整序列。在组合优化问题中，由于输入序列是随机的，注意力模型体现在解码过程中。

2.1 编码器

在机器翻译问题中输入文本的序列会影响输出词汇的序列，因此编码器要将输入文本之间的序列相关性表达出来。而在传统TSP等路径规划问题中，输入序列是随机的，编码器只需要充当嵌入层，将输入参数投影到高维空间。记n个目标的状态向量为x，通过线性映射将其转换为隐含状态h：

式中：x∈Rn×6；神经网络参数Wx∈R6×dh，bx∈Rdh；dh为特征维度。

多星交会问题的决策空间既包含目标也包含时间，要让策略函数选出带时间信息的目标，只有在编码时将所有离散时刻的目标状态都作为输入，才可以让πθ在同一个目标的不同时刻之间作选择，此时x∈Rn×（m+1）×6，h∈Rn×（m+1）×dh。

2.2 解码器

解码器采用自回归模型，每一步解码都会对所有时刻的目标产生注意力，从而输出一个目标It和相应的到达时刻Tt，共执行n步。考虑到Transformer模型在应用于机器翻译问题时，编码器和解码器需要分别使用自注意力机制描述输入和输出序列之间的相关性，而在路径规划问题中编码器无需采用该机制，因此将应用于此类问题的Transformer 模型称为注意力模型。

2.2.1 拓展时间维度的注意力模型

在注意力模型中需要设计一个包含上下文信息的隐含状态hc，由隐含状态h关于所有时刻的目标的平均值，第一步决策的T1时刻的目标以及上一步决策的Tt-1时刻的目标组成［20］。hc的表达式为

用Q与K的内积表示每一步的解码输入hc与编码输出h之间的兼容性，并对不满足约束的目标和时刻的兼容性进行惩罚，使得解码时对该时刻的目标的注意力为0。

式中：uj，k，l表示第l个头的解码输入与目标j在时刻k的兼容性；j=1，2，…，n；k=0，1，…，m；l=1，2，…，L。将j和k取代式中的It和Tt，即可确定满足掩码约束的取值范围。

将兼容性经过归一化指数函数（softmax）处理后得到权重张量，即相对于某个目标和时刻的注意力程度。其中第l个头的目标j在时刻k的权重为

2.2.2 结合启发因子的概率分布

在多星交会任务中时间网格是稀疏的，注意力难以集中在关键的交会时刻上，从而使得策略网络陷入局部最优，因此需要设计启发因子辅助注意力有侧重地分布在不同的交会时刻。

在第t步解码中，计算Tt-1时刻的交会目标It-1到未访问目标j在可行时间区间内的任意时刻k的速度增量，则启发式因子ηj，k的表达式为

式中：Δvmax为所有可行速度增量的最大值。将其与式的兼容性进行加权求和，经过softmax 函数后得到解码器相对于前t-1步的条件概率：

式中：β为启发因子ηj，k相对于兼容性的权重。

2.3 策略网络架构与决策流程

不同于常规的顺序串联多个全连接层的神经网络架构，结合注意力机制的策略网络往往需要拆开这种顺序关系，并对多个仅经过一次线性映射后的向量进行单独处理。此外，不同步长下的掩码约束对策略网络πθ的输出也至关重要。综上，πθ的网络架构与决策流程如图3所示。

图3 基于注意力模型的策略网络架构和决策流程Fig.3 Architecture and deciding process of policy network based on the attention model

图中，最上方为二维掩码矩阵，行向量为时刻，列向量为目标，白色表示当前时刻的目标满足掩码约束，浅灰色则相反，深灰色表示上一步解码的位置；中间则是解码的输入输出，一直循环直至所有目标都被选出；下方为πθ的神经网络架构，总共有6个线性全连接层，每次解码时hc都会更新，使得右侧参数一直变化，而左侧参数保持不变。

3 基于REINFORCE算法的参数更新

随机策略函数的选择概率p（θπ）可利用链式法则拆解成每一步条件概率的累乘：

基于p（θπ）可以确定一组序列和时刻，进而得到回合总奖励R（π），目标函数为R（π）的期望值：

式中：期望值为遍历交会的速度增量之和，期望越小交会序列越好，因此需要利用梯度下降对其进行寻优。

带基线的REINFORCE 算法目前是强化学习解决TSP等路径规划问题的高效算法［14］。该方法通过整个回合的采样值代替收益评价指标，因此参数是基于回合更新的。通过引入一个不依赖于策略网络的基线函数fbl作为实际奖励的期望值，在不影响目标期望值的同时降低其方差，从而增强网络的泛化能力。期望值的梯度为

式中：d为采样样本数。通过链式法则将选择概率的对数lnp（θπ）替换成每一步决策的条件概率的对数之和，然后基于蒙特卡洛采样近似获得目标函数J对参数θ的梯度值。fbl可根据文献［20］提出的贪婪rollout 策略进行拟合，如果当前训练回合下随机采样的策略网络πθ得到的完整序列奖励优于贪婪采样的基线函数网络πθbl，且经过单边配对t 检验得到的值小于置信度α，则用θ更新一次θbl。训练回合数越大，基线函数越接近实际奖励值R。算法共涉及两层循环，具体流程如图4所示。

图4 基于REINFORCE算法的参数更新流程图Fig.4 Flow chart of parameter updating based on REINFORCE algorithm

4 仿真试验

多星交会任务通常以轨道高度和倾角差异较小的碎片云或卫星集群为对象，并且在上层多对多分组优化中轨道异面度比较集中的目标会被分到一组，以提高单个航天器交会目标的数量。因此，单对多序列优化的空间目标分布于半长轴a、倾角i和升交点赤经Ω 分布差异较小的近圆轨道上。此外，由于多星交会问题没有理论最优解，为了验证学习方法在不同目标数量下的精度与泛化能力，通过应用于GTOC9 的改进蚁群算法［7］提供较优解，并将学习结果与之进行对比验证。

4.1 训练配置

4.1.1 数据集

通过限定轨道根数取值范围构造强化学习的数据集，轨道参数的取值范围见表1，符合碎片云或卫星集群的基本特征。在参数训练过程中，数据的随机采样服从均匀分布。

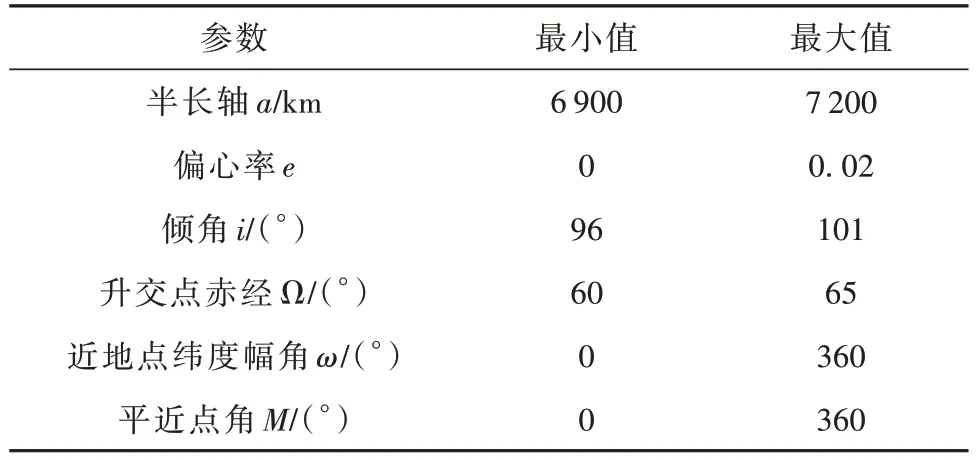
表1 训练数据的轨道根数分布范围Table 1 Range of orbital elements for training

在J2长期项摄动影响下，目标的轨道根数中半长轴a、偏心率e和倾角i不变，升交点赤经Ω 和近地点幅角ω缓慢漂移，而相位M则呈周期性变化。仿照TSP问题提取目标城市的位置坐标作为神经网络的输入，多星交会问题也可将轨道根数转成位置和速度作为输入张量x。

4.1.2 任务场景参数

以单航天器在20 天内交会10 个目标为基本训练场景，两两目标之间的最大转移时间设为8天，包含最少驻留时间ΔTstay=0.5 天。由于没有太阳光照等与星历相关的约束条件，因此对初始历元没有要求。航天器的初始位置设定参考GTOC9，即与第一个交会目标重合，没有额外设计航天器的初始部署轨道。

考虑到交会序列成本随时间的变化呈现出多峰性，若网格数m设太大则注意力过于分散造成学习效果不理想，而m设太小则会使得解的质量偏低。因此m设为80，每个时间网格为0.25天。

4.1.3 超参数

超参数是搭建、训练神经网络的基本参数，可能会影响训练结果但无法进行寻优，最终通过人为经验加上小范围调试给定。这些超参数主要跟网络模型以及训练参数相关，相关数值见表2。

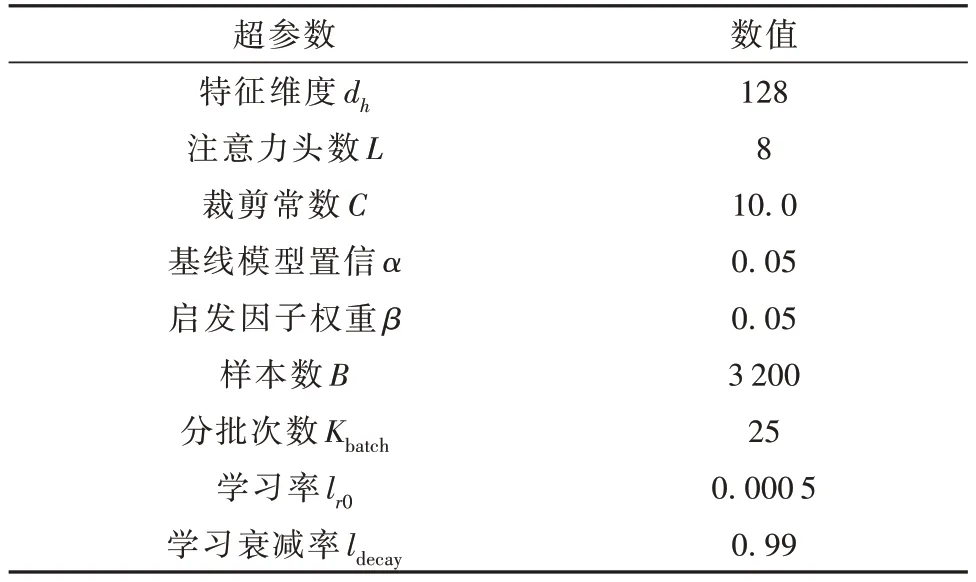
表2 超参数配置Table 2 Configuration of hyperparameters

表中，样本数B是指一次性放入GPU 中进行批量计算的数据量，为了提高训练效果且受显存大小限制需要分批次对样本进行训练；学习衰减率ldecay表示在训练中网络参数θ会随着训练代数g的增加而衰减，学习率的表达式为

4.2 结果分析

4.2.1 训练结果

训练总轮数设为200 代，每代分批训练25 次，因此累计迭代次数为5 000 次。在每回合的批量样本的平均奖励值（实质上是惩罚）指标越小，意味着模型θ的训练效果和泛化能力越好。在10 星交会任务中的这两类指标数值随回合数和迭代次数的增加而变化的情况分别见图5。

图5 10目标交会的训练结果Fig.5 Training results of 10-target rendezvous

从图中可以看到，随着训练次数的增加，样本集的平均速度增量在逐渐下降，并且带基线的目标函数值也在0 处附近振荡，说明策略网络到达了局部最优，整个训练过程也趋于稳定。

在显卡配置为GTX1050Ti 的4G 显存中，10 目标交会场景每训练1 代需要约42 s，200 代累计训练约2.3 h。因为解码流程是串行的，所以目标序列越长，训练时间越长。而其余参数，如时间网格m、特征维度dh等，都不会随着取值的小范围波动而对训练时间造成显著影响。

4.2.2 与ACO对比分析

文献［7］在改进蚁群算法时将信息素矩阵拓展了时间维度，应用于本问题中的时间间隔与网格数m一致，底层采用相同的成本估计算法，其余参数配置为：蚂蚁数为35，进化代数为200，启发式权重参数为2.0，衰减系数为0.9。随机选择50 组算例，RL方法与ACO 算法的序列成本的绝对和相对误差见图6。

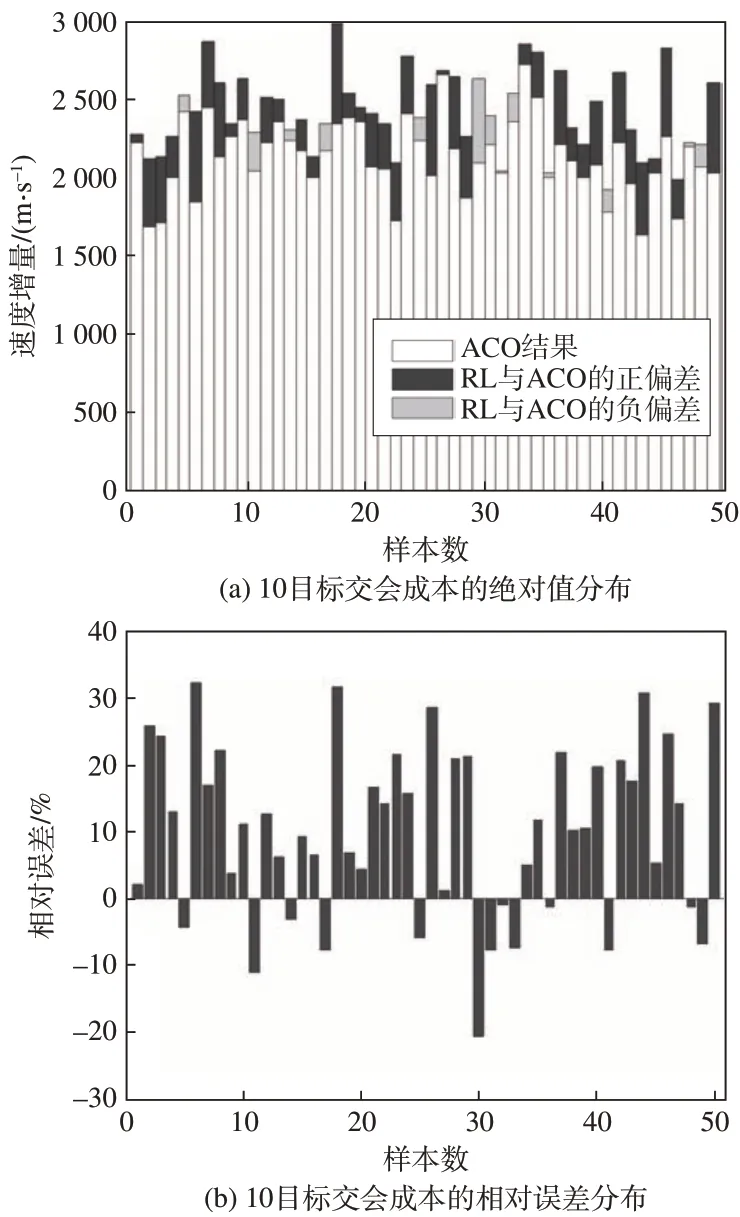
图6 基于RL与ACO的10目标交会成本对比Fig.6 Comparisons of costs of 10-target rendezvous by RL and ACO

图中，ACO 算法得到的50 组样本的序列成本均值为2 170 m∕s，RL 方法估计的序列成本均值为2 379 m∕s。以ACO 算法的优化结果为真值，则RL方法估计成本的平均相对误差为9.7%，平均绝对误差为208.8 m∕s。50 组样本中有13 组的估计值优于ACO算法。

以单个序列为例，RL 方法与ACO 算法分别得到的序列、时间和成本情况见表3。

表3 单个算例的优化结果对比Table 3 Comparison of optimization results of the proposed method and ACO in a single example

表中，序列1 的成本相对误差为3.6%，序列重合度为40%，任务时长为408 h；序列2的成本相对误差为-4.3%，序列重合度为60%，任务时长为456 h。这说明轨道面分布差异较小的序列成本随时间变化的局部极值点较多，存在多组序列和时间不尽相同的解，其转移成本是相近的。

其次对RL 方法与ACO 算法在计算时间上的差异进行比较。在CPU 进程数为28的计算机上，ACO算法对10 目标交会的单个算例的平均优化时间为3.8 min，50 组算例累计约3.2 h。而经过预训练的RL 方法测试这些算例的时间约50 ms，加上2.3 h的预训练时间，总时间仍短于ACO 的优化时间。因此基于强化学习的多星交会序列估计方法在满足一定精度的同时可大大提升计算效率。

4.2.3 不同交会目标对比

为了测试训练网络在不同交会目标下的泛化能力，将训练10目标交会的网络直接对8和12目标的50 组算例进行估计，其余条件不变，同样与ACO算法得到的结果进行对比，2 种情况的序列相对误差分布见图7。

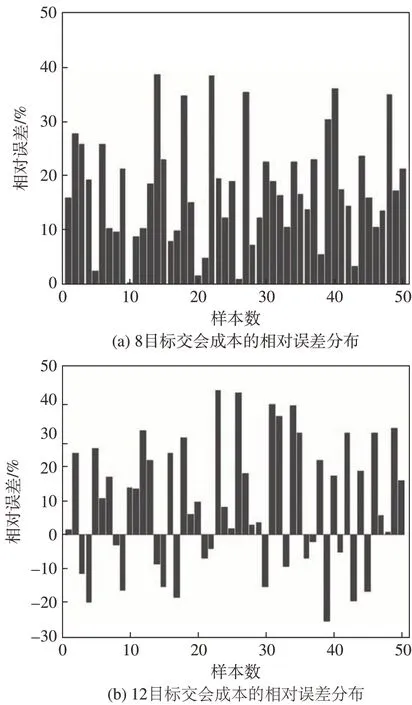
图7 基于RL与ACO的8和12目标交会成本对比Fig.7 Comparisons of costs of 8-target and 12-target rendezvous by RL and ACO

从图中可以看出，由10目标训练得到的网络参数一定程度上也能适用其余目标的交会场景，对8和12目标的估计成本相对误差为15.1%和11.0%。当目标数量越少，ACO 算法的寻优效果更好，RL 方法的泛化误差相对变大，且没有得到比ACO 更好的解；而数量越多，RL方法的适应性优于ACO，估计精度相对稳定，且能够得到比ACO更好的序列解。

4.2.4 不同训练场景对比

此外，交会目标数据集的轨道根数分布程度也会影响训练结果。当进一步扩大目标集的半长轴a、倾角i和升交点赤经Ω 的分布范围，将其上限调整为7 300 km、102°和70°，则RL 方法的估计精度会有所降低，但训练时间不受影响，与ACO 算法的结果对比如图8所示。

图8 基于RL与ACO的10目标交会成本对比Fig.8 Comparisons of costs of 10-target rendezvous by RL and ACO

图中，ACO 算法得到的50 组样本的序列成本均值为2 918 m∕s，RL 方法估计的序列成本均值为3 340 m∕s。以ACO 算法的优化结果为真值，则RL方法估计成本的平均相对误差为12.2%，平均绝对误差为421.5 m∕s。50 组样本中有6 组的估计值优于ACO 算法。当目标分布更分散时，序列成本随时间变化的多峰性增强，导致学习效果降低。

5 结论

针对多星交会序列的端对端优化提出了基于注意力模型的强化学习方法，将时间维度引入注意力模型中，并以速度增量为启发因子，对学习方法的策略网络进行引导，使其能够对不同时刻下的目标进行决策。将所提方法应用于多星交会序列场景中，并与蚁群算法的优化结果进行对比。在对轨道分布较为集中的10目标交会场景中，强化学习方法与蚁群算法对50 组算例的序列成本的平均相对误差为9.7%，且前者的估计时间远小于后者。当交会目标在10附近波动时，神经网络也有较好的估计精度。此外，进一步扩大训练集的轨道根数分布范围，学习方法的估计精度会有所降低。

本文所提方法能够在上层分组打包问题中对单对多访问序列和时间进行快速估计并得到精度尚可的转移成本，从而辅助指派算法更好地搜索全局解。