一种基于目标分层架构的变形飞行器智能规划方法

周愉，王永海，杨 丁，吴志刚，王剑颖

（1.中山大学航空航天学院，深圳 518107；2.空间物理重点实验室，北京 100076）

0 引言

近年来，随着飞行器任务剖面日趋复杂以及智能技术的不断发展，智能变形飞行器逐渐成为航空航天领域的研究热点［1-5］。其中，变形飞行器的轨迹规划与变形决策是实现飞行器智能自主飞行模式的核心问题，即面向复杂飞行任务与飞行环境，要求飞行器能够在线自主调整气动外形和规划飞行轨迹。由于变形对飞行器动力学特性的改变显著，变形飞行器的动力学模型具有强非线性、强时变的特征，变形飞行器的变形决策与轨迹规划本质上是一类复杂状态下的多变量耦合最优控制问题，很多学者针对这一问题开展了相关研究。

针对飞行器轨迹规划问题，国内外学者做了大量研究［6-7］，主要包括间接法［8-11］、直接法［12-14］以及遗传算法等生物智能优化算法［15-16］，但是上述方法本质上依赖于迭代收敛的数值算法，其收敛时间和求解速度面对复杂轨迹的在线规划需求存在一定的局限性。因此，许多学者为了提高轨迹规划问题的计算速度，研究了基于凸优化算法的轨迹规划方法，如宗群等［17］针对可重复使用运载器（Reusable launch vehicle，RLV）的再入轨迹重构问题，提出一种基于变信赖域序列凸规划的RLV 再入轨迹快速求解方法，有效提升了再入轨迹求解的实时性和收敛性。Li等［18］将凸优化和多分辨率技术相结合，提出了一种新的航天器相对运动轨迹规划策略，提高了计算效率。Pei等［19］针对高超声速飞行器在线轨迹规划问题，提出了一种基于改进序列凸优化方法的快速求解方法，可以对任务突变工况进行快速轨迹规划。近年来，随着机器学习理论的快速发展［20-21］，研究人员将智能算法与轨迹规划技术结合，提出一种基于地面学习的在线应用轨迹规划方法。如Shi等［22］针对二维轨迹规划问题，基于间接法生成数据样本并采用机器学习方法训练神经网络模型，提出了支持在线应用的轨迹规划方法。在此基础上，Wang等［23］考虑带禁飞区约束的三维轨迹规划问题，基于伪谱法与机器学习理论，形成满足实时计算效率的轨迹规划神经网络模型。值得说明的是，上述研究仅针对固定外形的飞行器，而尚未考虑变形飞行器的变形决策与轨迹规划的耦合关系。

针对变形飞行器的变形决策问题，一些学者探索了强化学习在变形飞行器外形优化问题上应用的可行性。如，温暖等［24］以一种抽象化的变体飞行器为对象，基于深度学习与确定性策略梯度强化学习方法，确定变形飞行器的变形方式，使其具有较高的自主性和环境适应性。桑晨等［25］针对可同时变展长及后掠角的飞行器，基于深度确定性策略梯度算法（Deep deterministic policy gradient，DDPG）对变形策略进行学习训练，提升了变体飞行器在不同飞行任务和飞行环境下的飞行性能。Xu等［26］采用DDPG算法控制变形飞机模型进行变形决策训练，实现了智能变形飞机方向舵回路的自主控制。不难发现，上述研究仅针对变形飞行器的外形优化层面，即面向某一气动指标进行优化，同样忽略了变形决策与轨迹规划的耦合关系，因而还未能实现根据实时的轨迹状态而自主调整外形的优化目标。

事实上，引入飞行器的变形维度后，变形飞行器成为更高维度的动力学耦合与更强非线性的复杂系统，其变形决策与轨迹规划二者互相影响、密不可分，理论上应在统一的框架内完成这两个问题的求解。一种可行的方式是将变形量作为轨迹控制量之一，参与到轨迹规划问题中，完成对变形量和轨迹控制量统一求解。如朱睿颖等［27］针对高速无动力变构形飞行器航迹优化与飞行策略设计问题，建立可变构型气动代理模型，以一、二锥展长为变形飞行器外形参数，与攻角、倾侧角共同构成飞行器航迹优化变量，完成航迹优化的同时获取飞行器最佳飞行策略。但是这种方式的求解效率还尚未满足在线应用的需求，且在变形维度增大时，存在多解问题而难以收敛。因此，面向多维变形飞行器的在线自主变形与轨迹规划任务需求，本文在前述研究的基础上，研究变形决策与轨迹规划的一体化智能规划问题，提出一种基于目标分层架构的变形飞行器智能行为规划方法，旨在解决多维度变形飞行器轨迹与变形的一体化在线规划问题。

1 智能行为规划模型

1.1 变形飞行器质点运动动力学模型

假设地球为均质圆球，忽略地球自转，飞行过程中侧滑角为零，飞行器在纵平面内运动，则高超声速飞行器无动力滑翔再入的无量纲运动方程为

式中：z为无量纲地心距，u为无量纲速度，τ为无量纲时间，无量纲化参数分别为R0为地球平均半径，g0为地球引力加速度；θ和φ分别为经度和纬度；速度倾角γ为速度矢量和当地水平面的夹角，在水平面上方为正。速度方位角ψ为速度矢量在当地水平面投影与正北方向的夹角，以正北方向顺时针旋转为正分别为无量纲升力和阻力，且有：

式中：m和Sref分别为飞行器的质量和气动参考面积；ρ为大气密度；Vc为速度V的无量纲化参数；CL和CD分别为升力系数和阻力系数。

1.2 变形飞行器轨迹规划与变形决策协调建模

考虑某变形飞行器有i个变形维度[ξ1，ξ2，…，ξi]，且可以在以下范围内连续变形：

则该飞行器的控制量组合为

随着飞行器可变形部位的增多，其控制量序列的维度也随之升高，直接利用变形量进行轨迹规划的复杂度也呈指数级增长，需要设计一组伪控制量将轨迹规划控制量序列进行降维。

在高超声速飞行条件下，飞行器气动力系数近似满足抛物线阻力极线关系［28］：

在较大马赫数条件下，可近似认为式（5）中的零升阻力系数CD0和诱导阻力因子K为常数。根据上述定义，可以得到升阻比E的表达式：

对于固定外形飞行器，在高超声速条件下，其最大升阻比E*的取值是唯一确定的［29］。而当飞行器具有可变形的特征时，变形飞行器在各个变形组合下都可视作不同的固定外形飞行器，最大升阻比E*也会随着变形状态组合的不同在一定范围内取值。因此，作为一种表征变形状态的关键参数，最大升阻比E*是需要规划的参数之一。此外，在确定了最大升阻比E*后，再通过规划参数泛化升力系数λ，结合式（10）～（12），即可确定升力系数CL和阻力系数CD，从而唯一确定当前时刻的轨迹状态。综上，对于变形飞行器的变形与轨迹规划问题，可将最大升阻比E*和泛化升力系数λ作为伪控制量，即可以将式（4）转化为

以某具有三个变形维度的变形飞行器为例。输出飞行器的气动参数变化范围如图1（a）所示，输出其伪控制量辨识范围计算得到的等效气动参数变化范围如图1（b）所示。从对比图中可以看出，基于伪控制量的等效气动参数包络范围与飞行器真实气动参数包络范围大致重合。统计两者的绝对误差值大小：在升力系数绝对误差中，68.3%的样本小于6.2 × 10-3，95.5%的样本小于1.2 × 10-2，绝对误差最大值为0.018。在阻力系数绝对误差中，68.3%的样本小于4.3 × 10-3，95.5%的样本小于6.2 × 10-3，绝对误差最大值为0.007。

图1 实际气动参数和拟合气动参数对比Fig.1 Comparison of actual and fitting aerodynamic parameters

综上所述，本节所提出的伪控制量组合能够较好地拟合变形飞行器的气动参数模型，利用该伪控制量进行轨迹规划可以对控制序列进行降维，不必直接对攻角以及变形量进行规划。从而，可以将轨迹与变形一体化规划问题解耦为规划伪控制量的顶层轨迹规划子问题和规划真实控制和变形量的底层变形决策子问题。

1.3 轨迹与变形一体化规划的目标分层架构

建立变形飞行器轨迹规划与变形决策协调模型后，设计基于目标分层架构的智能规划方法流程图如图2所示，方法主要包括顶层网络训练、底层网络训练以及训练完成后的在线应用三部分。

图2 基于目标分层架构的智能规划方法流程图Fig.2 Flow chart of intelligent planning method based on hierarchical architecture of objective

变形飞行器顶层轨迹规划网络的训练过程为：首先利用Chebyshev 伪谱法对随机飞行任务进行最优弹道规划，产生大量最优弹道样本，然后通过深度学习方法对产生的地面数据样本进行大规模的学习和训练，形成基于任务需求和当前飞行状态确定轨迹伪控制量的神经网络模型，实时输出任务轨迹需求的气动参数，为变形飞行器底层行为决策提供规划目标。

变形飞行器底层变形决策网络的训练过程为：面向顶层轨迹规划网络产生的气动参数需求，通过深度强化学习方法对大量气动数据样本进行学习和训练，形成基于顶层需求气动参数确定当前变形量与飞行控制量的神经网络模型，使得变形飞行器能够基于学习训练结果，实时输出变形量与攻角组合，实现弹上自主智能变形行为规划。

完成顶层和底层两层网络的训练后，通过两层网络的相互嵌套应用，可以实现在线的轨迹与变形一体化规划。在线应用的过程为：将飞行器每个时刻的飞行状态量与当前飞行任务参数组合后输入顶层轨迹规划网络得到此时刻飞行器所需的目标气动参数，将目标气动参数输入底层变形决策网络后得到能够实现目标气动参数的变形量与攻角的优化组合，最后基于该变形量与攻角的组合决策指令，通过弹上变形控制与姿态控制实现期望的变形量与攻角，从而实现面向任务需求的期望目标轨迹。值得说明的是，由于顶层轨迹规划与底层变形决策都是由训练好的神经网络直接产生指令，而不需要在线迭代优化的过程，因而能够实现较高的计算效率，满足实时在线应用需求。

2 基于深度学习的顶层智能轨迹规划方法

2.1 最优轨迹样本生成

考虑到变形飞行器在再入初始时刻和终端目标点的飞行状态均在一定范围内具有不确定性，为了使样本能够尽量覆盖实际飞行过程中的飞行状态，本文在生成最优轨迹样本时，设定飞行初始和终端状态的范围为

式中：t0为飞行起始时间，tf为飞行终端时间。然后基于Chebyshev 伪谱法在上述范围内进行最优轨迹优化，为保证再入飞行器在结构和热防护上具有可靠性，需保证飞行过程严格满足热流密度、动压和过载约束。因此，设置Chebyshev 伪谱法的过程约束条件如下：

为了使飞行器飞行效率最高，将优化目标设定为飞行时间最短，即：

基于上述条件，采用Chebyshev 伪谱法进行优化轨迹求解。在Chebyshev-Gauss-Lobatto 点（CGL点）上将连续时间状态变量和控制变量做离散化处理，并将离散点作为节点，通过构造Lagrange 插值多项式来逼近实际飞行的状态变量和控制变量；然后，对多项式求导来逼近状态变量对时间的导数，将微分方程约束转换为代数约束；最后，通过数值积分计算性能指标中的积分项。通过上述方法，将最优控制问题转化为非线性规划问题［30］。

设最优控制问题的时间区间为[t0，tf]，采用Chebyshev 伪谱法则需将时间区间转换到[-1，1]，因此对时间变量t作变换：

Chebyshev伪谱法的插值点（CGL点）选取为

以N次Lagrange 插值多项式作为基函数描述控制变量以及状态变量：

状态变量的一阶微分可以通过对式（20）求导来近似得到，同时将动力学微分方程约束转化为代数约束。

所以动力学方程满足：

综上，可基于飞行环境和任务目标建立轨迹规划问题的约束方程和优化目标函数等，完成地面大规模数据样本生成。

根据飞行任务设定对轨迹规划的各项约束进行设置。其中，弹道初始和终端条件见表1，变形飞行器的热流、动压和过载约束见表2，伪控制量约束见表3。

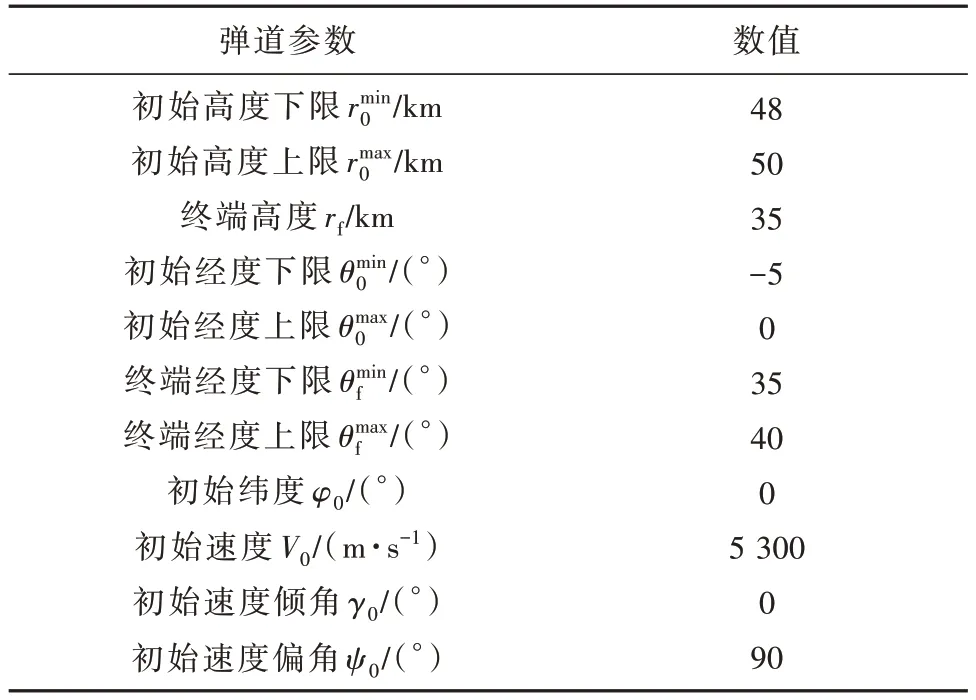
表1 弹道初始终端条件Table 1 Initial and termination conditions

表2 弹道过程约束Table 2 Process constraints of trajectory planning

表3 伪控制量过程约束Table 3 Process constraints of the pseudo-control quantity

综合上述条件设置，利用Chebyshev 伪谱法输出4 000 条最优弹道作为训练样本。将Chebyshev伪谱法输出的4 000 条优化弹道的状态量和控制量按照1 s的时间间隔离散后，将每个时刻的飞行状态量、此条弹道的初始和终端状态以及当前时刻的轨迹控制量记录并存储，将所有优化弹道每一时刻的弹道数据作为顶层轨迹规划的数据样本，支撑神经网络模型的训练。

2.2 顶层轨迹规划网络建模与训练

变形飞行器顶层轨迹规划本质上是基于飞行器当前状态、初始状态和终端状态，输出当前时刻的最优轨迹控制量，为了描述这种复杂非线性的映射关系，本文基于按误差逆传播算法（Back propagation，BP）训练的多层前馈神经网络建立变形飞行器顶层轨迹规划模型。假设神经网络有L个输入节点，M个输出节点，R个隐含节点，有N个数据样本用于网络训练，则对于输入输出序列分别为xp和tp的样本p，隐含层第i个神经元的输入可以表示为

式中：f为隐含层激活函数。同理，该神经网络输出层第k个神经元的输入和输出可表示为

式中：ωki为隐含层第i个神经元与输出层第k个神经元之间的权值，bk为输出层第k个神经元的阈值。

对于N个训练样本，总均方值误差可以表示为

式中：Δωki为输出层与隐含层连接权值的修正量，Δωij为隐含层和输入层连接权值的修正量，Δbk和Δbi分别为输出层和隐含层神经元阈值的修正量，η为学习率。

对于本文所提出的顶层轨迹规划网络模型，输入层包含10个节点，分别表征飞行器的飞行任务和当前状态。输出层包含2 个节点，分别表征飞行器在当前时刻所需的最优气动参数。则训练样本p的输入序列xp可以表示为

值得说明的是，考虑到神经网络数值计算量值的影响，需要对各个物理量进行归一化处理，即神经网络模型输入量和输出量分别为归一化后的物理量，本文采用如下的归一化方法：

以2.1节中4 000条优化弹道产生的4 138 312组数据作为数据样本，根据BP神经网络模型对应的输入输出序列，随机选取4 133 312组数据作为训练集，5 000 组数据作为测试集。利用Pytorch 平台搭建BP神经网络进行训练，神经网络参数设置如表4所示。

表4 神经网络参数Table 4 Neural network parameters

其中，Batch-size 代表一个训练批次所包含的样本数，Epoch 为训练的总轮数。训练过程中，神经网络的均方误差值下降过程如图3 所示，最终稳定在10-5水平。训练完成后，为了定量地体现神经网络的逼近精度，统计两者的绝对误差值大小：在升力系数绝对误差中，68.3%的样本小于1.92 × 10-5，95.5%的样本小于1.0 × 10-3，绝对误差最大值为0.063。在阻力系数绝对误差中，68.3%的样本小于5.12 × 10-5，95.5%的样本小于2.45 × 10-4，绝对误差最大值为0.015。

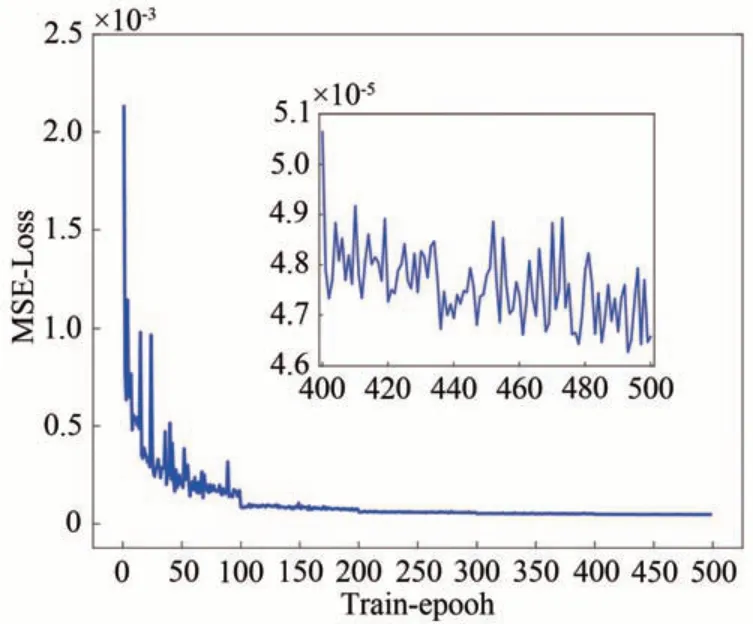
图3 神经网络训练过程Fig.3 Training histories of neural network

3 基于强化学习的底层自主变形决策方法

3.1 强化学习模型建立

马尔科夫决策链是强化学习中经典的形式表达，其基本形式可以表示为{S，O，A，P，R}。其中，S为状态集，O为状态集中可观测部分，A为动作集，P为状态转移概率，R为回报函数。在本文研究对象中，状态集S被定义为飞行器所处的高度h、飞行马赫数Ma以及飞行器顶层轨迹规划网络所规划的升力系数和阻力系数，且4 个状态量均可被观测，即：

动作集A为飞行器的攻角α以及3个变形维度。考虑到各变形维度的变形尺度不一，于是用变形系数μ1，μ2，μ3来表征飞行器的变形量，即：

则动作集A可表示为

对于本文研究的变形飞行器，当飞行状态Ma，h和气动外形已知时，其气动参数CL和CD由飞行器的气动模型唯一确定，则该马尔科夫决策链中的状态转移概率P也是已知确定的。

设计非稀疏奖励函数：

考虑到变体飞行器的机体形变是一个连续过程，本文采用具有规划连续动作能力的深度确定性策略梯度强化学习算法DDPG 对变形飞行器智能体进行训练，使其能够在顶层轨迹规划网络做出气动参数规划后，自主决策出能够适应气动参数需求的最佳攻角和变形状态，从而使飞行器能够根据飞行任务，保持最佳气动外形状态。基于DDPG 算法的变形飞行器底层自主变形决策网络训练流程图如图4所示。

图4 DDPG算法流程图Fig.4 Flow chart of DDPG algorithm

3.2 底层智能变形决策网络训练

设置DDPG算法训练参数如表5所示。

表5 DDPG训练参数设置Table 5 Hyperparameter setting

由于本文提出的底层强化学习任务为对顶层网络做出的气动参数规划快速响应，给出相应的变形量和控制量，于是设置每回合最大时间步数为1，即要求飞行器经过一次变形决策便实现对气动数据的跟踪。由于每回合训练不存在步数累积奖励，重设任务的难度不同，每回合智能体获得的奖励值也会随之波动，于是可以通过输出训练前平均奖励值来观察智能体学习情况。经过仿真训练，智能体获得奖励函数值曲线如图5所示，从奖励函数曲线可以看出，在前1 000 个回合内，智能体还处于随机探索阶段，未开始学习，1 000 个回合后智能体开始学习，平均奖励值开始增大，在10 000 个回合左右，平均奖励函数值达到最大，最终稳定于0.98左右。

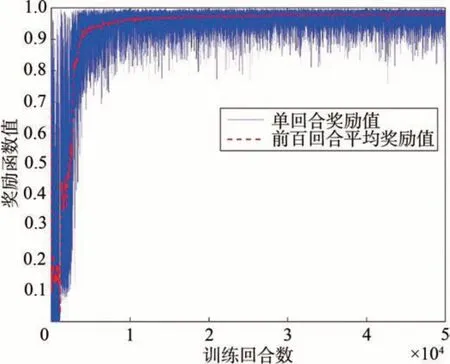
图5 奖励函数曲线Fig.5 Reward function curve

保存完成训练的智能体后，随机从顶层网络规划数据样本中采样1 000组初始状态利用保存的智能体进行气动参数跟踪。统计真实气动参数和期望气动参数之间的绝对误差值大小：在升力系数绝对误差中，68.3%的样本小于0.29 ×10-2，95.5%的样本小于0.47 × 10-2，绝对误差最大值为0.005。在阻力系数绝对误差中，68.3%的样本小于0.41 × 10-2，95.5%的样本小于0.8 × 10-2，绝对误差最大值为0.011。

4 数值仿真与结果分析

为了验证本文提出的轨迹与变形一体化规划方法的有效性，在2.1 节给出的任务设定范围的边界和内部给出三组飞行任务，基于本文所提出的目标分层变形与轨迹一体化规划方法进行仿真，当飞行器与目标位置的距离最小时判定为到达弹道终点并停止迭代，三组工况的具体条件设置以及仿真结果如表6 所示，轨迹曲线如图6 所示。与目标位置相比，三组工况的终端高度误差最大值为302 m，平均值为168 m，终端经度误差最大值为-0.038°，平均值为0.017°。从仿真结果可以看出，本文所提方法能够满足变形飞行器轨迹规划的精度要求。

表6 飞行任务参数与仿真结果Table 6 Flight mission parameters and simulation results

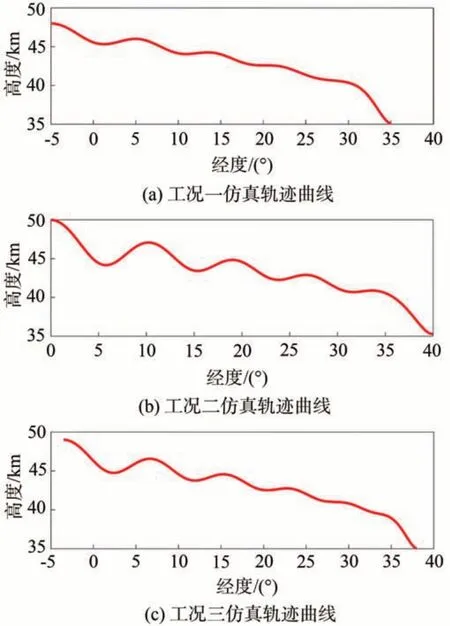
图6 各工况仿真轨迹图Fig.6 Trajectory of each working condition

除了规划精度之外，轨迹规划方法所消耗时间的长短也是影响其能否在线应用的重要因素。在（Intel（R）Core（TM）i7-10700K CPU @ 3.80GHz）处理器平台下，对于本节设置的三组工况，轨迹总航时以及利用本文所提方法进行规划所消耗的规划解算用时已经在表6中列出。作为对比，在相同条件下，利用Chebyshev 伪谱法（32 个配点）进行规划所消耗的时间分别为15.837 s、15.962 s 和16.081 s，本文所提方法解算消耗时间在其基础上分别缩短了94.2%、94.4%和94.3%。综上所述，在飞行器地面最优轨迹规划上，本文所提方法相比传统的伪谱法具有解算时间上的优势，且解算精度满足规划要求。在飞行器在线轨迹规划上，本文所提方法能够仅根据实时飞行状态和飞行任务直接生成规划与决策指令，具备在线应用的潜力。

为了进一步说明本文分层智能规划方法的有效性，作为对照仿真，基于本文分层智能规划方法生成的轨迹称为实际规划轨迹，将利用直接法所规划得到的轨迹称为参考标准轨迹。以工况三为例，其轨迹状态量曲线、飞行过程中的气动参数曲线以及控制量曲线分别如图7、图8 和图9 所示。从图7中可以观察到，在飞行全过程中，本文所提方法规划的各个轨迹状态量与标准序列都基本重合，四个状态量终端误差分别为75m，0.006°，11.94 m∕s 和0.0 074°。图8 的结果显示，在整条序列中，本文所提方法的顶层网络输出的目标升阻力系数指令与标准升阻力系数之间的绝对误差最大值分别为0.004 和0.001，误差百分比分别为0.96% 和1.03%。而底层网络输出的控制量指令对应的升阻力系数与目标升阻力系数之间的误差最大值分别为0.003 和0.007，误差百分比分别为1.02%和6.08%。从仿真结果来看，此误差没有使飞行状态相对于标准轨迹产生大幅度的偏差，满足精度要求。三条曲线的基本重合说明顶层网络学习到了由飞行任务和飞行状态到目标气动参数之间的映射关系，能够得到与成熟方法一致的可靠结果；底层网络学习到了由目标气动参数到最优控制量之间的映射关系，即所输出决策量能够实现顶层期望的目标气动参数。从图9 可以看出，飞行器在飞行过程中进行了连续的攻角和变形量规划，且攻角和变形量指令变化均匀，利于后续控制器的设计。综上所述，本文所提出的轨迹与变形一体化规划方法能够根据飞行任务和飞行状态输出满足精度要求的最优控制指令，使变形飞行器以较高精度到达任务目标位置。

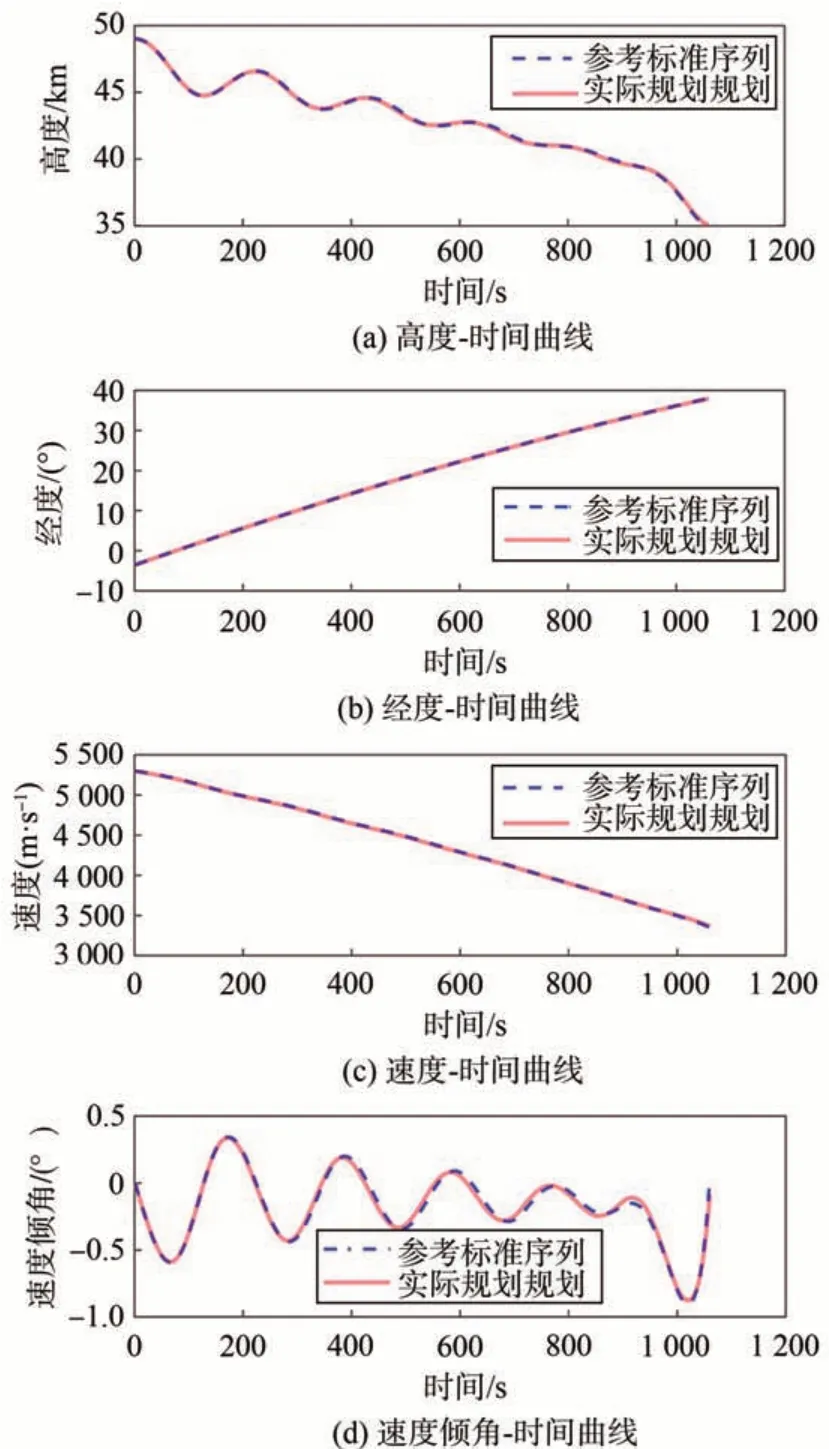
图7 仿真状态量对比Fig.7 Comparison of state quantity

图8 分层网络规划气动参数对比Fig.8 Comparison of output aerodynamic parameters

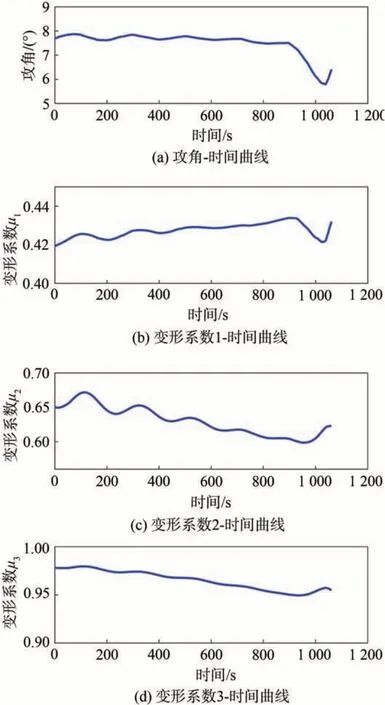
图9 控制量曲线Fig.9 Control quantity curve

为了验证本文提出的轨迹与变形一体化规划方法的泛化性能，在表1 所设置的任务范围内随机生成1 000 组飞行任务，利用本文提出的规划方法进行轨迹与变形一体化规划。统计1 000 条生成轨迹的终端高度、经度与任务目标高度、经度之间的误差，仿真结果与任务目标之间的绝对误差统计结果如表7 所示。在高度绝对误差中，68.3%的样本小于149.5 m，95.5%的样本小于253.8 m，最大值为303.4 m。在经度绝对误差中，68.3%的样本小于0.02°，95.5%的样本小于0.06°，最大值为0.117°。从仿真结果可以看出，对于在训练范围内的飞行任务，本文提出的规划方法具有较好的泛化性能，能够根据不同飞行任务快速规划出符合精度要求的轨迹和变形量序列。

表7 终端误差统计分析Table 7 Statistics for terminal guidance error analysis

5 结论

针对高超声速变形飞行器实时随机飞行任务轨迹规划问题，本文提出一种基于深度神经网络和强化学习的分层嵌套规划方法。利用深度神经网络的泛化性能和适用于连续动作的强化学习的自主决策能力实现变形飞行器的轨迹与变形一体化规划。主要结论包括：

1）推导了轨迹控制量与变形量的一体化协调模型，建立了包含顶层轨迹规划与底层自主决策两个层面的智能行为规划目标分层架构；

2）针对顶层轨迹规划问题，建立了顶层规划深度BP神经网络模型，并基于伪谱法和数据离散方法生成大规模最优轨迹数据样本，实现了基于反向误差传播方法的模型训练与优化，获取能够预测轨迹伪控制量的深度神经网络模型；

3）针对底层控制量决策问题，建立了变形飞行器变形量与气动角度的深度强化学习环境模型，基于深度强化学习DDPG 算法对变形飞行器进行训练，形成由最优气动参数指令到轨迹控制量与多维变形量的深度网络模型，实现面向顶层网络输出的变形量与气动角度的快速响应；

4）结合顶层轨迹规划与底层自主决策神经网络，对变形飞行器再入段随机飞行任务进行了蒙特卡洛打靶数值仿真验证。结果表明，本文提出的变形飞行器轨迹与变形一体化分层快速规划方法能够根据飞行任务快速规划出最优轨迹和变形控制量序列，规划精度较高，且与传统轨迹规划方法相比，所提出的方法能够明显缩短计算时间，具备在线应用的潜力。