参数自适应凸优化下的月面着陆最优轨迹规划

穆荣军，邓雁鹏，吴 鹏

（哈尔滨工业大学航天学院，哈尔滨 150001）

0 引言

为顺利实施月球着陆探测器自主避障、保证精确安全着陆，通常将月球着陆过程分为3个阶段，即动力下降段、接近段与着陆段，如图1所示［1］。这些阶段通常还可能根据任务不同进一步细分，例如中国的嫦娥系列探测器［1-4］。以嫦娥三号为例，月球着陆器在动力下降段前处于远地点100 km、近月点15 km的转移轨道上。自近月点附近开始进入动力下降段。动力下降段的主要目标为尽可能降低着陆器的高度和速度。在动力下降段，着陆器高度从15 km降低到2.4 km，速度将从1.7 km∕s 降低到0 左右［5］。该阶段通常会消耗掉约80%的燃料，因此该段制导算法要求在着陆器具有初始状态误差和模型不确定性的情况下尽量降低燃料消耗，同时具有足够的位置和速度精度以达到后续接近段的入口状态要求。

图1 典型月面着陆过程Fig.1 Typical lunar landing process

嫦娥系列探测器为在动力下降阶段尽可能地节省燃料，采用了具有燃料次优特性的线性正切制导律。但线性正切制导律不能控制着陆器的航程，因此并不能用于需要精确定点着陆的应用场景。例如，嫦娥三号的预定着陆区是位于月球虹湾的一个长356 km、宽91 km 的带状区域［6］。这显然不能满足未来月球探测的任务需求。

中国计划在未来10年内开展载人登月活动，同时建立有人驻守的月球基地［7］，这就需要着陆器能够在基地附近定点精确着陆；此外，随着对月球探索的进一步深入，月球着陆器还需要能够在具有复杂地形的高科学价值目标附近精确着陆［8-9］。以上均需要下一代月球探测器具有精确定点着陆的能力。而动力下降段作为月面着陆过程中飞行时间最长，燃料消耗最多，航程最远的主要阶段，其轨迹规划的质量与制导的精度将直接决定最终着陆精度与燃料消耗，因此许多机构和个人对此进行了深入的研究［10-11］。

现有的月面着陆制导算法分为闭环显式制导算法和标称轨迹跟踪制导算法两类［12］，其中显式制导律以A2PDG［13］、基于分数多项式的动力下降制导［14］以及ZEM∕ZEV 制导律［15-17］为代表，在具有良好的自主性和实时性的同时也具有一定的抗干扰能力，能够保证末端制导精度。

相较于闭环显式制导算法而言，基于轨迹优化算法的标称轨迹制导方法首先需要利用最优化原理，按照一定的目标及约束条件设计标称着陆轨迹。该方法通常消耗燃料更少，具有更强的鲁棒性。其中，凸优化算法由于其具有多项式级的计算复杂度与理论上的全局最优性，而得到了广泛的研究与应用［18-21］。

然而，常见的飞行器轨迹规划动力学模型约束和控制量约束都是非凸的，因此需要先将该问题通过凸化转变为凸问题再进行求解。常见的凸化方法主要有序列凸化和无损凸化两种［22］。其中无损凸化技术通过引入松弛变量的方法将非凸约束松弛为凸的形式，再证明松弛问题的最优解也是原始问题的最优解，实现原始非凸问题向凸问题的等价转换。该方法相较于序列凸化，具有无需原始参考轨迹，同时不需要添加附加的信赖域约束，收敛特性良好的特点。Acikmese 等［21］针对火星着陆问题提出了一种用于动力下降制导问题的凸规划算法，该算法将火星着陆问题通过无损凸化最终转化为一个二阶锥规划（Second order cone programming，SOCP）问题，进而保证了燃料最优。随后这一方法得到广泛的关注，并在不同方面得到进一步地改进。有的学者为提高该方法的收敛性，收敛速度，精度等，针对该方法本身做了改进。

文献［23］进一步明确了凸优化所需要的最佳飞行时间（time of flight，TOF）的确定方法；文献［24］将凸优化与伪谱法结合，通过合理的选择节点集合，减少了节点个数，节约了CPU 时间，提高了运算精度。文献［25］进一步提出将该方法运用到了交会对接方面。

另一方面，很多学者针对该方法对于复杂障碍环境，复杂动力学环境的适应能力做出了相应改进。例如文献［4］对月面着陆器动力下降制导过程中时变的惯性加速度和重力加速度难以估计与补偿等问题提出一种基于序列凸优化的在线制导算法，将时变加速度剖面同伦地添加到原非线性模型中序列迭代求解，使得该算法不依赖初始参考轨迹，增强了算法的自主性和多种应用场景适应能力。文献［23］通过同伦方法与不动点迭代思想处理时变的气动约束，在此基础上设计了基于凸优化的火箭垂直在线轨迹规划方法。文献［26］将凸优化与曲率调整策略结合在了一起，在保证避障能力的同时降低了油耗。文献［27］考虑了在具有不确定性情况下的最优轨迹规划。文献［28］通过对该算法进行改进，将其应用于具有不规则形状与不规则引力场的小行星着陆。

在另一方面，不确定性广泛存在于航天系统设计中，对系统响应、最终控制精度等影响很大，在系统不确定性超过设计冗余时可能导致设计失败。因此，有必要针对系统不确定性建模，以提升系统精度及鲁棒性。

为解决上述问题，许多学者提出了先进控制理论［29］，如自适应神经网络控制［29-32］、非参数自适应控制［33］和滑模控制［34-35］等方法。此外，部分学者针对系统不确定性进行在线辨识，同时通过在线辨识结果对模型进行在线补偿以降低系统的不确定性。文献［36］针对小推力航天器轨道保持问题，设计了一种基于改进型条件积分滑模面和径向基函数神经网络估计器，并通过实时补偿实现高精度轨道保持。文献［37］针对空间探测问题，对不确定扰动按从轻到重4 个等级进行划分，通过模糊神经网络进行评估并采取响应策略，从而提高任务的可靠性及灵活性。文献［38］利用范数自适应控制算法和自适应估计算法有效估计充液航天器扰动的未知上界以及液体晃动的位移变量，实现了对充液航天器的自适应鲁棒控制。在月球探测方面，文献［39］针对月球着陆过程中需要高精度悬停的需求，设计了以位置为量测量的观测器，以实现对质量和推力不确定性的快速估计和补偿。文献［40］将月球上升段制导参数的在线估计问题转换为离散线性系统的最优估计问题，解决了动力显示制导的参数自适应问题。

本文以嫦娥五号探测器所携带的着陆器与上升器组合体为例，提出了一种利用现有的发动机实现精确月球着陆算法。在标称状态下，通过合适的转移轨道和推力剖面规划即可以实现精确着陆。然而，考虑到在下降着陆过程中，由于发动机工作条件、加工工艺、氧化剂和燃料的状态存在一定的不确定性，因此，着陆器的比冲存在一定的不确定性；同时，由于工质挥发等因素，着陆器的质量也具有一定的不确定性［26，39］，这些不确定性会影响最优轨迹规划效果，使得所规划轨迹丧失最优性，增加燃料消耗。为消除系统的不确定性，尽可能地节约燃料，提升着陆精度，本文提出了一种基于参数自适应凸优化的轨迹规划算法。该算法以凸优化轨迹规划为基础，考虑到飞行过程中比冲和实时质量的不确定性，为实现参数的快速高精度收敛，通过设计最优观测器，利用加速计量测数据对以上参数进行在线实时估计。在估计结果达到收敛后再利用凸优化重新进行轨迹规划，以得到符合实际参数的最优轨迹。

本文编排如下：在第1 节首先介绍了月面着陆动力学模型，引入了基于凸优化的最优轨迹规划方法；在第2节本文首先考虑了不确定性模型，并基于该模型设计了最优状态观测器，利用该观测器实现对着陆器参数的在线实时估计；最后通过仿真分析验证了该观测器的收敛速度及最终收敛精度，并通过蒙特卡洛打靶试验证明了该方法仅仅需要发动机具有离散的推力域，同时能够提升制导精度。

1 基于凸优化算法的着陆动力学模型

1.1 总体技术方案

为实现月面精确着陆，着陆器所携带的发动机需要具有一定的推力调节能力。目前嫦娥五号所携带的发动机为一台变推力发动机，其采用系统自锁阀与发动机气动阀控制。该发动机可以输出7 500 N的额定推力，也可以输出1 500 N 至5 000 N 范围内的任意推力，但该发动机的推力在5 000 N和7 500 N之间无法连续调节［41-43］，即该着陆器的推力域约束可以描述为

式中：Fc为主发动机输出推力，F1=5 000 N，F2=7 500 N，F3=1 500 N。

在此基础上，本文进一步探讨一种携带仅具有离散推力域发动机的探测器在月球表面着陆的问题。这种发动机的推力没有任何连续调节能力，仅能按照F1或F2进行输出，即：

而在F1与F2之间，推力并不连续可调。

根据最优化理论，采用凸优化算法进行轨迹规划能够保证在尽量节省燃料的前提下从给定的初始状态转移到预定的终端状态，同时燃料消耗具有最优性，能够满足动力下降段节约燃料的要求。同时，由最优化理论所产生的推力指令遵循最大-最小-最大模式［21］，即先输出最大推力，然后在某时刻切换至小推力输出，最后再切换至最大推力输出，如下式所示：

式中：t1，t2为两个推力突变时刻；tf为动力下降段飞行时间。

根据式（3），最优推力曲线呈现分段恒定的形式，可以断定，式（2）所形成的推力大小在一定区间内不可用的约束本质上并不影响最优解。因此本文采用凸优化算法进行最优轨迹规划，将式（2）的离散推力限制首先松弛为连续的推力区间：

在此基础上，结合着陆器初末状态约束、动力学约束等进一步将该问题进行凸化和离散化，最后转化为SOCP 问题后进行求解。在解出最优推力剖面后，通过主发动机在最大与最小推力之间的切换，实现对该最优推力剖面的跟踪，进而实现月面高精度定点着陆。

此外，考虑到在实际飞行过程中，着陆器的比冲、质量可能与标称值不一致，从而对所规划的轨迹的最优性造成影响，使得燃料消耗增加，着陆精度降低。为解决上述问题，本文根据主减速段标称轨迹来源进一步将主减速段划分为使用标称参数凸优化以及在线参数自适应凸优化的两段，如图2所示。着陆器首先将根据标称参数离线产生一条标称轨迹，并在主发动机点火后沿着该利用标称参数进行最优轨迹规划形成的轨迹飞行；与此同时，在飞行过程中，着陆器将根据发动机推力指令，加速度计的测量结果，利用最优观测器实时估计着陆器质量，比冲等相关参数，在参数达到收敛后再重新进行凸优化，生成新的最优轨迹，并沿着该轨迹飞行。此时由于最优轨迹是根据实际参数生成的，因此能够达到更高的着陆精度，同时消耗更少的燃料。

本文考虑到在月心惯性坐标系下建模不需要考虑惯性力项，因此具有模型简单的优势，故在月心惯性坐标系下建立着陆动力学模型。其中月心惯性如图3 所示，坐标系的原点O位于月心，OzI与月球平赤道面垂直，指向月球北极；OxI在月球平赤道平面上指向J2000 时刻的春分点方向；OyI与另外两轴构成右手直角坐标系。

图3 月球惯性坐标系Fig.3 Lunar inertial coordinate system

图4 月球固联坐标系Fig.4 Lunar fixed coordinate system

此外，考虑到月面固连坐标系较为直观，物理意义明确，本文将在该坐标系下设置仿真初始条件及展示仿真结果。该坐标系的原点OL为着陆器的目标着陆位置，OLxL轴的指向平行于着陆器标称初始位置到目标着陆点的矢量在月面的投影，OLzL竖直向上，OLyL轴与以上两轴组成右手坐标系。

从月球固联坐标系到月球惯性坐标系下的转换关系为：

式中：β为月球固联坐标系与当地正东方向的夹角，以东偏北为正。

1.2 着陆器动力学模型

在月球惯性坐标系下，着陆器的动力学模型为

式中：r(t)，v(t)分别为着陆器t时刻的位置和速度；Fc(t)为着陆器推力；m(t)为着陆器质量；Isp为推力器比冲；ge为标称地球重力加速度；g(t)为月球重力加速度；α=1∕(Ispge)为质量流量系数。

该问题经由凸化和离散化最终可以化为以下SOCP问题［4，19-21］：

通过解式（9）这一SOCP 问题，即可得到最优控制量以及相应的最优轨迹。可以看到式（9）中含有质量流量系数α，根据定义，取决于着陆器比冲；同时其状态量和约束均与初始质量mwet有关，因此有必要对这些量进行估计，降低系统的不确定性，提升优化效果。

2 参数自适应算法

在凸优化过程中需要用到着陆器的比冲、初始质量等参数。如果凸优化使用的参数与实际不一致将影响轨迹的最优性，从而进一步影响燃料消耗与着陆精度。因此，本文设计了一个基于参数自适应的凸优化算法。通过构造最优观测器在线实时估计比冲，质量等参数。并在这些参数达到收敛后重新进行凸优化以保证轨迹的最优性。

2.1 不确定性模型

考虑在着陆过程中，由于发动机工作条件，加工工艺以及氧化剂及燃料状态等存在一定的不确定性，因此着陆器的比冲存在一定的不确定性。同时由于着陆器携带的燃料挥发，物资重量变化等等影响，初始质量也具有一定的不确定性，这样飞行过程中的实时质量亦具有不确定性。因此，本文考虑利用加速度计的在线测量值对比冲及质量进行估计。

假设比冲在飞行过程中保持不变，则质量流量系数也为一恒定值。则着陆器质量和质量流量系数满足以下微分方程：

以加速度计的测量结果作为量测值，则量测方程为

令θ=[mα]=[θ1θ2]，则式（12），（13）可记为

2.2 最优观测器设计

下面针对系统设计最优观测器。考虑观测器模型为：

则H(t)可表示为

式中：P(t)为如下Riccati方程的解

其中，P0，Q，R为正定对称矩阵。

将P，Q，R记为

可将式（16）与式（19）联立展开为

当观测器运行时间t大于T0，且协方差矩阵P满足ρ(P)≤ε时，认为已经收敛到θ。其中，ρ(P)表示矩阵P的谱半径，ε为收敛后P的谱半径上限。在实现收敛后，即可按照如式（9）所示的模型重新进行凸优化，获得新的参考轨迹。

综上所述，参数自适应凸优化算法流程如图5所示。着陆器首先依据离线凸优所产生的标称轨迹进行标称轨迹制导，同时通过制导系统输出的实时推力指令以及加速度计测量数据对实时质量和比冲进行在线参数估计。通过协方差矩阵P的谱半径ρ(P)判断所估计参数的收敛性。在参数估计达到收敛后，根据系统当前状态及系统实际参数，通过解有限维SOCP 问题在线生成新的标称轨迹。在此后着陆器依据该轨迹进行标称轨迹制导直到达到目标状态。

图5 参数自适应凸优化算法流程Fig.5 Parameter adaptive convex optimization algorithm

3 仿真校验

为说明本文所设计算法的有效性，本节将首先就最优观测器的收敛性及参数估计精度进行仿真校验，其次将对比分析经典的凸优化算法与本文所提出的参数自适应凸优化算法的燃料消耗及着陆精度。

3.1 参数估计

本节将利用第2 节设计的最优估计器对比冲、质量的不确定性进行估计，以验证本文所设计估计器的收敛速度及收敛精度。参考文献［1-4，33］，仿真参数设置如表1所示。

表1 着陆器仿真参数设置Table 1 Lander simulation parameter setting

表2 参数估计误差Table 2 Parameter estimation error

最优观测器对质量和比冲的估计结果如图6～图7 所示。其中图6 为着陆器质量估计曲线，由于量测值与质量直接相关，因此对质量的估计收敛很快，在0.5 s 内即收敛到了真实值，然后跟踪真实值随着飞行过程燃料的消耗而逐渐减少。相比之下，由于比冲（或质量流量系数）与量测值的导数相关，属于间接量测，所以比冲的收敛速度要慢于质量，如图7 所示。比冲大约用了10 s 才实现收敛。在本算例下，最终质量估计误差的均值为-0.005 8 kg，标准差为0.224 3 kg；最终比冲估计误差均值为0.028 6 s，标准差为0.578 s。图8 显示了协方差矩阵P的谱半径ρ(P)随时间变化情况，由于P中各元素量纲不一致，图中纵轴采用SI 单位制。可以看到随着待估计参数的逐渐收敛，P的谱半径在震荡中也逐渐减小，收敛时间不超过10 s，最终收敛值小于150。因此，在本算例给定的条件下，可取T0为10 s，ε取150作为收敛性判据。

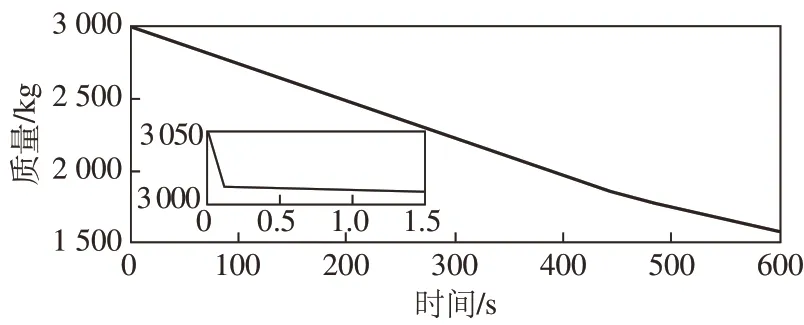
图6 质量估计曲线Fig.6 Mass estimation curve

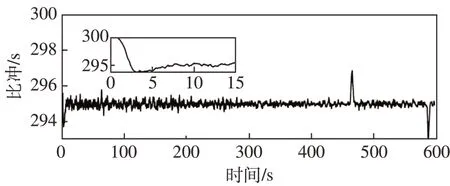
图7 比冲估计曲线Fig.7 Specific impulse estimation curve

图8 谱半径曲线Fig.8 Spectral radius curve

此外，比冲估计曲线在460 s后出现了±1.5 s 的波动，对应的谱半径曲线也出现了波动。该波动是由于推力的突然变化引起的，对应的推力曲线如图9 所示。由于推力Fc的突然变化，根据式（17），Jacobian 矩阵AJ与CJ也会发生突变，进而影响协方差矩阵P与反馈增益H(t)，并最终引起了估计值的突变。如果推力突变点出现在被估计参数收敛后，则对于着陆下降没有影响；若出现在收敛前，则图5中收敛性判据部分需要对观测器运行时间t重新计时，使得该突变的影响得以被排除，进而使得观测器有足够的时间实现收敛。一般而言，凸优化算法产生的推力曲线会产生两个推力突变点，从而引起估计值的突变。同时由图9 可以看出，采用凸优化方法后形成的推力曲线符合如式（3）描述，呈现分段恒定的特征，进而符合式（2）的推力域约束要求。

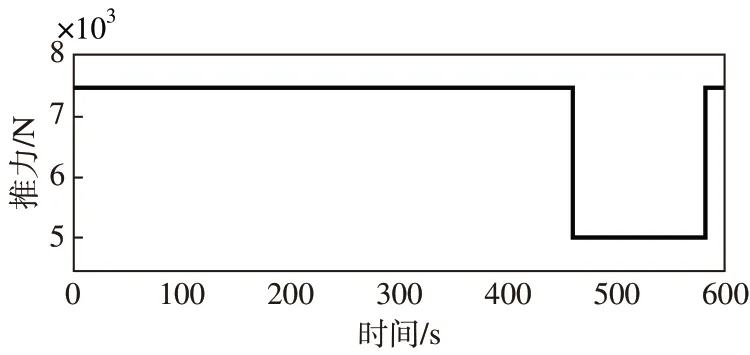
图9 推力曲线Fig.9 Thrust curve

3.2 综合仿真校验

为说明基于参数自适应凸优化的最优轨迹规划方法的有效性，本节进行了1 000 次蒙特卡洛打靶试验。分别采用经典凸优化方法，ZEM∕ZEV 制导方法，自适应凸优化方法进行着陆。仿真参数如表3所示，表3中未列举出的参数与表1保持一致。

表3 蒙特卡洛打靶仿真参数设置Table 3 Monte Carlo shooting parameter Setting

蒙特卡洛打靶结果如图10～图15所示，其中高度误差即为Z轴方向位置误差，垂直速度误差即为Z方向速度误差，相对频率为各结果对于总仿真次数的占比，对应的统计如表4 所示。由图10～图15可以看出，采用经典的凸优化算法的最终着陆点三轴位置误差分别为-33.7 m，1.4 m，16.0 m，速度误差分别为0.600 m∕s，0.016 m∕s，0.370 m∕s；采用ZEM∕ZEV 制导方案三轴位置误差分别为3.98 m，0.29 m，1.69 m，速度误差均值分别为0.050 m∕s，0.012 m∕s，0.030 m∕s；采用自适应凸优化的最终着陆点三轴位置误差分别为4.00 m，0.32 m，1.73 m，速度误差均值分别为0.060 m∕s，0.012 m∕s，0.032 m∕s。可以看到，相较于经典凸优化方法，自适应凸优化方法在很大程度上提高了速度精度与位置精度，其最终着陆精度与ZEM∕ZEV制导相当。

表4 最终着陆精度统计Table 4 Final landing accuracy statistics

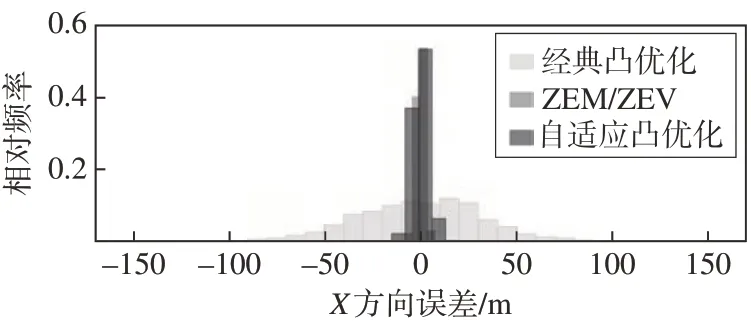
图10 X方向位置误差统计结果Fig.10 X-axis position error statistical result

图11 Y方向位置误差统计结果Fig.11 Y-axis position error statistical result

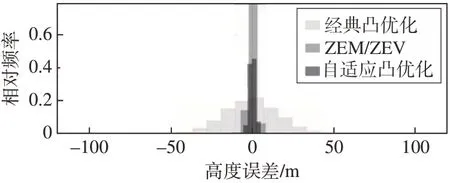
图12 高度误差统计结果Fig.12 Altitude error statistical result

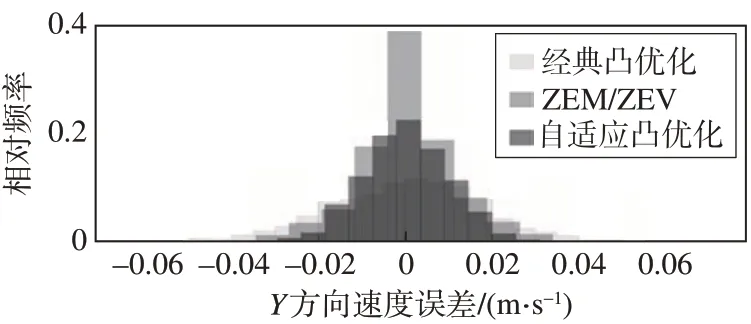
图14 Y方向速度误差统计结果Fig.14 Y-axis speed error statistical result

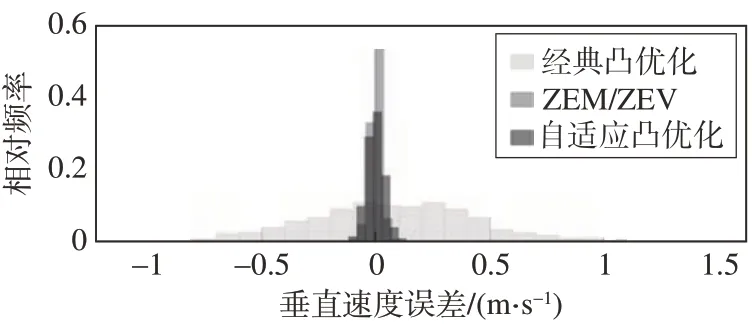
图15 垂直速度误差统计结果Fig.15 Vertical speed error statistical result

值得注意的是，无论是否采用何种制导方案，Y方向上位置，速度的精度均高于其他两轴。这是由于着陆过程中着陆器主要在航向和竖直方向运动，因此主要运动集中在纵平面内，横向运动较小，因此引起的该方向上的绝对误差也相应较小。

图16展示了1 000 次蒙特卡洛打靶的燃料消耗情况的统计结果。运用经典凸优化算法所消耗燃料的均值为1 428.9 kg，标准差为17.29 kg；采用本文所提出的参数自适应凸优化算法所消耗的均值为1 427.6 kg，标准差为16.38 kg，而采用ZEM∕ZEV 制导的燃料消耗均值为1 435.7 kg，标准差为16.50 kg。可以看出，这3 种算法所消耗燃料质量的标准差相似，这是由于所消耗的燃料分布在极大程度上取决于着陆器实际的初始质量与比冲，而这是由本仿真算例的初始条件给定的，因此其标准差几乎一致。但就均值而言，采用参数自适应凸优化算法所消耗的燃料相较于经典凸优化算法减少了2.26 kg，相较ZEM∕ZEV 减少了8.1 kg。从仿真结果可以看出，参数自适应算法相较于凸优化算法在精度提高的同时消耗燃料更少，这是由于该算在进行最优轨迹规划时采用的参数更接近于实际值，因此轨迹的最优性更好，从而更省燃料。而ZEM∕ZEV 制导算法依赖反馈调节不断接近制导目标，并未考虑参数偏差，因此虽然制导精度很高，但是燃料消耗显著多余参数自适应算法。

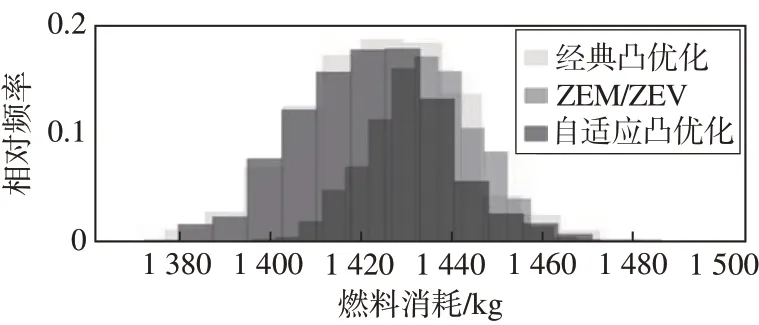
图16 燃料消耗统计结果Fig.16 Fuel consumption statistical result

图17 展示了这3 种算法在打靶运行第一次时的推力指令剖面，可以看到ZEM∕ZEV 这一定点着陆制导算法不但在某些时间段内指令推力超出了发动机的最大推力，同时其还要求发动机在一定范围内连续可调。但无论是经典的凸优化算法还是自适应凸优化算法均符合推力分段恒定的特征，满足发动机工作要求。

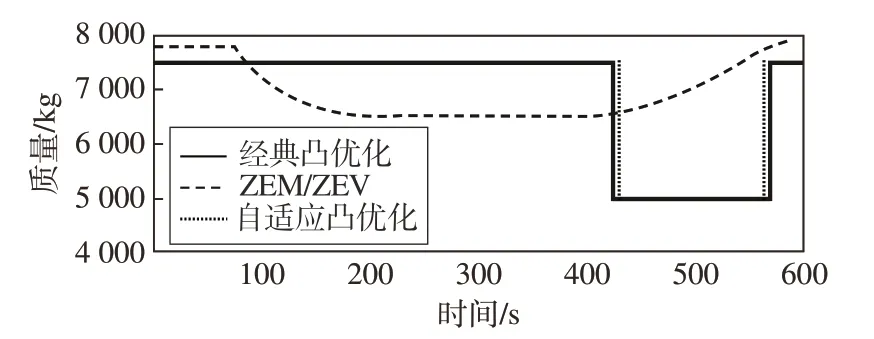
图17 典型推力指令剖面Fig.17 Typical thrust command profile

4 结论

本文提出了一种基于参数自适应凸优化的月面着陆最优轨迹设计方法。本文首先在月球着陆动力学模型的基础上将月面着陆最优轨迹设计问题转化为有限维SOCP 问题。针对该SOCP 求解过程中比冲，初始质量等参数具有一定不确定性的问题，首先利用标称参数获得最优轨迹，并在沿着该轨迹进行最优轨迹跟踪制导时，通过本文所设计的最优观测器对以上参数进行实时估计。待参数估计满足收敛性指标要求后，再将参数的估计值带入以上SOCP 问题重新求解，以此获得新的标称最优轨迹。通过对参数的实时估计以及利用该参数的估计值对月面着陆最优轨迹进行实时在线设计，使得系统对于参数不确定性具有了一定的适应能力。仿真结果表明，本文所设计的最优观测器能够完成快速收敛，实现对实时质量，比冲的在线观测。其中，在本算例下，质量收敛速度小于0.5 s，比冲收敛速度小于10 s。质量的平均估计误差小于0.23 kg，比冲估计误差小于0.6 s，极大的减小了参数不确定度。1 000 次蒙特卡洛打靶仿真表明，参数自适应凸优化算法具有推力输出剖面严格分段恒定，不需要发动机推力连续可调，仅需要发动机具有离散的推力域即可的优势；同时相较于其他算法，该算法能够在具有参数不确定性的前提下显著提升着陆精度。