基于拉格朗日乘子的交流放大电路参数优化方法
2023-12-28蒋乐群陈冰雪褚良宇李青青赵梦浩李泓钢
蒋乐群,陈冰雪,褚良宇,李青青,赵梦浩,李泓钢,洪 葳
(华中科技大学物理学院,精密重力测量国家重大科技基础设施,基本物理量测量教育部重点实验室,引力与量子物理湖北省重点实验室,湖北 武汉 430074)
交流放大电路是一种能够将特定频段的交流信号放大的电路,被广泛应用于信号放大、滤波和调制等领域,如音频放大器、无线电接收机、通信系统和医疗设备等。由于运算放大器具有增益高、稳定性好、输出线性等优点,采用运算放大器设计的交流放大电路被广泛应用于精密的空间科学测量任务中[1-2]。
交流放大电路的核心设计指标主要包括放大增益、中心频率、品质因数[3]。放大增益是交流放大电路中心频率处的放大倍数;中心频率是交流放大电路响应最强的频率;品质因数是交流放大电路带通特性以及损耗大小的重要指标。这些设计指标可以通过改变电路的元器件参数和拓扑结构等方式来优化[4-6]。交流放大电路的分析通常是建立电路的电压和电流的微分方程,从而获得电路的传递函数,对电路的元器件参数进行优化设计[7-8],或者基于Multisim等仿真软件的优化设计[9-10,13-14]。然而,电路的元器件参数通常与多个性能指标关联[11],从而给元器件参数的确定带来了一定的困难。同时,元器件参数的不连续,主要是电路中的电阻和电容值的不连续也导致电路的性能指标无法达到最优,即品质因数不能取最大值。基于此本文提出基于拉格朗日乘子法确定元器件参数从而使电路达到最大的品质因数。
1 实验原理
1.1 交流放大电路
典型交流放大电路的基本结构如图1所示。
根据基尔霍夫定律,交流放大器相关特点可以列出方程:
(1)
式中符号如图1所示,Z为相同下标的电容复阻抗,联立公式和可得传递函数,如式(2)所示。
(2)
其中,s=jω,ω为电路信号频率,j为虚数单位。
1.2 设计参数
对于交流放大电路的设计,首先需要明确中心频率和放大倍数。交流放大电路的传递函数最大值处对应的频率即为中心频率,利用柯西不等式可知:
(3)
将公式代入公式可得交流放大电路的放大倍数为
(4)
(5)
可解出两大于0的频率为
(6)
(7)
将式(6)和(7)两频率做差可得通带宽:
(8)
这时根据品质因素的定义,可以得到品质因数的表达式:
(9)
可以发现在给定中心频率,放大倍数时,品质因数随着R1和C2的增加而增加。
2 实验内容
2.1 拉格朗日函数建立
一般情况下,交流放大电路需要在给定中心频率ωs和放大倍数as下工作,同时希望品质因数尽可能地大,根据式(10)可知,在ωs、as下,品质因数只与R1和C2有关。因此,将中心频率与放大倍数视为约束,同时将品质因数的优化问题转化为在两完整约束下求函数极大值的问题,故使用拉格朗日乘子法,写出拉格朗日函数:
(10)
其中,α和β为拉格朗日乘子,将其写成隐式的形式以简化计算:
L=R1C2aω+α(a-as)+β(ω-ωs) 。
(11)
2.2 极值点求解
对拉格朗日函数求偏导并使其为零可得:
(12)
(13)
(14)
(15)
(16)
(17)
(18)
联立公式,可解出:
(19)
因此,品质因数可写为
(20)
这时,可以得出结论:在需要的中心频率和放大倍数下,为了得到最大的品质因素,需要取最小的R2,尽量大的R3以及与R3成1/(2as)倍的R1,相等的C1和C2。
3 数值计算
以中心频率为50 kHz,放大倍数为3的交流放大电路设计需求为例来进行验证论文提出的方法。将设计需求代入公式和可以得到:
(21)
为了进一步探究品质因数达到最大值时各参数之间的关系,分别在各参数空间进行绘图。电容电阻器件选择范围为:电容5.00×10-13~1.00×10-6F、电阻1~1.00×10-6Ω。首先在中心频率与放大倍数的约束下,确定品质因数与R2关系,这时任意选定R1,不失一般,选取R1=1 Ω,如图2所示。从图中可以看出品质因数随R2的增大而单调减小,故将R2的取值定为参数空间内最小值,即R2=1 Ω。
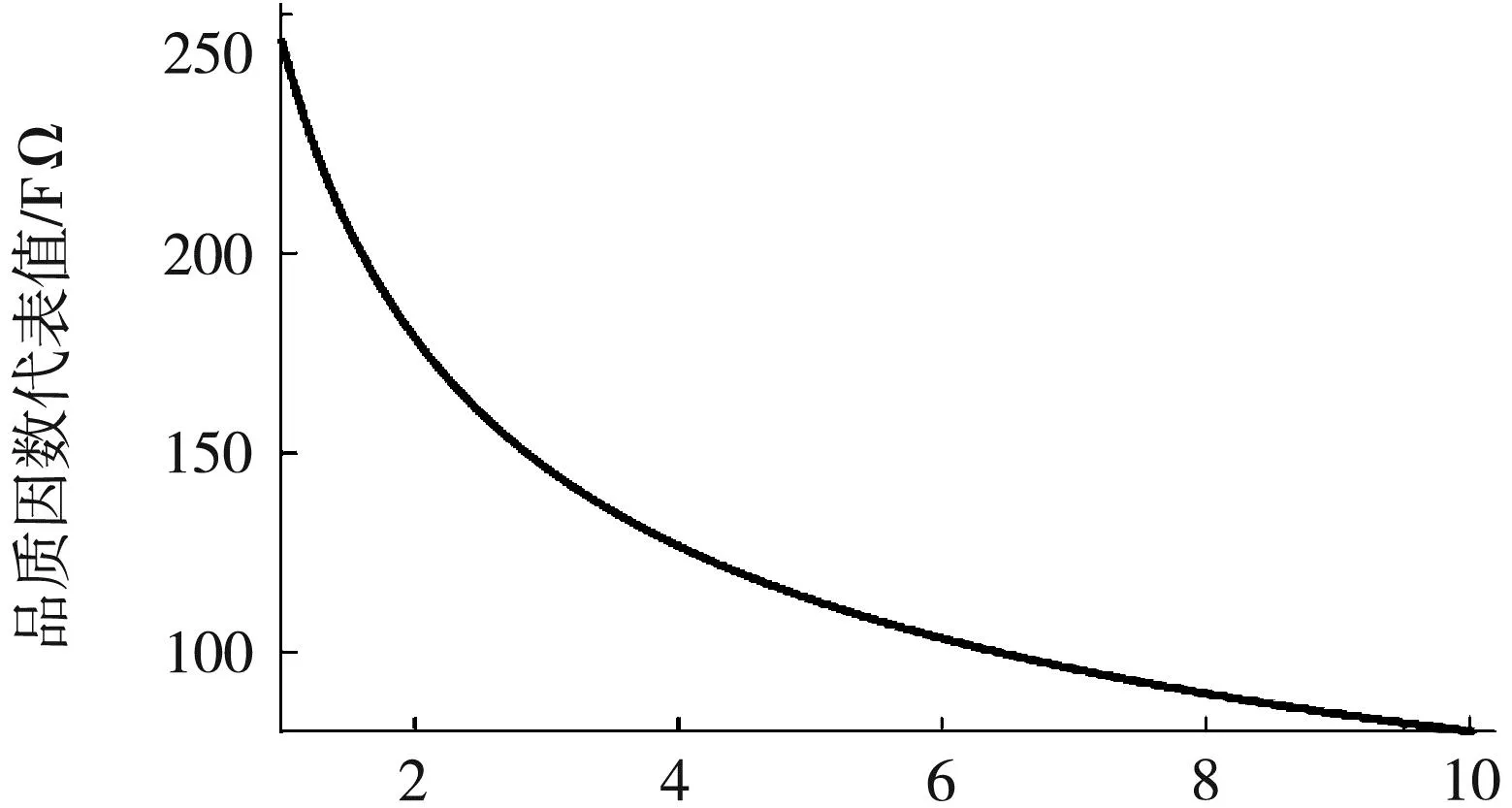
图2 品质因数代表值与R2关系
确定了R2=1 Ω之后,在此条件下,接着讨论R1,C2、R1,R3和C1,C2分别满足何种关系时品质因数可以达到最大值。选取R2=1 Ω绘制图3至图5,图3是参数空间内品质因数与R1,C2的关系图,图4是参数空间内品质因数与R1,R3的关系图,图5是参数空间内品质因数与C1,C2关系图。从以上各图可以看出,品质因数Q随R1,C1的增大而增大,在图4和图5的空间中,品质因数最大值分别各在一条曲线上,经确认这两条曲线分别为R3=6R1、C1=C2,与理论计算的公式值一致,进一步说明品质因数最优值应在理论计算的超平面上。

图3 品质因数Q与R1,C2的关系图
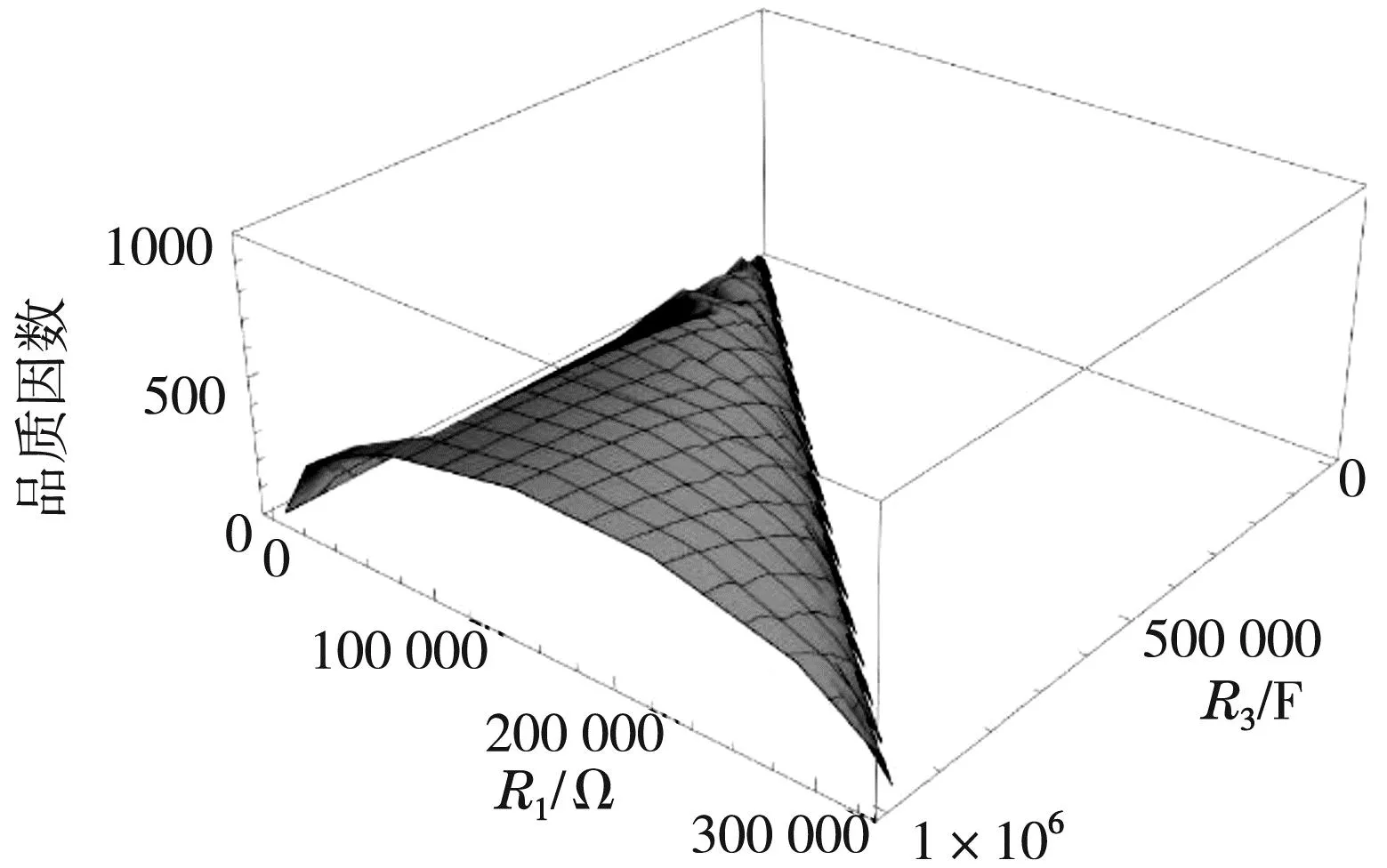
图4 品质因数Q与R1,R3的关系图
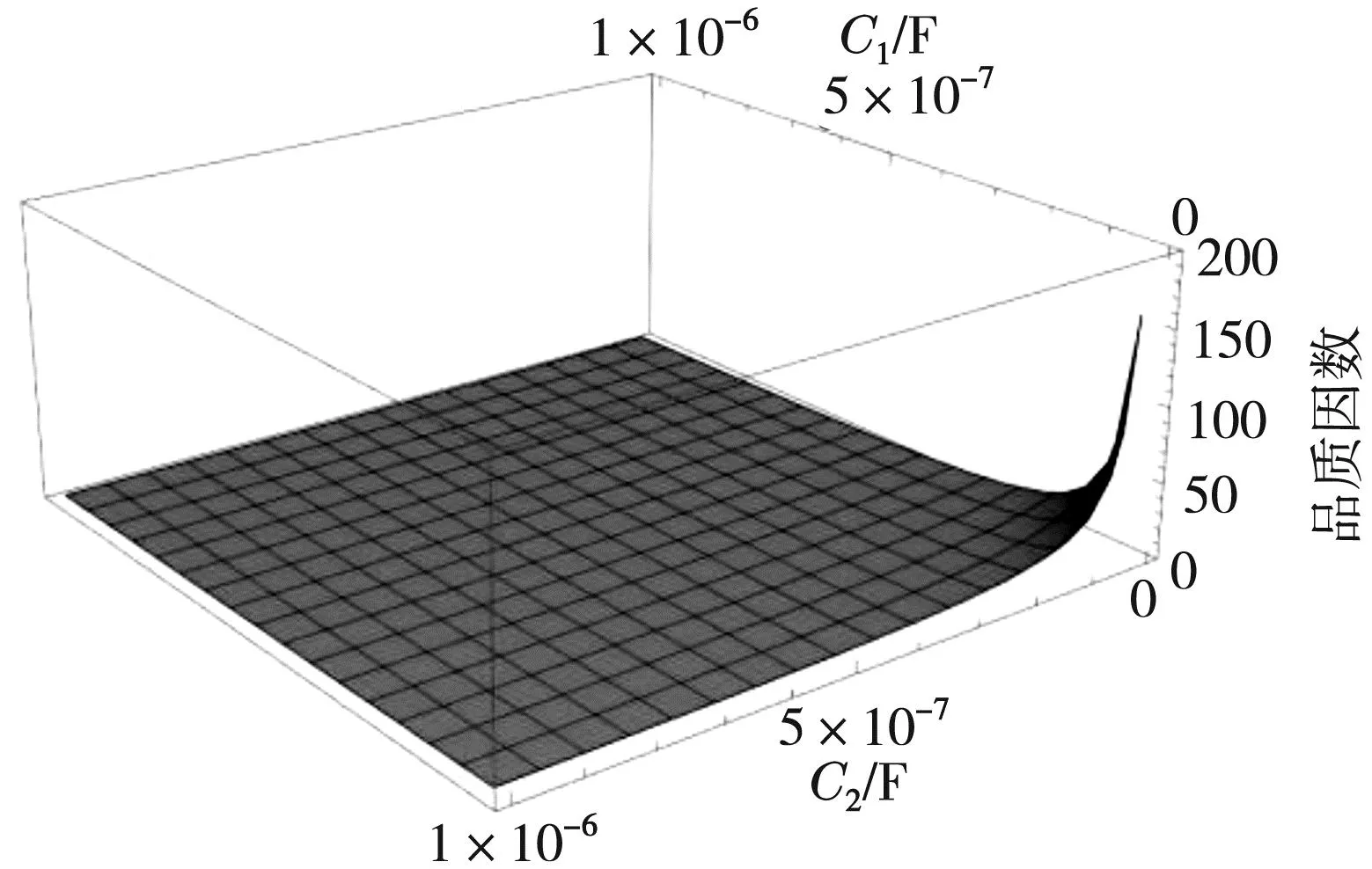
图5 品质因数Q与C1,C2的关系图
最后在给定器件参数空间中进行遍历,以对比理论给出的结果。由于中心频率与放大倍数给定时,品质因数可以直接通过R1C2求出,为减小计算量以品质因数代表值R1C2来评价品质因数,遍历结果如图6所示。
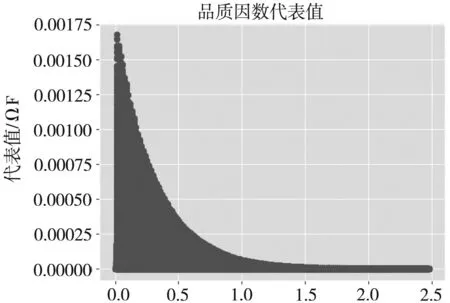
图6 品质因数代表值
最大代表值处的器件参数如表1所示。

表1 遍历最优值参数表
使用该组参数计算品质因数,再根据理论预言计算关键数据有:
(22)
虽然由于器件取值的非连续性,关键数据与理论之间存在一定出入,然而在考虑器件非连续性带来的误差的允许范围内与本文的理论模型一致,这足以表明本文理论的正确性。
4 仿真验证
考虑到实际使用的运算放大器不是理想运算放大器,因此为了保证虚短和虚断条件成立电阻R2不能太小,因此将R2限制为不能小于1 kΩ,并依据提出的约束条件,给出可行参数如表2所示。为了验证参数的正确性,使用Multisim14.0进行仿真验证[12]。

表2 最优值参数表
仿真结果如图7(a)所示,可测的此参数条件下品质因数Q为

(a)
Q=15。
(23)
同时为了确定表2中的选取的参数是参数选取范围内最优参数,在满足放大倍数和中心频率设计要求的情况下,另外设计四组不同参数,仿真其波特图,如图7(b)~(e)所示。
对式(23)中参数与其品质因素进行汇总对比,如表3所示。可以看出虽然这五组参数都达到了预期的放大倍数和中心频率,但本论文提出的优化方法获得的品质因数具有明显的优势,由此说明所提出的优化方法的有效性。
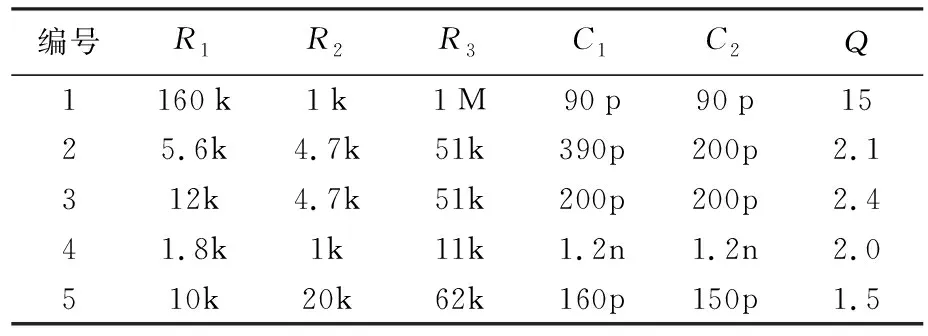
表3 不同参数品质因数
5 结 论
本文提出了一种基于拉格朗日乘子的交流放大电路参数优化方法。首先采用基尔霍夫定律推导出典型交流放大电路的传递函数;随后通过建立拉格朗日函数讨论了使用拉格朗日乘子来求解在给定中心频率和放大倍数下品质因数的最大值问题;最终通过理论参数遍历和仿真实验验证了优化方法的有效性。
通过对交流放大电路的系统阐述,本文为设计和研究交流放大电路提供了理论基础。研究结果可以帮助工程师优化电路的性能,提高设计精度。
