Dynamic analysis of bio-inspired helicoid laminated composite plates resting on Pasternak foundation excited by explosive loading

Ngoc-Tu Do ,Quoc-Ho Phm

a Faculty of Mechanical Engineering, Hanoi University of Industry, Hanoi, Viet Nam

b Faculty of Engineering and Technology, Nguyen Tat Thanh University, Ho Chi Minh City, Viet Nam

Keywords:Isogeometric analysis Pasternak foundation Dynamic response Laminated composite

ABSTRACT This paper uses isogeometric analysis (IGA) based on higher-order shear deformation theory (HSDT) to study the dynamic response of bio-inspired helicoid laminated composite (B-iHLC) plates resting on Pasternak foundation (PF) excited by explosive loading.IGA takes advantage of non-uniform rational Bspline(NURBS)basic functions to exactly represent the structure geometry models and the attainment of higher-order approximation conditions.This method also ensures a C1 continuous function in the analysis of transverse shear deformation via HSDT.Furthermore,IGA eliminates the requirement for correction factors and delivers accurate results.Pasternak foundation with two stiffness parameters:springer stiffness (k1) and shear stiffness (k2).The derivation of the governing equations is based on Hamilton's principle.The proposed method is validated through numerical examples.A comprehensive analysis of the impact of geometrical parameters,material properties,boundary conditions (BCs),and foundation stiffness on dynamic response of B-iHLC plates is carried out.

1.Research problem overview

Nature is remarkable in its ability to create structures that can efficiently handle loads with minimal stress and deformation and are capable of withstanding high-impact forces.There are many studies demonstrating nature's superior structures that humans can apply in design and manufacture.Some works study sandwich structures with a honeycomb core based on the idea of following the honeycomb structure in nature [1-3].Besides,the layering configurations observed in various natural structures such as plants,insects,and animals result in increased stiffness.By adopting these configurations in laminated structures,it is possible to attain high stiffness without sacrificing toughness [4-6].Researchers are exploring the design and manufacture of hierarchical structures that are inspired by natural materials such as spider webs,shells,bones,and leaves.The goal is to create new materials with properties and functions that are similar to those found in nature.By mimicking the hierarchical structures of biological materials,researchers aim to develop materials with high strength,toughness,and stability,as well as low weight and improved sustainability [7-9].Its helical or Bouligand structure,composed of chitin,effectively dissipates energy,prevents the growth of cracks,and provides high stiffness [10].Inspired by the helical arrangement of layers in laminated composite structures,researchers have investigated the impact of foreign objects on these structures[11-16].The superiority of the helical layup is evident in the work of researchers like Liu et al.[17],who demonstrated its selfrecoverability capacity.Yin et al.[18] have also studied the toughening mechanism in helicoidal plates inspired by the anatomy of coelacanth fish.Fig.1 illustrates various biological sources from which helical structures can be derived.

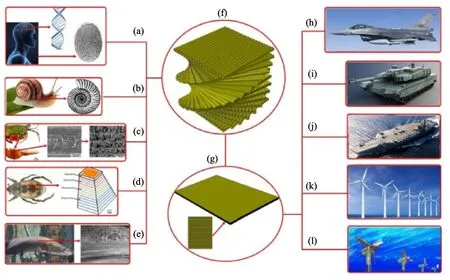
Fig.1.Bio-inspired helicoidal structure:(a)Fingerprint and DNA;(b)Snail shell;(c)Helicoidal fiber organization of Odontodactylus scyllarus[19];(d)The exoskeleton of a beetle;(e) Collagen fibril lamellae from Arapaima gigas scales [20];(f) The Bouligand helicoidal structure is inspired by (a)-(e) these biological structures and can be used to design (g)composite laminates.The potential applications of these bio-inspired helicoidal composite laminates include anti-low velocity impact or anti-bullet products for (h) warcraft,(i)tanks,and (j) warships,as well as energy applications such as (k) wind and (l) hydraulic turbine blades.(Adapted with permission of Jiang et al.[21] from Elsevier).

There are many review articles in the literature that summarize the work done on the analysis of laminated composite plates,beams,and shells under various loading conditions.Reddy [22]published an extensive review of shear deformation theories and their origins for the analysis of laminated structures.Carrera [23]reviewed the available zigzag theories in the literature for analyzing laminated composite and sandwich structures.Zhang and Yang [24] published a review of finite element-based analysis of laminated structures.Liew et al.[25]reviewed various meshless methods for analyzing laminated structures.Mohamed et al.[26]presented the review of the mechanical behavior of bio-inspired composite plates.Zhang et al.[27]predicted the bending resistance of basalt fiber laminate composite with a bionic helical structure.Almitani et al.[28] provided exact solutions for the bending and buckling analysis of B-iHLC beams supported on PF.Garg et al.[29]conducted a study of the free vibration and buckling analysis of BiHLC plates using a higher-order zigzag theory.Furthermore,readers can find different methods for analyzing the mechanical behavior of composite plates in Refs.[30-32].

Studying the mechanical behavior of structures lying on elastic foundations (EFs) has typical works as Guellil et al.[33] presented the influences of porosity distributions on the mechanical bending response of functionally graded plates resting on EFs using Navier solution.Hadji et al.[34]analyzed the influence of porosity and EF on the bending behavior of sandwich structures.Zaitoun et al.[35]examined the vibration of a functionally graded (FG) sandwich plate resting on the viscoelastic foundation based on the accurate high-order shear deformation theory (HSDT).In addition,the hygro-thermo-mechanical bending and vibration response of FG plates resting on EFs is introduced in Refs.[36,37]and the influence of the visco-Pasternak foundation parameters on the mechanical behavior of FG sandwich plates is presented in Refs.[38,39].Besides,the results on the effect of the elastic foundation on the mechanical response of plates can be provided in Refs.[40-42].

To overcome the limitations of classical FEM and analytical methods for computing the complex structures,Hughes et al.[43,44] introduced the IGA method based on computer-aided design (CAD).The effectiveness of IGA has been demonstrated in various studies [45-53].IGA can be implemented on computers with open access to the internet.Since then,many researchers have applied IGA to structural analysis using different plate theories.For example,Valizadeh et al.[54] used IGA with the first-order shear deformation theory (FSDT) to analyze the bending,vibration,and flutter of functionally graded materials(FGM)structures.Natarajan et al.[55]studied the non-local free flexural vibration of FGM plates using IGA with a third-order NURBS basis function.Anitescu et al.[56] analyzed electrodynamics using IGA based on a dual-basis diagonal mass formulation.The advancement of IGA is that it is possible to solve mathematical models with the C1 continuity problem without requiring any additional variables or Hermite interpolation functions.The basic idea of IGA is to use elementary functions to accurately describe the geometric domain as well as to approximate unknown fields.Since the geometric domain is modeled correctly and the number of variables does not increase.It hence motivates us to employ IGA based on HSDT for analysis of BiHLC plates subjected to explosive loading.

Explosive loading is a type of short-term load with great intensity,dangerous to weapons,equipment and people,so the study of structures subjected to this loading is necessary.Based on the study of Khdeir et al.[57],the sinusoidally explosive loadingp（t）is a type of short-term load that can be caused by various sources,such as explosions,supersonic projectiles,or rockets that operate nearby acting perpendicular (z-direction) to the surface of plates.This type of loading can be mathematically described by the function.

in whichts=0.006 s,γ=330 s-1,q0=68.9476 MPa;aandbare the length and width of composite plates,respectively(see Fig.2).

Fig.2.The model of the B-iHLC plate resting on Pasternak foundation.

Several studies have been conducted to investigate the mechanical behavior of structures subjected to explosive loading,and some typical works are Refs.[58-61].More recently,Duc et al.[62,63] analyzed the nonlinear vibration of Functionally Graded Material (FGM) plates under blast loading,while Qi et al.[64]investigated the forced vibration of curved sandwich panels subjected to explosive loading.It is worth noting that all the aforementioned studies employed analytical solutions to examine the response of the structures under consideration.

Through the evaluation of the results achieved,it can be observed that IGA in combination with HSDT is very suitable for analyzing structures and provides high accuracy.Thus,the novelty of this work is the implementation of a finite element formulation based on IGA and HSDT for dynamic analysis of B-iHLC plates located on PF excited by explosive loading.Moreover,the new numerical results on the influence of geometrical,material,and EF on the dynamic analysis of B-iHLC plates are provided in detail.The authors believe that this study will be an important basis for scientists to apply to research and design military equipment such as tanks,armored vehicles,missiles,submarines,combat aircraft,and so on.

Besides the introduction,this paper is composed of five sections.In section 2,the authors delve into geometrical models,elastic foundations,and thermal environments.Section 3 presents a comprehensive derivation of the motion equation for B-iHLC plates.To validate the proposed method,the authors conduct numerical simulations and present the results in section 4.Finally,section 5 concludes the paper by summarizing the key findings.

2.Geometrical model and material properties

In this study,three different helical designs,namely the helicoidal-recursive (HR),helicoidal exponential (HE),and helicoidal-semicircular (HS) are analyzed.Fig.3 displays an isometric view of these configurations,which are summarized in Table 1.

The plate resting on PF includes springer stiffness(k1)and shear layer stiffness (k2) can be determined as follows [65]:

The Pasternak foundation model is a two-parameter model that describes the foundation reaction as a function of the deflection and its Laplacian.The negative sign in front of the second term indicates that the shear resistance is opposite to the direction of curvature [66].This means that when the deflection is concave upward,the shear resistance is downward,and vice versa.The negative sign also ensures that the total foundation reaction is zero when there is no deflection.

3.Theory and formulation

3.1.Higher-order shear deformation theory (HSDT)

The displacement field following HSDT is expressed by [67]

whereu0,v0,θx,θy,andware displacement variables.f（z）=z（1-4z2／3h2）is the continuous function [68].

Then,the strain-displacement relations are defined by

withf′（z）is the derivative of the functionf（z）.

In which

The stress resultants are calculated as follows:

with A，B，Bb，F，Fband H are defined by

where

with α is the fiber angle of theklayer.

Replacing Eq.(8) into Eq.(7),authors get

3.2.The governing equations of FGP plates

In the realm of classical mechanics,Hamilton's principle is a variational principle that asserts that the motion of a system is determined by minimizing the action functional.This action is computed by taking the integral of the Lagrangian over time,where the Lagrangian represents the difference between kinetic and potential energy.The subtraction of potential energy from kinetic energy is denoted by a negative sign in the equation[69].

where,the virtual strain energy is

The virtual work done by the transverse forces is

The virtual deformed elastic foundation is

The virtual kinetic energy is (see Appendix A for details):

where L is expressed by

in there

where

with ρ is the mass density,and

The weak form for the vibration of plates is expressed by[69]

3.3.Isogeometric analysis

In this study,the displacement field is approximated by the NURBS functions as follows [47]:

where dK=｛u0Kv0K wKθxKθyK｝Tis the displacement of control pointK,and RKrepresent the shape function [44].

Substituting Eq.(26) into Eq.(6),we have

in which

Substituting Eq.(27)into Eq.(25),the motion equation of plates is

where,the stiffness matrix is

The mass matrix is

The foundation stiffness matrixis

The transverse load vector is

Now,the motion equation of FGP plates is defined by

If the force vector is a time function F=F（t）and takes into account the structural damping,Eq.(40) is rewritten by

in which C=αM+βK,with α and β are Rayleigh damping factors defined through damping ratio ζ and the first two natural frequencies[69].

To solve Eq.(41),the authors use the Newmark method with the steps presented in Appendix B.This paper focuses on IGA,where boundary conditions(BCs)are determined based on the geometric constraints at the edges.The BCs used in this study are denoted and presented as follows:

-Clamped(C):

-Simply supported (S):

-Free support(F):at the boundary edge,all degrees of freedom(DOFs) are non-zero.

4.Numerical results

4.1.Verification

Example 1: the outcomes reported by Mohamed et al.[26] are utilized to validate the current model on the free vibration analysis of B-iHLC plates.For this illustration,a composite plate consisting of 32 layers of linear helicoid ([0/24/48/72/96/120/144/168/192/216/240 …/360]s) and Fibonacci helicoidal [0/10/10/20/30/50/80/130/210/340/190/170/360/170/170/340]s) is employed.The utilized material properties areE1／E2=10,G12=G13=0.5E2,G23=0.2E2,ν12=0.25,ρ=100.The results obtained in the current method and those reported by Mohamed et al.[26] are listed in Table 2It is noticeable that the current results match well with previous findings.The discrepancy between the current results and those reported by Mohamed et al.[26] is due to the adoption of FSDT by the latter authors within the differential quadrature method(DQM)framework.The results of the proposed method converge at a mesh size of 11× 11.As a result,the same mesh size will be employed in future investigations.

Table 2 Convergence and validation study.

Example 2: The SSSS square laminated plate sorted as [0/90/0]with geometrical dimension:h=0.1524 m;a=b=5his considered.The utilized material properties are:E1=172.369 GPa,E2=6.895 GPa，G12=G13=3.448 GPa,G23=1.379 GPa,ν12=0.25,ρ=1603.03 kg／m3.The plate is subjected to a sinusoidally distributed transverse load including triangular loads as

in whichts=0.006 s,γ=330s-1,q0=68.9476 MPa.As shown in Fig.4,the central displacement of the composite plate is compared to the precise solutions calculated by Khdeir and Reddy [57] using HSDT.The central deflection graph is in close agreement,with the difference between the current results and the exact solutions being minimal and acceptable.Based on the above examples,it can be concluded that the proposed method is suitable for the vibration analysis of composite plates.Note that,in this study,the cubic Bspline basis functions are applied.

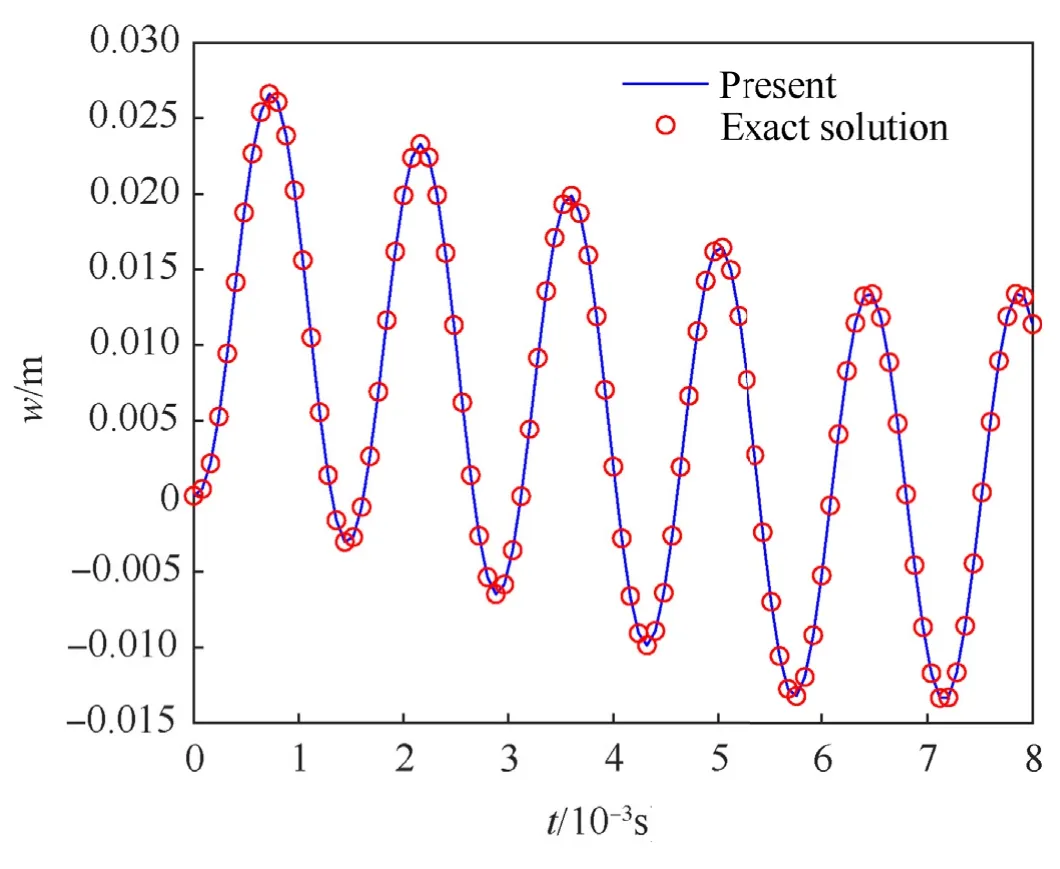
Fig.4.The time history analysis of SSSS composite square plates.

4.2.Free vibration problem

Firstly,the SSSS 20-layered HR1 square plate with geometric dimensionsa=b=1 m,h=a／50 and the material properties as shown in example 2 of subsection 4.1.The composite plates resting on PF with the foundation stiffness get valuesk1=0.1 GPa／m andk2=0.01 GPa·m.The first six mode shapes of the composite plate are plotted in Fig.5.It can be seen that it seems that the second and third-mode shapes are similar,as expected.The difference is due to the direction of view since the square plate is simply supported on four sides.

Fig.5.The mode shapes of the SCSC FGP square plate:(a)Mode 1,f1=497.0727 Hz;(b)Mode 2,f2=693.4083 Hz;(c)Mode 3,f3=769.1244 Hz;(d)Mode 4,f4=917.3449 Hz;(e)Mode 5, f5=946.3468 Hz;(f) Mode 6, f6=1128.356 Hz.

Fig.6.The effect of helicoidal schemes on the dynamic response of SSSS B-iHLC plates(12 layers) without damping ratio（ζ=0）: (a) The deflection response at the plate center point;(b) The stressσx via thickness at t=0.001 s;(c) The stressvia thickness at t=0.001 s.

Fig.7.The effect of helicoidal schemes on the dynamic response of SSSS B-iHLC plates(12 layers)including damping ratio（ζ=0.08）:(a)The deflection response at the plate center point;(b) The stress via thickness at t=0.0025 s;(c) The stressvia thickness at t=0.0025 s.

Secondly,Table 3 reports natural frequencies for different helicoidal schemes,foundation stiffness（k1，k2）and length-tothickness ratio（a／h）of SSSS composite plates with 24 layers,while Table 4 lists natural frequencies of SCSC composite plates with 16 layers.From these tables,it can be seen that the helical diagram effect has a significant influence on the free vibrations of composite plates,the increase or decrease of the natural frequency depends not only on the number of layers but also on the parameters β，γ，φ and χ.As expected,a thicker plate demonstrates greater stiffness and,as a result,has a higher natural frequency.Additionally,the PF improves plate stiffness,which raises the natural frequency.In addition,it is clear that the shear layer(k2)offers stronger support than the springer layer (k1).

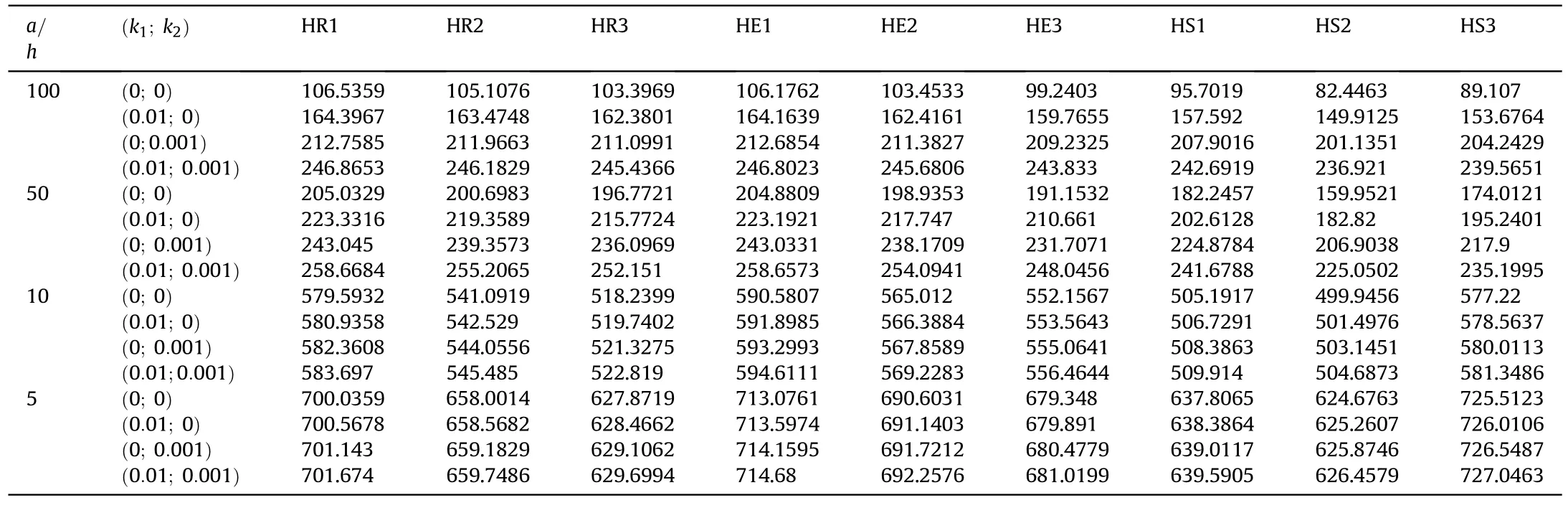
Table 4 The natural frequency for SCSC B-iHLC plates with 16 layers via helicoidal schemes,foundation stiffness（k1，k2）and length-to-thickness ratio（a／h）.

Thirdly,the effect of the number of layers (NOLs) on free vibration of B-iHLC is considered.The dependency of natural frequency over NOLs can be observed in Table 5 and Table 6.When increasing NOLs,no clear trend regarding the variation in the value for the natural frequency is observed.For instance,for the CCCC boundary condition,the natural frequency increases and decreases for the remaining configurations as the number of layers increase for the HS3 configuration(observe Table 5).For the SSSS boundary condition,the natural frequency decreases and then increases with an increase in the number of layers with HR2,HR2 and HE2 configurations.Whereas for the HR1 and HS1 configurations,the natural frequency decreases with an increase in the number of layers;vice versa for HS2 and HS3 configurations.HE1 and HE3 configurations,the natural frequency changes don't follow any rules(observe Table 6).Herein,a／h=5，10 is the thick plate whilea／h=50 anda／h=100 correspond to the moderately and thin plate,respectively.

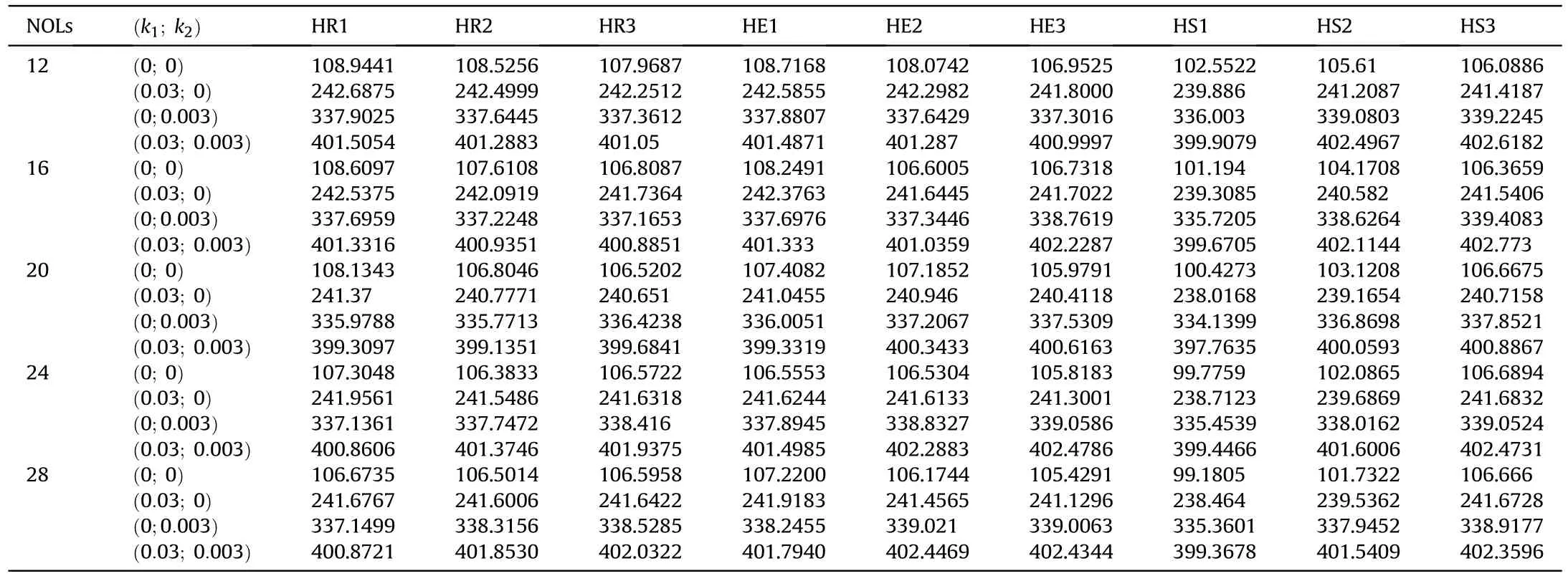
Table 5 The natural frequency for CCCC B-iHLC thin plates(a／h=100) via number of layers.

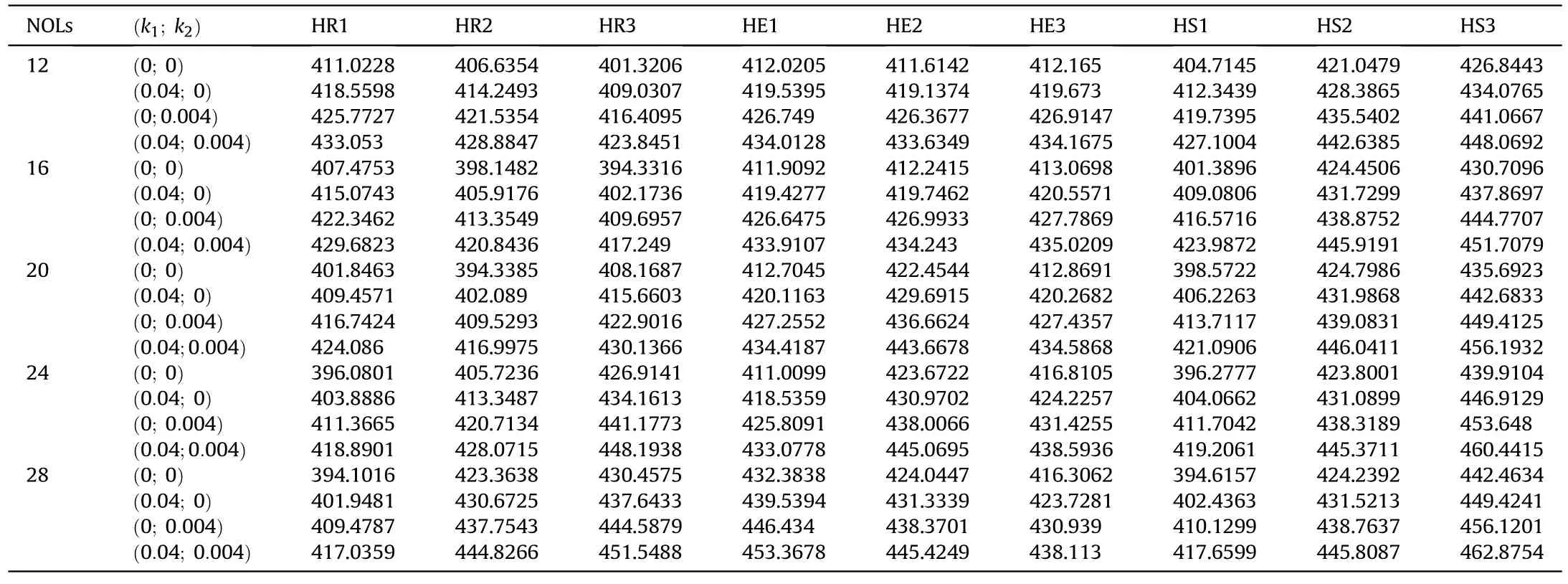
Table 6 The natural frequency for SSSS B-iHLC thick plates(a／h=10) via number of layers.

4.3.Forced vibration problem

In this section,the authors examine the vibration characteristics of B-iHLC plates subjected to the sinusoidally explosive loading as defined in Eq.(1).The structural parameters will be completely displayed on each figure for the reader's convenience.The material properties of B-iHLC plates are provided in Example 2 of subsection 4.1.

Firstly,the effect of the helicoidal schemes on the forced vibration of SSSS B-iHLC square plates without damping ratio（ζ=0）and including damping ratio（ζ=0.08）are displayed in Figs.6 and 7,respectively.It can be seen that the B-iHLC plate with the HS3 configuration has the greatest stiffness resulting in the smallest displacement response.In contrast,the B-iHLC plate with the HS1 configuration results in the greatest displacement response by providing the smallest stiffness.In addition,the stress response along the plate thickness has a jump due to delamination in the laminated composite structure.It is obvious that the stress curve of the B-iHLC plates is smoother than that of the conventional laminated composite plates.The smoothness of the stress curve depends on the number of layers and the helicoidal configuration.Moreover,the B-iHLC plate will oscillate gradually if structural damping is included.Secondly,Fig.8 presents the impact of NOLs on the vibration characteristic of CCCC HR2 square plates without damping ratio（ζ=0）.Observing this figure,we can see that the deflection response of HR2 plates with 20 layers is the largest and the smallest with the 28 layer HR2 plates.This proves that with the same thickness,the HR2 plates with 28 layers is the hardness and the softest in case of HR2 plates with 20 layers.Note that,the responses of the plate are separated into two phases.In the first phase,the plate is forced vibration due to being subjected to transverse loads.And in the second phase,the plate is free vibration,i.e,the vibration of the plate is harmonic.

Finally,Fig.9 displays the impact of NOLs on the vibration characteristic of SCSC HE2 square plates without damping ratio（ζ=0）.Observing that the deflection response of HR2 plates with 28 layers is the largest and the smallest with the 12 layers HR2 plates.This proves that with the same thickness,the HE2 plates with 12 layers is the hardness and the softest in the case of HR2 plates with 28 layers.As expected,the displacement (w) and stress (σx)response curves versus time are congruent.

Fig.9.The effect of the number of layers(NOLs)on the dynamic response of SCSC HE2 square plates including damping ratio（ζ=0.1）:a)The deflection response at the plate center point;(b)The stress response at the plate center point;(c)The stressvia thickness at t=0.0025 s.

5.Conclusions

This paper aims to present the free and forced vibration behavior of B-iHLC plates having different helicoidal schemes.The analysis is carried out using the IGA-based HSDT in the framework of Hamilton's equation.The validation study is carried out by comparing the present results with those available in the literature.The effects of the material properties,geometric properties,BCs,and helicoidal layup scheme are carried out in detail.The important findings from the present study are:

· The choice of the helical scheme has a significant impact on the vibration behavior of the helical B-iHLC plates.

· The boundary conditions also play a vital role in determining the vibration behavior of composite plates.

· The number of layers significantly affects the vibration response of B-iHLC plates,depending on boundary conditions and different helicoidal schemes will lead to different behaviours.

· IGA is a modern numerical method that provides high convergence and accuracy while satisfying the majority of higher-order plate theories.

· The numerical results are expected to be useful for the design and fabrication of composite plates in military equipment such as tanks,armored vehicles,missiles,submarines,combat aircraft,etc.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A

The virtual kinetic energy is

Appendix B

The steps of the Newmark-beta method to solve Eq.(41) as follows:

Step 1.Defining the initial conditions.

in which α，γ are determined by assuming that the acceleration varies linearly in each integral step.

With the convergence condition,

Step 3.Determining the effective stiffness matrix and the nodal force vector,

Step 4.Determining the nodal displacement vector ut+Δt,

Repeating the loop until the finish.