电动助力转向系统的鲁棒H∞控制研究

赵 歆，唐 岚

（西华大学汽车与交通学院，四川 成都 610039）

1 引言

电动助力转向（Electric Power Steering，简称EPS）系统是根据控制策略实时提供合适的转向助力矩，可提高车辆的操纵稳定性、乘坐舒适性和安全可靠性。EPS系统已在汽车转向系统中广泛使用［1］。但在建立EPS系统数学模型时，存在模型参数的不确定性、传感器测量偏差、路面干扰等影响着EPS的性能。为提高EPS的转向性能，其控制方法研究逐渐从传统控制理论转向现代控制理论，同时越来越多的企业和学校将鲁棒控制方法运用到EPS控制研究中。

文献［2］提出了双控制器结构，分别采用H2和H∞设计方法，解决了电机转矩和转向运动的问题；2015年文献［3］提出了一种基于PI观测器的P-EPS系统驱动转矩估计方法，设计混合H∞/H2控制器；文献［4］为提高车辆横向稳定性，设计了一种基于前轮主动转向系统的鲁棒H∞输出反馈车辆偏航控制；文献［5］以良好的转向路感、转向鲁棒稳定性等为控制目标，结合H∞控制和H2控制两种方法，设计了混合H∞/H2控制器；文献［6-7］针对EPS中存在的模型不确定性和路面干扰等问题，提出了用遗传算法求解最优权函数和鲁棒H∞控制器；文献［8］针对线控转向中驾驶员的特性参数的不同，设计了一种车辆路径跟踪鲁棒控制器，实现个性化驾驶。

以某微型电动汽车的EPS为研究对象，在电压补偿控制的基础上，忽略转向系统机械结构参数的变化，针对传感器噪声和路面干扰，设计出一个基于电压补偿的EPS系统鲁棒H∞控制器，并利用MATLAB/SIMULINK仿真对比了电压补偿控制和基于电压补偿的鲁棒H∞控制的转向性能。

2 数学理论模型

2.1 电动助力转向动力学模型

EPS系统根据电机不同的助力位置分为C-EPS（转向轴型）、G-EPS（转向齿轮型）和R-EPS（转向齿条型）［9］。以转向轴式齿轮齿条电动助力转向为研究对象。齿轮齿条式电动助力转向主要由方向盘、转向轴、电机、控制器、转矩传感器、齿轮齿条转向机构等组成［10］。只考虑系统的转动惯量、阻尼和摩擦，不考虑系统的非线性因素，可将系统简化为以下四个受力部件［11］。其简化后的结构图，如图1所示。对应数学微分方程如下：

图1 电动助力转向简化结构图Fig.1 Simplified Structure Diagram of Electric Power Steering

（1）方向盘转向轴：将方向盘和转向轴看成一个刚性结构，驾驶员施加扭矩Th给方向盘，其扭矩经过转向轴向下传递力，同时方向盘会受到转向轴的反向阻力矩。

式中：Th—驾驶员的操纵力矩（N·m）；Ts—扭矩传感器测量值（N·m）；Jh—方向盘与转向轴的转动惯量（kg·m2）；Bh—方向盘与转向轴的阻尼系数（N·m·s/rad）；θh—方向盘转角（rad）。

（2）扭矩传感器：扭矩传感器安装在转向轴上，通过检测两端的转角差值，再乘以传感器等效扭杆刚度系数即可得到扭矩传感器测量的扭矩。

式中：Ks—扭矩传感器的刚度系数（N·m·s/rad）；

θp—转向齿轮转角（rad）。

（3）助力电机：采用简单的直流电动机模型。将电机内部简化为一个电阻和一个电感串联的电枢，由Kirchhoff电压定律，可以得到电机电枢回路的微分方程（3）；电机电磁转矩与电流成正比，如式（4）所示；电机输出的转矩经过减速器传递至下方转向系，可以将电机输出轴与减速机构视为一个整体，最终传递到转向系的助力转矩Ta通过受力分析，如式（5）所示。

式中：Tm—助力电机电磁转矩（N·m）；Ta—助力电机助力力矩（N·m）；Jm—助力电机转动惯量（kg·m2）；Bm—助力电机阻尼（N·m·s/rad）；Ka—助力电机转矩常数（N·m/A）；Km—助力电机刚度系数（N·m·s/rad）；N1—减速器减速比。

（4）齿轮齿条转向系：齿轮齿条转向系通过齿轮齿条将轴的旋转运动转化成齿条的横向运动，从而带动车轮偏转。转向轴输出力矩与助力电机提供的辅助力矩一起作用于齿轮齿条结构，同时需要克服转向阻力矩。通过受力分析可得：

式中：Jr—齿轮上等效惯性矩（kg·m2）；Tr—齿轮上的等效阻力矩（N·m）；Br—齿轮上的等效阻尼系数（N·m·s/rad）；Kc—齿轮上的等效刚度（N·m·s/rad）。

2.2 轮胎数学模型

汽车在转向的过程中，由于路面侧向倾斜、侧向风、曲线行驶的离心力等作用，轮胎中心会受到侧向力，侧向力使轮胎与接地印迹中心产生侧偏角，侧偏力与侧偏角成正比关系，其作用点在轮胎拖距处，使得轮胎平面绕转向主销产生转向阻力矩［12］。由于转向齿轮与前轮在机械结构上具有一定的传动比，因此在转向齿轮处产生的转向阻力矩公式如下：

式中：N2—小齿轮与前轮转角传动比；θf—前轮转角（rad）；β—车辆行驶过程中的车身侧偏角（rad）；ωr—横摆角速度（rad/s）。

2.3 汽车二自由度模型

汽车操纵稳定性的基本特征可通过数学模型体现。建立一个线性二自由度汽车模型，如图2所示。在车辆的质心处分别沿横向和垂向建立转矩平衡方程，最终得到二自由度汽车数学模型，如式（9）、式（10）所示。直接将前轮转角θf作为输入，将横摆角速度wr、质心侧偏角β作为输出，横摆角速度与质心侧偏角又可以作为输入去计算转向阻力矩，如式（8）所示。

图2 二自由度汽车模型Fig.2 Two-Degree-of-Freedom Vehicle Model

式中：Kf、Kr—前后轮胎的侧偏刚度（N/rad）；a、b—前轴、后轴到整车质心的距离（m）；m—整车的质量（kg）；Jz—车辆绕z轴的转动惯量（kg·m2）。

3 EPS系统综合模型

3.1 补偿控制

汽车安装EPS系统后，增加了电机和减速机构，由此增加了系统中的阻尼和摩擦，而在设计EPS基本助力曲线中没有考虑这些因素，因此需对阻尼和摩擦进行补偿控制。经过电压补偿控制后的目标电压为：

式中：Kv—助力增益系数；Kj—阻尼补偿系数；Kd—摩擦补偿系数。

3.2 补偿控制EPS综合模型

根据前面的EPS系统模型、轮胎模型、二自由度整车模型和电压补偿控制可以建立电压补偿控制的EPS综合控制模型，其结构，如图3所示。

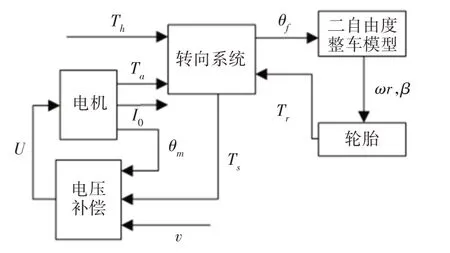
图3 电压补偿控制的EPS系统结构图Fig.3 EPS System Structure Diagram of Voltage Compensation Control

选取系统状态向量x=系统的输入向量u=［Th I0］T；系统输出向量y=［Ta Ts ωr］T。可将上述综合控制系统写成标准的状态空间形式：

4 基于电压补偿的H∞控制

电压补偿控制设计过程中，考虑了实际EPS系统中附加机械结构存在的阻尼和摩擦的影响，同时外界干扰影响EPS系统的转向性能。鲁棒控制优越的抗干扰性能，使得越来越多的学者将鲁棒控制运用到EPS系统中。为兼顾实际EPS系统的阻尼摩擦以及外界干扰对系统的影响，设计基于电压补偿的鲁棒H∞控制器。

4.1 混合灵敏度问题

鲁棒控制是为给定的系统找到一个控制器，使闭环系统具有鲁棒性。主要考虑的是传感器噪声和路面干扰这类加性干扰对系统的跟踪性能及抗干扰能力的影响［13］，因而可将此问题看成求解混合灵敏度问题，标准的混合灵敏度问题模型，如图4所示。

图4 混合灵敏度控制模型Fig.4 Mixed Sensitivity Control Model

式中：G—标称系统传递函数；K—H∞控制器的传递函数；r—参考输入；z1、z2、z3—控制系统的评价输出；e—跟踪信号误差；u—控制信号输入；y—系统输出；Ws、Wr、Wt—灵敏度加权函数、控制变量加权函数、补灵敏度加权函数；Gp—加入权函数的广义被控对象。H∞混合灵敏度问题就是求解一个合适的控制器K使得闭环系统内部稳定且满足［14］：

式中：ξ—一个很小的正数，默认为1。

4.2 H∞鲁棒控制器的设计

基础的电压补偿控制的鲁棒稳定性和跟踪性能较差，可在电压补偿控制的基础上，增加并联的H∞鲁棒控制，对EPS系统的中的干扰信号进行补偿。将上述的电压补偿EPS综合模型看作混合灵敏度控制模型中的标称系统G，引入加权函数后的广义被控对象为Gp，鲁棒控制输入电流Id。因此得到综合EPS鲁棒H∞控制模型，如图5所示。其中控制电流由两部分组成，一个为电压补偿控制产生的电流，一个为H∞鲁棒控制电流：I=Id+I0。

图5 综合EPS鲁棒H∞控制模型Fig.5 Comprehensive EPS Robust H∞Control Model

控制目标是保证良好的跟踪性能，转向路感以及操纵稳定性。所以定义控制系统的性能指标为：

Kp为常数，为了便于控制，将扭矩传感器的测量值表示驾驶员的感觉［13］。即上式可以表示为：

图6 Φ随车速变化曲线Fig.6 Φ Variation Curve with Vehicle Speed

图7 Kwr随车速变化曲线Fig.7 Kwr Variation Curve with Vehicle Speed

es表示实际传感器测量值与理想传感器测量值的差值。

根据国家标准GB/T 6323［15］，可知横摆角速度是评价汽车操纵稳定性的重要性能指标之一，理想横摆角速度即汽车转向进入稳定状态时的响应值。处于稳定状态时，汽车二自由度模型和EPS 转向模型各个变量的加速度为0，代入式（1）、式（6）、式（9）、式（10）可得期望横摆角速度与方向盘转角的比值Kwr。

ewr为实际横摆角速度与期望值横摆角速度之间的差值。

4.3 综合EPS鲁棒H∞控制器求解

将驾驶员操纵力矩Th、传感器噪声ds与路面干扰dr作为系统的参考输入，可以得到不含加权函数的广义系统状态空间模型［16］，如式（15）所示。

系统 状态 向量X=1考输 入w=［Th ds dr］T；开环系统输出y=［Ta Ts ωr］T；控制输入u=［Id］；系统评价输出z=［e u y］T；测量输出Y=［ea es eωr］T。

加权函数Ws、Wr、Wt的选取是求解鲁棒H∞控制器的难点，Ws应该具有高增益低通特性，Wr一般取一个较小的实数，Wt具有高通滤波特性［7］。经过反复验证可以得到Ws、Wr和Wt：

利用MATLAB软件求解H∞控制器，可以得到控制器：

其中AK为（13×13）维，BK为（13×3）维，CK为（13×1）维，DK等于0。求解得到ξ=0.7540＜1，满足系统鲁棒控制要求。

5 仿真结果

5.1 无干扰仿真分析

首先采用电压补偿控制，调节阻尼补偿系数和摩擦补偿系数使得EPS 系统响应曲线达到较为理想的状态，此时Kj=0.1、Kd=2.5。所得到的Kj、Kd代入到式（15）中，在MATLAB中通过M文件编写求解得到并联的H∞控制器K。在SIMULINK环境中搭建EPS仿真模型，将得到的H∞控制器K运用到EPS仿真模型中。假设车辆速度为25km/h，驾驶员在1s时产生1N·m的单位阶跃操纵力矩。分别采用电压补偿控制和基于电压补偿的鲁棒H∞控制，观察两种控制的仿真结果。主要考虑汽车转向中助力跟踪性能、转向路感以及操纵稳定性。根据前文可知，可以分别利用辅助扭矩、传感器测量值和横摆角速度来描述各性能的好坏。

两种控制方法下，辅助扭矩的对比图，如图8所示。与电压补偿控制对比，采用基于电压补偿的鲁棒H∞控制时，辅助扭矩能更好的消除振荡，达到稳定的时间从1.82s降低到1.37s，同时超调量降低了11.2%。总体来说，基于电压补偿的鲁棒H∞控制下的辅助扭矩响应更平滑，更快达到平衡，说明基于电压补偿的鲁棒H∞控制具有更好的助力跟踪性能。

图8 辅助扭矩响应对比图Fig.8 Comparison of Auxiliary Torque Response

扭矩传感器测量值对比图，如图9所示。

图9 扭矩传感器测量值响应对比图Fig.9 Comparison of Torque Sensor Measurement Values

电压补偿控制在阶跃输入后（1～2）s内产生了剧烈振荡，驾驶员能感受到方向盘的抖动，且超调量很大，调节时间较长，在2.2s才趋于稳定。而基于电压补偿的鲁棒H∞控制的最大超调量约为8%，远远小于电压补偿控制的最大超调量52%；且在1.3s左右就达到了稳定状态，调节时间大大缩短。显然基于电压补偿的鲁棒H∞控制可以使驾驶员获得更好的路感。

与理想横摆角速度进行对比可知，电压补偿控制的横摆角速度较低，达到稳态平衡的时间约为2.3s，最大超调量为17%，如图10所示。而加入鲁棒H∞控制后，横摆角速度更接近理想值，达到稳态的时间缩短至1.5s，最大超调量降低至2%，且达到峰值的时间也从1.4s缩短至1.3s。说明基于电压补偿的鲁棒H∞控制具有更优越的操纵稳定性。

图10 横摆角速度响应对比图Fig.10 Comparison of Yaw Rate Response

5.2 加入干扰仿真分析

在低速状态下，系统的抗干扰能力难以体现。设置汽车速度为80km/h，方向盘操纵力矩以1N·m的单位阶跃信号，在系统运行1s时输入，并加入高斯白噪声信号作为传感器噪声和路面干扰。电压补偿控制和基于电压补偿的鲁棒H∞控制的扭矩传感器测量值响应曲线图，如图11所示。通过比较可见，电压补偿控制持续受到干扰的影响，无法达到稳定状态。而基于电压补偿的鲁棒H∞控制能在2s的时间内达到稳定，稳定后的波动量较小，避免了方向盘“打手”现象，具有较强的抗干扰能力。

图11 加入干扰的扭矩传感器测量值对比图Fig.11 Comparison of Torque Sensor Measurement Values with Interference Added

实际横摆角速度与理想横摆角速度的差值ewr可以反应干扰对汽车的操纵稳定性的影响，ewr的值越小，说明实际横摆角速度越接近理想横摆角速度。可见，ewr的值在阶跃输入的时候会有短暂时间的波动，最大波动值约为-1.6×10-3，波动值较小，经过1s的时间可稳定在0.2×10-3左右，可忽略不计，如图12所示。说明在加入干扰后，基于电压补偿的鲁棒H∞控制可以使该车的操纵稳定性能达到理想状态。

图12 加入干扰后ewr的变化值Fig.12 Change Value of ewr with Interference Added

采用固定方向盘检验阻力矩阶跃输入对路感的影响，如图13所示。显示的是转矩传感器测量实际的值和理想路感等效到转矩传感器上的值之间的差值es。在受到干扰的情况下，es的值出现一个暂态过程，其峰值（即最大的路感偏差）在1.3s 为3.5×10-3，随后稳定在2.25×10-3，偏差值较小，可约等于0，对路感控制效果较为理想。可以使驾驶员获得良好的路感。

图13 加入干扰后es的变化值Fig.13 Change Value of es with Interference Added

为验证该方法的抗干扰效果，引入基于电压补偿的鲁棒H2控制策略。在两种控制策略下，输入单位阶跃信号的方向盘转矩并加入高斯白噪声。最后得到的转矩传感器值，如图14 所示。在（1～2）s内，基于电压补偿的鲁棒H2控制策略的跟随性能以及抗干扰性能都比不上基于电压补偿的鲁棒H∞控制。而在2s之后，后者的抗干扰能力比不上前者。由此可以考虑结合两种方法的优点，研究混合H∞/H2鲁棒控制策略在EPS上的应用。

图14 方法对比Fig.14 Method Comparison

因此，应用基于电压补偿的鲁棒H∞控制，EPS系统可以获得较好性能：（1）助力跟踪性能（波动小，稳定快）；（2）转向路感，无论是在有干扰还是无干扰情况下，驾驶员可以获得较为理想的路感，及时获取到路面信息；（3）操纵稳定性，横摆角速度更接近理想值，且超调量降低至2%；（4）抗干扰能力，在考虑转矩传感器和路面两种干扰的情况下，基于电压补偿的鲁棒H∞控制可以有效抑制干扰，快速达到稳定。

6 结论

（1）首先建立EPS数学模型，根据电压补偿控制机制建立电压补偿控制的EPS系统状态空间。（2）在电压补偿控制的基础上，以良好的跟踪性能，转向路感以及操纵稳定性为控制目标建立EPS 的混合灵敏度控制模型。（3）最后在MATLAB/SIMULINK 中搭建相应的动态模型，并进行仿真对比，结果表明基于电压补偿的鲁棒H∞控制能提升EPS系统的助力跟随性能，有效抑制外界干扰对EPS系统的影响，也进一步提高EPS的操纵稳定性。下一步工作将是对比H∞、H2、混合H∞/H2三种控制策略在跟随性能和鲁棒稳定性上的控制效果，并实现实车实验。