一类brace中的thin边

林梦丹, 卢福良

（闽南师范大学数学与统计学院, 福建 漳州 363000）

1 研究背景

只考虑有限简单图，除非另有说明，沿用文献[1]的标号.图的匹配是指图的边子集，其中任意两条边都不相邻.当匹配饱和图中所有的顶点，称为完美匹配.设图G为至少两个顶点的连通图，若其任意一边都属于某个完美匹配，称图G为匹配覆盖图.令X是V(G)的非空真子集=V(G) -X，G的边割是一个端点在X中，另一端点在中的所有边，记为∂(X).

在匹配覆盖图中，若边割C:=∂(X)，满足对任何完美匹配M，都有|M∩C| =1，称C为紧割.当X或-X只包含一个点时，边割C总是紧割，称这样的紧割为平凡的，其余的称为非平凡的.假设匹配覆盖图G中没有非平凡紧割，若G是二部图，称G为brace，反之称为brick.对二度点v的双收缩是指将点集{v,v1,v2}收缩为一个点，再去掉重边的操作，其中：v1和v2是点v的两个邻点.在图G中重复对二度点的双收缩得到的图，记为.若G中无二度点，G即为设图G是brace，若仍是brace，则e为图G的thin边.反之，e为图G的non-thin边.特别地，在brickG中，若G-e仍为匹配覆盖图，且最多有一个brick，称边e为图G的b-invariant边.若X和A为图G的点子集，记X∩A为XA.

Mccuaig[2]证明每个brace 都包含一条thin 边，进一步证明所有brace 都可以由三种brace 生成.Carvalho等[3]证明每个brace至少包含两条thin边.基于上述结果的启发，进一步研究了brace中的thin边，证明若C4为一个brace中的一个四圈，且该圈中包含两个相邻三度点的，则C4中至少包含一条thin边.

Carvalho等[3]提出了下列猜想.

猜想1每个顶点数至少为6的brace有两条不相邻的thin边.

猜想2存在正整数c，使得每个braceG有c|V(G)|条thin边.

类似地，在非二部图中也有考虑一类特殊thin 边—b-invariant 边.若2 边连通三正则图G没有非平凡的3-边割，称图G为基本4连通的.Kothari等[4]证明了除Peterson图外，每个基本4连通三正则non-near-bipartite brickG至少有|V(G)|条b-invariant边，并提出猜想：除外，每个4-边连通三正则near-bipartite brickG有条b-invariant边.Lu等[5]证明了上述猜想，并证明了该下界是可达的.

对上述两个猜想，到目前为止，还没有相关结果.主要原因在于在brace中没有较好的办法来找出thin边，特别在图的顶点数较多时（Carvalho 等[3]证明每个brace 至少存在两条thin 边，但没有给出如何找到这些thin边，即使是找到一条thin边）.在一类特殊的结构中，确定了brace中thin边在该结构的存在性.

2 预备知识

Hall证明了二部图中存在完美匹配的充要条件.

定理1[1]设G是具有二分类(A,B)的二部图，则G存在完美匹配当且仅当|A| =|B|，且|N(S)| ≥|S|，对于所有S⊆A成立.

关于brace有以下等价条件

定理2[6-7]设G是具有二分类(A,B)的匹配覆盖二部图，记为G(A,B)，下列条件等价：

1）G是brace；

2）任意a1,a2∈A，任意b1,b2∈B，G-a1-a2-b1-b2有完美匹配；

3）任意X⊆A，1 ≤|X| ≤|A| -2，有|N(X)| ≥|X| +2.

根据定理2有以下推论.

推论1若图G是顶点数至少为6的brace，有δ(G) ≥3.

推论2令G(A,B)是brace，X⊆V(G),|X∩B| ≤|B| -2，且N(XB) ⊆XA，

1）若|XA| =|XB|，则X=∅，

2）若|XA| =|XB| +1，则XB=∅.

设G(A,B)是匹配覆盖二部图，X是G的点子集，且|X|为奇数.显然，|XA|和|XB|不相等，不妨设|XA| ＞|XB|，记XA为X+，记XB为X-.

Lovasz[6]刻画了匹配覆盖二部图中的紧割.

定理2[6]设G(A,B)是匹配覆盖二部图，∂(X)是图G中的割，|X|为奇数，则∂(X)为紧割当且仅当

1）|X+| =|X-| +1，

2）∂(X)中每条边和X-中的点不关联.

推论6假设e是braceG中的non-thin 边，则存在X⊆V(G)(|X| ≥5,|| ≥5且为奇数)，使得∂(X)是G-e的非平凡紧割，且E[XA,B] ={e}，其中：E[XA,B]是一个端点在XA中，另一个端点在B中的所有边.

由推论3 可知，在braceG(A，B)中，对于每条non-thin 边e，都存在G中一个边割∂(X)，使得∂(X) -e是G-e的一个非平凡紧割，称这样的割∂(X)为关联边e的一个S-割.non-thin 边e的结构如图1 所示.涉及的所有图中，两个端点都在X的边不画出.注意，G中的一条non-thin边可能关联许多不同的S-割.

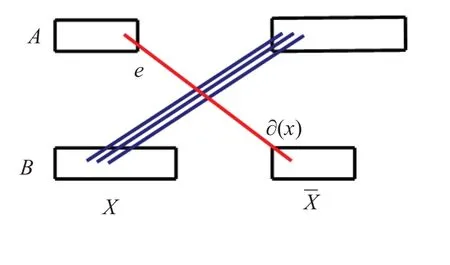
图1 e是non-thin边Fig.1 e is non-thin edge

3 主要结果及证明

定理3若C4=u1v1u2v2u1为braceG(A,B)中的一个四圈，且该圈中包含两个相邻三度点，则C4中至少包含一条thin边.

证明下面将采用反证法，利用推论3 中brace 含有non-thin 边的特殊结构导出矛盾，从而完成对定理的证明.

假设结论不成立.即u1v2,u2v2,u1v1,u2v1都为G中non-thin 边.不失一般性，设d(u1) =d(v2) =3，{u1,u2}⊆A，并设∂(X),∂(Y),∂(Z),∂(W)分别是关联u1v2,u2v2,u1v1,u2v1的S-割.

根据N(X2B) ⊆X2A∪{u2}和N(Y2B) ⊆Y2A∪{u1},有N(X2Y2B) ⊆X2Y2A.由定理1，有|N(X2Y2B)|≥|X2Y2B|，从而有|X2Y2A|≥|X2Y2B|.根据式（2）～（3），有|X1Y1A|≥|X1Y1B|.根据d(v2) =3,N(v2){u1}⊆X2A和N(v2){u2}⊆Y2A，有N(v2){u1,u2}⊆X2Y2A，从而有|X2Y2|≠0.根据N(X2Y2B) ⊆X2Y2A和推论4，有

如图2所示.

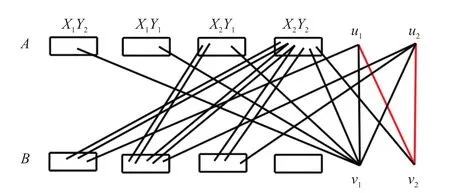
图2 u1v2,u2v2是non-thin边Fig.2 u1v2,u2v2are non-thin edges

假设|X2Y2A| ≥|X2Y2B| +3.根据式（2）～（3），有|X1Y1A| ≥|X1Y1B| +1.另一方面，根据N(X1Y1A) ⊆X1Y1B∪{v1}，有|N(X1Y1A)| ≤|X1Y1B| +1.根据|X1Y1A| +2 ≤|N(X1Y1A)|，可得|X1Y1A| ≤|X1Y1B| -1，矛盾.结合式（4）有以下两种情况.

情况1|X2Y2A| =|X2Y2B| +2.

根据式（1）～（3），有|X2Y1A| =|X2Y1B| -1，|X1Y1A| =|X1Y1B|和

其中：N(X1Y1A) ⊆X1Y1B∪{v1}.根据推论2，有|X1Y1| =0.根据N(Z2B) ⊆Z2A∪{u2}，有N(X2Y2Z2B) ⊆X2Y2Z2A.根据N(X2Y2Z2B) ⊆X2Y2Z2A和定理1，有

同理，有|X1Y2Z1A| ≤|X1Y2Z1B|和

根据d(u1) =3,N(u1){v1}⊆X1B,N(u1){v2}⊆Y2B,N(u1){v2}⊆Z1B，有N(u1){v1,v2}⊆X1Y2Z1B，即|X1Y2Z1| ≠0.根据N(X1Y2Z1A) ⊆X1Y2Z1B和推论2，可知|X1Y2Z1A| ≠|X1Y2Z1B|，进一步有

根据式（5）和式（8），有

同理，由式（6）可得到|X2Y2Z1A| ≤|X2Y2Z1B| +2和

如图3所示.

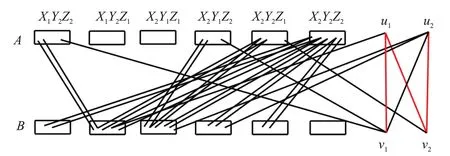
图3 u1v2,u2v2,u1v1是non-thin边且|X2Y2 A| =|X2Y2B| +2Fig.3 u1v2,u2v2,u1v1 are non-thin edges and |X2Y2 A| =|X2Y2B| +2

假设|X2Y2Z2A| ≥|X2Y2Z2B| +3.根据|Z2A| =|Z2B| +1 和式（10），有|X1Y2Z2A| ≤|X1Y2Z2B| -1，与式（9）矛盾.故结合式（6）有以下3种情况.

情况1.1|X2Y2Z2A| =|X2Y2Z2B|.

根据N(X2Y2Z2B) ⊆X2Y2Z2A，由推论4（1），有|X2Y2Z2| =0，从而可得|X2Y2Z1A| =|X2Y2Z1B| +2.假设|X2Y1Z1A| ≤|X2Y1Z1B| -3.根据|Z1A| =|Z1B| -1，得|X1Y2Z1A| ≥|X1Y2Z1B|，与式（8）矛盾.结合式（7）有以下3种情况.

如果|X2Y1Z1A| =|X2Y1Z1B| -2，根据|Z1A| =|Z1B| -1，有|X1Y2Z1A| =|X1Y2Z1B| -1，从而有|X1Y2Z2A| =|X1Y2Z2B|.根据N(X1Y2Z1A) ⊆X1Y2Z1B和N(X1Y2Z2B) ⊆X1Y2Z2A，由推论4 知，有|X1Y2Z2| =0和|X1Y2Z1A| =|X1Y2Z1B| -1，进一步有|X1| =1，与推论3矛盾.如果|X2Y1Z1A| =|X2Y1Z1B| -1，则|X2Y1Z2A| =|X2Y1Z2B|.根据N(X2Y1Z1A) ⊆X2Y1Z1B，由推论2 知，|X2Y1Z1|=|X2Y1Z1B|=1，存在|X2Y1Z2|=0，从而有|Y1|=1，与推论3 矛盾.如果|X2Y1Z1A| =|X2Y1Z1B|，可得|X2Y1Z1| =0 和|X2Y1Z2A| =|X2Y1Z2B| -1.由N(X2Y1Z2A) ⊆X2Y1Z2B∪{v1}知，|N(X2Y1Z2A)| ≤|X2Y1Z2B| +1，与定理2矛盾.

情况1.2|X2Y2Z2A| =|X2Y2Z2B| +1.

如果|X2Y1Z1A| ≤|X2Y1Z1B| -2，易得|X1Y2Z1A| ≥|X1Y2Z1B| +3，与式（8）矛盾；如果|X2Y1Z1A| =|X2Y1Z1B| -1，易得|Y1| =1，与推论3 矛盾；如果|X2Y1Z1A| =|X2Y1Z1B|，易得|X2Y1Z1A| ≤|X2Y1Z1B| +1，与定理2矛盾.

情况1.3|X2Y2Z2A| =|X2Y2Z2B| +2.

假设|X2Y1Z1A| ≤|X2Y1Z1B| -1.可以得到|X1Y2Z1A| ≥|X1Y2Z1B|，与式（8）矛盾，故|X2Y1Z1A| =|X2Y1Z1B|，从而有|X1Y2Z1A| =|X1Y2Z1B| -1.根据N(X1Y2Z1A) ⊆X1Y2Z1B，由推论2，有|X1Y2Z1| =|X1Y2Z1B| =1.同理，有|X2Y1Z1| =0.为书写方便，记K1=X1Y2Z2，K2=X1Y2Z1，K3=X2Y1Z2，K4=X2Y2Z1和K5=X2Y2Z2.

根据N(W1A) ⊆W1B∪{v2}，有N(K1W1A) ⊆K1W1B，进一步有

同理，有|K3W1A| ≤|K3W1B|和

根据N(u2){v1,v2}⊆K3W1B和推论2，有

根据N(u1){v1,v2}⊆K2B，有|K2| =|K2W2| =|K2W2B| =1.由|W1A| =|W1B| -1，式（11）～（13），有|K4W1A| ≥|K4W1B|.根据N(v2){u1,u2}⊆K4W1A，得到|K4W1A| ≥|K4W1B| +1.否则|K4W1A| =|K4W1B|，与定理2矛盾，如图4所示.

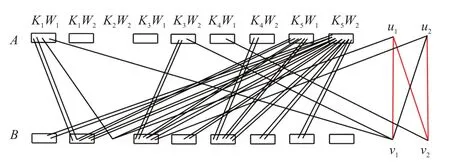
图4 u1v2,u2v2,u1v1,u2v1是non-thin边且|X2Y2Z2 A| =|X2Y2Z2B| +2Fig.4 u1v2,u2v2,u1v1,u2v1 are non-thin edges and |X2Y2Z2 A| =|X2Y2Z2B| +2

假设|K5W2A| ≥|K5W2B| +2.易证|K1W1A| ≥|K1W1B| +1，与式（11）矛盾.故结合式（12）有以下两种情况.

情况a|K5W2A| =|K5W2B|.

如果|K4W1A| ≥|K4W1B|，有|K1W1A| ≥|K1W1B| +1，与式（11）矛盾.

如果|K4W1A| =|K4W1B| +1.若|K3W1A| ≤|K3W1B| -3，可以得到|K1W1A| ≥|K1W1B| +1，与式（11）矛盾；若|K3W1A| =|K3W1B| -2，易证|K1| =|X1| =1，与推论6 矛盾；若|K3W1A| =|K3W1B| -1，易证|K3W1| =|K3W1B| =1，从而有|K3| =|Y1| =1，与推论6矛盾.

同理，如果|K4W1A| =|K4W1B| +2，和式（11）或推论6矛盾.

情况b|K5W2A| =|K5W2B| +1.

假设|K4W1A| ≥|K4W1B| +2.可得|K1W1A| ≥|K1W1B| +1，与式（11）矛盾.反之，|K4W1A| =|K4W1B| +1.若|K3W1A| ≤|K3W1B| -2，有|K1W1A| ≥|K1W1B| +1，与式（11）矛盾；若|K3W1A| =|K3W1B| -1，易证|K1| =|X1| =1，与推论3矛盾.

情况2|X2Y2A| =|X2Y2B| +1.

根据式（1）～（3），有|X2Y1A| =|X2Y1B| -1，|X1Y1A| =|X1Y1B| -1和

根据N(X2Y2B) ⊆X2Y2A，由推论2 知，|X2Y2| =|X2Y2A| =1.根据N(v2){u1,u2}⊆Z1A，有N(v2){u1,u2}⊆X2Y2Z1A，从而有|X2Y2| =|X2Y2Z1A| =1.根据N(X1Y2Z2B) ⊆X1Y2Z2A，由定理1，有

同理，有

根据式（14）～（15），有

同理，有

根据|Z2A| =|Z2B| +1，式（15）和式（18）有

如图5所示.

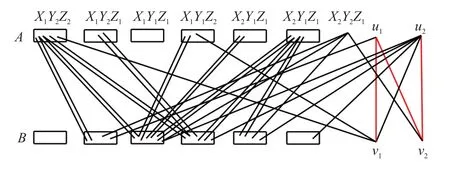
图5 u1v2,u2v2,u1v1是non-thin边且|X2Y2 A| =|X2Y2B| +1Fig.5 u1v2,u2v2,u1v1are non-thin edges and |X2Y2 A| =|X2Y2B| +1

假设|X2Y1Z2A| ≥|X2Y1Z2B| +2.根据|Z1A| =|Z1B| -1，有|X1Y2Z2A| ≤|X1Y2Z2B| -2，与式（15）矛盾.结合式（19）有以下两种情况.

情况2.1|X2Y1Z2A| =|X2Y1Z2B| +1.

如果|X1Y1Z1A| ≤|X1Y1Z1B| -2，易证|X1Y2Z1A| ≥|X1Y2Z1B| +1，与式（17）矛盾；如果|X1Y1Z1A| =|X1Y1Z1B| -1，有|X1Y1Z1| =|X1Y1Z1B| =1，从而有|N(X1Y2Z1A)| ≤|X1Y2Z1B| +1，与定理2 矛盾.故|X1Y1Z1A| =|X1Y1Z1B|，可以得到|X1Y1Z1| =0.

易证|X1Y2Z2W2| =|X1Y2Z2W2A| =1 和|X1Y2Z1W2| =|X1Y2Z1W2B| =1.令X1Y2Z1W2B={x}，根据N(X1Y2Z1W2B)⊆X1Y2Z2W2A∪{u1}，有d(x) ≤2，与推论3矛盾.

情况2.2|X2Y1Z2A| =|X2Y1Z2B|.

根据|N(X2Y1Z2B)| ≤|X2Y1Z2A| +1，由定理2 知，|X2Y1Z2| =0.如果|X1Y1Z1A| ≤|X1Y1Z1B| -3，由|Z1A| =|Z1B| -1，有|X1Y2Z1A| ≥|X1Y2Z1B| +1，与式（17）矛盾；如果|X1Y1Z1A| =|X1Y1Z1B| -1，易证|X1Y1Z1| =|X1Y1Z1B|=1,|X2Y1Z1A| =|X2Y1Z1B|.根据|N(X2Y1Z1A)| ≤|X2Y1Z1B| +1，由推论4（2）知，|X2Y1Z1| =|X2Y1| =|X2| =1，与推论3矛盾；如果|X1Y1Z1A| =|X1Y1Z1B|，易证|X2Y1Z1| =0，从而有|X2Y1| =|X2| =1，与推论3矛盾.

故|X1Y1Z1A| =|X1Y1Z1B| -2.由推论2，易证|X2Y1Z2| =0 和|X1Y2Z2| =0.为书写方便，记F1=X1Y2Z1，F1=X1Y2Z1,F2=X1Y1Z1,F3=X1Y1Z2,和F5=X2Y2Z1.容易得到|F3W2A| ≤|F3W2B| -1，

如图6所示.

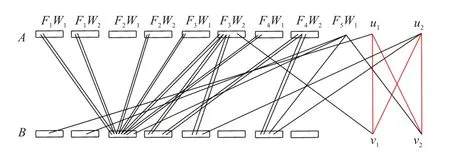
图6 u1v2,u2v2,u1v1,u2v1是non-thin边且|X2Y1Z2 A| =|X2Y1Z2B|Fig.6 u1v2,u2v2,u1v1,u2v1 are non-thin edges and |X2Y1Z2 A| =|X2Y1Z2B|

假设|F4W1A| ≤|F4W1B| -2.从而有|F1W1A| ≥|F1W1B| +1，与式（21）矛盾.故结合式（20）有以下两种情况.

情况a|F4W1A| =|F4W1B|.

易得|F4W2A| =|F4W2B|.根据N(F4W2B) ⊆F4W2A，由推论2 知，|F4W2| =0，存在|F4W1| =0，故|X2| =1，与推论3矛盾.

情况b|F4W1A| =|F4W1B| -1.

如果|F3W1A| =|F3W1B|，易证|F3W2| =|F3W2A| =1，存在|F3W1| =0，故|Z2| =1，与推论3矛盾.反之，|F3W1A| ≤|F3W1B| -1，根据|W1A| =|W1B| -1，有|F1W1A| ≥|F1W1B| +1，与式（21）矛盾.

所以，C4中至少包含一条thin边.

若C4中存在两个不相邻的三度点但无两个相邻的三度点，则定理7结论不成立.如图7所示，u1和u2为两个不相邻的三度点，且u1v2,u2v2,u1v1,u2v1是non-thin边.

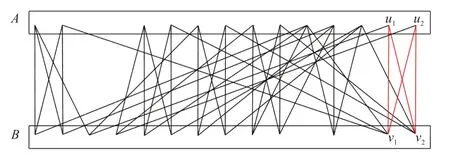
图7 一个例子Fig.7 An example