移动边缘网络中基于强化学习的部分卸载分析

王景弘, 陈 昱, 胡建强

（厦门理工学院计算机与信息工程学院,福建 厦门 361024）

随着移动边缘网络的普及，自动语音识别（automatic speech recognition, ASR）、自然语言处理（natural language processing, NLP）和计算机视觉（computer vision, CV）[1-3]等应用都需要计算资源来保证体验质量（quality of experience, QoE）和服务质量（quality of service, QoS）.由于智能移动设备的计算能力和电池电量有限，从用户到服务器的计算卸载成为移动边缘计算（mobile edge computing, MEC）优化资源利用率、能耗和网络延迟的重要支撑技术[4].

移动边缘计算MEC 环境中，由于用户设备存在各异的通信条件和计算要求，在满足最小时延要求下协调多个用户间的计算卸载较为困难.在移动边缘计算环境中，任务卸载通常被设置为二进制计算卸载[5]，即计算任务只能在用户设备（user equipment, UE）上本地计算，或完全卸载给MEC 服务器计算，任务卸载过于简单化而且决策的准确性不高.特别是，不同的用户设备通常处于移动状态，各用户之间的通信情况会时刻变化.采用强化学习（reinforcement learning, RL）[6]在移动边缘计算卸载有许多应用，但状态空间和动作空间的需求增强使得求取Q值困难[7].

假定在供能充足、不需过度考虑能耗条件的移动边缘网络环境下，优化卸载决策的延迟，从而降低总的服务延迟，提高用户的体验质量.为此，提出了一种基于强化学习的部分任务卸载方法，即采用Q-learning算法手动设置卸载率用于离散卸载决策，并使用深度确定性策略梯度算法DDPG-PO进行连续卸载决策，解决Q表的维数较大而导致搜索困难的问题.最后，采用实验验证上述方法的有效性.

1 相关工作

近年来有很多人工智能算法应用到移动边缘计算卸载领域.文献[8]提出了一种基于深度RL 的在线卸载（DROO）框架，DROO在网络上的输出使用S形激活函数来限制输出.当输出结果大于0.5时，任务将被完全卸载到MEC 服务器.否则，任务将在UE 上本地计算.文献[9]使用Q学习和深度Q网络（DQN）算法来寻找计算卸载策略.Q学习和DQN 算法比较了本地计算方案和计算卸载方案的长期回报大小，选择了与更大的长期回报相对应的计算卸载策略.文献[10]研究了雾计算中的迁移机制，并对容器迁移和虚拟机迁移两种方案进行了比较，得出了容器迁移比虚拟机迁移方案更轻量级的结论.其在计算卸载策略中使用了深度Q学习方法，以减少计算任务的延迟和能耗，以及容器迁移的成本.文献[11]研究了物联网场景中的计算卸载策略，并使用DQN 学习计算卸载策略.其中动作空间是离散物联网设备的传输功率，如果传输功率为零，则表示本地计算.然而，离散传输功率存在动作空间过大的问题.文献[12]研究了物联网场景下边缘计算的带宽资源分配问题，并使用DQN 学习带宽资源分配策略，以优化物联网设备的服务延迟和能耗.但由于离散域中的带宽资源分配不均，也存在带宽资源利用率不足的问题.

根据上述研究，启发式算法和RL算法是解决计算卸载时延优化问题的常用方法.但启发式算法很容易陷入局部最优解，算法的性能与具体问题和设计者的经验密切相关.深度强化学习结合了深度学习和RL 的优势，从高维原始数据学习控制策略，扩充系统的状态空间和可能发生的动作空间，并获得长期的回报，加强决策的准确性和时效性.

2 系统模型与问题建模

从网络模型、计算任务模型、本地计算模型和部分卸载边缘计算模型等方面介绍系统模型，并提出了问题框架.表1列出了主要符号.

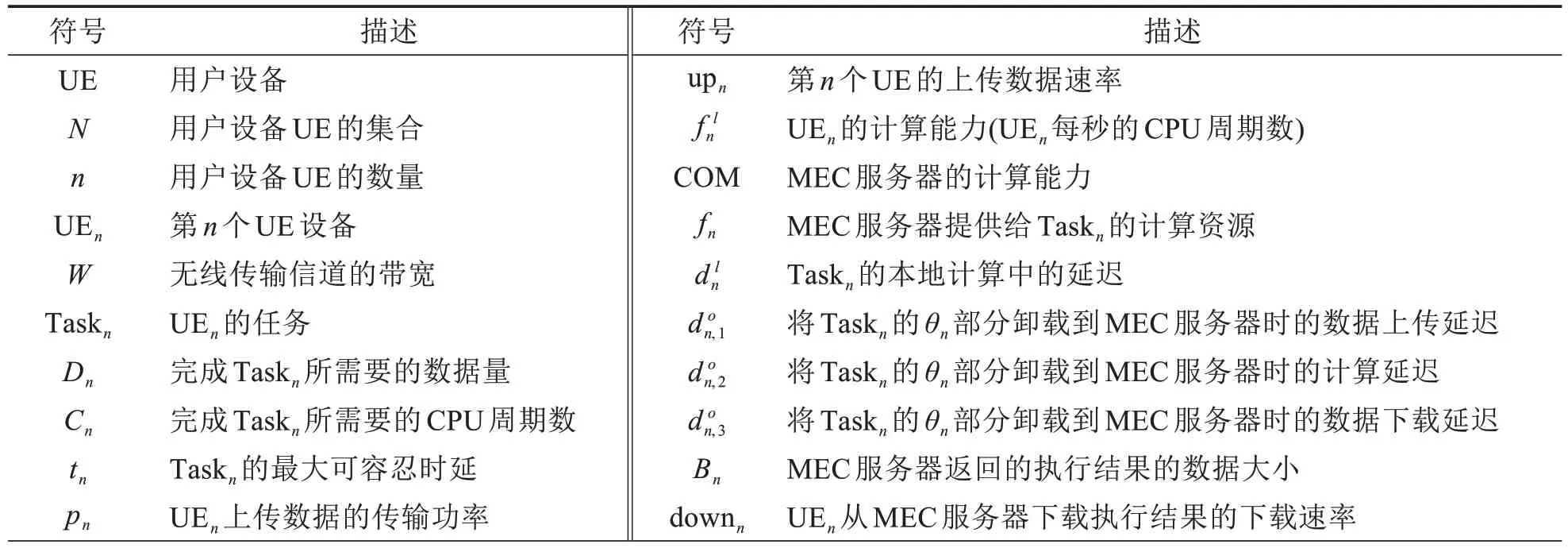
表1 主要符号Tab.1 Main symbols

2.1 网络模型

MEC系统含有n个UE 和1 个与基站部署在一起的服务器，UE 的集合表示为N= {1，2，…，n}. UE 可以把任务卸载给边缘服务器，利用服务器的高算力来减少计算延迟. 根据参考文献[9]的描述, 假设每个UE的任务优先级是相同的，每个UE可以获得相同的传输带宽资源，UEn的传输速率为

其中：W是无线信道的带宽；K是正在计算卸载的UE 的数量；pn是UEn的上传数据的传输功率；hn是UEn和基站之间的无线信道增益；G0是高斯白噪声的方差[9].

2.2 计算任务模型

定义Taskn≜(Dn，Cn，tn)作为UEn需要执行的任务.该任务可以在本地计算，也可以通过计算卸载在MEC 服务器上计算[13].Dn表示完成此任务所需的数据量，包括需要处理的相关数据.Cn表示完成任务Taskn所需的CPU 周期的数量.通常Dn和Cn的大小是正相关的，并且Cn的大小不会由于计算卸载而改变.tn是任务Taskn的最大可容忍延迟，表示完成任务Taskn所需的时间不应大于tn.

定义λn∈[0，1]作为UEn的卸载策略，UEn将λn的部分卸载到服务器计算，而(1-λn)的部分是由UE本地计算的.UE集合N的整体卸载策略A表示为A=[λ1，λ2，…，λn].当λi=0时，表明Taski由UE本地计算；当λi=1 时，表明Taski被UE 完全卸载给服务器计算；当0 ＜λi＜1 时，表明Taski的λi部分卸载给服务器计算，(1-λi)部分由UE计算.

2.3 本地计算模型

当UE 在本地执行任务时，任务完成过程完全使用本地计算资源与MEC 服务器无关.定义dln来表示任务Taskn的本地计算中的延迟.dln的计算方法为

其中：fln表示UEn的计算能力（UEn每秒的CPU周期数）.

2.4 部分卸载边缘计算模型

当UE 请求计算卸载时，任务Taskn的λn部分被卸载到MEC 服务器，(1-λn)部分则是本地计算的.Taskn的λn部分的总延迟包括数据上传延迟、MEC计算延迟和数据下载延迟；(1-λn)部分的延迟类似于上一小节中介绍的本地计算延迟.

其中：fn是MEC服务器分配给Taskn的计算资源.定义COM 为MEC服务器的计算能力（MEC服务器每秒的CPU 周期数）.MEC 服务器分配给所有卸载任务的计算资源不应超过总计算资源，这表明应满足条件

其中：Bn是MEC 服务器返回的执行结果的数据大小；downn是UEn从MEC 服务器下载执行结果的下载速率.根据文献[14]，上传数据Dn的大小远大于返回数据的大小Bn，下载速率远大于上传速率，因此可以忽略数据下载延迟的影响.

由于Taskn的(1-λn)部分是UE计算的，所以它的计算延迟类似于上一节中的本地延迟.定义来表示Taskn的(1-λn)部分的计算延迟，计算方法为

基于上述公式（3）～（6），定义don为执行部分卸载策略时任务Taskn的总时延.由于各个Taskn之间并行执行，UEn进行部分卸载时的总时延应该是部分卸载时延和本地计算时延中更大的那一个.don的计算方法为

2.5 问题定义

公式（7）中，当λn=0 时可以得到don==dln；当λn=1 时可以得到=0.因此可以使用公式（7）来综合考虑本地计算、部分卸载和完全卸载三种策略的时间延迟.以最小化整个MEC 系统中所有UE 的任务执行时间作为优化目标，结合上述网络模型、计算任务模型、局部计算模型和边缘计算模型，优化目标和约束条件定义为

在优化问题（8）中，如果λn的值只能是0或1，搜索最优解的时间复杂度将随着UE数量的增加而呈指数级增加.文献[9]证明这类问题是一个NP-hard 问题.为了解决这个NP-hard 问题，引入了一种基于DRL的部分卸载方案，把λn的值从离散域变为连续域，有效地减少了MEC 系统的总时延.约束（9）表示每个Taskn既可以本地计算，也可以完全卸载到MEC 服务器，还可以进行任意比例卸载；约束（10）表示各个任务被服务器分配到的算力之和不能超过服务器总算力；约束（11）表示对于被卸载的任务都必须被分配到算力资源；约束（12）表示每个任务的完成时间don不应超过最大可容忍时延tn，否则会影响用户的体验质量.

3 基于Q-learning和DDPG的卸载算法

多用户多任务MEC 系统中结合边缘服务器资源分配、部分任务卸载和缓存决策的问题进行建模,目标是最小化整个MEC 系统中所有UE 的任务执行时间.为求解这个混合整数非线性规划问题，引入Qlearning算法并提出基于DDPG的优化算法DDPG-PO,尽可能地优化QoS并减小系统总时延.

3.1 深度强化学习框架

1）状态空间.为了将DRL 解决方案应用于系统模型和问题框架，需要定义状态空间、行动空间和奖励函数.理论上需要观察整个MEC系统来确定状态空间，包括用户数量、任务情况、计算资源的使用情况等.但事实上，完成这件事会造成额外的系统开销.随着MEC 服务器中UE 数量的增加，额外的系统开销将更大.考虑到优化目标是MEC 系统的总时延，所以将状态定义为，作为整个MEC 系统的时延.

2）动作空间.为了描述每个UE的计算卸载策略，将动作空间定义为MEC系统中所有UE的动作空间之和.对于每个UEn，定义它的动作空间为A=[λ1，λ2，…，λn]满足λi∈[0，1]，这意味着卸载方案不必局限于传统的二元卸载，进而扩展了传统DRL 的动作空间，并在更大程度上带来了优化MEC 系统总延迟的可能性.

3） 奖励函数.定义R(S，A)为奖励函数，表示代理在状态S下执行计算卸载策略A时获得的奖励.为了评估卸载策略的优缺点，奖励函数应该与所有UE 的总时延成反比.因此定义奖励函数为R(S，A) =，这表明卸载策略越好，系统时延越低，回报也就越大.

3.2 算法设计

1）Q-Learning 算法：Q-Learning 算法是一种传统且广泛使用的RL 算法，它包含与状态和动作对相对应的Q函数.Q函数表示在状态S和动作A下可获得的长期奖励的估计，用来选择具有最长奖励的最佳策略.Q函数的计算方法为

其中：s′是在状态s下采取行动a时达到的状态；α 是学习率；γ 是未来奖励的折现系数，0 ≤γ≤1，用来表示未来奖励的重要性.

根据以上对Q-learning算法的描述，还需要对状态空间和动作空间进行微调后才能应用该算法.对于状态空间，将状态四舍五入为一个整数；对于动作空间，则预定义了X+1个离散部分的计算卸载比率.定义UEn的卸载策略为，其中X的大小可以调整，X越大卸载策略越好，但与之对应的是更高的复杂度.每个UE 都有各自的动作空间，所以需要在Q函数中添加一个用户维度，用Q(S，N，X+1)表示.改进后的Q函数为

在公式（14）中，Q(s，i，λi)表示当MEC 系统处于状态s时，第i个UEi采用计算卸载策略λi时可以获得的长期奖励的估计.由于Q-table要求其索引为非负整数，因此在Q函数中的λi需要乘以X.公式（14）中的s'表示MEC系统中的所有UE采用卸载策略A之后的状态，其中A包含此时第i个UE的计算卸载策略.简而言之，MEC系统中所有UE都具有相同的状态s'.算法1展示了改进后的Q-learning算法.

算法1 预定义离散卸载率的Q学习算法1:初始化Q函数 Q(S，N，X+1);2:for occasion=1 do 3: 用随机计算卸载策略初始化状态s;4: repeat 5: 基于贪心策略从 Q-table 中选择执行动作 A=[λ1，λ2，…，λn];6: 执行动作 A;7: 得到奖励 r 和下一个状态 s';8: for i=1,N do 9: 用公式(14)更新 Q(s，i，λi X);10: end for 11: s ←s′12: until 达到期望状态 sterminal 13: end for

2）DDPG-PO 算法.在上一节中使用Q-Learning 算法通过手动设置X+1 部分的卸载率来实现部分卸载，但因为使用的是Q-table来储存所有Q值，随着UE数量的和预定义卸载率的增加，找全整个Q-table的难度也越来越大.所以引入DDPG-PO算法来解决这个问题.DDPG-PO算法包括actor网络和critic网络两部分.actor网络负责根据观察到的状态信息生成策略，而critic网络负责收集奖励值以评估和纠正策略.

DDPG-PO 算法将动作空间扩展到一个连续域，并使用一个特殊的重放缓冲器，该容器存储一定数量的记录，而不是传统RL算法中的Q-table.每个记录由[st，at，rt，st+1]组成，并使用该记录中的一个小批元组更新参数.

DDPG-PO 算法包含四个DNN.它们分别是actor 网络μ(s|λμ)，其网络参数用λμ表示；critic 网络Q(s，a|λQ)，其网络参数用λQ表示；目标actor 网络μ'(s|λμ')，其网络参数用λμ'表示；以及目标critic 网络Q'(s，a|λQ')，其网络参数由λQ'表示.actor网络负责根据状态选择要进行计算卸载的动作.目标critic网络和目标actor网络使用重放缓冲器来评估目标Q值，而critic网络负责计算Q值.目标Q值的计算方法为

对于critic网络的参数更新，使用梯度下降法来最小化目标Q值和critic网络输出之间的差异.损失函数是一个平方损失函数，其计算方法为

其中：N是批次号大小.使用Adam优化器[15]来最小化损失函数.actor网络使用梯度上升法更新策略，策略梯度为

对于目标网络参数更新，DDPG-PO 算法使用actor网络和critic网络的参数对目标网络执行软目标更新.软目标更新的方式为

其中：TOU 是目标网络的软更新因子.参数TOU 满足0 ＜TOU ＜1.TOU 越小，表明目标网络参数更新越慢.算法2展示了MEC系统的DDPG-PO算法的过程.

算法2 DDPG-PO (partial-offloading) 算法1: 将actor网络和critic网络的参数分别随机初始化为λμ和λQ;2: 设置λμ′←λμ;3: 设置λQ′←λQ;4: 初始化重放缓冲器R;5: for occasion=1 do 6: 随机初始化动作A以获得相对应的状态s1;7: for t=1, T do 8: 根据actor网络和附加噪声,选择相应的计算卸载策略 At=μ(st|λμ) +Nt, 其中 Nt 是正态分布的噪声扰动;9: 执行计算卸载策略At,得到奖励rt和下一个状态st+1;10: 将记录(st，at，rt，st+1)存储在重放缓冲区R中;11: 从重放缓冲区R中随机抽取记录;12: 用公式(15)计算目标Q值;13: 通过最小化损失函数公式(16)来更新critic网络的参数;14: 使用基于公式(17)的采样的策略梯度来更新actor策略;15: 基于公式(18)和(19)对目标网络的参数进行软更新;16: end for 17: end for

在DDPG-PO 算法的神经网络设计中，把actor 网络的输入层的维度设为1，用于MEC 系统的状态输入；把actor网络的输出层的维度设为N，表示所有UE的卸载策略.因为actor网络需要根据卸载策略进行动作，所以引入Sigmoid激活函数来缩放其输出.Sigmoid激活函数为

critic 网络的输入层由两个部分组成，一个是系统状态S，另一个是每个UE 的卸载策略向量；输出层的维度设为1，表示Q 值的预测.另外使用全连接层分别组成actor 网络和critic 网络的隐藏层.目标actor网络的结构与actor 网络的网络结构相同，目标critic 网络也与critic 网络结构相同.图1 展示了基于DDPG-PO的卸载架构.

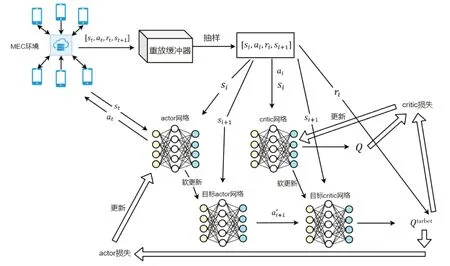
图1 基于DDPG-PO的卸载架构Fig.1 Offloading architecture based on DDPG-PO

4 实验评估

为了验证所提出卸载策略的优势，将其与文献[8]中的本地UE 计算（local computing）方案、完全卸载（full offloading）方案和DQN卸载策略进行了比较.

在实验设置中，用户数量可变并且均匀分布在距离服务器200 m的范围内.UE和MEC服务器之间的信道增益与距离成反比.无线信道增益设置为hn=dis-ns，其中s=3，disn是UEn和基站之间的距离.无线信道的带宽设置为W=10 MHz，背景噪声G0=-174 dBm/Hz，UE 上传功率pn=500 mW[16].MEC 服务器的计算能力设置为COM=5 GHz/s，并根据λnCn的大小均匀分布给每个任务.每个UE 的计算能力被设置为=1 GHz/s.UE 上的任务量Dn均匀分布为（300 Kbits，500 Kbits），Cn均匀分布为（900 兆周期，1 100 兆周期）[9].最大可容忍延迟设置为tn=dnl，表明如果计算卸载不能有效减少任务时延，则不需要把任务卸载给MEC 服务器，否则会带来额外负担.预定义的离散部分计算卸载率X=3，学习率α=0.1，折现系数γ=0.8.DDPG-PO算法中的相关参数如表2所示.

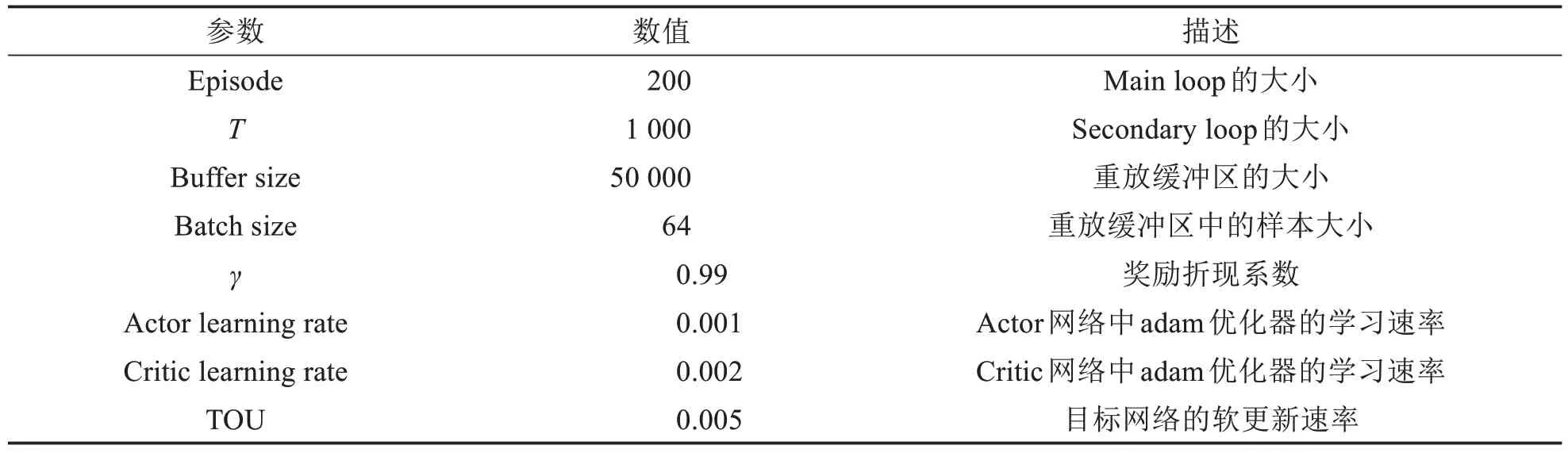
表2 DDPG-PO算法中的参数设置Tab.2 Parameter settings in DDPG-PO algorithm

图2展示了UE数量对系统总时延的影响.横坐标表示UE的数量，纵坐标表示所有UE的任务完成时间之和.MEC 服务器的计算能力为COM=5 GHz/s.在通常情况下，所有方案的总延迟都随着UE 数量的增加而增加.可以发现用户数量超过5时，完全卸载方案的总时延是最高的.这是因为此方案中所有任务都被卸载给MEC服务器，且由于计算能力有限，无法满足所有UE的计算需求.此时只有提高服务器的算力才能降低整体的时延.由实验结果可知这两种算法与其他策略相比更好地减少了时延.

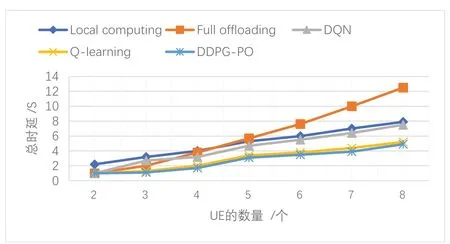
图2 不同UE数量下的总时延Fig.2 Total delay under different UE numbers

图3展示了MEC服务器的计算能力对系统总时延的影响.横坐标是MEC服务器的计算能力，纵坐标是所有UE的任务完成时间之和.UE的数量为N=5.由于本地计算不需要服务器参与，因此其结果是在图上是一条直线.通常随着MEC服务器计算能力的提高，系统总时延会减少，提高MEC服务器的计算能力有助于提高系统性能.随着边缘服务器计算能力提高，DQN接近完全卸载.Q-learning算法和DDPG-PO算法的时延总是低于DQN，这是因为Q-learning算法和DDPG-PO算法包含本地资源，但它们之间的差距逐渐减小.当COM ≥7 GHz/s时，系统的总延迟缓慢下降，这是因为此时限制系统总延迟的主要因素是传输时延.

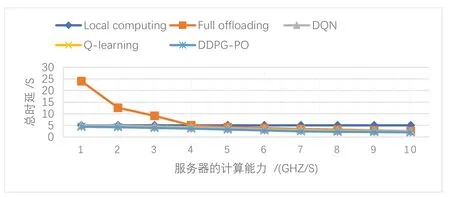
图3 MEC服务器的计算能力对系统总时延的影响Fig.3 The impact of MEC server's computing power on the total delay

当卸载策略A是二进制，即采用本地计算或者完全卸载时，在UE 数量少的情况下，可以通过列举在可接受的搜索时间内所有UE 的决策情况来找到最佳的卸载策略A′，从而获得二进制计算卸载的最小时延.归一化时延定义为

其中：D*(A)表示采用计算卸载策略A的时延.

为了验证所提出算法的优势，对比对象采用了文献[8]中提出的DROO策略.图4展示了不同UE数量下三种算法的归一化时延，横坐标是UE 的数量，纵坐标是归一化时延，MEC 服务器的计算能力设置为COM=5 GHz/s.对比了DROO算法之后可以发现，这是一种只支持本地计算或者完全卸载的二元卸载算法.DROO 算法的归一化时延均为1，这说明它可以得出在本地计算或者完全卸载中的最佳卸载策略.但本文提出的部分卸载策略的归一化时延均低于1，这说明部分卸载策略的时延要低于本地计算或者完全卸载.平均下来，Q-learning算法和DDPG-PO算法分别比DROO算法的时延低了21%和28%.由此也可以看出部分卸载相对于二元卸载而言，可以更好地减少系统总时延，提升用户体验质量.

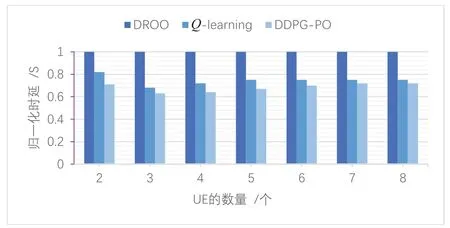
图4 Q-learning算法和DDPG-PO算法的归一化时延Fig.4 Normalized delay of Q-learning algorithm and DDPG-PO algorithm

图5展示了不同CPU周期对系统总时延的影响.横坐标是完成Taskn所需的CPU周期数，纵坐标是所有UE的任务完成时间之和.UE的数量为N=5，MEC服务器的计算能力为COM=5 GHz/s.横坐标的增加表明任务需要更多的计算资源.通常随着每个任务所需CPU 周期的增加，所有卸载方案的总时延都会增加.从实验结果可以发现，完全卸载的时延最高，本地计算次之，DQN 算法的时延相比它们而言低了很多，而这两种算法的时延最低，表现优于其他几种卸载策略.实验结果也从另一方面印证了所提出的卸载方案可以适应高计算量任务.

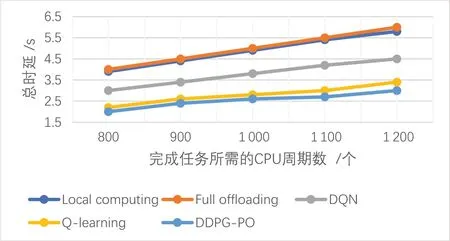
图5 不同CPU周期下的总时延Fig.5 Total delay under different CPU cycles

图6展示了两种算法的收敛性.横坐标是主循环的迭代次数，纵坐标为偶发性奖励，表示MEC系统在一个偶发情况中获得的总奖励.UE 的数量N=5，MEC 服务器的计算能力为COM=5 GHz/s.由奖励函数，偶发性奖励越大，系统总时延越低.根据实验结果可知，两种卸载策略随着迭代次数的增加，MEC 系统所获得的偶发性奖励也随之增加，这证明了所提出的两种策略在减少时延方面是有效的.在算法收敛速度方面，基于Q-learning 的离散计算卸载策略比基于DDPG-PO 算法的连续计算卸载策略收敛更快.在迭代了60次之后，Q-learning算法已经达到稳定状态.其收敛速度与X的值有关，通常X值越大收敛越慢.相比于Q-learning算法，DDPG-PO算法收敛得更慢但具有更强的降低总时延的能力.

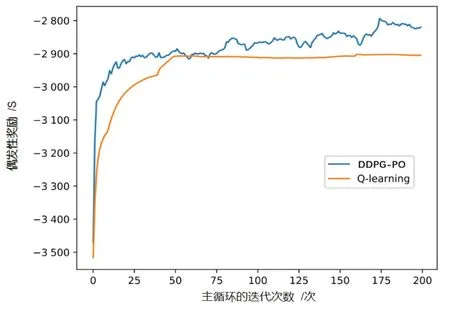
图6 Q-learning算法和DDPG-PO算法的收敛性Fig.6 Convergence of Q-learning algorithm and DDPG-PO algorithm

5 结语

研究物联网中多用户MEC 系统的部分计算任务卸载问题，优化的目标是尽最大可能减少MEC 系统的总时延.建立了一个适用于部分计算卸载的深度RL 模型，并提出了Q-learning 算法和DDPG-PO 算法的结合作为部分计算卸载策略，将二进制计算卸载方案扩展到连续动作域.仿真结果表明，与传统的本地计算和边缘计算相比，Q-learning算法和DDPG-PO算法可以有效地降低MEC系统的总时延.与最佳二进制计算卸载策略相比，Q-learning算法和DDPG-PO算法还将系统时延分别降低了21%和28%.