负必然-可能半三支概念及其应用

王启君, 林艺东*, 林宇静, 林梦雷,2

（1.闽南师范大学数学与统计学院,福建 漳州 363000；2.闽南师范大学数字福建气象大数据研究所,福建 漳州 363000）

形式概念分析（formal concept analysis，FCA）作为一种从形式背景进行数据分析和规则提取的强有力工具，由德国数学家Wille[1-2]于1982年提出.形式概念分析通过对本体的概念、属性、关系等用形式化的语境表述出来，生成形为（外延、内涵）二元对的形式概念，并利用伽罗瓦连接构造出概念格（Concept lattice）.目前FCA 的主要研究方向有属性约简、规则提取、三支概念分析和网络形式背景等[3-12].同时该理论已成功应用于博客数据分析、智慧城市等领域[13-16].

三支概念分析(three-way concept analysis,3WCA)是将三支决策理论[17]与FCA 相结合产生的一种知识发现理论[8-10].受三个论域范畴的启发，它基于对概念的二元理解，把FCA 扩展到三元情况[18]，因此很多FCA中的研究内容可平移到3WCA中，如：三支概念格构建和约简[19-24]、三支概念学习[25-27]以及模糊三支概念分析[26,28]等.同时3WCA也在冲突分析、医疗诊断等方面得到成功应用[29-31].

三支概念从共性角度对对象和属性进行三分，由于在某些实际情况中共性信息可能不那么重要，魏玲等[32]结合必然算子与可能算子提出必然-可能半三支概念，将单向对应思想引入3WCA，可以应用于团队合作问题，拓宽概念的语义.然而在教育教学中，老师不仅关心怎样能让小组合作达到最佳效果，还需要关注学生不会解决的问题便于教师及时采取措施以改善学生的学习状态，这就使得考虑负背景下的信息成为必要.基于此问题，提出负必然、负可能算子，并结合区间集[33]，定义负必然-可能半三支概念，进而生成负必然-可能半三支概念格，最后用教育教学中的实例说明该理论的实用性.

1 基础知识

本节给出三支概念分析的一些基础知识.

对于任意非空论域U，若P(U)为其幂集，令DP(U)=P(U)×P(U).

U上的区间集为

记U上所有的区间集记为IP(U).

定义1[2]设三元组(G,M,I)为一个形式背景，其中：G={g1,g2,…，gp}为对象集；M={m1,m2,…,mq}为属性集.I⊆G×M，若(g,m)∈I，则称对象g具有属性m.

对于任意X⊆G和A⊆M，定义算子*与算子为

其中：Ic=G×M-I.

特别地，对于任意的g∈G,m∈M，记{g}*为g*，{m}*为m*.

一些学者从模态逻辑的角度，将*算子称为充分算子，并陆续提出必然算子、可能算子以及对偶充分算子等概念[34-35].

给定形式背景(G,M,I)，对于任意X⊆G，A⊆M，必然算子□定义为

可能算子⋄定义为

定义2[32]设(G,M,I)为一个形式背景，对于任意X∈P(G)，定义对象导出必然-可能三支算子◁：，X◁=[X□,X⋄]，简称ONPE-算子.

定义3[32]设(G,M,I)为一个形式背景，对于任意若则称为对象导出必然-可能半三支概念，简称为ONPSE-概念，

其中X称为ONPSE-概念的外延，称为ONPSE-概念的内涵.

定义4[32]设(G,M,I)为一个形式背景，对于任意A∈P(M)，定义属性导出必然-可能三支算子▷：P(M)→IP(G)，A▷=[A□,A⋄]，简称ANPE-算子.

定义5[32]设(G,M,I)为一个形式背景，对于任意若，则称为属性导出必然-可能半三支概念，简称为ANPE-概念，

2 基于负信息的对象导出必然-可能半三支概念

上述提出的必然-可能半三支概念是基于正背景的角度，关注的是怎样合作使得团队更高效高质量地完成工作，而在教育教学中教师不仅需要关注学生已经掌握的知识点，也需关注学生不会解决的问题.这就需要利用负信息从另一方面对对象集、属性集的信息进行刻画.

2.1 对象导出负必然-可能三支算子

定义6给定形式背景(G,M,I)，对于任意X⊆G,A⊆M，负必然算子定义为

性质1设(G,M,I)为一个形式背景，对于任意X,X1,X2∈G,A,A1,A2∈M,有

证明(i)对∀a∈，有⊆X，即∩X=≠∅，则a∈，故X¯⊆.同理可证A¯⊆.

(ii)对∀a∈，有⊆X1，又X1⊆X2，有a-*⊆X2，则a∈，所以⊆.故当X1⊆X2时⊆.同理可证A1⊆A2⇒⊆.(iii)对∀a∈，有∩X1≠∅，又X1⊆X2，有∩X2≠∅，则a∈，所以⊆.故当X1⊆X2时有⊆.同理可证A1⊆A2⇒⊆.

例1表1为形式背景(G,M,I)，其中对象集G={1,2,3,4}代表四名学生，属性集M={a,b,c,d}代表学生在学习过程中需要解决的问题.表1 中“1”表示学生会解决此问题，“0”则表示学生不会解决此问题，如：学生1会解决的问题有a,c,d,不会解决的问题为b.

表1 形式背景(G,M,I)Tab.1 Formal context (G,M,I)

定义7设(G,M,I)为一个形式背景，对于任意X∈P(G)，定义对象导出负必然-可能三支算子：P(G)→IP(M)，，简称NONPE-算子.

NONPE-算子具有以下性质：

性质2设(G,M,I)为一个形式背景，对于任意X1,X2∈P(G)，有

证明(i)若X1⊆X2，由性质1(ii) ～(iii)，有，则

2.2 对象导出负必然-可能半三支概念

定义8设(G,M,I)为一个形式背景，对于任意X∈P(G)，，若，则称为对象导出负必然-可能半三支概念，简称为NONPSE-概念，其中X为NONPSE-概念的外延，为NONPSE-概念的内涵.

对于对象子集X⊆G，NONPE-算子可以同时获取必然属性与可能属性，并形成属性集M上的一个区间集，这个区间集可将M分为3 部分：正域POSX=、负域NEGX=M-以及边界域并且POSX、NEGX和BNDX两两互不相交，形成M的一个弱三划分.

例2表1形式背景下所有的概念如表2所示.

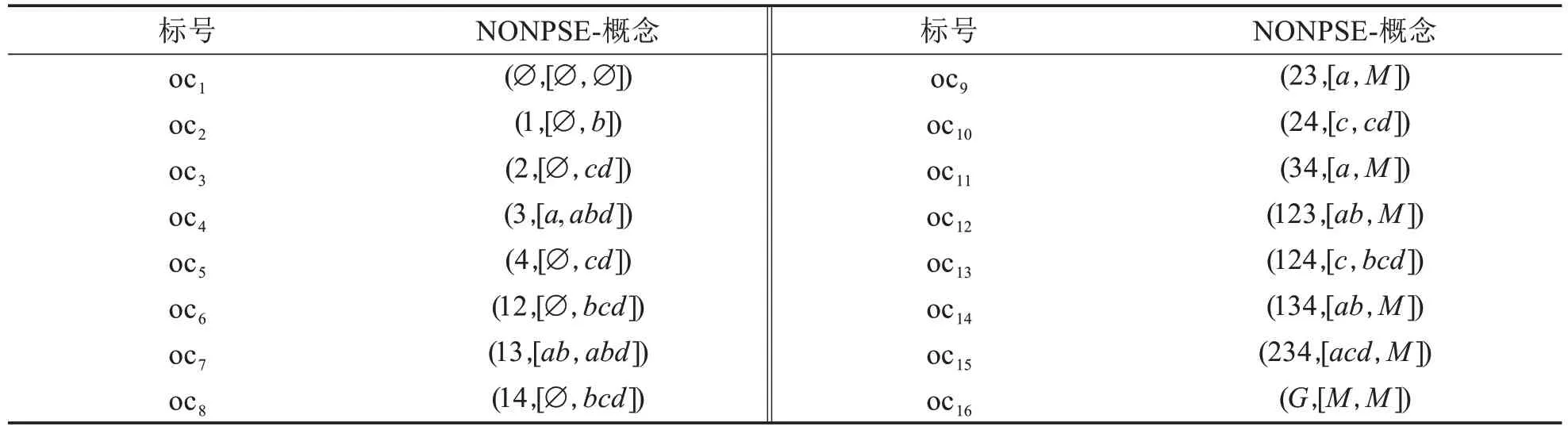
表2 表1 的NONPSE-概念Tab.2 NONPSE-concept of Table1

以概念(23,[a,M])， (34,[a,M])为例解释NONPSE-概念的语义.概念(23,[a,M])表明：不会解决问题a的学生一定在2 和3 中，且学生2 和3 不会解决的问题在M中；概念(34,[a,M])表明：不会解决问题a的学生一定在3和4中，且学生3和4不会解决的问题在M中，进一步可以说明，学生3一定不会解决问题a，也符合概念(3,[a,abd])的语义.

记(G,M,I)的所有NONPSE-概念的集合为NONPSEL(G,M,I)，定义其偏序关系为：对于任意

称NONPSEL(G,M,I)为(G,M,I)的对象导出负必然-可能半三支概念格，简称为NONPSE-概念格.定理1给出其上、下确界，并证明其是一个完备格.

定理1NONPSEL(G,M,I)是一个完备格，其上、下确界分别为

证明对于任意的由NONPE-算子的定义可知

则X1⊆X且X2⊆X，故X1∪X2⊆X，因此

定理2ONPSEL(G,M,I)≅NONPSEL(G,M,I).

证明记 ONPSEL(G,M,I)=L(G,M1,I1)，NONPSEL(G,M,I)=L(G,M2,I2)，对任意，总存在使得X′=X，则L(G,M1,I1)≤L(G,M2,I2)；又对任意总存在使得X=X′,则L(G,M2,I2)≤L(G,M1,I1)，故L(G,M1,I1)≅L(G,M2,I2)，即ONPSEL(G,M,I)≅NONPSEL(G,M,I).

例3表1的NONPSE-概念格如图1所示.

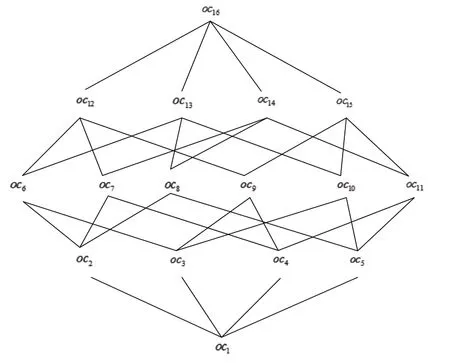
图1 表1的NONPSE-概念格Fig.1 NONPSE-concept lattice of Table1

由NONPSE-概念定义可知，任给一个对象子集X⊆G，都存在一个NONPSE-概念(X,[,])与之一一对应.

3 基于负信息的属性导出必然-可能半三支概念

3.1 属性导出负必然-可能三支算子

定义9设(G,M,I)为一个形式背景，对于任意A∈P(M)，定义属性导出负必然-可能三支算子，简称NANPE-算子.

NANPE-算子有以下性质.

性质3设(G,M,I)为一个形式背景，对于任意A1,A2∈P(M)，有

3.2 属性导出负必然-可能半三支概念

定义10设(G,M,I)为一个形式背景，对于任意，则称为属性导出负必然-可能半三支概念，简称为NANPSE-概念，

NONPSE-概念与NANPSE-概念统称为负必然-可能半三支概念，简称为NANPSE-概念.

类似于NANPSE-算子，对于属性子集A⊆M，可以利用NANPSE-算子获得对象集G上的一个区间集这个区间集可将G分为3 部分：正域、负域，及边界域，并形成G的一个弱三划分.

记(G,M,I)的所有NANPSE-概念的集合为NANPSEL(G,M,I),定义其偏序关系为：对于任意

称NANPSEL(G,M,I)为(G,M,I)的属性导出负必然-可能半三支概念格，简称为NANPSE-概念格.定理2给出其上、下确界，证明同定理1，这里不再赘述.

定理3NANPSEL(G,M,I)是一个完备格，其上、下确界分别为

定理4ANPSEL(G,M,I)≅NANPSEL(G,M,I).

例4表1形式背景下所有的NANPSE-概念如表3所示，NANPSE-概念格如图2所示.

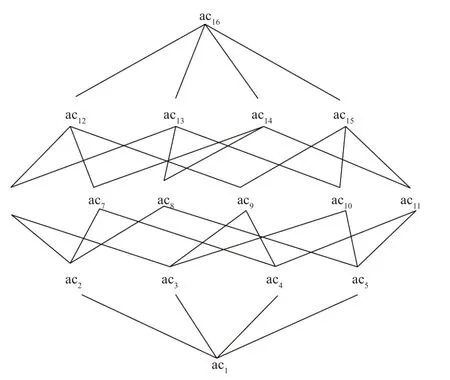
图2 表1的NANPSE-概念格Fig.2 NANPSE-concept lattice of table 1

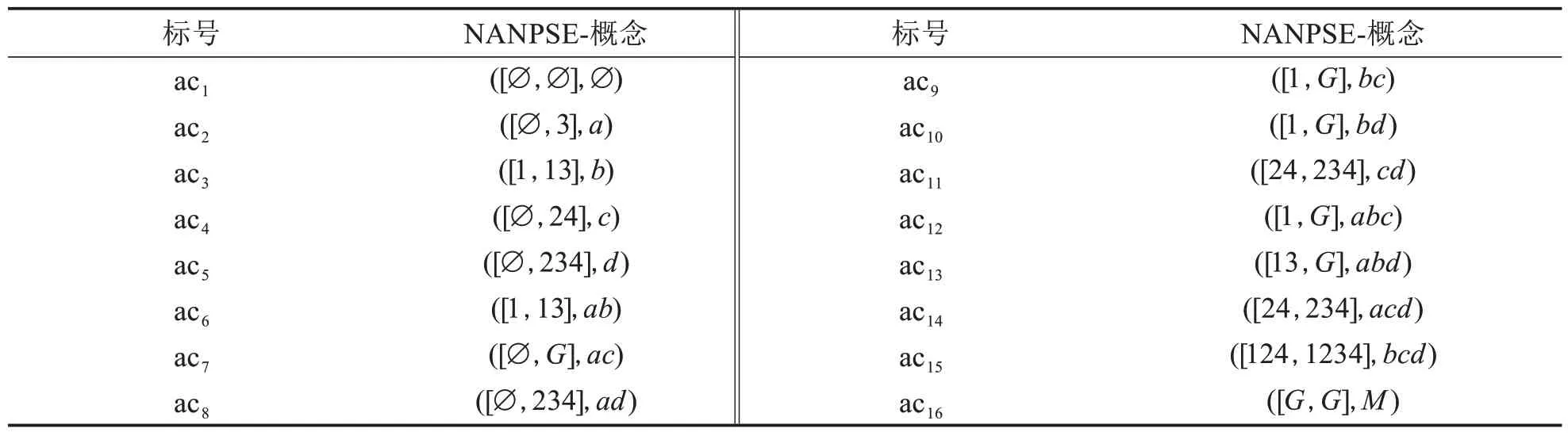
表3 表1 的NANPSE-概念Tab.3 NANPSE-concept of table 1

以概念([1,G],bc), ([1,G],bd)为例解释NANPSE-概念的语义.概念([1,G],bc)表明：学生1 一定不会解决问题b或c，且不会解决问题b和c的学生可能在G中；概念([1,G],bd)表明：学生1一定不会解决问题b或d，且不会解决问题b和d的学生可能在G中，进一步可以说明，学生1 一定不会解决问题b，也符合概念([1,13],b)的语义；另一方面，，可以看出，即不会问题c的同学一定不会d，故概念([1,G],bc)， ([1,G],bd)内涵不同外延却一致.

4 例子

在第二、三节定义负必然-可能三支半概念，它既能对数据信息进行有效表述又避免经典形式概念下由于强对应关系造成的信息丢失.为说明所提出负必然-可能三支半概念的实用性，在某小学四年级随机挑选20名学生进行案例分析，通过测试题的形式对他们解决问题的能力进行检验，其中测试题目为：a.计算；d.解方程；e.一个数的比它的多60，求这个数.具体测试结果如表4，学生正确解决该问题记为1，否则为0.

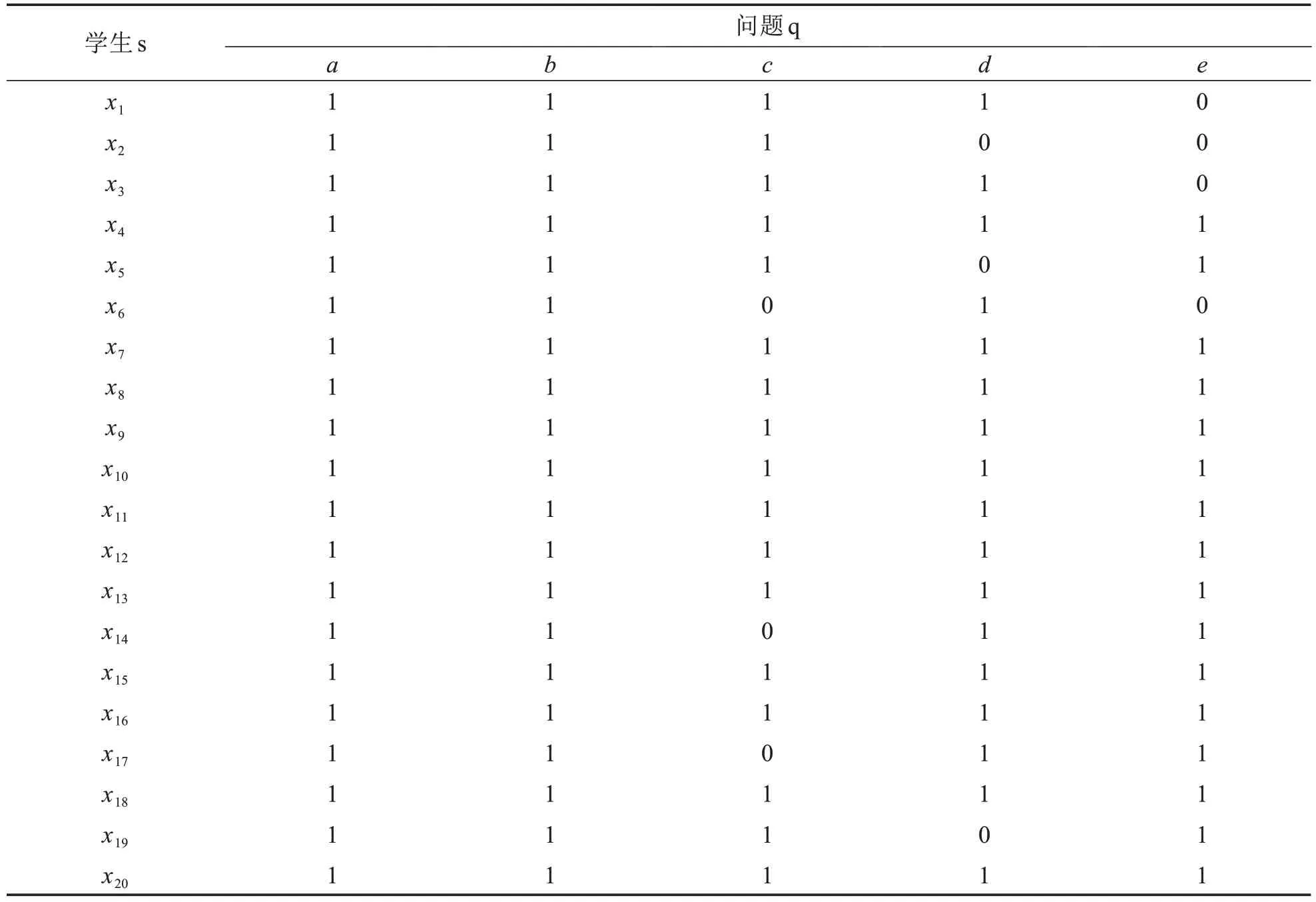
表4 测试结果Tab.4 Test result

由于学生全部做对和全部做错在的研究中不具有参考价值，故删去全部正确、全部错误的数据，由于存在相同测试结果，为表示简便，令[x1]q={x1,x3}，[x2]q={x2}，[x5]q={x5,x19}，[x6]q={x6}，[x14]q={x14,x17}，最终处理后的测试结果所产生的形式背景如表5～6 所示，其中“1”表示学生会解决此问题，“0”则表示学生不会解决此问题.

表5 形式背景(G,M,I)Tab.5 An formal context (G,M,I)

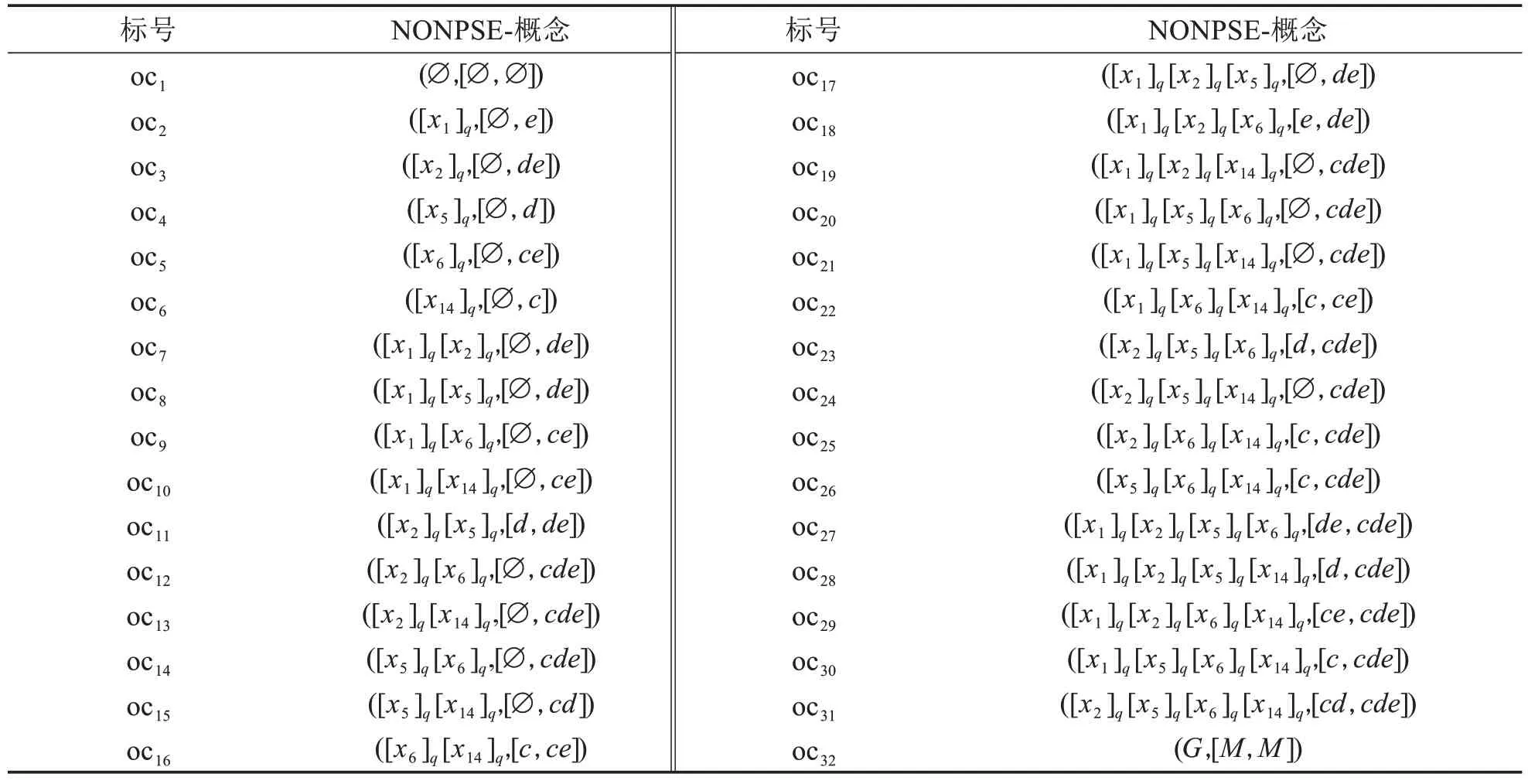
表6 表5 的NONPSE-概念Tab.6 NONPSE-concept of Table5

受粗糙集思想的启发，每一个NONPSE-概念的内涵都可以看成由正域POSX=、负域NEGX=M-组成的区间，而对于某个问题而言，教师在教学过程中更容易关注到学生不确定掌握的问题，即边界问题，那么这些问题是否需要进一步讲解就成为教师需要关注的方向，故引入问题判别参数（q-discriminant parameter）dαq的定义.

定义11设为NONPSE-概念，其边界问题为，对任意问题m∈M，其判别参数dαq为

其中：|oc|为所有NONPSE-概念的个数，|X|为概念外延所含对象个数，如概念oc7：([x1]q[x2]q,[∅,de])其外延所含对象个数，若dαq≥α则说明问题需要被老师关注，采取进一步的措施解决该问题.

在案例中，令α=0.5，dαq(c)=0.47 ＞α，dαq(d)=0.58 ≥α，dαq(e)=0.72 ＞α，即问题d,e 存在一定难度，学生不能顺利解决该问题，需要教师采取进一步措施.问题与其判别参数的变化趋势如图3所示.

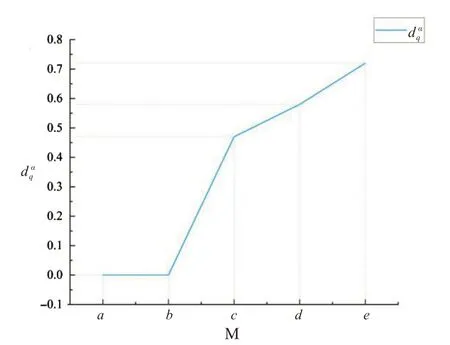
图3 问题判别参数d αqFig.3 Discriminant parameter of question d αq

图3 分析：由图中可以看出，dαq(d),dαq(e)＞α，即问题d,e需要被教师进一步解决.从知识层面来说，数学学科知识量大且语言抽象，思维方法具有层次性跃迁，会出现一个知识点讲授很多遍，学生不会做题的情况.故而，针对这些仍然存在困惑的问题就急需教师采取不同措施解决.

针对问题d，dαq(d)=0.58 ≥α，只有一部分同学对该问题存有困惑，并不需要在全班进行讲解，可以针对该问题制作微课上传至云平台，供学生自助取用；针对问题e，可以看出该问题的相关知识点学生掌握程度较低，可以对全班同学进行精准知识讲解，力求突破难点.根据布鲁姆的掌握学习理论的核心观点：若给足学生时间并采取适当的教学方法，几乎每个学生可以对所有内容达到掌握的程度.通过精准有针对性的辅导，不仅可以高效解决数据反馈的问题，而且能够针对具体问题采取强化措施，见表7.

表7 表5的NANPSE-概念Tab.7 NANPSE-concept of Table 5

而对于学生而言问题可以反应该学生对知识的理解程度，每一个NANPSE-概念的内涵都可以看成由POSA=、负域NEGA=G-组成的区间，教师在教学过程中应该注意到对某些问题似是而非的同学，即处于边界域的学生，为确定这些学生是否需要教师个性化辅导，故引入对于学生的判别参数（s-discriminant parameter）dβs的定义.

定义12设为NANPSE-概念，，对任意学生[xj]q∈G，其判别参数为

在案例中，令β=0.4，dβs([x1]q)=0，dβs([x2]q)=0.44，dβs([x5]q)=0.11，dβs([x6]q)=0.33，dβs([x14]q)=0，可以看出学生2需要教师进一步辅导.然而，学生是具有个体差异性的，个性化辅导便是弥补上述情况的有效手段.如：学生2对知识点的理解不够透彻，可以考虑进行课后作业辅导、精准考后分析等措施，做出适当的调整和补救，这样可以使得个性化辅导更有针对性，从而改善学困生的学习状态，与此同时，dβs([x2]q)＞dsβ([x6]q)＞dsβ([x5]q)，即学生2急需老师关注，学生6，5，19次之，教师采用个性化辅导也可加强师生之间的联系，使老师得到及时的反馈，增强学生的幸福感.

目前，对于学困生的教育效果直接影响素质教育的深化及新课程改革目标的实现，导致对学困生教育的关注度越来越高，因此教师需在教学实践和日常生活中对这类学生因材施教，以推动素质教育的进一步发展.

5 结论

在教育教学中的实际背景下，结合区间集，定义负必然-可能半三支概念，从负背景上拓宽半三支概念的语义.而对象和属性作为两种不同的研究角度，生成的两种负必然-可能半三支概念应用场景也有所不同，对象导出负必然-可能半三支概念从对象出发，对属性进行划分，属性导出负必然-可能半三支概念从属性出发，对对象进行划分，因此如何结合上述研究成果，对负必然-可能半三支概念的应用做进一步研究也很有意义.同时必然算子与可能算子与粗糙集的上、下近似密切相关，故如何将其与粗糙集理论相结合也很有必要.在概念认知学习中，通过概念对事物进行认知也是一个值得研究的课题，由于负必然-可能半三支概念的外延与内涵没有严苛的双向对应，能否能在概念认知学习过程中取得较好的效果也值得讨论.这些都是未来的研究方向.