一种基于多维数字锯齿混沌的伪随机序列发生器及其性能分析
2023-12-25王传福吕植成
王传福 吕植成
(湖北经济学院信息工程学院 湖北武汉 430205)
混沌是一种复杂的非线性动力学系统,具有初值敏感性、轨道遍历性、非周期性等特点[1],由于这些特性与香浓提出的混淆与扩散相一致[2],因此利用混沌系统被认为是构造伪随机序列的一种新型设计方法。混沌系统可被分为连续混沌系统和离散混沌系统。对数字系统来说,连续混沌系统需要先离散化再数字化。连续混沌系统离散化常用的方法有欧拉法[3]和龙格库塔法[4]。与连续混沌系统相比,离散混沌系统的数字化更简单,并且更适用于数字伪随机序列发生器。但由于有限字长效应,数字混沌系统的混沌特性逐渐退化,并且表现出短周期性和多周期性[5-8]。混沌系统也被分为高维混沌系统和低维混沌系统。低维混沌系统实现效率高,资源消耗小。常用的低维混沌系统有Logistic映射[9],Henon映射[10],锯齿混沌[11]等。低维数字混沌系统的混沌特性退化较为严重,输出序列难以保证具有较大的周期[5,7,8]。高维混沌系统具有更复杂的非线性动力学行为,但具有硬件实现资源消耗大,运行速度低等缺陷。
为了使数字混沌序列发生器利用较少的计算复杂度产生具有较大周期的输出序列,多种简单数字混沌相结合的形式得到了深入的研究。与其它低维离散混沌相比,锯齿混沌具有非常简单的运算形式,并且其输出值在0和1之间,容易进行数字化处理。锯齿混沌的多种组合方式同时得到了深入的研究[12-16]。在硬件实现中,乘法运算占用硬件资源较多,且对硬件实现的速度性能有较大的限制[17-21]。
为了进一步提高输出序列的周期,本文在保证低资源消耗的前提下,利用简单的锯齿混沌为基本模型,设计出一种基于多维数字锯齿混沌的伪随机序列发生器。为了减少计算复杂度,多维数字锯齿混沌的参数都被定义为2的倍数。与其它多种组合的锯齿混序列发生器相比,一种简单的非线性除法运算被引入,可以明显增加伪随机序列的周期,并且更逼近最大周期的上限。经验证,本文设计的基于多维数字锯齿混沌的伪随机序列发生器输出序列的周期得到极大提升,并能通过NIST套件的随机性测试。本文第一部分介绍了数字锯齿混沌。第二部分提出了一种基于数字多维锯齿混沌的伪随机序列发生器。最后一部分对全文做了总结。
一、数字锯齿混沌
锯齿混沌是一种广泛运用的混沌系统,它被定义为:
由于锯齿混沌输出的全是小数,因此数字化后的锯齿混沌更利于硬件实现。小数xn的N比特定点数n表示为
式(1)转化到数字域上,并两边同乘2N可以得到式
将式(2)带入式(3)可以得到数字锯齿混沌(4)
数字化的锯齿混沌的最大周期Tmax=M/4。常用的数字锯齿混沌的参数如表1所示。

表1 数字锯齿混沌的参数
数字锯齿混沌输出值是整数值。在进行随机性测试前需要被量化。量化方法为:输出值大于等于M/2,输出为1;输出值小于M/2,输出为0。NIST 套件是美国国家标准与技术研究院测试伪随机序列随机性的标准检测工具,共有15种测试项目。当NIST 套件输入为Q 个K 比特长的序列时,返回实验结果u-value 和ration。当u-value 大于10-4时,说明所有待测数据能够通过NIST 套件测试,并且该测试序列具有较好的随机性。本文针对β= 30517578125,M= 235的数字锯齿混沌,选取其产生的100 条长度为2000000 比特的序列进行测试。数字锯齿混沌输出序列的随机性测试如表2所示。
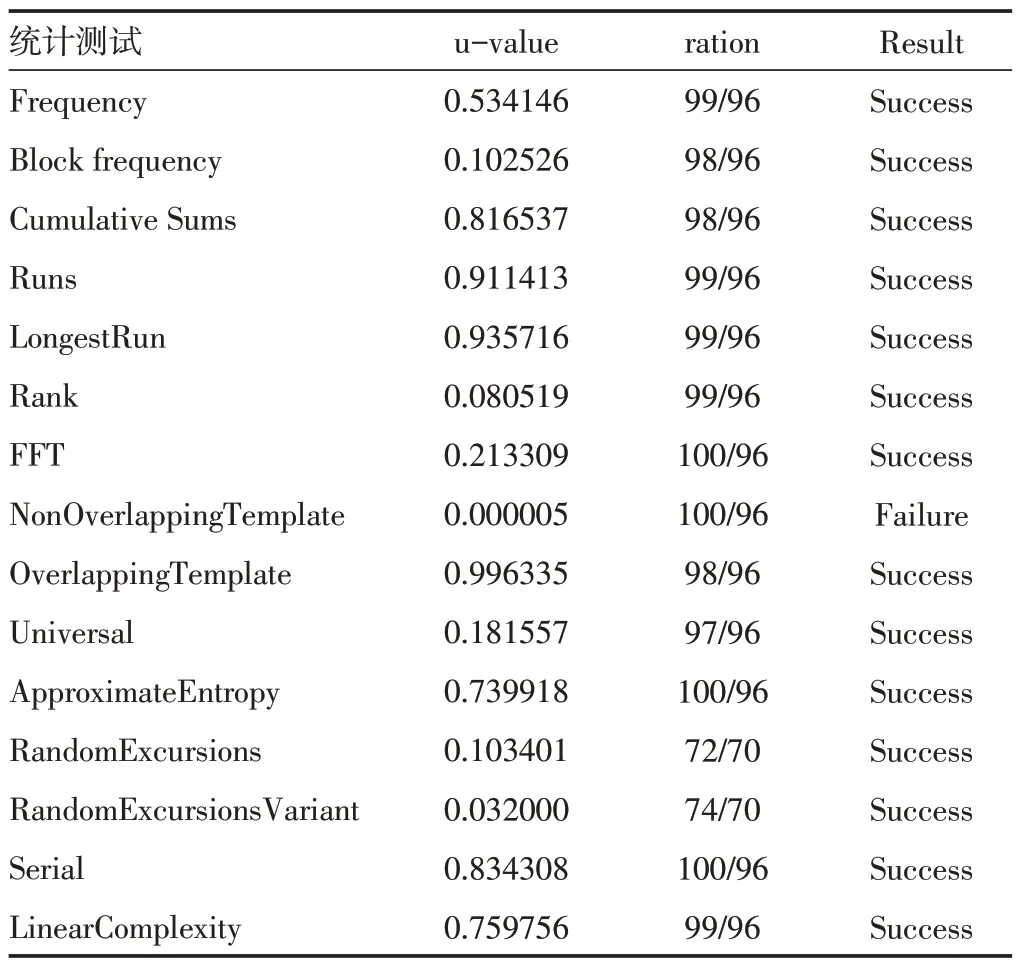
表2 当β = 30517578125,M = 235时,数字锯齿混沌的随机性测试
在表2中,NonOverlappingTemplate的u-vale明显小于10-4,未能通过NIST 套件测试,其输出序列的随机性较低。利用FPGA进行硬件实现的资源消耗如表3所示。

表3 数字锯齿混沌硬件资源消耗表
吞吐量是输出比特与主频的乘积。数字锯齿混沌每个周期只能输出1 比特序列。因此,利用FPGA 实现的数字锯齿混沌的吞吐量为72.97M/S。
二、基于数字多维锯齿混沌的伪随机序列发生器
虽然数字锯齿混沌的伪随机特性并不理想,但是数字锯齿混沌系统十分简单。因此,本文就以数字锯齿混沌为基本模型构造了多维数字锯齿混沌,并分析了基于数字多维锯齿混沌的伪随机序列发生器的性能。
(一)定点数上的快速算术运算。算术运算主要包括加法运算,减法运算,乘法运算和除法运算。除法运算相对比较繁琐。因此,在运算过程中除法运算需要尽量避免。乘法是常用的非线性运算操作,但是乘法计算的复杂度较高,容易产生更多资源消耗。若以2的倍数作为乘数或除数时会更为简单,当乘数是2的倍数时,乘数2n使被乘数左移n位,低位由0填补;当除数是2 的倍数时,除数2n使被除数右移n位,高位由0 填补。乘法和除法的运算可转化为移位运算。因此,计算量可以得到较大优化。与减法相比,加法运算更容易,复杂度更小。因此,本文选用加法运算和2的倍数的乘法运算及除法运算来设计基于数字锯齿混沌的伪随机序列发生器。
(二)多维数字锯齿混沌。本文将多个一维锯齿混沌组合形成多维的锯齿混沌迭代方程。多维锯齿混沌方程为:
其中M= 1,Pn被定义为(xm-1n,xm-2n,xm-3n,xm-4n, ···,x2n,x1n),β是m×m的矩阵。
由表1可知,每个数字锯齿混沌周期性与β的周期性有关,为增大输出周期,减少计算复杂度,式(6)β中的元素被固定为2 的指数。为了进一步降低计算复杂度,β中每行至多有两个非零元素。根据以上考虑,特殊的参数矩阵β如下所示
参数矩阵β中元素。
(三)周期分析。周期是伪随机序列非常重要的一个性质。将式(2)带入式(5)中进行数字化处理,可得到多维数字锯齿混沌。本文以m= 6 时的多维数字锯齿混沌为例,进行周期分析。不同精度下的6维数字锯齿混沌序列发生器输出序列周期如表4所示。
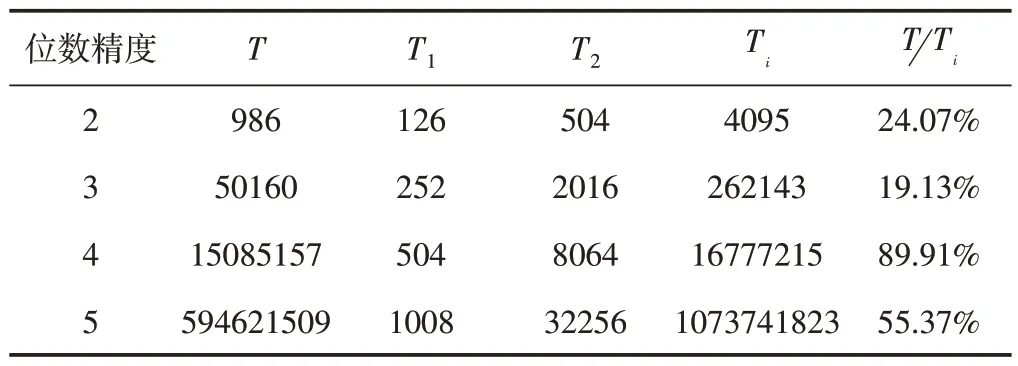
表4 6维数字锯齿混沌输出序列周期分析
在表4中,T为本文提出的6维数字锯齿混沌输出序列的周期,随着位数精度的增大,伪随机序列T的周期急剧增大。T1为一维组合锯齿混沌输出序列的周期[16],T2为加入了扰动的一维组合锯齿混沌输出序列的周期[17]。Ti是同等条件下输出序列周期的上限。由参数m和N构成的组合锯齿混沌能够产生的大周期为2Nm- 1。对三种锯齿混沌输出序列的周期性进行比较,利用本文方案产生序列的周期T明显比T1和T2大,并且更接近理想周期。
(四)随机性分析。本文对6维数字锯齿混沌输出的序列进行了随机性测试。将输出的x1n序列分为100 条周期长度为2000000的多组序列,一同进行NIST套件测试。为了与表2进行对比,系统精度N分别选取为12、23和35。
由表5可知,当系统精度N分别选取12、23和35时,输出的序列都通过了NIST 套件的测试。当N为35 时,在与表2 相同精度下,6维数字锯齿混沌输出序列的u-value明显高于表2中的数值,该数据表明6维数字锯齿混沌输出的序列具有更高的随机性和安全性。
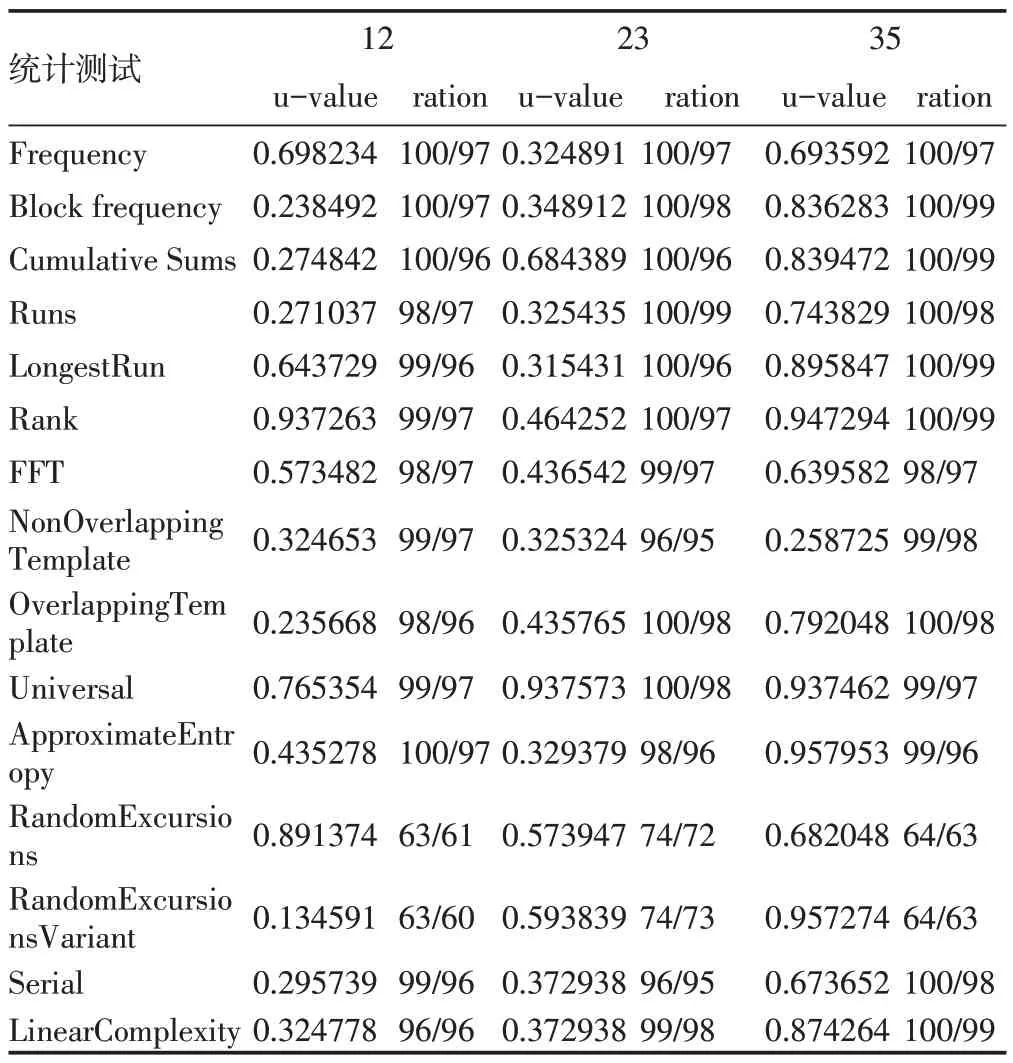
表5 x1n的随机性测试

表6 当N = 35时,6维数字锯齿混沌硬件消耗
(五)硬件性能分析。数字锯齿混沌包含乘法运算,随着计算精度N的增加,硬件资源消耗急剧增大。在同样系统精度N与迭代次数n的情况下,本文提出的6维数字锯齿混沌中的两个加法运算可以在同一个时钟周期内实现,在硬件实现上可以并行运算,具有非常高的并行运算效率。其它两种方案是顺序计算的结构[16,17],需要多个加法运算周期。因此,本文提出的6维数字锯齿混沌硬件实现速度比其它两种方案更快且资源实现更小。在N= 35时,本文提出方案硬件消耗和输出序列吞吐量如下表所示。
(六)密钥空间分析。密钥空间越大抵抗暴力攻击的能力越强。目前,密钥空间为2128时足够抵抗现有计算机的暴力攻击。在多维锯齿混沌(5)中,N和m是两个可根据实际情况更改的参数,通过改变N和m可以改变密钥空间的大小,多维锯齿混沌(5)密钥空间为2Nm。
(七)实现方法。在硬件实现方面,本文选用的FPGA芯片是Altera 厂家的CycloneII-EP2C70F896C8 芯片。仿真软件为QuartusII,且版本号为13.0。测试所用的计算机为Win10系统,芯片为Intel CoreI5-4460,CPU 为3.20GHz。在NIST 测试方面,NIST测试软件型号为STS-2.1.2,Block frequency 测试中的分块长度为128,NonOverlappingTemplate 测试中的分块长度为9,OverlappingTemplate测试中的分块长度为9,ApproximateEntropy测试分块长度为10,Serial测试中的分块长度为16,LinearComp lexity测试分块长度为500。
三、结语
数字化后的锯齿混沌的随机性并不理想,并且输出序列的周期随参数选取的不同而不同,具有多周期和短周期特性。本文利用简单的锯齿混沌构造出了一种基于数字多维锯齿混沌的伪随机序列发生器,该伪随机序列发生器具有并行结构,硬件实现资源消耗较少,输出序列周期大,且每个输出序列随机性都通过了NIST套件的测试,结果显示该输出序列具有较高的随机性和安全性。
