采用双RBF神经网络控制的机械手末端位姿研究

2023-12-24罗玉梅王丽娟

中国工程机械学报 2023年5期

罗玉梅，王莹，王丽娟

（郑州工业应用技术学院机电工程学院，河南郑州 451100）

机械手具有自动化程度高、定位精度高和可以连续工作等优点，广泛应用于食品包装、汽车制造、航空探测及数控换刀等领域［1］。机械手主要分为串联和并联2 大类。串联机械手的应用相对较早，技术也相对成熟，在市场中占据一定的优势。但是，串联机械手在各个关节安装过程中，会造成误差累积，导致机械手定位精度下降。与串联机械手相比，并联机械手可以避免上述问题。

随着对并联机械手的深入研究，许多学者在机械手上采用不同的控制装置，取得了一些研究成果。文献［2-3］对并联机械手运动轨迹增广PD（proportion differentiation）控制方法进行了研究，搭建了并联机械手实验平台进行仿真验证，从而降低了并联机械手运动轨迹跟踪误差。文献［4-5］对2 自由度并联机械手控制方法进行了研究，设计了H∞+动力学前馈控制方法，通过仿真验证并联机械手输出误差，提高了机械手末端执行器定位精度。文献［6-7］对并联机械手控制系统进行了测试，设计了机械手模糊控制方法，能够较好地实现运动位姿的跟踪，使控制系统反应速度加快。上述研究提高了并联机械手控制精度。但是，人们对产品的精度要求越来越高，现有控制系统已经不能满足高精度机械手定位的需求。为提高机械手定位精度，本文设计了双径向基函数（radial basis function，RBF）神经网络控制器，采用数学软件Matlab 对并联机械手运动位姿进行仿真，对比单RBF 神经网络控制器的输出效果，为深入研究并联机械手末端执行器定位精度提供理论参考。

1 并联机械手

本文主要研究用于数控机床刀架上的并联机械手，机械手的运动学模型如图1所示。

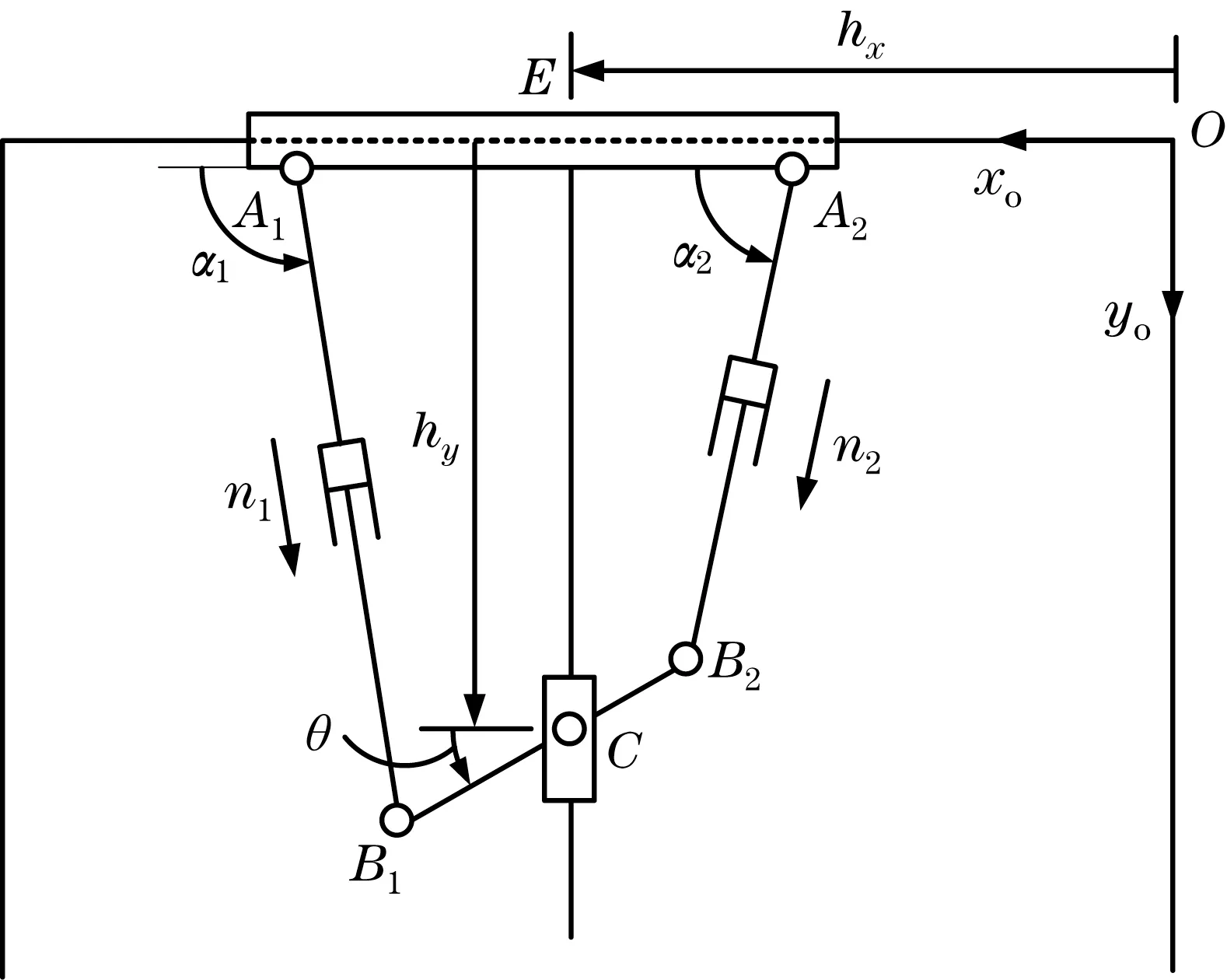
图1 平面并联机械手Fig.1 Planar parallel manipulator

由图1可知，支腿通过A1、B2处的2个旋转接头和执行器将移动平台连接到滑块上。假设机械手的结构是对称的，为了便于分析，在固定基座的拐角处附加了一个固定的参考坐标系O-x0y0，x0轴沿着支腿的方向。移动平台的姿态（位置和方向）由3个变量hx、hy和θ控制，其中hx和hy为C点相对于参考坐标系O-x0y0的位置，θ是x0轴正方向与B1B2的夹角。在本文中，逆时针方向的角度都被认为是正值。

变量di为第i个执行器的行程，当i=1，2 时，di为点Ai和Bi之间的距离；当i=3时，di为点O和E之间的距离。因此有d1=A1B1，d2=A2B2和d3=OE。前2 个执行器的运动范围为d1，d2∈［dmin，dmax］。垂直导轨连接在E处的滑块中间，移动平台通过中心点C处的执行器和旋转接头连接到垂直导轨上。因此，EAi=a，CBi=b。由于垂直导轨，移动平台相对于滑块有2 个自由度：一个平移平行于y0轴，一个绕垂直于运动平面的轴旋转。滑块沿x0轴有一个平移自由度。因此，机械手作为一个整体，相对于基座有3个自由度［8］：

式中：λ为任务空间顺序；ν为连接数；η为关节数；ei为第i个关节的自由度。

2 机械手运动学

2.1 逆向位置分析

对于逆位置运动学，给出了运动平台的姿态（hx，hy，θ），并求出了驱动关节变量di（i=1，2，3）。根据图1 中机械手的几何结构，可以得到支腿矢量回路方程：

式中：ai=EAi=（-1）i+1aiλ；bi=CBi=［bi，xbi，y］T=（-1）i［bcosθbsinθ］T；h=EC=hyjλ；di=AiBi=dini=［di，xdi，y］T；iλ、jλ分别为x0轴和y0轴的单位向量；ni为平行于AiBi的单位向量。

将ai代入式（2），可以推导出

此外，从支腿分析hxiλ=d3iλ可以得到d3=hx。

2.2 正向位置分析

正向位置运动学是求出一组给定的驱动关节变量di（i=1，2，3）对应的运动平台的位姿（hx，hy，θ）。当i=1和i=2时，式（3）可以变换为

式中：cosθ=（）/2ab；sinθ=（）/4hyb。

根据三角函数sin2θ+cos2θ=1，可以得到hy中的一元六次多项式：

式（5）可以变换为

式中：q=。

已知q（以及由此得到的hy），则变量θ的唯一值可以由式（4）计算得到。因为q≥0，所以只有式（6）的正解是可接受的。每一个正解对应于hy的2 个实解。因此，机械手的2 个装配模式相对于x0轴对称。

3 控制器设计

3.1 控制系统描述

并联机械手n关节运动方程表达式［9-10］为

式中：q为关节角位移；M(q)为惯性矩阵；Vm(q，q′ )为离心力和哥氏力矩阵；G(q)为重力矩阵；τd为控制力矩。

在机械手运动控制系统中，死区可以定义为

式中：u为信号输入；g（u）、h（u）为非线性函数；τ为死区输出。

假设g（u）和h（u）在变化区间内为单调可逆递增函数，则死区可逆函数定义为

因此，可以得

为了提高机械手运动位姿精度，采用神经网络补偿器对并联机械手运动轨迹进行补偿，其控制系统结构如图2 所示。图中，qd为机械手运动轨迹，q为实际运动轨迹。

图2 并联机械手死区补偿控制系统Fig.2 Dead time compensation control system of parallel manipulator

3.2 双RBF神经网络控制器

神经网络控制器由2个RBF 神经网络构成，一个用于预估机械手驱动的非线性环节，一个用于前馈通道的死区补偿，其补偿器的基本结构如图3 所示。图中，ω为输入信号，NN1 为神经网络1，NN2为神经网络2。

图3 RBF神经网络死区补偿控制器Fig.3 RBF neural network dead time compensation controller

补偿后机械手控制输入定义为

死区环节的可逆形式等价形式为

其中，

根据RBF神经网络逼近特性［11-12］可以推导出：

式中：ε（u）和εi（ω）为神经网络建模误差；W和Wi为期望权值；σ和σi为径向基函数输出值。

定义W1和Wi1为RBF 神经网络预估权值，采用RBF神经网络调整相应的控制环节，可得

定义Wκ=W-W1、Wiκ=Wi-Wi1为RBF 神经网络权值估计误差。

4 结果与分析

为了分析双RBF 神经网络控制器的并联机械手运动位姿跟踪效果，采用Matlab 软件对并联机械手跟踪效果进行仿真验证，并且与单RBF 神经网络控制器输出效果进行比较，仿真参数设置见表1。

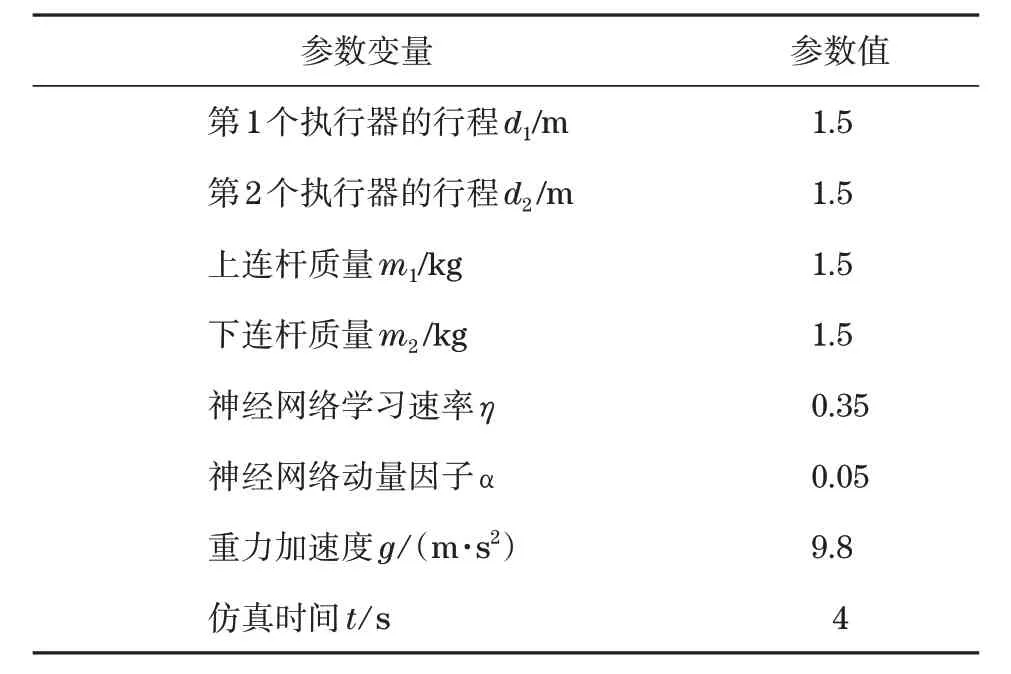
表1 仿真参数Tab.1 Simulation parameters

假设并联机械手运动位移方程式为=0.64（m2），角位移为θ=cos2πt（rad）。在无外界干扰状态下，并联机械手运动平台横向和纵向位移跟踪误差如图4 所示，并联机械手运动平台角位移跟踪误差如图5 所示。在有外界干扰状态下（θλ=10sin2πt（rad）），并联机械手运动平台横向和纵向位移跟踪误差如图6 所示，并联机械手运动平台角位移跟踪误差如图7所示。

图4 无外界干扰状态下并联机械手运动平台位移跟踪误差Fig.4 Displacement tracking error of parallel manipulator moving platform without external interference

图5 无外界干扰状态下并联机械手运动平台角位移跟踪误差Fig.5 Angular displacement tracking error of parallel manipulator moving platform without external interference

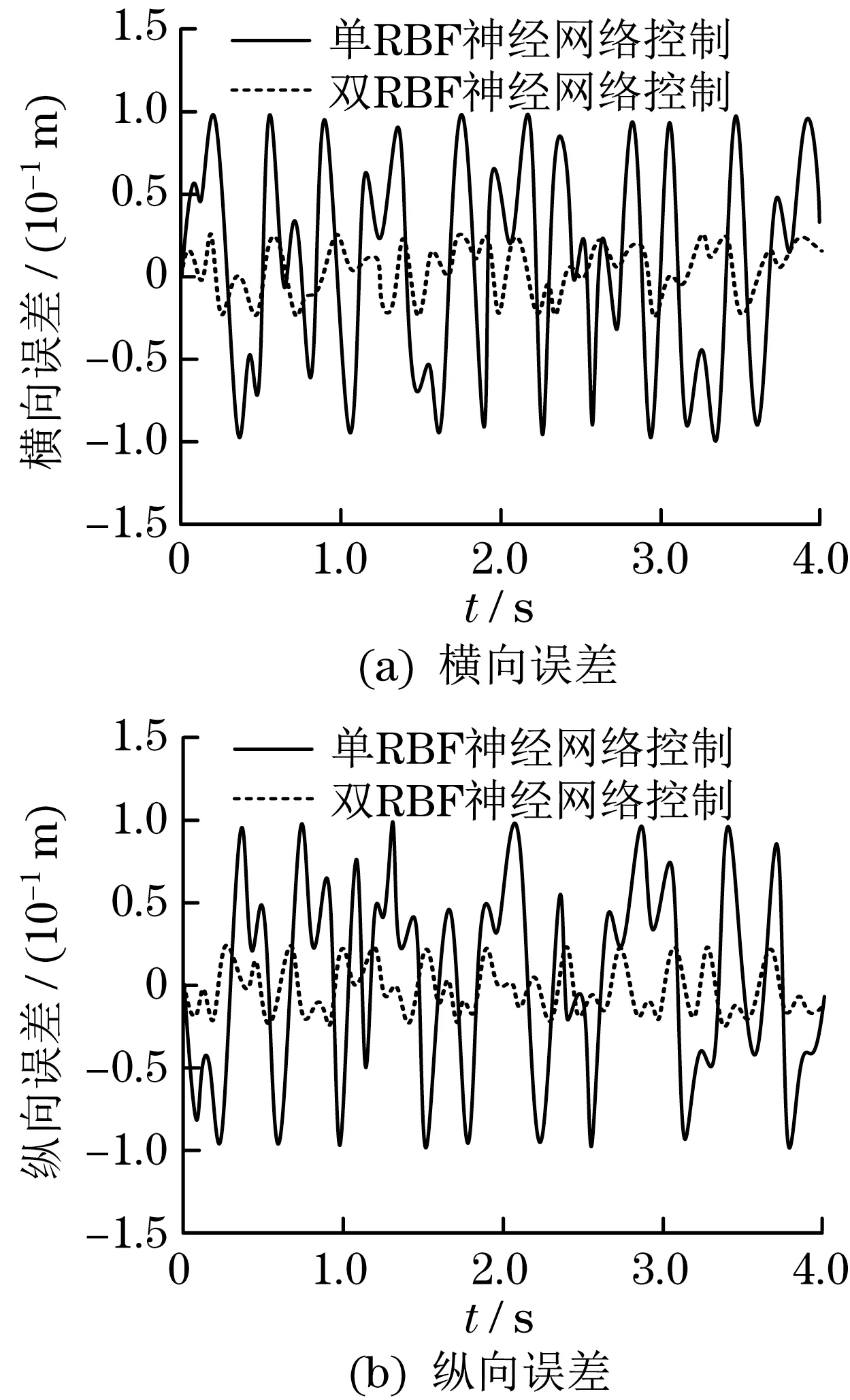
图6 有外界干扰状态下并联机械手运动平台位移跟踪误差Fig.6 Displacement tracking error of parallel manipulator moving platform with external interference

图7 有外界干扰状态下并联机械手运动平台角位移跟踪误差Fig.7 Angular displacement tracking error of parallel manipulator moving platform with external interference

由图4和图5可知，在无外界干扰状态下，采用单RBF 神经网络控制器和双RBF 神经网络控制器，并联机械手运动平台横向和纵向位移跟踪误差范围分别为［-0.05，0.05］ m 和［-0.025，0.025］ m，角位移跟踪误差范围分别为［-0.06，0.06］ rad 和［-0.04，0.04］ rad。

由图6和图7可知，在有外界干扰状态下，采用单RBF 神经网络控制器和双RBF 神经网络控制器，并联机械手运动平台横向和纵向位移跟踪误差范围分别为［-0.1，0.1］ m 和［-0.025，0.025］ m，角位移跟踪误差范围分别为［-0.12，0.12］ rad 和［-0.04，0.04］ rad。

在同等条件下，采用双RBF 神经网络控制器，并联机械手控制反应速度较快，能在线进行死区补偿，跟踪误差范围较小，可提高并联机械手位姿定位精度，从而提高数控机床刀具加工产品精度。