棉精梳机分离罗拉混合驱动系统优化
2023-12-24刘金儒李新荣师帅星
刘金儒, 李新荣, 王 浩, 师帅星
(1. 天津工业大学 机械工程学院, 天津 300387; 2. 天津市现代机电装备技术重点实验室, 天津 300387;3. 天津工业大学 纺织科学与工程学院, 天津 300387)
精梳机是纺纱过程中的重要设备,能够排除生条中的杂质和短纤维,进一步增加纤维的伸直度、平行度及分离度[1]。在精梳过程中,驱动系统使分离罗拉完成“倒转-正转-静止”的高速周期运动以实现对棉网的分离接合[2-3]。随着速度的不断提高,机构在运行时会产生较大的振动,造成机构稳定性与精度降低,进而影响精梳条质量。如何解决现有驱动方式传动链长、振动噪声大的缺点显得尤为重要。
分离罗拉的驱动主要有传统的多连杆或凸轮与差动轮系相结合、伺服电动机直接驱动及混合驱动的方式。任家智等[4-5]对传统驱动方式中的多连杆机构受到的惯性力进行分析,利用添加平衡配重的方法降低了机构的振动;丰田-特吕茨勒TCO12型精梳机采用伺服电动机代替现有的机械驱动方式[6],简化了传动链。但是上述方式还存在一些不足之处,如传统的机械驱动方式很难调整工艺参数,伺服电动机直接驱动的方式对电动机及控制系统的要求比较高,因此,一些研究将混合驱动理论应用到分离罗拉的驱动中,提出用2个伺服电动机作为动力源,通过齿轮传动系统进行运动合成来驱动分离罗拉的方案[7]。刘立东等[8]对比了1个常速电动机和1个伺服电动机作为动力源和2个伺服电动机作为动力源这2种方案发现,第2种方案对伺服电动机的要求更低。杨海鹏等[9]研究了双伺服电动机驱动分离罗拉的方案,通过优化分离罗拉运动规律以及合理分配伺服电动机的速度规律,减小了伺服电动机最大角加速度,从而降低对伺服电动机的要求。综上,以往的研究主要集中于如何降低伺服电动机的功率,为混合驱动理论在分离罗拉驱动上的应用奠定基础,但在如何优化齿轮传动系统以及如何避免刚性冲击与柔性冲击,从而使拟合的分离罗拉运动规律更为理想等方面的研究较少。
基于此,本文首先采用分段拟合的方法对分离罗拉运动曲线进行拟合,其次建立传动系统的动力学模型,并对系统中齿轮的齿数进行优化,然后规划伺服电动机的运动规律,最后通过仿真及实验验证设计的合理性,以期为分离罗拉混合驱动方式的完善提供理论指导与技术支撑。
1 分离罗拉驱动系统
1.1 分离罗拉运动分析
1.1.1 分离接合工艺及位移关键点分析
精梳机中机构的运动配合关系是靠装在锡林轴上的分度盘来确定的,分度盘沿圆周分为40等份,每等份表示1分度,锡林轴转1周,精梳机完成1个工作循环。在精梳过程中,分离罗拉先倒转将上个钳次输出的棉网倒入机内;然后在某1分度正转,使倒入机内的棉网尾部与梳理过的须丛前端叠合并向前输出,完成须丛的分离接合;最后,分离罗拉静止,不再输出棉网。图1示出分离罗拉在1个周期内的位移示意图。a分度时,分离罗拉开始倒转;b分度时,锡林末排针通过锡林与分离罗拉最紧隔距点,为使分离罗拉倒入的棉网尾部不被锡林末排针抓走,分离罗拉前段倒转量(Sb)不宜过大;c分度时,分离罗拉开始正转,该时间与给棉方式及开始分离时间有关;d分度时,分离罗拉正转速度达到一定程度,须丛开始分离,该时间与给棉长度、落棉隔距及钳板的运动规律等因素有关[10];e分度时,钳板运动到最前位置,须丛的分离工作完成,该时间与钳板运动规律有关[11],Sed为分离工作长度;f分度时,分离罗拉基本静止;g分度时,分离罗拉进入下一个运动周期,Sge为继续顺转量,为避免须丛全部倒出分离钳口使下个工作循环无法正常进行,应保证分离罗拉继续顺转量小于纤维长度。Sg为有效输出长度。
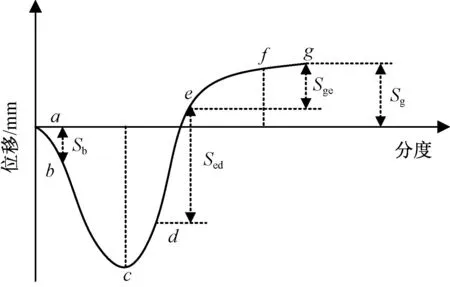
图1 分离罗拉位移示意图
分析精梳分离接合工艺,确定分离罗拉位移曲线的关键点,并根据某实际参数求解,得到分离罗拉运动过程中的位移关键点,分别为a(8,0)、b(12,-16)、c(18,-48)、d(20,-22)、e(30,10)、f(40,25)、g(8,26)。
1.1.2 分离罗拉运动曲线拟合
在分析分离罗拉运动规律及比较多个函数特点的基础上,采用3段七次多项式对分离罗拉运动曲线进行拟合[12]。设第1段位移(s1)、速度(v1)及加速度(a1)的方程如下:
(1)
式中:t为时间,s;Kh(h=0,1,…,7)为多项式的系数。
为使分离罗拉运动曲线的拟合结果更加精确,在拟合时需要保证分离罗拉位移曲线与关键点之间误差最小,即:
(2)
式中:s1(tx1)及y(tx1)分别为待拟合的第1段曲线及关键点在tx1处的位移值,mm;l1为第1段曲线中关键点的个数。
为避免分离罗拉产生刚性冲击和柔性冲击,得到更为理想的分离罗拉运动规律,在拟合分离罗拉运动曲线时,还需要保证分离罗拉在首末2点的速度及加速度均为零,则根据要求有:
(3)
式中:t0及tend分别为1个周期开始及结束时间,s;v3为第3段速度,mm/s;a3为第3段加速度,mm/s2。
将该曲线拟合问题转化为带有约束的最小二乘问题,用拉格朗日乘子法进行求解,列出拉格朗日函数如下:
(4)
式中,λ1、λ2为拉格朗日乘子。
对式(4)中各变量分别求偏导,并令偏导为0,然后求解方程组,便可得到第1段七次多项式的各个系数,采用类似的方法对第2段和第3段运动曲线进行拟合。取锡林转速为600钳次/min,即分离罗拉运动周期为0.1 s,计算各段系数后绘制分离罗拉运动规律,并将分离罗拉位移曲线和关键点进行对比,如图2所示。
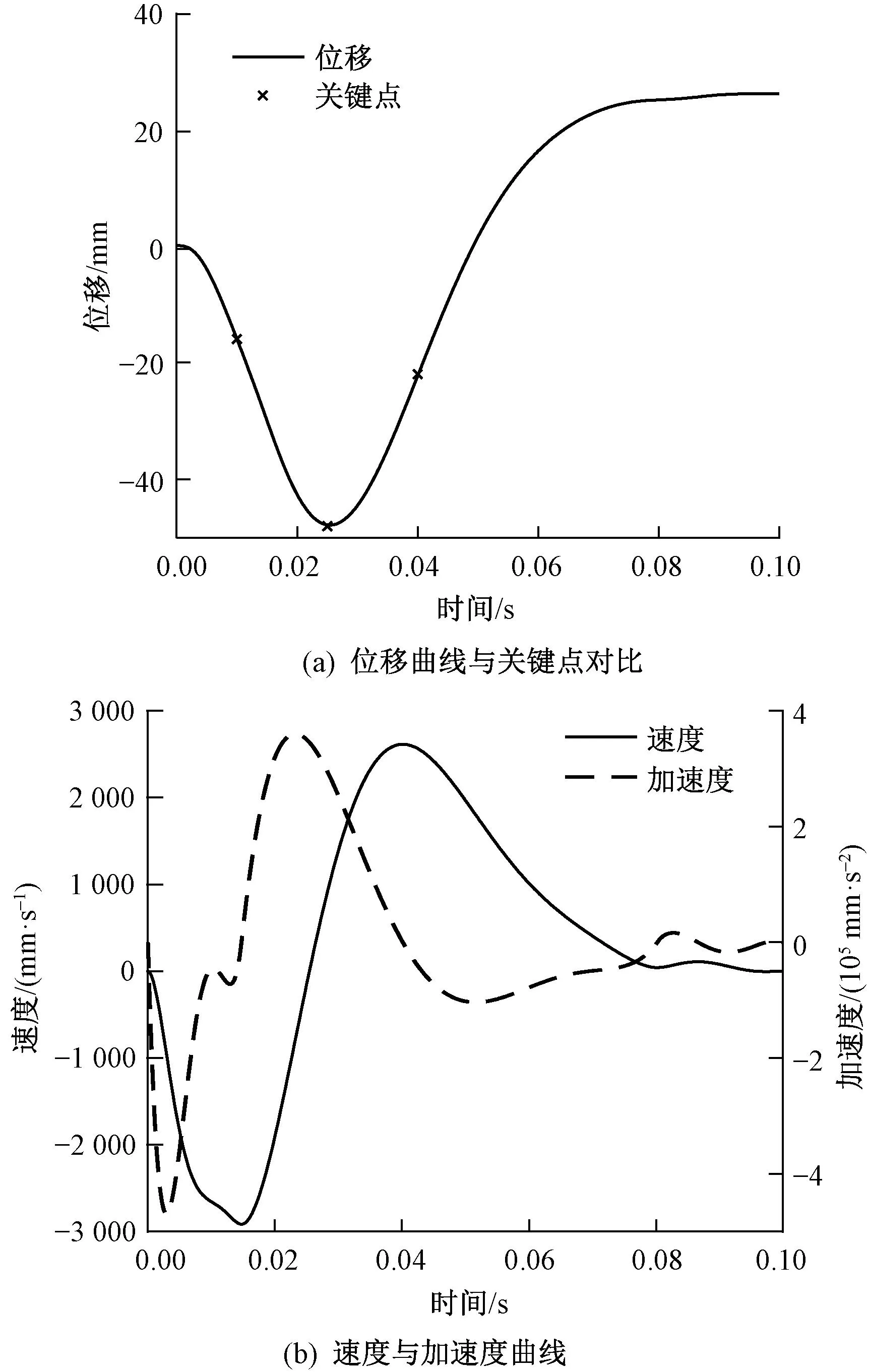
图2 分离罗拉运动规律
由以上结果可知,分离罗拉的位移曲线符合“倒转-正转-静止”的规律,与关键点的最大误差为0.30 mm,能够满足精梳分离接合的要求;速度和加速度曲线在首末2点的值均为0,避免了刚性冲击和柔性冲击,且在整个周期中连续变化无突变。这说明分离罗拉运动可以满足工艺要求且比较平稳,因此,拟合的分离罗拉运动曲线较为理想。
1.2 分离罗拉齿轮传动系统优化设计
1.2.1 动力学分析
由差动轮系和定轴齿轮组成的分离罗拉齿轮传动系统如图3所示。差动轮系由太阳轮s、太阳轮s′、行星轮pi(i=1,2,3)、行星轮p′i及行星架c组成,定轴齿轮由齿轮2、齿轮3、齿轮1及行星架c组成。扭矩从太阳轮s及齿轮1输入,经过传动系统由齿轮3输出。
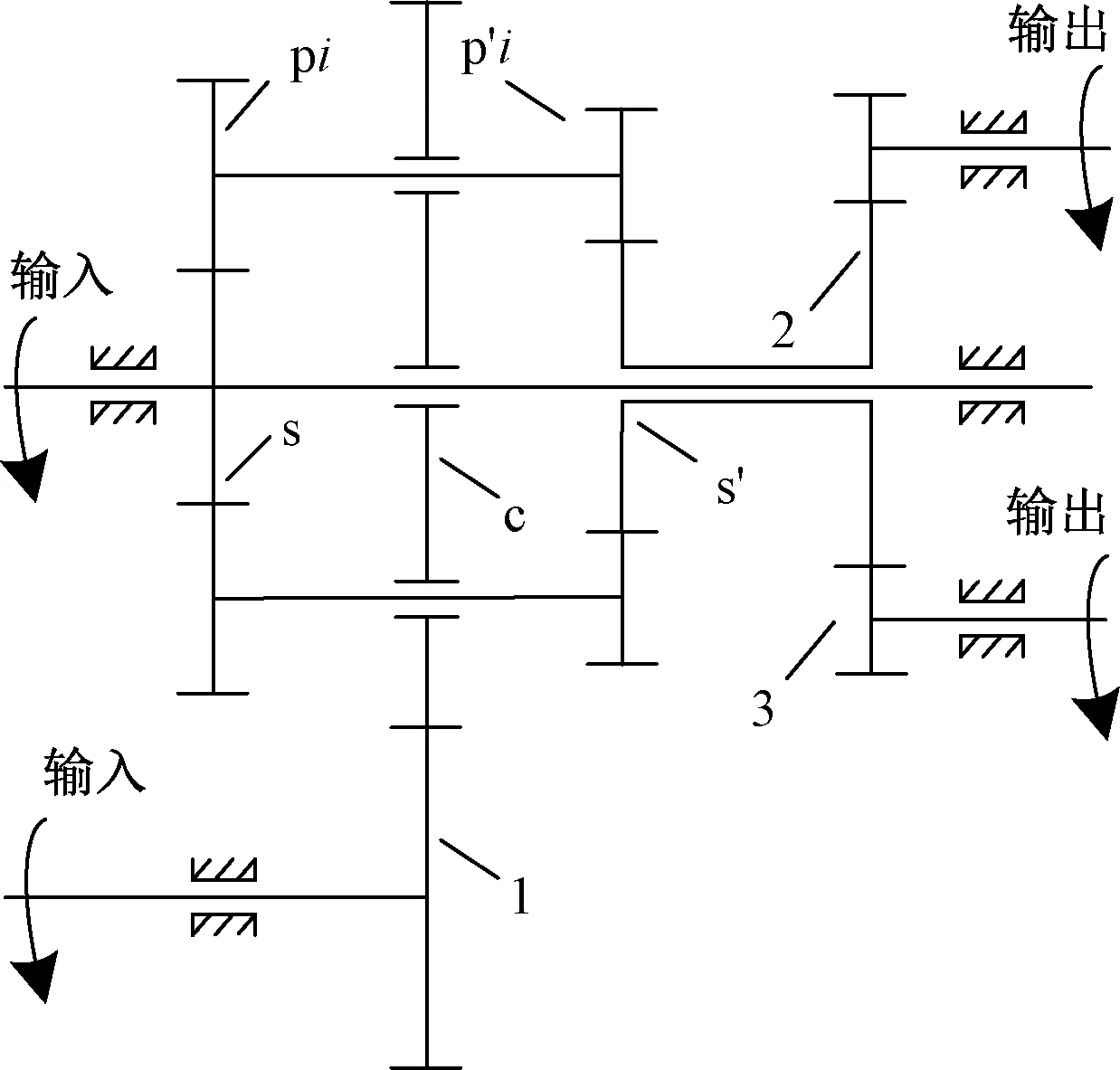
图3 分离罗拉齿轮传动系统简图
齿轮传动系统的动态响应可以反映系统的振动与噪声[13],为研究齿轮参数对系统振动的影响,基于集中质量参数法[14-15],将分离罗拉齿轮传动系统分解成差动轮系和定轴齿轮2个部分,用弹簧和阻尼器对齿轮啮合参数进行模拟,建立如图4所示的分离罗拉齿轮传动系统扭转动力学模型。图4(a)示出在行星架随动坐标系下建立的差动轮系扭转动力学模型。其中:kspi、cspi分别为太阳轮s与行星轮pi的啮合刚度和啮合阻尼;ks′p′i、cs′p′i分别为太阳轮s′与行星轮p′i的啮合刚度和啮合阻尼;kpip′i、cpip′i分别为行星轮pi与p′i连接轴的扭转刚度和扭转阻尼。图4(b)示出在固定坐标系下建立的定轴齿轮扭转动力学模型。其中:k1c、c1c分别为齿轮1与行星架c的啮合刚度和啮合阻尼;k23、c23分别为齿轮2与齿轮3的啮合刚度和啮合阻尼。

图4 分离罗拉齿轮传动系统动力学模型
分析系统中各构件的受力,根据牛顿第二运动定律得到分离罗拉齿轮传动系统中各构件的动力学微分方程如下。
行星架c:
(5)
太阳轮s:
(6)
太阳轮s′:
(7)
行星轮pi:
(8)
行星轮p′i:
(9)
齿轮1:
(10)
齿轮2:
(11)
齿轮3:
(12)
式中:Ij(j=s,s′,pi,p′i,c,1,2,3)为各构件的转动惯量,kg·m2;rbj为各构件的基圆半径,m;Mp1和Mp′1为行星轮p1及行星轮p′1的质量,kg;uj为各构件的扭转位移,m;Ts、T1及T3分别为作用在太阳轮s、齿轮1及齿轮3上的力矩,N·m;δspi、δs′p′i、δ1c及δ23分别为太阳轮s与行星轮pi、太阳轮s′与行星轮p′i、齿轮1与行星架c及齿轮2与齿轮3沿啮合线方向的弹性变形,m;αs及αs′分别为太阳轮s与行星轮pi之间及太阳轮s′与行星轮p′i之间的啮合角,rad;k2s′为太阳轮s′与齿轮2连接轴的扭转刚度,N·m/rad;c2s′为太阳轮s′与齿轮2连接轴的扭转阻尼,N·m·s/rad。其中:
(13)
现有的分离罗拉齿轮传动系统主要参数如表1所示。采用变步长的四阶龙格库塔法对所建立的微分方程组进行求解,得到现有传动系统中各齿轮的振动位移和振动速度后,代入相应参数计算得到各齿轮的振动加速度。

表1 现有的分离罗拉齿轮传动系统主要参数
1.2.2 优化设计
WW型差动轮系是分离罗拉齿轮传动系统的核心部分,本文选取WW型差动轮系中各齿轮的齿数作为分离罗拉齿轮传动系统优化模型的设计变量。振动加速度的均方根可以近似反映齿轮振动和噪声的大小,因此,为降低传动系统的振动,以系统中各齿轮的振动加速度均方根之和作为目标函数:
(14)
式中:üjJ(j=s、s′、pi、c、1、2、3;J=1、2、3、…、N)为各构件的振动加速度,m/s2;N为一段时间内振动加速度的取值个数。
约束条件为差动轮系必须满足的装配条件:同心条件、邻接条件与安装条件。如下式:
(15)
式中:ha*为齿轮齿顶高系数;q为配齿系数;s为zp1与zp′1的公约数;Z表示整数集。
采用优化算法进行求解,得到优化后各齿轮的齿数,分别为zc=95,zs=39,zs′=32,zpi=21,zp′i=28,z1=80,z2=87,z3=28。将优化后的参数代入动力学微分方程组,再次计算系统中各齿轮的振动加速度,并与优化前的各齿轮振动加速度进行对比,部分结果如图5所示。
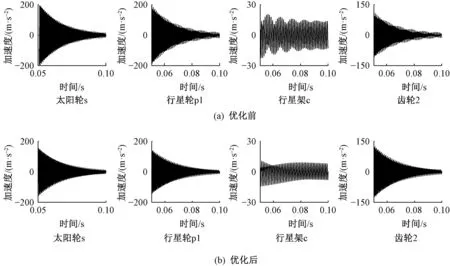
图5 优化前后传动系统中部分齿轮的振动加速度对比
从图5可以看出,优化后大部分齿轮的振动加速度得到不同程度地降低。经计算,传动系统中各齿轮振动加速度均方根之和比优化前减小了18.21%,达到了减振的效果。
1.3 伺服电动机运动规划
1.3.1 传动系统运动学分析
根据传动比关系,以构件a、H为输入,构件b为输出的差动轮系中的基本构件转速nb、na及nH满足下式:
(16)

在对差动轮系运动分析的基础上,考虑定轴齿轮的齿数,列出分离罗拉齿轮传动系统的运动学方程如下:
n3=-5.05ns-1.48n1
(17)
式中,n3、ns与n1分别为齿轮3、太阳轮s与齿轮1的转速,r/min。
1.3.2 速度分配
分离罗拉传动系统的动力源是2个伺服电动机,传动系统将2个伺服电动机的转速进行合成进而实现分离罗拉周期性的“倒转-正转-静止”,即齿轮3的转速等于分离罗拉转速,2个伺服电动机的转速分别与太阳轮s及齿轮1的转速相等。伺服电动机运行规律决定输出运动的正确与否,同时还需要考虑伺服电动机对于复杂运动的快速响应性,因此,有必要对伺服电动机的运动规律进行合理地规划。本文根据传动系统运动学分析结果,将分离罗拉的转速合理分配到伺服电动机上,同时为避免电动机频繁地换向,设计伺服电动机均为单向运行。
首先,将分离罗拉的转速分解为2个单向运行的转速之和,即:
n3=n++n-
(18)
式中,n+与n-分别为正向转速函数与反向转速函数,r/min。
由分离罗拉运动曲线可知,n3为六次多项式。为便于计算,设正向转速函数为六次多项式:
n+=b0+b1t+b2t2+b3t3+b4t4+b5t5+b6t6
(19)
式中,b0~b6为多项式的系数。
约束条件为n+始终为正,n-始终为负,即:
(20)
使用遗传算法进行求解,算得正向转速函数的各参数为:b0=2.27×103,b1=-9.8×104,b2=2.95×106,b3=2.55×107,b4=-1.55×109,b5=1.68×1010,b6=-5.76×1010。
用上述方法算得正向转速函数之后,根据式(18)得到反向转速函数,然后由式(17)可知,2个伺服电动机的转速可用下式计算:
(21)
根据上式代入相应参数,得到2个伺服电动机转速变化曲线,如图6所示。可以看出,与太阳轮s相连的伺服电动机转速始终为正,与齿轮1相连的伺服电动机转速始终为负,即2个伺服电动机均为单向运行,因此,对伺服电动机的运动规划满足设计要求。
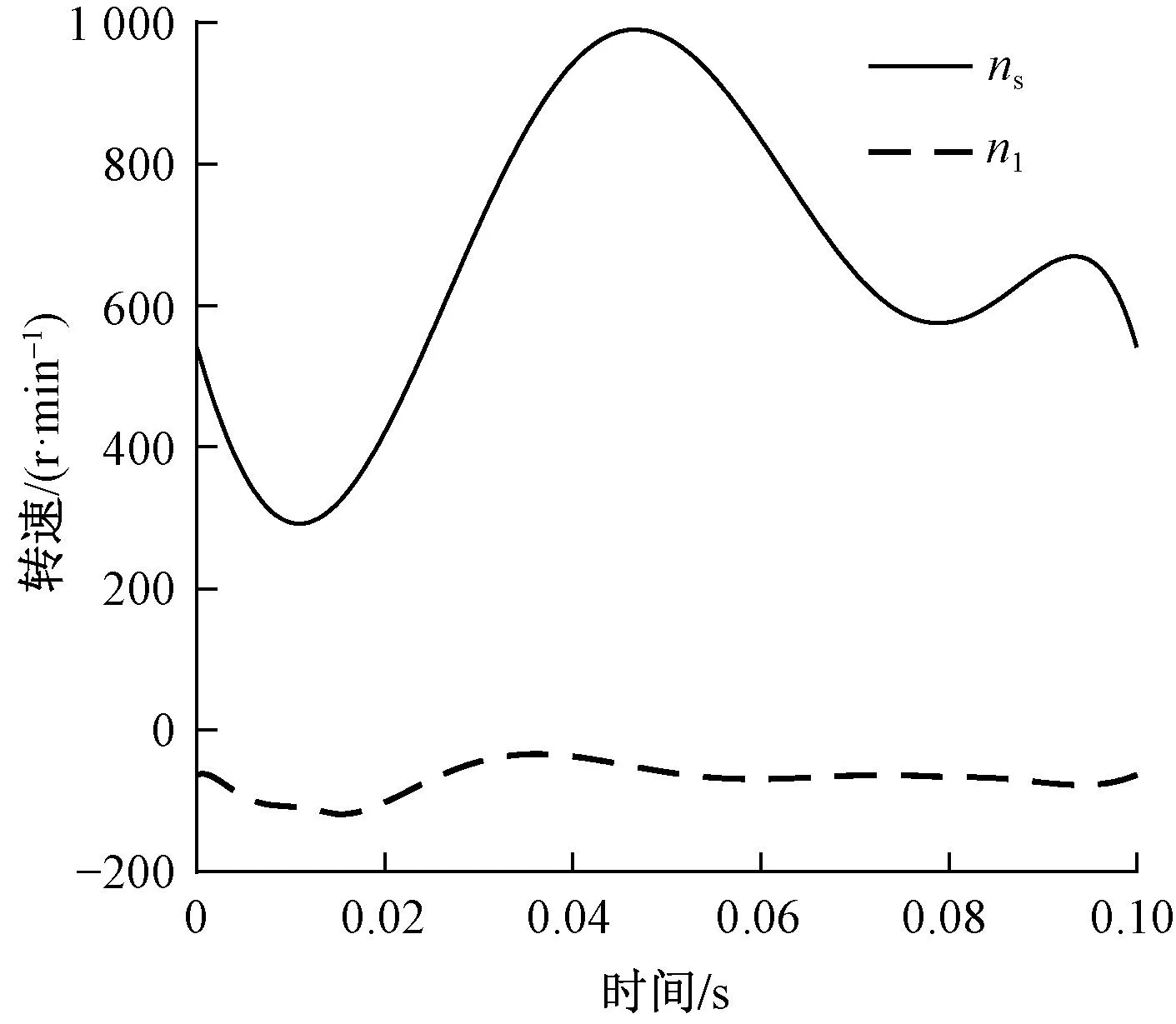
图6 伺服电动机转速
2 仿真及分析
在Pro/E中建立分离罗拉齿轮传动系统三维模型,然后将其导入ADAMS中,对约束副及驱动进行定义,最后进行仿真,得到分离罗拉的运动规律,将仿真得到的运动曲线与理论计算得到的运动曲线进行比较,结果如图7所示。可以看出,仿真得到的分离罗拉运动曲线与理论计算得到的运动曲线基本一致。说明所设计的分离罗拉驱动系统可使分离罗拉的运动满足工艺要求。另一方面,理论分析和仿真结果还存在一些误差,分析误差产生的原因,主要是理论计算没有考虑更多的因素,因此可以得到很好的结果,而ADAMS软件在仿真过程中考虑了摩擦力等因素,导致误差的产生。

图7 仿真与理论计算得到的分离罗拉运动曲线对比
3 实验验证
本文研究在多轴驱动的精梳机实验平台上进行验证,如图8所示。

图8 多轴驱动的精梳机实验平台
通过测量分离罗拉的位移来验证驱动系统能够保证分离罗拉的运动满足工艺要求,以及测量改变伺服电动机运动规律之后得到的分离罗拉位移来验证驱动系统能使分离罗拉的运动具有柔性。具体方法如下:编写程序使伺服电动机按照理论分析的速度运行,实验结束之后整理分离罗拉1个周期的位移数据,并将实验结果与仿真结果及理论计算值进行对比,以此验证分离罗拉运动的正确性;在此基础上调整关键点位置,重新计算伺服电动机的转速之后重复进行实验,得到不同的分离罗拉位移结果。
3.1 分离罗拉运动正确性验证
为进一步验证分离罗拉运动的正确性,在实验平台上进行实验后得到分离罗拉位移数据,并将其与仿真结果及理论计算值进行对比,结果如图9所示。可以看出,实验得到的分离罗拉位移曲线整体而言与理论计算以及仿真结果之间误差很小,验证了分离罗拉驱动系统可以代替传统的机械结构,克服了其传动链长、振动噪声大的缺点,完成对分离罗拉的驱动。而另一方面实验结果与理论计算在0.002及0.025 s附近误差较大,最大值分别为0.42及0.50 mm。误差较大的原因可能是分离罗拉在这2处附近的加速度很大,产生了较大的惯性力与惯性力矩,影响了机构运行的平稳性,造成较大的误差。
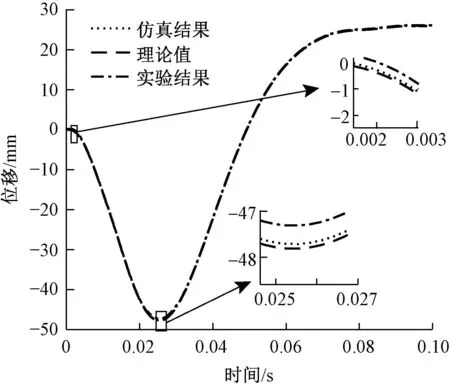
图9 理论、仿真及实验得到的分离罗拉位移
3.2 分离罗拉运动可柔性验证
为验证该系统能够实现分离罗拉的柔性运动,调整关键点的位置,推导出伺服电动机的转速,重复进行实验,得到不同有效输出长度的分离罗拉位移结果,如图10所示。
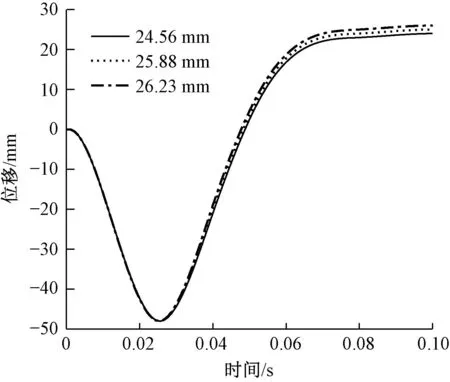
图10 不同有效输出长度的分离罗拉位移
从图10可以看出,分离罗拉位移曲线均满足“倒转-正转-停止”的规律,其有效输出长度分别为24.56、25.88及26.23 mm。这个结果说明改变伺服电动机的运动规律可得到不同的分离罗拉位移曲线,验证了分离罗拉混合驱动方式能使分离罗拉满足不同的工艺要求。
4 结 论
本文通过分段拟合方法得到分离罗拉的运动规律,利用优化设计的方法对传动系统进行优化,然后进行伺服电动机的运动规划,最后通过虚拟仿真及实验进行验证,得出如下结论。
1)对分离罗拉运动曲线进行拟合,得到的位移曲线与关键点之间误差的最大值为0.30 mm,能够满足精梳工艺要求,并且速度和加速度曲线在首末2点的值均为0,避免了刚性冲击和柔性冲击。
2)对各齿轮的齿数进行优化,使得系统中各齿轮振动加速度均方根之和比优化前减小了18.21%,达到减振的效果。
3)该驱动系统可使分离罗拉按照所设计的规律运行,克服了传统的机械驱动方式传动链长、振动剧烈等缺点,并使分离罗拉的运动具有柔性。
