新型气流牵伸通道结构模型的构建与性能分析
2023-12-24梁高翔殷俊清盛晓超吕绪山
王 青, 梁高翔, 殷俊清, 盛晓超, 吕绪山, 党 帅
(西安工程大学 机电工程学院, 陕西 西安 710048)
在纺纱过程中,需要对棉条进行多次牵伸,以将其并合、抽长、拉细,得到一定细度的纱线。目前对棉条的牵伸作用主要通过罗拉牵伸机构实现,如并条机、粗纱机和细纱机上均配备有罗拉牵伸机构,而一些新型纺纱技术如喷气涡流纺,前期也需要通过罗拉牵伸机构将棉条抽长拉细后,再进行加捻。
罗拉牵伸依靠前后罗拉的速度差实现牵伸过程,且前后罗拉速度比即为理论牵伸倍数。由于传动系统减速比的限制,前后罗拉速度比一般不会很大,限制了牵伸机构牵伸比的进一步增大。此外,罗拉牵伸过程中,始终有部分纤维处于浮游状态,且纤维间的摩擦特性是动态变化的,因此,纤维所受牵伸力大小也在不断变化,很难实现纤维的均匀排列和对棉条的均匀牵伸。为改善沿棉条长度方向上的纤维排列分布并提高成纱质量,需要保证牵伸过程中牵伸力的稳定变化。为此,不少学者开展了相关的研究工作。Ren等[1]提出并设计了纺纱机后区牵伸力检测方法和设备,利用该方法能够有效在线检测纺纱机后区牵伸力,为牵伸力的在线检测和合理选择牵伸工艺参数提供了新的途径。文献[2-4]研究了不同牵伸比条件下牵伸罗拉影响范围内的牵伸力大小及其变化,并分析其对棉条均匀度的影响。刘璐等[5]研究了在超大牵伸比条件下,不同因素对牵伸力和牵伸不匀率大小的影响。Chattopadhyay等[6]研究了牵伸力使纤维产生断裂的可能原因,并分析了其对牵伸过程产生的影响。焉瑞安等[7]基于AFIS测试仪测试了成纱牵伸过程中的纤维长度受损情况。
以上研究对纤维在罗拉牵伸方式中的受力及其对成纱质量的影响做了研究,但由于罗拉自身回转件结构及转速的限制,罗拉牵伸机构的牵伸比和牵伸效果很难继续提高,亟需寻求新的牵伸方法及对应的牵伸机构。鉴于此,本文研究了一种新型基于气流的棉条牵伸方法,并通过数值模拟仿真验证该方法的可行性。
1 气流牵伸方法的提出
气流存在黏性,会对与其相接触的物体产生摩擦力。如喷气织机利用气流对纬纱产生的摩擦牵引力带动纬纱飞越梭口,实现气流引纬;喷气纺纱、喷气涡流纺纱都利用旋转气流对纤维的摩擦力实现了加捻作用。不少学者对喷气织机引纬、喷气涡流纺气流加捻原理开展了研究工作。钱怡[8]对喷气织机纬纱入射流场进行了数值模拟和参数优化;Kim等[9]对引纬过程中辅助喷嘴喷射气流特性进行了数值模拟;Wu等[10]分析了引纬起始阶段的气流特性和纱线运动规律;文献[11-12]分别研究了引纬过程中纬纱、纤维束的运动情况。邹专勇等[13]分析了不同结构参数下旋转气流对纱线加捻特性的影响;郑凌晨[14]研究了喷气涡流纺流场特性,且探索研究了纤维建模方法;陈洪立等[15]研究了导引针和导引部件对喷气涡流纺流场的影响情况;尚珊珊等[16]通过数值模拟分析了喷气涡流纺流场中的旋转气流,以及纱线运动规律;陈美玉等[17]研究了缠绕和加捻对喷气涡流纺纱力学性能的影响 。以上研究均直接或间接表明,气流可以实现对纤维(束)或纱线的运动控制。
此外,根据拉瓦尔喷管(见图1)原理:当气流为亚音速,气流在管道中运动时,截面小处流速大,截面大处流速小,即气流流经收缩段时会不断加速。
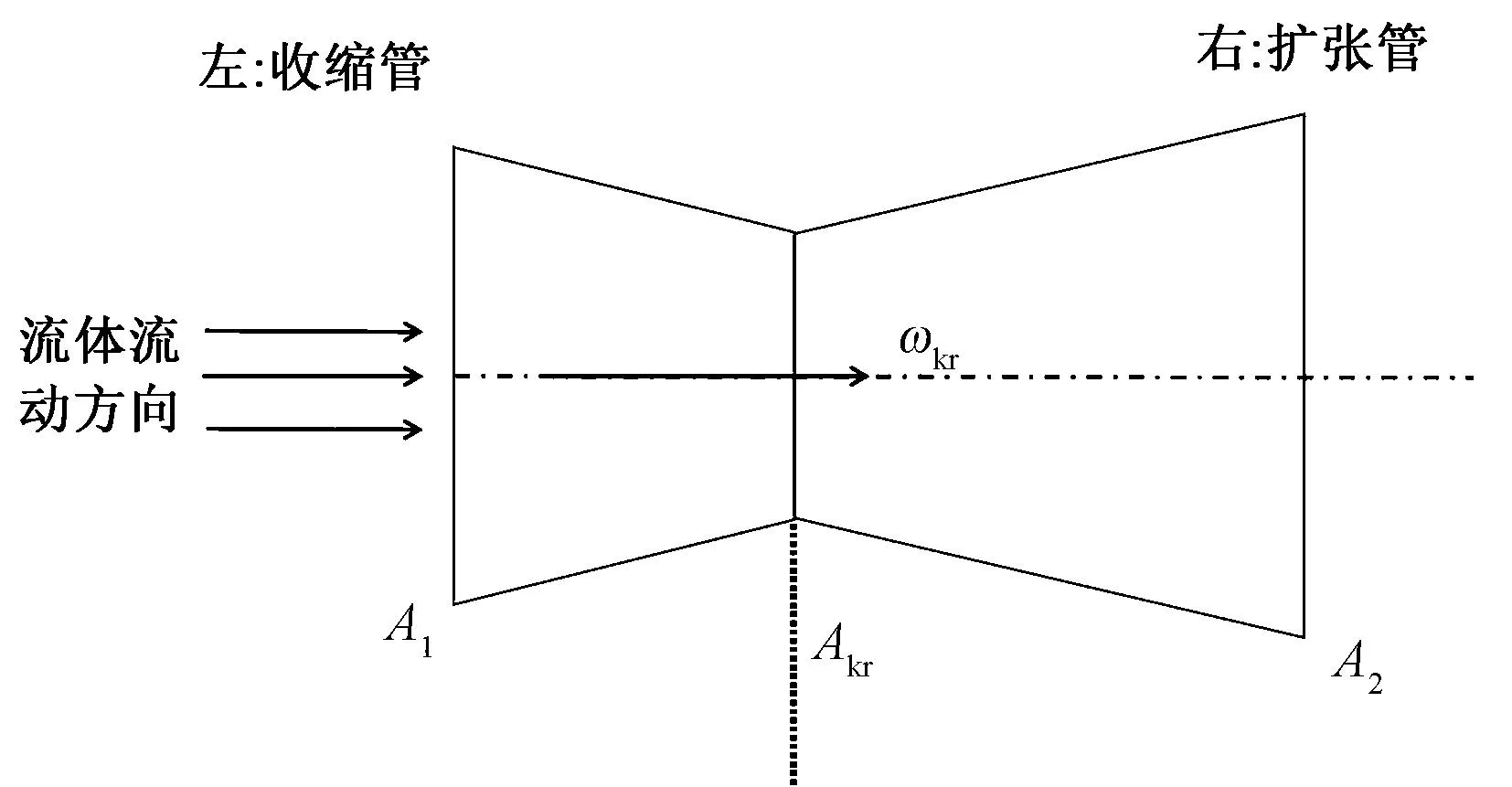
A1为喷管入口截面积;Akr为喷管喉部截面积;A2为喷管出口截面积;ωkr为喷管喉部流速。
综合气流上述2个方面的特点,当亚音速气流和纤维同时在收缩型管道中流动时,可以推断出:1)由于气流对纤维的摩擦牵引力,会带动纤维一起向前运动;2)随着管道截面的收缩,气流速度不断增大,纤维速度也不断增加;3)考虑到气流和壁面之间的黏性效应,在同一截面不同位置处,气流速度并不相同,则对纤维的摩擦牵引力大小也不相同,带动纤维运动的速度也不相同。综合这3个方面的特点,纤维在管道中不同位置处运动速度各不相同,从而实现纤维的重新分布。同时考虑单位时间内输入管道中的纤维质量和单位时间内输出纤维的质量应该相等,而输出端纤维速度大幅增加,因此,输出端纤维变细,即实现了牵伸效果。
综上分析,本文提出一种在收缩型管道内通过气流对棉条进行牵伸的方法,即气流牵伸方法。该方法在文献[18]中有提及,但只进行了简单的流场分析,没有考虑纤维在流场中的具体运动,以及多根纤维之间的相对运动过程,不能充分证明其方法的可行性。本文根据牵伸比的要求,重新推导气流牵伸通道的结构、尺寸等参数,并充分考虑纤维和流场之间的双向耦合影响,论证该方法的可行性,为气流牵伸方法的工程化应用提供一定的理论参考。
2 气流牵伸通道建模
考虑喷气涡流纺的气流纺纱特点,本文假设从气流牵伸通道出来的棉条直接进入喷气涡流纺纱机的加捻通道。下文中的气流牵伸通道参数分析计算均以此假设为前提。
2.1 牵伸通道结构和工艺参数分析
根据上述假设,牵伸通道的出口速度应与喷气涡流纺加捻腔的引纱速度相匹配。喷气涡流纺的引纱速度一般达400~450 m/s,因此,牵伸通道出口气流速度取Vout为420 m/s。同时,参考粗纱和细纱工艺的总牵伸倍数,取气流牵伸通道的牵伸倍数为140。
牵伸倍数一般为牵伸前后棉条的细度之比,此处假设棉条中的纤维均匀填充牵伸通道,则输入端和输出端棉条细度之比近似为牵伸通道入口截面积和出口截面积之比。牵伸通道出口尺寸大小参考喷气涡流纺纱机加捻部分的空心锭子入口结构尺寸,设为1 mm,则可根据牵伸倍数计算得到牵伸通道入口直径约为12 mm。进而,根据质量守恒定理(即式(1)),计算得到通道入口气流速度Vin为3 m/s,通道长度设为50 mm[18]。通道入口处压强设为大气压,大小为101 325 Pa,根据喷气涡流纺喷嘴内流场仿真,得到牵伸通道出口处压力值为-0.01 MPa。
Qin=Qout=vs
(1)
式中:Qin为单位时间流入通道的气体量,m3/s;Qout为单位时间流出通道的气体量,m3/s;v为气流速度,m/s;s为通道截面积,m2。
2.2 纤维在气流中的受力分析
纤维在气流中运动时,会在平行于气流运动的表面上产生黏滞力,即相当于纤维在罗拉牵伸方式中所受到的摩擦力,如图2示出。黏滞力Fs的大小和流体的密度、温度、速度等参数有关,其大小可按下式计算:
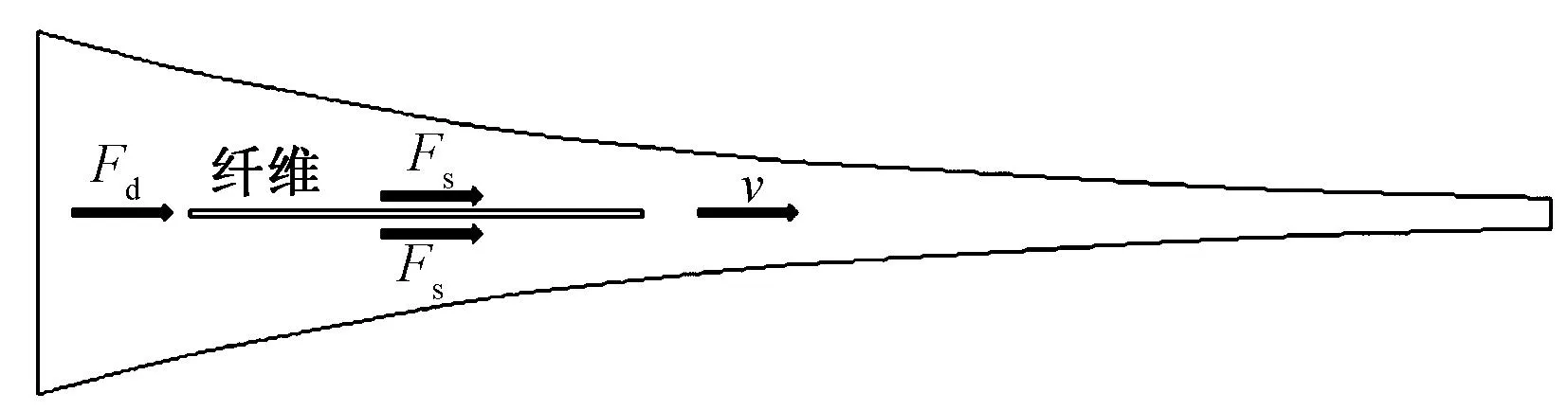
图2 平行伸直纤维在气流中的受力
Fs=-6πηrv
(2)
式中:η为空气黏性系数,值为1.983×10-5Pa/s;r为纤维半径,m。
带动纤维在牵伸通道中运动的力除作用在其表面的黏滞力Fs外,还有一部分是作用在纤维头端的动压力Fd,假设纤维头端为平面,则动压力Fd的大小为
(3)
式中:ρ为气流密度,kg/m3;S为纤维头端平面面积,m2。
综上分析,纤维在气流中受到的总力F为
(4)
2.3 牵伸通道参数设计
已知牵伸通道出入口直径和通道长度,根据式(1)和式(4)可以确定纤维在牵伸通道内受到的总力F与通道截面积s,进而得到与通道半径之间的关系。将该关系式与罗拉牵伸方式中的理想摩擦力界曲线拟合得到通道长度和通道半径之间的关系,如图3示出。图3中横坐标起点为牵伸通道入口截面中心。根据图3的关系曲线,即可得到气流牵伸通道的结构模型,如图4所示。
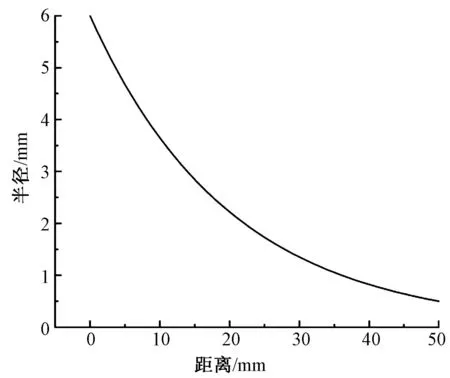
图3 通道半径与长度关系曲线

图4 牵伸通道模型示意图
2.4 牵伸通道模型流场特性分析
为验证上述牵伸通道模型设计的合理性,使用Fluent软件对牵伸通道内流场进行数值模拟,且暂不考虑纤维的影响。选取Realizablek-ε湍流求解模型,设置参考压强为0 Pa。气流入口和出口分别设置为压力入口和压力出口边界条件,其值大小参见2.1节,数值模拟得到流场参数曲线如图5~7所示。

图5 通道中心线速度分布图
由图5牵伸通道中心线附近的速度分布曲线可见,随着牵伸通道的不断收缩,气流速度持续增大,特别是靠近出口位置处气流速度迅速增大。牵伸通道出口最大气流速度约为426 m/s,根据牵伸通道入口速度3 m/s计算,牵伸比达142,满足牵伸比140的要求。由图6沿着牵伸通道中心线处的气流静压分布曲线可见,随着气流速度的增大,气流静压不断减少。图7为沿着牵伸通道的气流速度等值线,反映了气流在牵伸通道加速过程中的具体速度分布,其分布和理论分析相吻合。3个曲线图均说明本文设计的牵伸通道理论上可以实现牵伸比为140的牵伸效果。

图6 通道中心线压力分布图
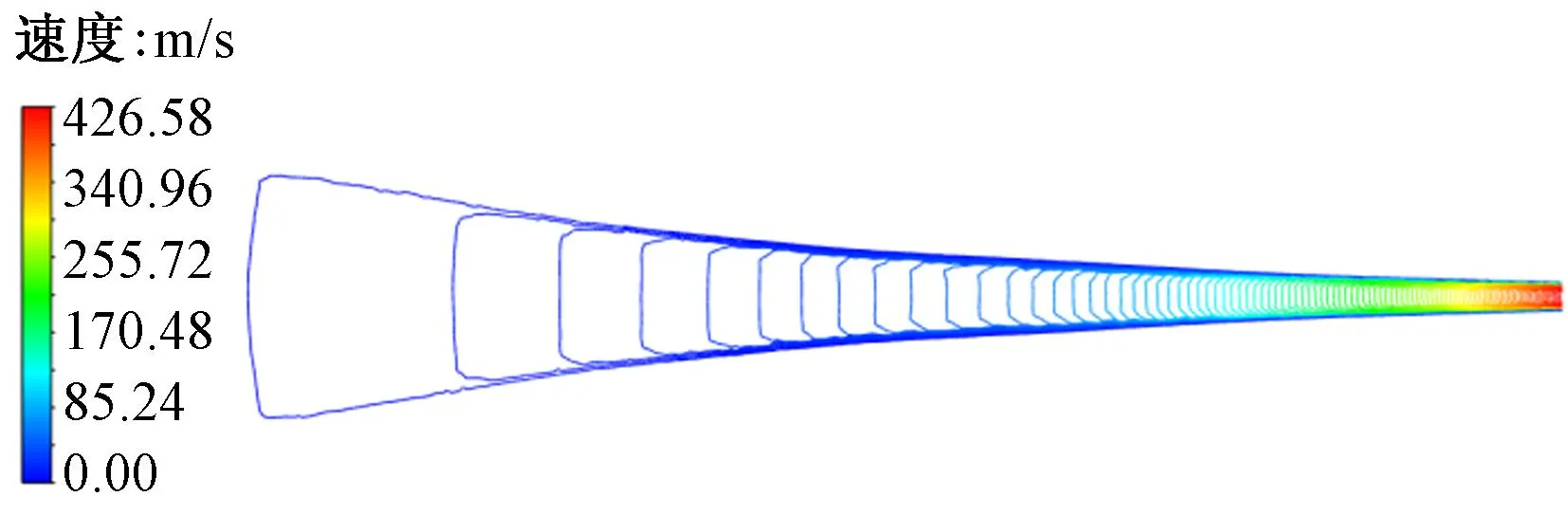
图7 速度等值线梯度图
3 纤维-流场双向耦合影响分析
前文数值模拟了气流牵伸通道的流场特性,但没有考虑纤维和流场的相互影响,因此,本节将分别考虑单根伸直纤维、2根平行伸直纤维,以及单根前弯钩纤维在流场中的具体运动情况,进一步验证本文所提方法的可行性。
3.1 纤维建模
纤维是长径比大的细长弹性体,因此,采用二维柔性弹性纤维模型。图8示出不同状态下的纤维模型。在没有外力的情况下,伸直纤维被描述为长径比大的矩形。矩形的长度方向表示纤维的长度方向,宽度方向表示纤维的径向。图8(a)为无外力作用时的纤维模型和纤维离散化模型,对纤维进行四边形网格划分,每个小四边形网格为一个子单元。纤维受外力作用而产生变形,在分析时假设力的作用点都在节点,如图8(b)、(c)所示。
3.2 纤维与气流的耦合控制
流固耦合数值方法有任意拉格朗日-欧拉法(ALE)、格子玻尔兹曼法(LBM)、浸入边界法(IBM)和有限差分法(FDM)等。ALE方法中流体区域的节点可以根据固体边界的变化产生相对位移,可用于解决纤维在流场内的运动和大变形问题,计算的结果更能反映实际情况,因此,采用ALE方法研究牵伸通道中气流与纤维的耦合问题。气流和纤维之间需在每个迭代步间传递力与位移数据,满足动力学与运动学条件[19]:
(5)
式中:df和ds分别为纤维和气流在接触处的位移,mm;σf和σs分别为纤维和气流在接触处的应力,Pa;n为接触处的法向量。
3.3 固体间接触控制
纤维在流场内的运动形式比较复杂且自身变形较大,纤维与通道内壁、纤维和纤维之间会发生碰撞、摩擦等接触行为,若不限制该接触运动形式,纤维和壁面、纤维和纤维之间会发生相互侵入的现象,进而使得Fluent求解器在计算时会因出现负体积网格而导致计算发生错误。为解决触碰问题,需要在纤维和壁面、纤维和纤维之间添加动力学限制条件。由于这2种碰撞问题本质上是一个问题,因此,接触控制分析用固体A和固体B来指代2个物体。
当固体A与固体B间发生接触时,二者间间隙距离为零。从接触时刻起,固体A与固体B之间产生接触力来防止固体间相互侵入。固体A与固体B间的间隙距离函数[20]可定义为
g(xA,t)=min‖xA-xB‖
(6)
式中:xA为固体A与固体B发生接触的面上一点;xB为固体B与固体A发生接触的面上一点。则有:
(7)
式中:yB为固体B与固体A发生接触的面上距离xA最近的一点;nB为相应的固体B上外向单位法向量;tc为2个固体界面间的接触力;λ为法向接触力。
则上述接触系统满足的法向条件为:g≥0,λ≥0,gλ=0。表明当g≥0时,固体A与固体B间未触碰,故λ=0;当g=0时,固体A与固体B间存在触碰作用,λ为大于零的有限值。
此外,为简化模型计算,暂不考虑纤维和壁面、纤维和纤维间的摩擦作用。
3.4 计算区域的建立及网格划分
图9为单根伸直纤维与流场耦合模型的计算区域示意图。将纤维置于牵伸通道内流场中,其长度为15 mm,尾端距离通道入口处5 mm作为纤维的初始位置。
对流体域和纤维区域分别进行网格划分。考虑到纤维在流场内的运动形式比较复杂,为方便网格更新,对流体域采用三角形网格进行网格划分,并对纤维与气流交界处区域进行网格加密,以提高网格质量,进而提高计算精确度。网格划分和网格加密图如图10示出。

图10 流固耦合模型网格划分
3.5 材料属性设置
纤维模型采用长绒棉,流体为理想空气,其材料属性如表1所示。纤维在牵伸过程中横截面积和直径的变化较小,因此,在计算中将纤维泊松比设置为0[21]。

表1 纤维与流体的材料属性参数
3.6 求解方式及边界条件设置
基于ANSYS Workbench软件搭建流固耦合求解平台,应用Fluent模块对流体域进行求解,压力入口和压力出口边界条件设置参见2.1节。采用Transient Structural模块对纤维结构进行瞬态计算,根据表1所示设置纤维参数。使用System Coupling模块实现流场和纤维计算数据间的交换。该数值模拟方法在文献[19-20]中均被用到,且在文献[20]中通过实验证实了该方法的有效性。流固耦合仿真流程图如图11所示。
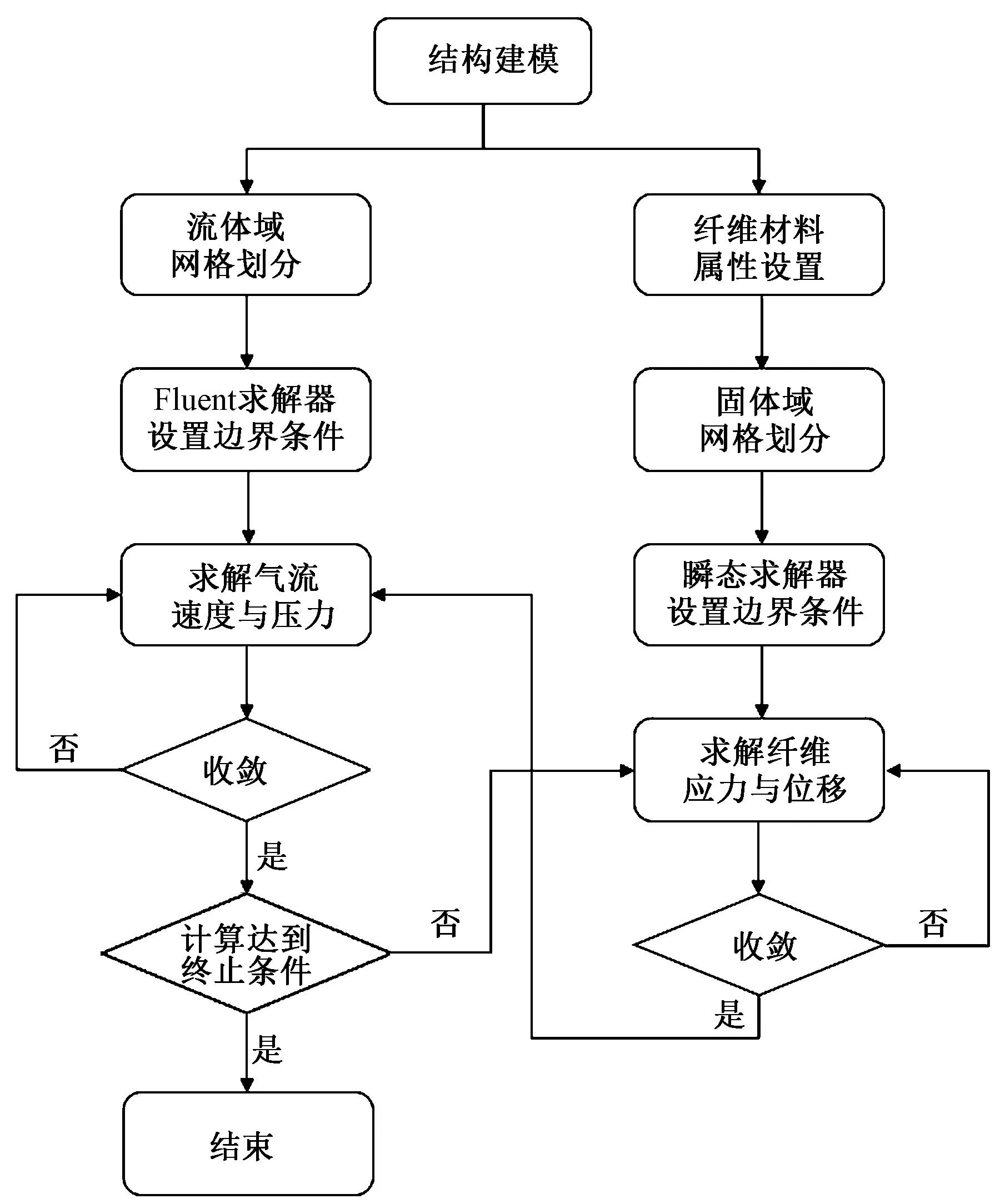
图11 流固耦合仿真流程图
4 纤维-流场双向耦合影响结果分析
采用上述流固耦合求解平台,分别实现单根伸直纤维、双根伸直纤维和单根弯钩纤维的流场耦合影响的二维模拟研究,结果如图12~14所示。
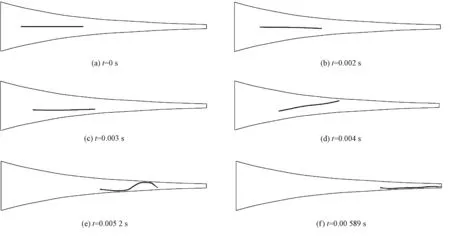
图12 单根直线型纤维模型运动规律
分析图12可知:1)根据拉瓦尔喷管原理和质量守恒方程,气流在牵伸通道内的速度不断增大,纤维的运动速度随气流速度的增大而增大;2)受横向气流速度影响,纤维在通道内的运动存在一定的上下摆动和波动。纤维处于通道入口段时,气流速度较小,横向气流速度分量也小,导致纤维波动较小,整体随着气流上下摆动式前进;当纤维运动至通道中后段时,气流速度增大,横向气流速度也随之增大,使得纤维波动幅度增大;3)气流在牵伸通道中流动的速度梯度很大,因此,纤维头端的气流速度要高于纤维尾端,其结果是纤维伸直平行流出牵伸通道,即实现拉直纤维的目的。
分析图13可知:1)2根伸直平行纤维在牵伸通道中运动时,纤维之间会相互靠拢并发生接触和摩擦。受横向气流影响,纤维在向前运动过程中存在一定波动,但整体波动较小;2)从0.003 s左右起,纤维之间开始出现位移差,0.005 s后2根纤维头端的距离偏移已较为明显,且随着时间的推移,纤维间位移差越来越大。较快的纤维运动到通道出口处时,2根纤维间的偏移已接近半根纤维的长度,且纤维分离情况良好,证明了气流牵伸通道拥有较好的纤维变速点分布,能够有效地提高成纱条干均匀度;3)2根纤维在流场中的运动规律可以推广到多根纤维,最终结果是实现纤维的重新分布排列,达到牵伸的目的。
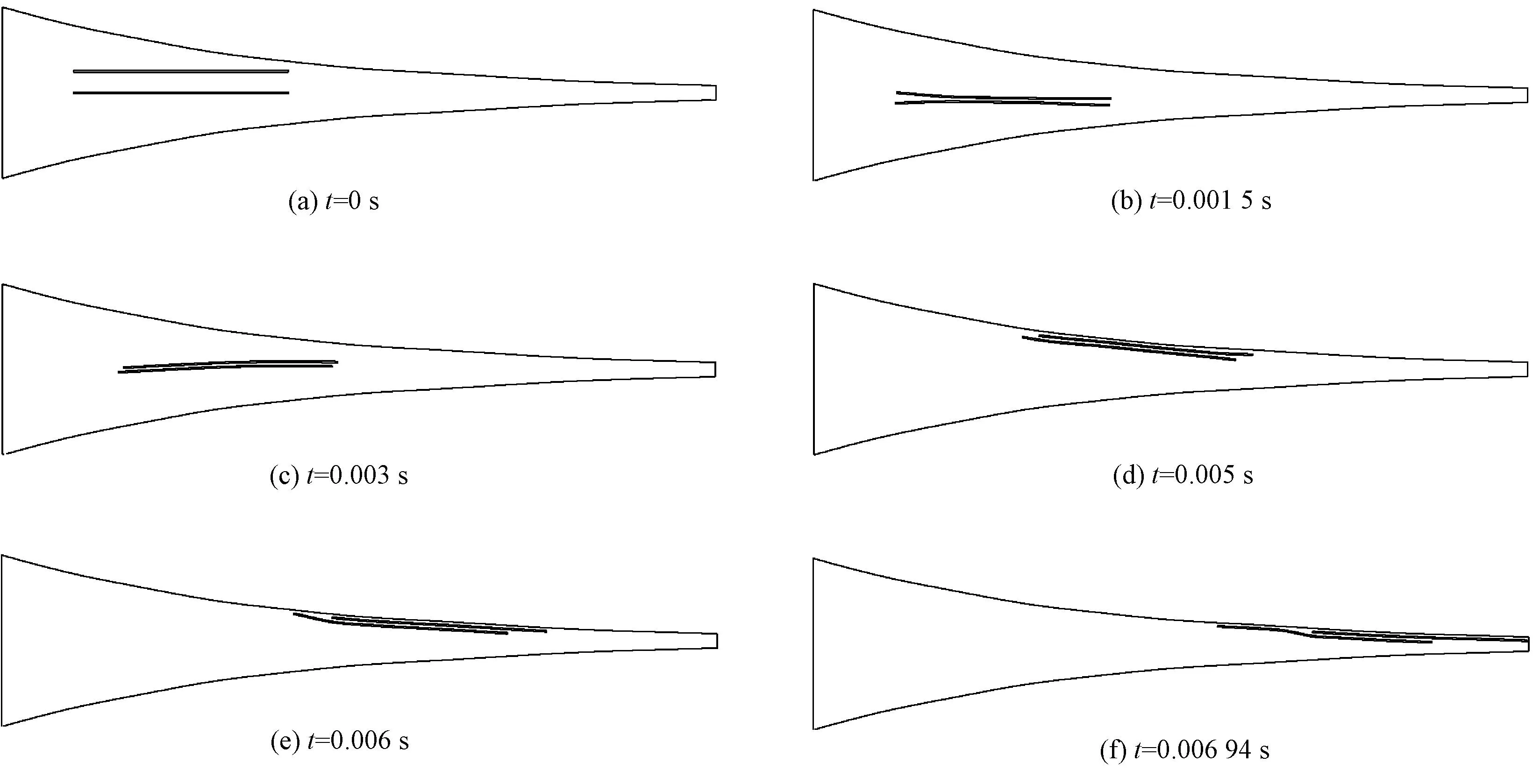
图13 双根直线型纤维模型运动规律
分析图14可知:1)在流场中,弯钩纤维的迎风面积更大,受气流轴向分力的影响更为显著,因此,与伸直纤维相比,弯钩纤维在牵伸通道内的运动速度更快,运动总时长大幅减少;2)弯钩纤维在牵伸通道向前运动过程中,由于气流摩擦力的影响,弯钩逐渐伸直平行;3)随着弯钩纤维逐渐伸直,其迎风面积逐渐减小,故纤维运动加速度变小,使得纤维在牵伸通道后半段加速性减慢;4)据此还可推断,当弯钩纤维和伸直纤维同时在牵伸通道中运动时,会因受到牵引力大小不同而相互前后错开运动,即实现纤维的重新分布排列。

图14 单根弯钩型纤维模型运动规律
此外,分析图12~14还可发现,3种情况下,纤维都出现贴着牵伸通道内壁面运动的现象,分析原因在于:1)由于附面层效应,贴近壁面的气流速度会小于牵伸通道中心的速度,且距离牵伸通道中心越远,气流速度越低,因此,纤维在这种速度梯度影响下逐渐向壁面方向靠近;2)纤维在牵伸通道中一方面向前运动,同时向壁面方向靠近,而牵伸通道尺寸较小,使得纤维还未流出通道就已经接触到壁面,出现紧贴着壁面运动的现象。
5 结 论
根据空气黏性特点,同时参考喷气织机和喷气涡流纺纱特性,提出了一种基于气流的棉条牵伸方法。建立了气流牵伸通道结构模型,以及纤维与气流的双向耦合分析模型,通过分别模拟单根伸直纤维、双根伸直纤维和单根弯钩纤维在流场中的运动,验证了所提方法的可行性,得出如下结论。
1)伸直平行纤维在牵伸通道中向前运动时会产生波动,但当其到达牵伸通道出口附近时,再次伸直平行流出牵伸通道,且纤维一直在加速运动。
2)当2根伸直纤维在牵伸通道中前进时,由于不同位置的气流速度不同,使得2根纤维相互错开前进,该现象说明多根纤维在牵伸通道中向前运动时,纤维会重新分布排列。
3)弯钩纤维在牵伸通道中运动时,由于迎风面积大,气流对其的牵引力大,因此,弯钩纤维的运动速度相比于伸直平行纤维会更快,在牵伸通道中运行时间更短。据此可推断,当弯钩纤维和伸直纤维同时在牵伸通道中运动时,它们会因速度不同而前后错开,即实现纤维的重新分布排列。
4)弯钩纤维在运动过程中会由于气流牵引力而逐渐伸直,即实现与罗拉牵伸类似的拉直纤维的目标。
