Dynamic Event-Triggered Control of Continuous-Time Systems With Random Impulses

Meng Yao and Guoliang Wei

Abstract—In this paper, the networked control problem under event-triggered schemes is considered for a class of continuoustime linear systems with random impulses.In order to save communication costs and lighten communication burden, a dynamic event-triggered scheme whose threshold parameter is dynamically adjusted by a given evolutionary rule, is employed to manage the transmission of data packets.Moreover, the evolution of the threshold parameter only depends on the sampled measurement output, and hence eliminates the influence of impulsive signals on the event-triggered mechanism.Then, with the help of a stochastic analysis method and Lyapunov theory, the existence conditions of desired controller gains are received to guarantee the corresponding input-to-state stability of the addressed system.Furthermore, according to the semi-definite programming property, the desired controller gains are calculated by resorting to the solution of three linear matrix inequalities.In the end, the feasibility and validity of the developed control strategy are verified by a simulation example.

I.INTRODUCTION

OVER the past few years, impulsive systems have received increasing attention, mainly because they have the capability of characterizing dynamical behavior, which could be interrupted by instantaneous state jumps.Such systems have a wide range of applications in chaotic secure communication[1], robotics [2], automatic braking [3], aerospace [4], etc.Generally, they consist of three parts: the continuous-time evolution between the impulsive instants, the discrete-time impulsive dynamics, and the sequence set of strictly increasing impulsive instants [5], [6].Up until now, plenty of results have been reported on such systems (see [7]–[12] and references therein).For example, sufficient conditions have been developed in [7] to ensure the exponential stability of nonlinear impulsive systems.Meanwhile, the corresponding filtering problem has been investigated in [8]–[12] for discretetime linear systems with impulsive effects.

The concept of input-to-state stability (ISS) is originally introduced by Sontag [13] to describe the influence of external inputs on practical engineering systems.The ISS property implies that the system is exponentially stable for the disturbance-free case and bounded stable under bounded inputs.Moreover, such a property is also helpful in the robustness analysis and controller design [14], [15].It is worth mentioning that integral input-to-state stability (iISS) is a weaker concept and can be regarded as a natural extension of ISS.

In recent years, the ISS property is one of the hottest topics in the control community due to its powerful capabilities and wide applications in characterizing the effects of exogenous disturbances on systems.As a result, a large number of meaningful results have been reported to cope with the problems of ISS for engineering systems under external noises, e.g.,[16]–[19].Among them, ISS problems of impulsive systems have also derived considerable results.For instance, the ISS property of impulsive systems was first investigated in [20]with the help of the average impulsive interval approach.By resorting to the comparison principle, sufficient conditions have been developed in [21] to ensure the ISS of impulsive stochastic systems.Recently, the corresponding results on ISS have been applied to nonlinear systems with delayed impulses[22].In this paper, different from the aforementioned results,we focus on the ISS issue of networked control systems with random impulses.

Another research topic is to study the networked control problem of impulsive systems under the communication protocol.With the digital revolution of communication technologies, a large number of engineering systems employ networks to contact the system components instead of traditional pointto-point connection [23]–[28].Such a special form has led to the merits of easy maintenance, remote control, and high expansibility.However, it also results in unexpected phenomena, such as network-induced time-delays and malicious attacks.Moreover, because of limited network bandwidth, network jamming would occur which, if not well handled, could degrade system performance [29]–[33].Hence, it is necessary to utilize communication protocols to manage data transmission with the purpose of reducing network congestion.

As we all know, compared with the time-driven scheme, the event-triggered mechanism (ETM) can effectively improve the utilization of network resources in networked systems and guarantees certain system performance.Under the ETM, the sampled data will not be transmitted through the communication network unless the triggered condition is satisfied[34]–[36].According to different triggered conditions, the most existing ETMs will be roughly divided into two categories: the static case and the dynamic case.The triggering rule of the static event-triggered mechanism (SETM) is predefined and fixed.Nevertheless, the dynamic event-triggered mechanism (DETM) adopts a dynamically adjustable parameter for the triggering rule.Moreover, DETM could economize more network resources and improve the efficiency of data transmission.To this day, there are plenty of significant articles that have been reported on systems under ETMs (see[37]–[40] and references therein).However, for the continuous-time systems with random impulses, the networked control issue under DETM has been neglected mainly due to the difficulties in establishing suitable triggering rules for such a kind of system.

Motivated by the above discussions, in this paper, we aim to design the DETM-based controller such that the continuoustime systems subject to random impulses and bounded noises can achieve ISS.The investigated topic presents significant challenges, including but not limited to: 1) How to set up a suitable mathematical model to describe the dynamic behavior of the impulsive system under DETM? 2) How to establish appropriate mathematical methods to analyze ISS of such impulsive systems? 3) How to design the expected controller gain to efficiently handle the bounded noises and random impulsive signals?

In this paper, our objective is to conquer the above challenges, where the primary contributions can be seen in the next three aspects: 1) A DETM-based control algorithm is provided for impulsive systems subject to random impulsive signals.By resorting to the artificial time-delayed approach,the addressed system can be viewed as an impulsive timedelayed one; 2) With the help of stochastic analysis approaches and the developed Lyapunov-Krasovskii functional, sufficient conditions are obtained to ensure the ISS property; and 3) According to the acquired sufficient conditions, the expected controller gain is calculated by employing the semidefinite programming approach.

The rest of this paper is constructed as follows.Section II formulates the DETM-based networked control problem of continuous-time systems under random impulses.The ISS problem of the impulsive system under random impulses and DETM are detailed in Section III.The case study is presented in Section IV to verify the feasibility and validity of the proposed control strategy, followed by the conclusion in Section V.

Notations: Throughout this paper, E{·} denotes the mathematical expectation.N represents the positive integer set.The diag{···} represents a block-diagonal matrix.Let K be a class of continuous strictly increasing functionsf:R+→R+withf(0)=0.Moreover,fis said to be a K∞-function if it belongs to K-function and satisfiesf(s)→∞ ass→∞.A functiong:R+×R+→R+isaKL-function if,foreachfixedt∈R+,g(·,t) is a K-function,andforeachfixeds∈R+,g(s,·)is decreasing andg(s,t)→0 ast→∞.

II.PROBLEM FORMULATION

A. System Description

In this paper, the considered impulsive system is presented as follows:

Assumption 1: There are several different kinds of stochastic impulsive sequences, whose strength takes values from the set Γ ={µi,i=1,2,...,δ} with m axi∈Γ{E{µi}}<∞.

In this paper, the system states are sampled at instants{sh,h∈N} , and the sampling instants satisfysh+1-sh=TwithT>0is the constant sampling period.

B. DETM

In the following, we shall introduce the DETM.Before further proceeding, denoteskn=tk+nT(n=1,2,...,tk+1-1),wheretkis the triggered instant.Then, the dynamic event-triggered scheme is shown as follows:

with the initial condition η (t)=η0>0 and β >0.

Note that the above mentioned triggered condition (2) can be translated into

Whenθgoes to +∞, we can obtain 1 /θ=0, which implies that SETM is a special form of the DETM.

In what follows, according to the artificial time-delayed approach, the event-triggered impulsive system will be reformulated as an impulsive system with time-delay.Under this setting, we can directly analyze its networked control problem under the DETM.

For the convenience of narration, we denote H =[tk,tk+1] as the interval between two triggered instants.Then, it could be divided as

From the above discussions, the actual input of the addressed system is

According to (6), a dynamic of networked system under both the DETM and random impulses is derived as follows:

For the system (7), the initial value ofx(t) is supplemented asx(t)=ϕ(t),t∈[-T,0], where ϕ(t) is the initial condition ofx(t).

For further discussions, the definitions of ISS and average impulsive interval are given as follows.

Definition 1: The closed-loop system (7) is said to be stabilized to

1) ISS by controller (6), if there exist functions κ ∈KL and χ ∈K∞such that

2) iISS by controller (6), if there exist functions κ ∈KL and χ ∈K∞such that

Definition 2[41]: LetNi(t,s) be the number of thei-th impulsive signals.If

where Ti>0 andN0≥0, then TiandN0are respectively named the average impulsive interval and the elasticity number.

Our main objective is to develop a DETM-based controller for the closed-loop system (7) with the triggering rule (2) such that the addressed system subject tow(t) is ISS and iISS.

Remark 1: The parameter η(t) in the DETM is positive under the condition θ ≥(eβh-1).The explicit solution of (3)is shown as

Considering the DETM (2) derives

Then, we get that, for allt∈[skn,skn+1),

Remark 2: Compared with the widely adopted SETM, the DETM is capable of further reducing the communication cost and lowering the update frequency of controllers.The main difference lies in the triggering rule.Specifically, compared with SETM with the fixed parameters, there is a dynamical parameter in the DETM, which plays an important role in excluding the Zeno behavior.Under this kind of communication protocol, the challenges are summarized as follows: 1)How to analyze the effect of the DETM on impulsive systems? 2) How to establish a unified design framework taking both the control scheme and the DETM into consideration? 3)How to develop a suitable DETM to adapt to the evolution of addressed systems?

III.MAIN RESULTS

In this section, we consider the ISS and iISS problems of networked impulsive systems under the DETM.The impulses are assumed to have stochastic impulsive strengths.First, sufficient conditions will be presented to ensure the ISS and iISS of the addressed system.Subsequently, the controller gains are obtained based on these developed sufficient conditions as well as semi-definite programming approaches.

A. ISS and iISS Analysis of Networked Impulsive Systems

In what follows, we shall introduce two conditions to check that the addressed system (7) can achieve ISS or iISS.

Theorem 1: Under Assumption 1, for given constantsα>0 andT>0 , if there exist positive constants ϵ,θ, and β ∈[2α,∞), positive-definite matricesP,SandS1, and matrixGsuch that

where

Then, by controller (6), the addressed system (7) is stabilized to ISS.

Proof: First of all, choose a Lyapunov functionalV(t) with the following form:

where

The infinite-dimensional operator L of Lyapunov functionV(t)is represented as

DifferentiatingV(t) along the system (7), we have

将自来水+普通石英砂5%(按粒径分组)混合后放置于圆形漏斗状水槽中，开泵使固液两相流循环流动运行2～3小时，取出贴片清洗干燥后再次称重，计算金属贴片的冲蚀速率和失重率。根据石英砂粒径将试验分为四组，另外一组为对照试验组。主要试验参数见表1。表中目数即筛分粒度，表示颗粒可以通过筛网的筛孔尺寸，以宽25.4mm筛网内的筛孔数表示。循环管路内径为2.5mm。

In what follows, we will handle the integral term in the above equation, which is difficult to be written in a linear matrix inequality.Employing the representation

and the Jensen’s inequality, we arrive at

whereψ=col[x(t)-x(t-τ(t)),x(t-τ(t))-x(t-T)], and Ω given in Theorem 1.Then, settingh¯=[x(t),x(t-τ(t)),x(t-T),e(skn),w(t)], one has

It follows from (17) that:

Subsequently, multiplying both side of (18) withe-2αt, we arrive at

Integrating both side of (19) from ξktot, one can have that for ∀t∈[ξk,ξk+1),

In what follows, we are ready to consider the impulsive effects.Whent=ξk, in view of (12), one has

For the convenience, denote the impulsive instants as ξ1, ξ2,..., ξl, and define the symbol Fl=σ(λr(ξ1),...,λr(ξl)),∀l∈Z.Note that the {λl}l∈Γare independent of each other.Hence, according to (21), we can derive that

Then, combining (20) and (22) implies that

where ϑi=E{λr(ξi)}.Recalling Definition 2, one obtains

Bearing in mind the boundedness of noises (i.e.,//w(t)//[0,+∞)≤ϖ), we obtain that

On the other hand, noticing that

for some scalar κ >0, one has

Substituting (25) and (26) into (24) derives that

Denote

and

It is not difficult to find that the requirement of Definition 1 is satisfied.■

In what follows, we will investigate the iISS issue for the considered system.

Theorem 2: Under Assumption 1, for given constantsα>0 andT>0 , if there exist positive constants ϵ ,θandβ ∈[2α,∞), positive-definite matricesP,SandS1, and matrixGsuch that conditions (8)–(10) are satisfied.Then, by controller (6),the addressed system (7) is stabilized to iISS.

Proof: We start by recalling (24) that

Considering the Lyapunov functional, one derives

Subsequently, it follows from (28) and (29) that:

According to the initial condition, it is not difficult to find that

Therefore, we can claim that the addressed system (7) is stabilized to iISS.■

Remark 3: For ∀i∈Γ, if the expectation of the impulsive intensity 0 <ϑi<1, then thei-th kind of stochastic impulse is a stabilizing one.On the other hand, if the expectation ϑi>1,then thei-th kind of stochastic impulse is a destabilizing one.It should be pointed out that the discussed system could not be stable if the number of stochastic impulses that occur with intensity 0 <ϑi<1 is infinite in a limited time interval.

Remark 4: Compared with the existing results involving ISS problems of impulsive systems, our results exhibit the following distinguishing features: 1) The addressed dynamic eventtriggered-based ISS problem is new and represents one of the first few attempts to deal with impulsive systems subject to bounded noises; 2) The proposed DETM only depends on the sampled output, and hence eliminates the impulsive effects on the triggering rule; and 3) The Lyapunov functional and some properties of stochastic processes are utilized to study the addressed problem.

Remark 5: In order to analyze the effects of communication protocols on system performance, a dynamic parameterη(t)has been added in the Lyapunov functional.However, the parameter η(t) brings difficulties to the derivation of sufficient conditions of ISS performance.In addition, the DETM also brings effects on solving the desired controller gains since the parameters Ψ andβshould be considered.

B. Controller Gain Design

In the preceding discussions, a series of sufficient conditions have been got to guarantee the ISS and iISS performance of systems with random impulses.Based on the above sufficient conditions, we are now ready to set up sufficient conditions to calculate the controller gain, which is important for practical application.

For the convenience of presentation, we define the following matrices:

withX=P-1.

Theorem 3: Under Assumption 1, for given positive constantsα,T, ϵ ,θand β ∈[2α,+∞), if there exist positive-definite matricesX,Sˆ ,Sˆ1and Ψˆ , and matrixGˆ such that,

where

Then, by controller (6), the addressed system (7) is stabilized to ISS (iISS).Furthermore, the controller gain matrix is given byK=YX-1.

Proof: DefineJ=diag{X,X,X,X,I,S-11}.Then, multiplying both sides of (10) byJand its transpose, we derive that

which guarantees Φ <0.It is noticed that -is a nonlinear term and the above matrix inequality can not be directly solved by the MATLAB linear matrix inequality (LMI) toolbox.As such, we need to transform this nonlinear term into a one that is linear.Consider the following inequality:

Then, it follows from (36) that:

It is obvious that nonlinear termcan be replaced by linear termin (34).And, the expected controller gainKcould be obtained by resorting to the solutions of the linear matrix inequalities (32)–(34).■

IV.CASE STUDY

In this section, the effectiveness and availability of the established control strategy will be verified by a simulation example.Consider an impulsive dynamic with the following parameters:

The bounded noise is chosen as

Let the stochastic strength µ1satisfy the uniform distributionU(-0.4,0.6) and µ2obey the distribution given in Table I.Then, we obtain that ϑ1=1.21 and ϑ2=1.047.

PROBABILITYT DAIBSTLREIB IU TIONS OF µ2

According to Theorem 1, the impulsive interval satisfies

In this simulation, we denote T1=0.8, T2=0.8,T=0.1,and α=1.566.Subsequently, by resorting to the solutions of the linear matrix inequalities (33) and (34), the DETM-based controller gainKis obtained as

For the purpose of simulation, the initial conditions and event-triggered parameters are chosen asx(t0)=[-0.1,0.5,-0.1], ϵ=0.1, θ=1 and η(t0)=1.Moreover, the simulation results are presented in Figs.1–5.The state trajectories of the open-loop system are depicted in Fig.1, and obviously are apparently unstable.After implementing the proposed control strategy, the state trajectories of the closed-loop system are plotted in Fig.2, which clearly shows the feasibility of the proposed method.The event-triggered instants and the evolution of η (t) can be seen in Fig.3.

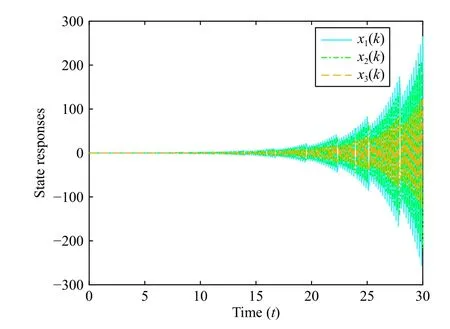
Fig.1.State trajectories of the open-loop system.

Fig.2.State trajectories of the closed-loop system under DETM.

In order to examine the advantage of the DETM, we shall provide a simulation comparison between DETM and SETM.Fig.4 plots the evolution of the close-loop system under SETM with controller gain

Moreover, the initial states are chosen asx(t0)=[-0.1,0.5,-0.1].In Fig.5, we can conclude that the triggering rate of DETM is much lower than one of SETM.In fact, the triggering numbers of DETM and SETM are 98 and 129, respectively.On the other hand, by comparing Fig.2 with Fig.4, we find that the states of SETM can more quickly achieve bounded stability.

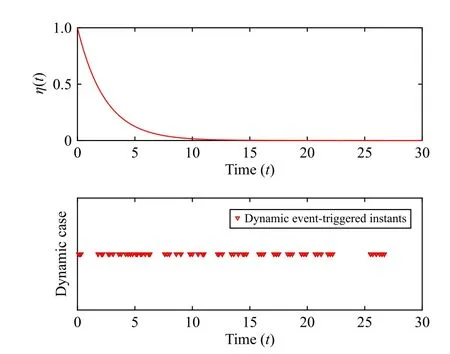
Fig.3.The trajectory of η(t) and event-triggered instants.

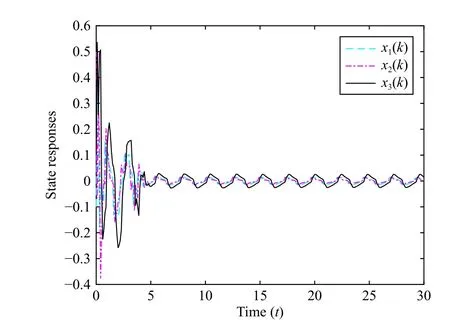
Fig.4.State trajectories of the closed-loop system under SETM.

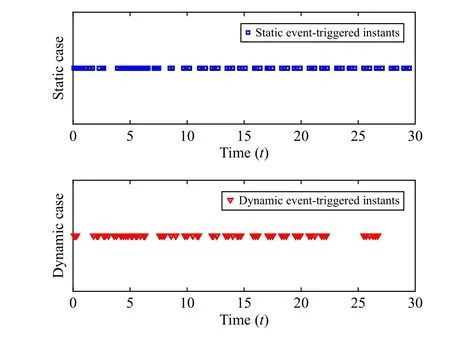
Fig.5.Event-triggered instants of DETM and SETM.

V.CONCLUSIONS

In this paper, the ISS and iISS analysis problems have been investigated for a class of networked systems subject to random impulses.The DETM has been adopted to relieve communication cost and improve communication resource utilization.By resorting to the sampling mechanism, the effects of impulses on the event-triggered scheme can be overcome.Then, with the help of stochastic analysis, a series of sufficient conditions have been derived to ensure the corresponding ISS and iISS performance.Subsequently, the explicit expression of desired controller gain has been also received by resorting to the solutions of linear matrix inequalities.Finally,the feasibility and validity of the proposed control approach have been verified by a simulation example.One of the future research topics is to extend our results to distributed impulsive systems under event-triggered-based sliding mode control schemes [42]–[45].