Coupled Dynamics and Integrated Control for Position and Attitude Motions of Spacecraft: A Survey

Feng Zhang and Guangren Duan,,

Abstract—Inspired by the integrated guidance and control design for endo-atmospheric aircraft, the integrated position and attitude control of spacecraft has attracted increasing attention and gradually induced a wide variety of study results in last over two decades, fully incorporating control requirements and actuator characteristics of space missions.This paper presents a novel and comprehensive survey to the coupled position and attitude motions of spacecraft from the perspective of dynamics and control.To this end, a systematic analysis is firstly conducted in details to show the position and attitude mutual couplings of spacecraft.Particularly, in terms of the time discrepancy between spacecraft position and attitude motions, space missions can be categorized into two types: space proximity operation and space orbital maneuver.Based on this classification, the studies on the coupled dynamic modeling and the integrated control design for position and attitude motions of spacecraft are sequentially summarized and analyzed.On the one hand, various coupled position and dynamic formulations of spacecraft based on various mathematical tools are reviewed and compared from five aspects,including mission applicability, modeling simplicity, physical clearance, information matching and expansibility.On the other hand, the development of the integrated position and attitude control of spacecraft is analyzed for two space missions, and especially, five distinctive development trends are captured for space operation missions.Finally, insightful prospects on future development of the integrated position and attitude control technology of spacecraft are proposed, pointing out current primary technical issues and possible feasible solutions.Index Terms— Coupled position and attitude dynamic modeling,integrated position and attitude control, position and attitude coupling analysis, spacecraft, space missions.

I.INTRODUCTION

SPACECRAFT, often represents self-contained, self-propelled and boosted vehicles flying in space, differently from aircraft designed to sustain itself in atmosphere above Earth’s surface [1].Generally, it contains upper stages of launch vehicles, orbital transfer vehicles or stages, spaceships,satellites and probes.

Spacecraft position and attitude represent the translational and rotational motions of a spacecraft, respectively, both of which play vital roles in various space missions.There exist complex mutual couplings between the position and attitude motions of a controlled spacecraft, which will be explained in details later.

According to the timescale difference between the position and attitude motions of spacecraft, space missions can be categorized into two types: space proximity operation (SPO) missions and space orbital maneuver (SOM) missions.

1) SPO missions mainly include rendezvous and docking(RV&D), spacecraft formation flying (SFF), on-orbit service,on-orbit observation, asteroid missions (hovering and flying around) and space debris de-tumbling and active removal.They focus on the relative position and attitude motions between a controlled spacecraft and a (virtual) target, holding the following features:

i) The position motion possesses a similar timescale as the attitude motion of spacecraft.

ii) Both the position and attitude motions of spacecraft have to satisfy specific requirements or constraints.

2) SOM missions mainly include orbit injection, orbital transfer, space rendezvous, interplanetary transfer injection,and planetary soft-landing.They focus on the inertial position and attitude motions of a spacecraft, holding the following features:

i) The timescale of position motion performs apparently different from that of the attitude motion of spacecraft.

ii) Mission mainly requires the spacecraft position to achieve an anticipated value and satisfy given constraints,while the spacecraft attitude should be controlled ensuring an appropriate thrust vector for the required position control.

Accurate position and attitude control is the key to the aforementioned space missions.In early space missions,spacecraft position and attitude motions are often separately controlled by neglecting their mutual couplings, as depicted in Fig.1, to reduce design complexity and improve mission applicability.The obtained control scheme should be iteratively modified based on spacecraft 6 degree-of-freedom(DOF) numerical simulations to fit control aims.With the emerging of various demands of access to space, space missions become more diverse and complicated.Considering that a space mission often comprises multiple flight stages,although the traditional separated position and attitude control philosophy could be still effective for a spacecraft flying in coast phases or the phases with low-performance control requirements, yet it might be gradually hard to provide satisfactory control accuracy and performance facing stringent requirements of some specified stages.The stages include,namely, the final approaching stage of RV&D and formation flying missions, the synchronized operation stage of on-orbit service mission, the hovering & flying around stages of asteroid mission, the de-tumbling & capture stage of active debris removal mission, the final flight stage of orbit injection and transfer, space rendezvous, interplanetary transfer injection and planetary soft landing missions.Besides the mission requirements, the mentioned iterative design mode only provides poor system design efficiency.

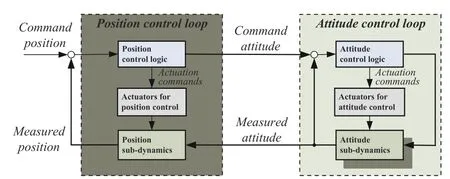
Fig.1.The sketch of the separated position and attitude control philosophy.

By virtue of this, arising from the integrated guidance and control (IGC) design philosophy for endo-atmospheric aircrafts, the integrated position and attitude control (IPAC) for spacecraft is then proposed in view of space mission features and the comprehensive recognition of spacecraft position and attitude mutual couplings.From the viewpoints of control design, as shown in Fig.2, the IPAC method takes spacecraft position and attitude motions as a whole and thus inherently ensures a good control accuracy, satisfactory performance,and high design efficiency, whereas in turns makes the controlled plant become a highly-dimensional, deeply coupled,even under-actuated nonlinear system, thereby bringing many challenges to the coupled dynamic modeling and integrated control design.

Fig.2.The sketch of the IPAC philosophy.

Research on the coupled position and attitude dynamics(CPAD) modeling and IPAC design for spacecraft started from 1990s and, after an initial feasibility study stage, has been gradually fruitful and distinctive, especially with the development of control theory and increasing recognitions on spacecraft dynamics.Until Jan.2022, about 222 related publications are found in Web of Science database and top-level conferences on aerospace or control.Some newly online-published literatures which are not yet included in the Web of Science database are also reviewed here.These publications are cumulated in Fig.3, where the black part represents the works on SPO missions while the red part denotes the works on SOM missions.The figure apparently shows that the numbers of publications on the CPAD modeling or the IPAC design for spacecraft are almost increasing year by year, especially after 2015.

In the light of this background, the present paper systematically reviews the state-of-the-art studies on the CPAD modeling and the IPAC design for spacecraft in terms of the above classified space missions.Firstly, the position and attitude mutual couplings for spacecraft are analyzed by fully incorporating adopted actuators, control requirements of missions,system uncertainties, and environmental effects.A technical summary and comparison is conducted for the CPAD modeling of spacecraft from the perspectives of mission applicability, modeling simplicity, physical clearance, information matching and expansibility.After that, the studies on the IPAC for spacecraft are summarized and reviewed for SPO and SOM missions, respectively.Finally, several insightful prospects are given for the future development of the IPAC technology, and several technical issues and possible solutions are proposed as well.

The main contributions of the present survey concentrate on the four parts as follows.

1) The position and attitude mutual couplings of spacecraft are analyzed in a systematic and logical way.Besides the traditional impacts from inherent dynamics and environmental disturbances, the influences of task-driven control commands and corresponding actuator schemes, involving selection, layout, and misalignment, are taken into account in details.Especially, the features of various actuator schemes are discussed for SPO and SOM missions to show the challenges for the IPAC design, respectively.

2) All the current modeling methods to formulate the CPAD of spacecraft are summarized and technically compared to show the suitable application scenarios of each method.In particular, based on a classical type of CPAD model, the proposed classification of space missions following the timescale difference in spacecraft position and attitude motions are mathematically and rigorously verified via normalization technique and singularly perturbed system theory.

3) The current studies on the IPAC technology for spacecraft are summarized and analyzed within the two proposed classification frameworks of space missions.Especially, five distinctive development directions are developed for SPO missions, while the technical bottleneck challenges are pointed out for the IPAC design of SOM missions.

Fig.3.The statistics of the studies on CPAD modeling and IPAC design of spacecraft.

4) Feasible technical solutions are twofold proposed to deal with the identified issues of the IPAC technology, highlighting its future development.The modeling aspect is considered to primarily focus on the mathematical modeling tools, actuators and non-rigid dynamics.On the other hand, from the viewpoint of control design, several promising methods are presented and discussed for SPO and SOM missions, respectively.

The framework of this survey is organized as shown in Fig.4.This section introduces the background and over statistical analysis of the review topic.In Section II, the position and attitude mutual couplings for spacecraft are recognized and analyzed to deduce four main coupling resources.Then, the current studies on the CPAD modeling for spacecraft are reviewed in Section III, where three main modeling methods are discussed and compared from five perspectives in details.Furthermore, the reviews on current various IPAC technologies of spacecraft are given in Section IV, where five development directions are summarized and analyzed in view of SPO missions.Based on the above reviews and analysis, Section V proposes future prospects of the IPAC technology from the modeling and control sides.Finally, Section VI draws the conclusion.

It is noteworthy that, although the IGC inspires the IPAC idea, yet there is a significant discrepancy between spacecraft and aircraft in flight environment, modeling architecture,dynamic features and control design philosophy.As a consequence, from the viewpoints of dynamics and control, the existing research achievements on the IGC design for endoatmospheric aircrafts are hard to be directly applied in CPAD modeling and IPAC design for spacecraft.Owing to this, the studies on the IGC for endo-atmospheric aircrafts will not be discussed herein.

II.POSITION AND ATTITUDE MUTUAL COUPLING ANALYSIS

Position and attitude mutual couplings bring many difficulties in dealing with the high-performance control problem of spacecraft conducting a given SPO or SOM mission.This section is firstly to identify these challenges from the perspectives of inherent dynamics, control input and uncertainties,since the three parts often constitute a control system.

1) From the viewpoints of dynamics, a complicated SPO or SOM mission often requires that the relative orientation of a spacecraft with respect to the mission target is determined not only by a pure rotation but also by an anticipated translation.In other words, the control commands from complex mission requirements lead to that the resulting coupled position and attitude dynamics formulation, describing the spacecraft motion relative to the mission target (or virtual target), often possesses to be highly dimensional and nonlinear.

2) From the control side, different selections and layouts of control actuator lead to various magnitude levels and directions of control inputs, including control force and torque vectors, thereby causing totally different position and attitude dynamic behaviors of spacecraft.

3) A large number of spacecraft uncertainties, such as environmental disturbances and modeling errors, often hold complex expressions involving both the position and attitude components, and thus would influence the control accuracy without a proper attenuation strategy.What is more, the reaction control based actuators are prone to generate additive couplings to affect control performance because the inevitable misalignment and control errors will induce additional disturbance torques.

The above recognition also clearly indicates that, for a controlled spacecraft conducting space missions, the position and attitude mutual couplings are mainly from four parts: control commands, control actuators, structure misalignment and control error, and environmental disturbances, which are then analyzed in details as follows.

A. Control Commands

Fig.4.The framework of the present survey.

As mentioned above, complex space mission planning inevitably leads to a coupled command position and attitude motion trajectory.Specifically, SPO missions often require the relative motion of a controlled spacecraft with respect to a target to track a given command relative position trajectory,such as fly around [2]–[4], RV&D [5]–[11], SFF [12]–[15], or keep in a constant distance, such as hovering [16]–[19], onorbit observation [20]–[22], on-orbit service [23]–[25]; and meantime, some installed components like cameras, antennas and operating mechanisms need to point to the target [5], [9],[11], [21], [25]–[28].By virtue of these, the command position will certainly involve attitude information and in turns the command attitude should be also determined by relative positions.What is more, taking into account spacecraft shape and target feature points would lead to further position and attitude kinematic mutual couplings to a greater extent [29], [30].Besides, for SOM missions, a command position and velocity corresponds to a required thrust vector, thereby determining a command attitude due to the dependence of thrust vector on spacecraft attitude [31]–[35].Especially, for planetary softlanding missions, the thrust vector should be designed to ensure not only pinpoint landing with a proper touchdown velocity but also vertical landing attitude [36]–[39].

B. Control Actuators

Due to providing required forces and torques for anticipated position and attitude motions, control actuator is a vital part of spacecraft position/attitude control system, and its selection, configuration and misalignment certainly bring different types of the position and attitude mutual couplings for the classified two space missions as follows.

For SPO missions, due to small timescale difference in position and attitude motions of spacecraft, unified thruster configurations are often utilized to provide required forces and torques [11], [19], [25], [40]–[53], and have been verified in experiments [54]–[57].Fig.5 illustrates a typical unified thruster configuration scheme enabling the IPAC for spacecraft, comprising totally six thruster pairs {Li,Hi}(i=1,2,...,6)[44]–[46].The thruster-based control method has been also applied in practice, such as NASA’s Apollo lunar module[58], ESA’s ATV spacecraft [59], JAXA’s ETS-VII spacecraft [60] and Hayabusa probe [19], China’s Shenzhou spaceship [61].Moreover, to improve attitude control accuracy,combined configurations of thrusters and flywheels or control moment gyroscopes are utilized in SPO missions [21],[62]–[65].For both configuration schemes, the position and attitude mutual couplings from the configuration and layout of actuators lie in the control allocation matrices in theory, which can be found in [44]–[46] for examples.

Fig.5.A unified thruster configuration scheme.

For SOM missions, due to significant timescale difference in position and attitude motions of spacecraft, large-thrust liquid propulsion engines are often installed on spacecraft as main thrusters to provide enough force for orbit maneuver.However, in view of complex structure and enormous size,main thrusters are not flexible to be configured and thus often installed along the longitudinal axis of spacecraft, together with required servo-mechanisms to enable thrust vector control.This configuration method has also applied in many spacecraft, involving NASA’s Centaur upper stages [66], the Interim Cryogenic Propulsion Stage of SLS launch vehicle[67], ESA’s EPS upper stage of Ariane 5 launch vehicle [68],the second stage of JAXA’s H-IIA launch vehicle [68], and the second stage of China’s LM-5 launch vehicle [69].Fig.6 illustrates such an configuration example comprising two main thrusters with four servo-mechanisms for thrust vector control.Notice that, it is enough to equip with main thrusters providing only several tens of or hundreds of kilograms for some spacecraft in SOM missions, such as China’s Chang’e family probes [70], [71], Yuanzheng family upper stages [72],and some satellites [35].In these occasions, main thrusters are often fixed on spacecraft body and together with extra attitude control thrusters ensure the required thrust vector for orbit maneuver.Totally, the layout of main thrusters and the corresponding servo-mechanisms or attitude control thrusters leads to a nonlinear relationship between the orbit maneuver oriented thrust vector and the spacecraft attitude motion.Also this relationship results in an important position and attitude mutual coupling for SOM missions and makes the obtained system dynamics to be under-actuated, bringing challenges for the IPAC design.

Fig.6.An actuator configuration scheme enabling thrust vector control.

C. Structure Misalignment and Control Error

Structure misalignment and control error inevitably bring position and attitude mutual couplings to spacecraft motions.On the one hand, structure misalignment mainly comprises the bias of spacecraft mass center and the actuator misalignment.The former causes asymmetrically configured thrusters to generate additional disturbance torques.Particularly, for SOM missions, even a tiny bias would cause a large attitude disturbance with the effect of main thrusters and thus degrade attitude tracking performance [33].The latter results in structural uncertainties in the control allocation matrices, thereby leading to additional forces and torques [44]–[46], [48], [56],[73]–[76].On the other hand, the real output of control actuator deviated from its nominal value gives rise to control error in the form of addictive disturbance force and possible disturbance torque in case that the spacecraft mass center does not belong to the thrust line [33].

D. Environmental Disturbances

Spacecraft suffers from various environmental disturbances,which also cause position and attitude mutual couplings given their analytic expressions.Although the coupling influence caused by space environment is not as large as the ones shown in the above three subsections, yet they should be not neglected to pursue higher control performance.Specifically,there are mainly three environmental disturbances causing position and attitude mutual couplings as follows.

1)The Oblateness of Centered Celestial Body: The oblateness of centered celestial body, such as the Earth, moon and other planets or asteroids, will induce perturbation on spacecraft position and attitude motions.Especially for asteroid proximity missions, the disturbance forces and torques caused by the irregular mass distribution of an asteroid become considerable [18], [19], [77]–[80].

2)The Gravitational Effects: The gravitational effects are related to the mass property and inertial position of a spacecraft.The resulting gravity force and gravity gradient moment perform to be complex functions of spacecraft position and attitude motions [9], [81]–[85].

3)Atmospheric Effects: For spacecraft flying in low earth orbit, the atmospheric force and torques will take effects and induce position and attitude mutual coupling effects [86].

Besides these three effects, other environmental disturbances possess less impact and thus are not taken into account herein for common spacecraft.

Remark 1: The above analysis shows a clear difference between spacecraft and endo-atmospheric aircrafts.The latter regards the atmospheric effects as a main mutual coupling resource, while for spacecraft, the position and attitude mutual couplings are mainly from control demands and actuators rather than the environmental effects.What’s more, in case of free-flying, there is weak position and attitude mutual couplings for spacecraft.In particular, the position and attitude motions of a spacecraft can be completely decoupled in the absence of environmental effects.

Remark 2: It should be noted that, for some specified spacecraft, environmental effects can even be used to enable an IPAC adhering to passive control design philosophy.For examples, by making full use of the position and attitude mutual couplings resulting from solar pressures, solar power satellites [87]–[89] and solar sails [90]–[94] are proposed to enable fuel-free flying.Moreover, the flying of electrodynamic tethered spacecraft [95]–[97] and Lorentz spacecraft[98] are controlled via the position and attitude mutual couplings caused by the interactions of a conductive tether and the geomagnetic field.

III.COUPLED POSITION AND ATTITUDE DYNAMIC MODELING

Based on different mathematical modeling methods, the CPAD modeling of spacecraft can be mainly classified into three types: separated-integrated coupled dynamic modeling(SICDM), CPAD modeling based on dual quaternion, and CPAD modeling based on Lie group SE(3).As shown in Fig.7,all three methods account for 97% of the current studies on the CPAD modeling for spacecraft.After a brief introduction,this section is to conduct a comparison for three modeling methods from the perspectives of mission applicability, modeling simplicity, physical clearance, information matching and expansibility.

Fig.7.The statistics of the CPAD modeling methods for spacecraft.

A. Separated-Integrated Coupled Dynamic Modeling

The main principle of the SICDM method lies in two steps:for the first, the position and attitude sub-dynamics of a spacecraft are respectively modeled based on appropriate mathematical tools, and are then incorporated to formulate a coupled dynamics by fully considering the position and attitude mutual couplings for a given mission.In view of its better modeling flexibility, the SICDM method develops a large number of study results for both SPO and SOM missions,which are analyzed twofold herein.

1)SPO Missions: The SPO missions often need to formulate a relative dynamics for a spacecraft with respect to a (virtual) target given a specific task.A typical coupled relative dynamic model by the SICDM method is given as follows[99], [100]:

The formulation in (1) covers most of the coupled relative position and attitude dynamics for SPO missions, holding superiorities in mission applicability, physical clearance and expansibility.

i)Mission applicability

If the dynamic formulation focuses on the spacecraft motion with respect to an inertial frame or a target orbit, then the formulated model in the form of (1) can be applied to the SPO missions involving cooperative targets, as the successive control design needs the target motion information.Especially,with proper variable transformations, a well-known Euler-Lagrange form can be obtained from (1) for SFF and some RV&D missions.Furthermore, once the relative position and attitude motion of a controlled spacecraft with respect to a target is considered within the spacecraft body frame or the lineof-sight frame, the target information is no longer necessary and instead the required information for control design can be directly obtained by the sensors (like CCD camera) fixed on the spacecraft.In this sense, the resulting relative dynamic formulation can be further applied to the SPO missions involving non-cooperative targets, holding a similar form to(1) whereas with more complex expressions of Λ,C,Dandn.The above classification can be found in Table I.

ii)Physical clearance

The dynamic model in (1) shows a good physical clearance.Especially, for spacecraft attitude motions, the SICDM method permits appropriate mathematical tools such as direction cosine matrix, Euler angles, quaternion, modified Rodriguez parameters, and Euler parameters, as accumulated in Table II.By comparisons, quaternion and modified Rodriguez parameters hold a wider application due to their good balance between singularity avoidance and computational efficiency, particularly considering large attitude maneuver in some SPO missions; Direction cosine matrix and Euler angles help to show a more clear physical sense, while the Euler parameters enable to facilitate a better mathematical formulation for pointing.

iii)Expansibility

The SICDM method can explicitly and completely describe the relationships between control inputs and actuator outputs.To show this, given a spacecraft scheme, the control input vectoru∈R6in (1) can be determined by the actuator output vectorT∈Rnand the control allocation matrixG∈R6×n(n≥6), i.e.,

where the matrixGis determined by the actuator layout and types, such as unified thruster configuration [19], [41]–[43],[52], [54], [57], [181], or combined thrusters/flywheels/control moment gyroscopes configuration [21], [63], [65].Moreover, the control allocation matrixGshould satisfyrank(G)≥6, which also corresponds to full actuation (r ank(G)=6) and over actuation (r ank(G)>6).

In addition, within the SICDM framework, more complex dynamic behaviors from flexible vibration [53], [103],[115]–[117], [121], [122] or liquid sloshing can be further formulated, ensuring a good expansibility.

2)SOM Missions: The missions often focus on the inertial position and attitude motions of a single spacecraft.A typical CPAD formulation based on the SICDM method for such missions is given as follows:

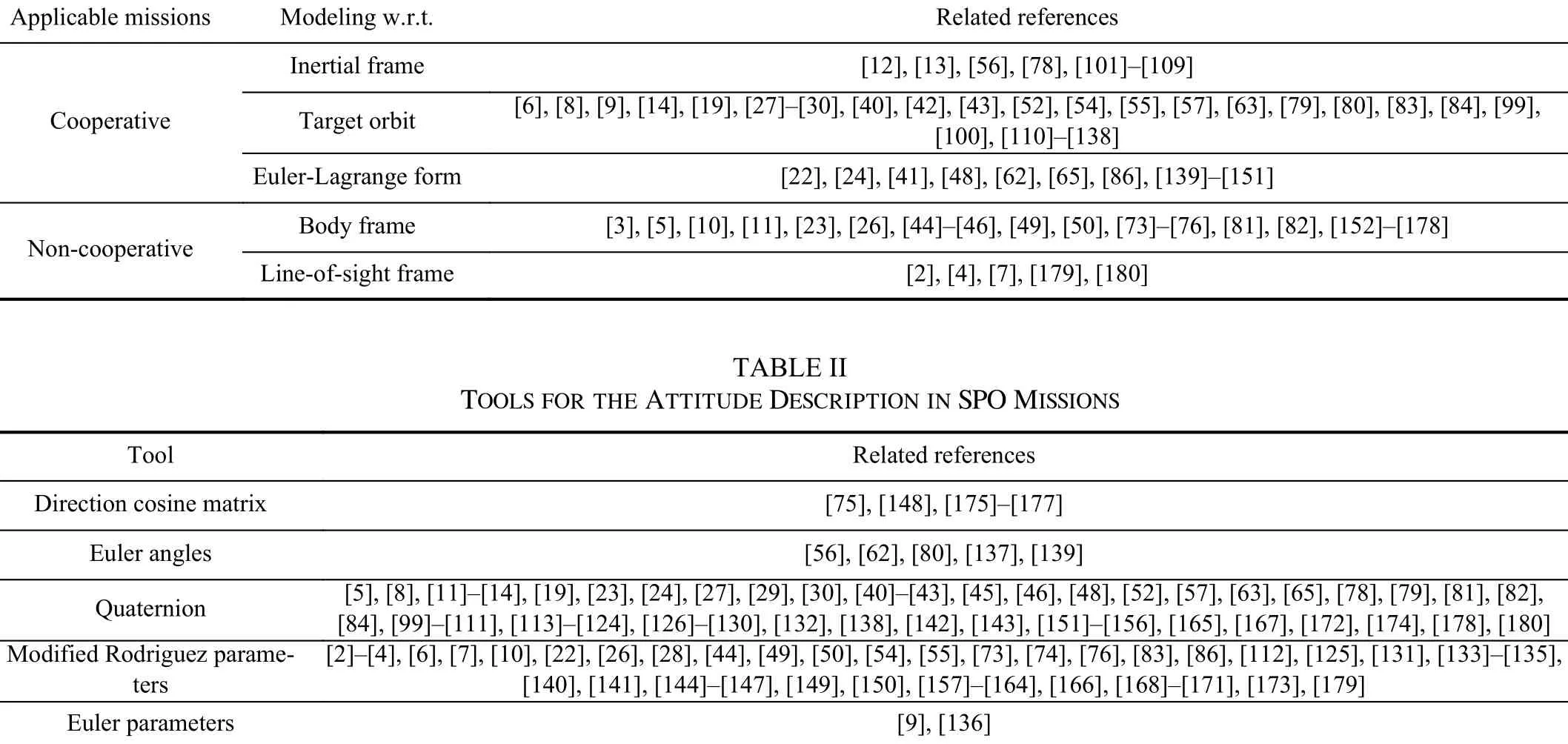
TABLE I MISSION APPLICABILITY OF THE SICDM METHOD FOR SPO MISSIONS

where the Euler angle vectorθdenotes the spacecraft attitude,fd,τdare the disturbance force and torque, respectively, andf(θ)represents the thrust vector depending on the spacecraft attitude, satisfying [33], [36]

in whichfdenotes the thrust magnitude andψ,ϕ are the yaw and pitch angles of the spacecraft, belonging to the vectorθ.

The formulation in (3) is capable of covering most of SOM missions, also holding superiorities in mission applicability,physical clearance and expansibility.

i)Mission applicability

The first two equations in (3) utilize Cartesian vectors to formulate the position dynamics of spacecraft in SOM missions, especially suitable for the short-duration SOM missions such as space rendezvous [31]–[35], [182], and planetary soft-landing [36], [38], [39], [183], [184].Meanwhile, for the long-duration SOM missions, especially the ones propelled by electric forces [185], [186], the classical orbital elements can be used to describe the position dynamics following the SICDM philosophy.

ii)Physical clearance

Similarly to SPO missions, the formulated dynamics in (3)following the SICDM philosophy also ensures a good physical clearance.Besides the position motion mentioned above,the spacecraft attitude can be also described by proper tools in terms of mission requirements, including Direction cosine matrix [34], [39], Euler angles [32], [33], [36], quaternion[31], [38], [182]–[185], modified Rodriguez parameters [186],and Euler parameters [35].It is noteworthy that the utilization of Euler angels or Euler parameters guarantees an appropriate expression of the thrust vector in SOM missions, which would greatly facilitate on-board computations and meanwhile reduce the computational burden of the successive IPAC design.

iii)Expansibility

The dynamics formulation in (3) completely and explicitly expresses the nonlinear relationship between thrust vector and spacecraft attitude, which also implies the under-actuated control feature of the CPAD of spacecraft in SOM missions.Additionally, within the modeling framework provided by (3),one can also further formulate more detailed dynamics according to specified SOM mission requirements and spacecraft features, such as the flexible vibration for solar power satellites [87]–[89], the coupled forces and torques resulting from solar pressure impacting on the large-area components of solar sails [90], [92]–[94], and the Lorentz effects coming from the interactions of electrodynamic tethers and the geomagnetic field for electrodynamic tethered spacecraft [95]–[97] and Lorentz spacecraft [98].

Remark 3: Based on the given two typical dynamics formulations in (1) and (3), we give a roughly theoretical explanation for the classification of space missions given in Section I.Without loss of generality, for a single spacecraft conducting SOM missions, consider the coupled dynamics formulation in(3) without external disturbances.Define the constants as follows:

whereHis the orbit height,REis the radius of the Earth, andμis the gravitational constant.Then the variable transformations

give a normalized form of (3) as

As a consequence, taking an SOM mission in low earth orbit as an example, the value of the time constantTcan be roughly computed as 0.001, which implies that the coupled dynamics in (7) can be deemed as a two-timescale singularly perturbed system [187], where the position and attitude motions of the spacecraft become slow- and fast-response subsystems, respectively.This in theory shows the significant timescale discrepancy between the position and attitude motions of spacecraft in SOM missions.By contrast, recalling (2) easily finds that the position motion possesses a similar timescale to the attitude motion of spacecraft in SPO missions, and thus the small timescale difference makes it hard to find an effective normalization as (7).

B. Coupled Dynamic Modeling Based on Dual Quaternion

According to Chasles theorem [188], one of the most fundamental results in spatial kinematics, the general displacement of a rigid body in space consists of a rotation about an axis(called the screw axis) and a translation parallel to that axis.Thus, the general displacement, also named as screw motion,including the position and attitude of the rigid body, can be represented via an appropriate compact mathematical tool,such as Lie algebra, dual quaternion and others.As an effective modeling tool, dual quaternion is developed from the conventional quaternion and holds a simpler form enabling to simultaneously represent the position and attitude motions of a rigid body.

In 1990s, Brenets, the chief designer of the control system of Russian Soyuz spaceship, firstly introduced dual quaternion into aerospace field and published the study on the strapdown inertial navigation system based on dual quaternion in[189].However, due to the language reason, in 2005, dual quaternion began to attract attention marked by [190].Although the reference mainly focuses on a new navigation algorithm by using dual quaternion, yet the formulated coupled position and attitude kinematics for rigid spacecraft,given as follows, indeed starts the studies on the CPAD modeling and IPAC design of rigid spacecraft based on dual quaternion

Based on the kinematics formulation in (8) and successive definitions of dual inertial operatorMˆ and dual forceFˆ, the CPAD of a single rigid spacecraft can be formulated in the form of twist as [21], [191]–[197]

where the dual forceFˆ=f+ετ totally represents the total force and torque acting on the spacecraft.

Furthermore, the coupled relative position and attitude kinematics and dynamics of a rigid spacecraft with respect to a target can be derived based on dual quaternion from (8) and (9)as

where the subscriptsfandlrepresent the spacecraft and the target, respectively.The formulation in (10) has been applied in SPO missions involving multiple spacecraft, such as SFF missions [15], [64], [193], [198]–[205], asteroid mission [18]and other SPO missions [20], [25], [53], [206]–[221].

The dual quaternion based dynamics composed of (8) and(9) has been also applied to some SOM missions like planetary soft-landing mission [37], [222]–[225], but it is noteworthy that various constraints, including thrust vector constraint,safe landing path constraint, angular rate constraint and lineof-sight constraint, have to be additionally described based on dual quaternion.

Compared with the SICDM method, the CPAD modeling based on dual quaternion ensures a simpler and more compact formulation, yet there remain some issues as follows.

1)Mission Applicability: Dual quaternion ensures a more effective description of the coupled position and attitude mutual couplings of spacecraft in kinematics.However, as for dynamics, as shown in (10), the complex control matrix and input function related to a specified actuator configuration can not be fully formulated and analytically expressed in the modeling framework.Especially, for some thrust vector control based SOM missions, it is difficult to effectively and explicitly formulate the nonlinear relationship between thrust vector and spacecraft attitude by dual quaternion.In this sense, dual quaternion would be more applicable for space missions with fully/over actuated spacecraft.

2)Physical Clearance: Necessary physical variables and functions in the form of dual quaternion, such as the mass property, force/torque, environmental disturbance, system uncertainty, should be redesigned to complete system modeling, analysis and control design.What’s more, as shown in (8)and (9), the values of the real and dual parts of a dual variable hardly provide direct physical meanings.Besides, to apply the well-known Lyapunov stability analysis theory, the Lyapunov-like function and equilibrium have to be redefined within the framework based on dual quaternion.These newly defined variables and functions perform a less clear physical sense compared with the SICDM method.Besides, the corresponding mathematical operation principles should be derived from classical Cartesian vector operations, which brings extra efforts and computational burdens.

3)Information Matching: In applications, the position and attitude information acquired by sensors involving inertial measurement unit and CCD camera are still three dimensional vectors in Euclidean space rather than dual quaternion.To match the required information format of the control design based on dual quaternion, a data transformation is indispensable for information matching.On the other hand,for a dual force, it is not feasible to directly apply its value to drive actuators as command inputs, unless there is a matching procedure to enable control allocation and command computation.

4)Expansibility: The CPAD modeling method based on dual quaternion mainly performs effective for rigid spacecraft,but hard to further cover non-rigid dynamic behaviors such as flexible vibration, liquid-sloshing and other dynamic motions for new conceptual spacecraft like solar sails or tethered spacecraft.Reference [216] tries to regard the flexible vibration as disturbance and introduces it into the model in (10),but does not additionally formulate the flexible dynamics based on dual quaternion.

C. Coupled Dynamic Modeling Based on Lie Group SE(3)

Inherited from quaternion, the potential unwinding phenomenon caused by dual quaternion may result in singularity during computations.To settle this issue, due to the singularity-free description for attitude motion, direction cosine matrix is utilized together with a position vector to construct a unified matrix belonging to a Lie group SE(3) in three-dimensional Euclidean space as follows to simultaneously describe the position and attitude motion of a spacecraft [226]–[228]

whereRis the direction cosine matrix representing the spacecraft attitude while the vectorrdenotes the spacecraft position.

By using the description based on Lie group SE(3), the coupled position and attitude kinematics of a single rigid spacecraft can be formulated as

based on which, with the definition of a total force vector and a mass property matrix as follows:

the coupled position and attitude dynamics of the single spacecraft can be formulated based on Lie group SE(3) as

Furthermore, based on (12) and (14), define the relative states between the spacecraft and a target in the form of Lie group SE(3) as

and introduce an exponential coordinate on SE(3), i.e.,, so the coupled relative position and attitude dynamics based on Lie group SE(3) can be formulated as [226]–[232]

The dynamics formulation given in (16) can cover most of SPO missions, including rendezvous and maneuver [226],[233], [234] and SFF [228], [230], [235]–[238].Moreover,more system uncertainties can be formulated into this modeling framework, such as gravity effects [47], [85], [226],[239]–[241] and the oblateness of Earth or asteroids [16],[17], [51], [85], [227], [229], [231], [232], [237], [240].

By comparisons, the modeling method based on Lie group SE(3) also ensures a simple form as the one based on dual quaternion, but effectively avoids the unwinding phenomenon.Moreover, the mathematical operations based on Lie group SE(3) naturally obey Euclidean principles since the Lie algebra of Lie group SE(3) is isomorphic to the vector space in six-dimensional Euclidean space.This facilitates the applications of conventional mature nonlinear design techniques in Euclidean space to avoid new definitions of variables and complex operation principles.However, the introduction of exponential coordinate brings a nonlinear relationship with respect to spacecraft position and attitude motions, which is hard to ensure a physical clearance.Moreover, the modeling method based on Lie group SE(3) has the similar drawbacks as the one based on dual quaternion, from the aspects of information matching and expansibility, which are no longer explained herein.

D. Discussions

Based on the aforementioned analysis, Table III gives a summary and comparison of the above three modeling methods.In addition, other mathematical tools are also tried to formulate the CPAD of spacecraft, namely, Cayley form [242],[243], twistor [244]–[247], and 2×2 unitary groups (DU(2))[248].The Cayley form results in a complicated dynamics formulation, thereby restricting its applications.The modelings based on twistor and DU(2) essentially are the same as the one based on dual quaternion, because twistor is indeed developed from dual quaternion and DU(2) is isomorphic to dual quaternion.

It should be noted that, as the formulated dynamics models are unrepresentative, either the CPAD modeling or the IPAC control design in the next section for spacecraft (like solar power satellites, solar sails, tethered spacecraft and Lorentz spacecraft) is not considered in the statistical analysis, though it can be conducted within the modeling framework in (3).

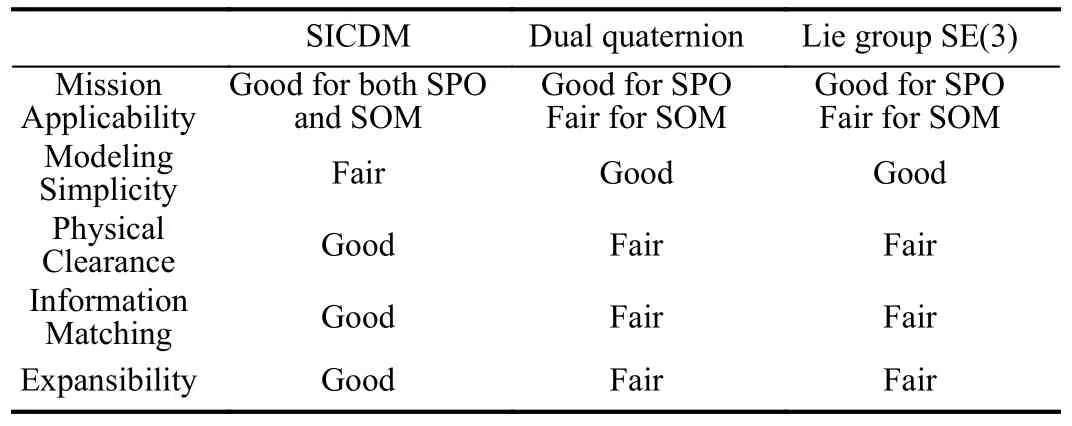
TABLE III THE COMPARISON OF THREE MODELING METHODS

Remark 4: In fact, the dual quaternion method originated from the framework of unit quaternion, which is isomorphic to a special unitary Lie group SU(2).Therefore, from the perspective of differential geometry, both the dual quaternion and SE(3) can be considered to belong to Lie group method and thus possess similar features as shown in Table III.Despite this, they are separately considered and analyzed herein because the resulting dynamics formulations greatly differ in analytically mathematical expressions and meantime the corresponding successive control designs hold different philosophies.

IV.INTEGRATED POSITION AND ATTITUDE CONTROL OF SPACECRAFT

The IPAC design of spacecraft is closely related to space mission requirements and control actuator configurations.Recalling Fig.3, it can be concluded from the statistics of the IPAC studies that 1) there is a large number of studies on SPO missions, accounting for a percentage of up to 91.8%, which is mainly due to the full/over actuation features; and 2) there is a few studies on SOM missions, only accounting for a percentage of 8.2%, because the under-actuation possessed by the formulated dynamics in SOM missions brings technical challenges in control designs.

A. SPO Missions

As mentioned in Section I, the actuator configuration for the spacecraft in SPO missions enables the position and attitude control system to be fully or over actuated.Notice that,although some references do not specify actuator configurations, yet the successive control design assumes that the control input satisfies rank(u)=6 enabling 6-DOF control, which is in fact equivalent to the full or over actuation.

This actuation feature ensures a wide variety of studies on the IPAC for spacecraft in SPO missions by using mature nonlinear control design techniques.Furthermore, in recent years,various platforms for ground tests have been developed to verify proposed IPAC algorithms, such as 6-DOF testbed [137],air-bearing 5-DOF test bed [56], [57], [249], and air-bearing 3-DOF test bed [250].These effectively improve the technology readiness level of the IPAC technology for SPO missions.

In view of the technical development, early studies on the IPAC for SPO missions mainly focus on its feasibility, and gradually, the changing mission features and various requirements lead the successive IPAC studies to show multiple features in five directions, including motion maneuverability,mission complexity, flight robustness, fuel cost and spacecraft control actuation, as shown in Fig.8.

Fig.8.Five development trends of the IPAC technology for SPO missions.

1)Motion Maneuverability: The control design in early stage of feasibility studies is mainly to make the position and attitude of a spacecraft asymptotically converge to command values.To this end, conventional nonlinear control techniques,including sliding mode control [41], [100], [152], [154], PD plus control [13], [54], [100], backstepping control [100],[123], and adaptive control [139], are utilized to deal with space debris removal, SFF, and asteroid hovering missions.The proposed IPAC schemes in these literatures ensure an asymptotic closed-loop stability within the well-known Lyapunov design framework, which is also applied to handle with the IPAC problems formulated by other mathematical tools,involving dual quaternion [192], [194], [195], [200], [210],Lie group SE(3) [226], [229], [230], [236], [239], and twistor[244], [245].Differently from the Lyapunov design framework, the asymptotic closed-loop stability is also proved based on Matrosov’s Theorem [62], [83].Moreover, a further closed-loop exponential stability is ensured by Contraction theory [140], improving the convergence of spacecraft position and attitude errors.

With the increasing requirements for the maneuverability of SPO missions, such as fast RV&D, fast formation re-construction and fast position and attitude stabilization of an assembly,the aim of the IPAC design gradually shifts from the asymptotic or exponential convergence to finite-time convergence of spacecraft position and attitude errors.To do so, as shown in Table IV, various non-smooth terms are effectively utilized to enable finite-time control:

i) On the one hand, non-smooth functions such as fractional or piecewise functions are introduced in conventional backstepping design procedures to ensure the finite-time closedloop stability [4], [49], [118], [168], [191].

ii) On the other hand, the terminal sliding mode control methods are proposed to incorporate various fractional func-tions of spacecraft position and attitude errors into the conventional sliding mode design enabling feasible finite-time control.The terminal sliding mode design is the key technique for this method and mainly consists of four types: two-term typeSII[3], [9], [16], [22], [48], [128], [151], [166], [198], [199],[201], [203], [241], three-term typeSIII[2], [7], [23], [47],[127], [170], [204], [233], [234], [237], [238], multiple-term type [148], and integral type [149], [173].The first two types of terminal sliding modes account for a large portion with the basic forms as follows, respectively:

TABLE IV THE STATISTICS OF THE IPAC STUDIES AIMING AT MANEUVERABILITY

TABLE V THE STATISTICS OF THE IPAC STUDIES AIMING AT CONSTRAINT INCLUSIVE CONTROL DESIGN

whereedenotes the spacecraft position and attitude error vector,r∈(1,2) is a prescribed fractional number,sigr(e)=[|e1|rsign(e1) ··· |en|rsign(en)].The finite-time control design st based on terminal sliding modes in (17) has been extended to tackle with the IPAC problems based on other mathematical tools, including dual quaternion [198], [199], [201], [203],[204], [215] and Lie group SE(3) [16], [17], [47], [85], [170],[233], [235], [237], [238], [240].By contrast, the complicated forms of the multiple-term and integral terminal sliding modes restrict their applications.

Another finite-time control design method follows the reference trajectory tracking philosophy.Specifically, a prescribed finite-time convergence trajectory of spacecraft position and attitude error is firstly designed based on initial system values,and then appropriate control techniques are utilized to construct a nonlinear tracking control law.Thus if the actual position and attitude of spacecraft can track the prescribed trajectory in finite time or all the time, then the finite-time convergence of the position and attitude errors can be obtained.A proper prescribed trajectory is the key of this method and is mainly designed by using polynomials [44], [46], [144], timevarying sliding manifold [64], [65] and Tanh function based time-varying manifold [178].

2)Mission Complexity: The IPAC of spacecraft for early stages is mainly to reach the position and attitude commands given by various requirements of SPO mission, including operations for international space station [40], RV&D [182],space debris removal [152], [153] and SFF [12], [62], [100],[139], [154].But for this stage, there is not much targeted design to deal with possible mission constraints like control limit, though it has been recognized during the mission analysis [12], [182].

As the increasing complexity of SPO missions, various constraints have begun to be recognized and handled, as shown in Table V.Current recognized constraints mainly consist of control constraint, motion constraint and measurement conraint.

As a common constraint, control constraint often refers to the limited magnitude of control actuator outputs.There are mainly two ways to deal with this constraint:

i) Construct a filter to introduce the control error caused by saturation in the control-loop to compensate the saturation impact.Most of such filters are developed from the antiwindup technique for linear saturated control systems [4],[45], [53], [120], [147], [156], [161], [162]–[164], [169],[171], [178], [179], while the filter can be also designed by using the RBF neural networks [79], Nussbaum function[175], [177] and disturbance observers [131], [162], [164],[174]

ii) Another method lies in the elegant design of the IPAC law to ensure the resulting control input is less than its limit[8], [138], [207].

Besides the magnitude limit, actuator dynamics is also taken into account in the IPAC design of a RV&D mission [133],while the time-delay of control input for an SFF mission is settled in [204].

TABLE VI THE STATISTICS OF THE IPAC STUDIES AIMING AT ROBUSTNESS

Motion constraint in SPO missions often contains collision avoidance, pose constraint and line-of-sight field constraint.For the collision avoidance, various artificial potential field functions are constructed [8], [10], [11], [15], [114], [148],[165], [170], [180], [205], [213], [221], [227], [235], [246]–[248] and applied in the IPAC design to ensure collision-free motions of multiple spacecraft in SPO missions such as RV&D and SFF.To cope with pose constraints for flight safety of spacecraft, like the approach corridor during RV&D,the barrier Lyapunov function is introduced in the IPAC design to ensure an admissible position and attitude motion range of spacecraft [4], [147], [163], [179].Moreover, to simultaneously deal with multiple constraints involving lineof-sight field, collision avoidance and thrust limit, trajectory planning [6], [9], [132] and model predictive control (MPC)[102], [134] are two effective methods to give feasible solutions.In addition, as the emerging of artificial intelligence technology, the reinforcement learning technique is used to solve the same problem and meanwhile ensures an online approximation of optimal control solution [217].

3)Flight Robustness: Early studies do not consider the impact from various system uncertainties on control accuracy and performance.However, to meet more stringent control requirements of SPO missions, it is necessary to analyze and deal with the system uncertainties resulting from environmental disturbances, unknown mass properties, unmodeled dynamics, actuator misalignment and control faults, as shown in Table VI.

Generally speaking, the conventional nonlinear control law based on PD plus feedward compensation possesses a certain stability margin, capable of providing satisfactory control performance facing simple-form environmental disturbances without any additional targeted design [62], [83], [100], [114],[126], [210].In terms of norm bounded time-varying environmental disturbances, with proper linearization,H∞control technique is then introduced to enable disturbance attenuation for the linearized attitude and position subsystems in [40] and[110], respectively.Meanwhile, L2-gain is introduced to evaluate the disturbance attenuation level for the nonlinear-form coupled position and attitude control systems [159], [160].Moreover, the MPC philosophy is also used to provide an iterative control process reducing the disturbance impact and improve system robustness to some extent [42], [84].

For the SPO missions with unknown mass properties, adaptive control technique would be a good solution.The conventional adaptive strategy is based on the certainty-equivalence principle to possess simple and easy design [28], [56], [112],[139], [140], [144], [154], [196], [209], but it is hard to reach the control performance provided by the corresponding nominal control system.This is mainly due to that the estimates of mass properties are hard to converge to their true values since the persistence excitation is not satisfied [251].To deal with this issue, the conventional adaptive control procedure is modified [49] or combined with the concurrent learning technique[169], [171], [180], [211] for the accurate estimation of mass property parameters, thereby improving control performance.Moreover, to further get rid of the persistence excitation constraint, non-certainty-equivalence adaptive control techniques,represented by the immersion and invariance design, are gradually applied in the IPAC design framework of spacecraft[11], [145], [180], [208], [213].Compared to the certaintyequivalence adaptive strategy, the non-certainty-equivalence adaptive control scheme not only ensures the convergence of mass property estimation errors, but also renders the system states to converge to a stable differential manifold ensuring asymptotic closed-loop stability.

For SFF and asteroid missions, the effects resulting from the oblateness and gravity of centered celestial bodies are mathematically formulated in analytic manners, which can be further compensated by adding a feedforward term within an IPAC scheme to improve the disturbance attenuation performance [18], [154], [196], [209], [219], [246], [247].

For SFF, on-orbit service and RV&D missions, the visual sensors like CCD cameras are hard to provide high-quality velocity information, which necessitates the velocity-free IPAC design of spacecraft.To compensate the performance loss caused by velocity-free feedback control, various filters are constructed to estimate velocity information, such as nonlinear first-order filters [81], [82], [112], [131], [197], simple linear first-order filters [20], [206], and second-order nonlinear filters [24].The estimation performance of velocity is further improved to be asymptotic or even exponential by modifying filter structures [25], [214].Based on the active disturbance rejection control design framework, the extended state observer is also used to estimate spacecraft velocity information [241] and has been verified the effectiveness via ground test [137].

Especially, for the SFF missions involving multiple spacecraft, the IPAC design has to face the constraints related to communications, such as switching topology, time-delay, and bandwidth constraint.To deal with the first two constraints,the adaption laws have been proposed within integrated control design [86], [125], [238], while for the communication bandwidth constraint, event-triggered mechanism [193],[220], [228] and hysteresis logarithmic quantizer [232] are respectively introduced to alleviate the communication burden.

Besides the above specified uncertainties that can be effectively handled by targeted methods, there are most of other system uncertainties hard to possess analytic forms, including complicated environment perturbations, unmodeled dynamics and the disturbances caused by actuator misalignment and control errors.These system uncertainties are often summarized into a lumped disturbance, which is further handled mainly in two ways:

i) Various forms of observers are designed to give an effective estimation of the lumped disturbance, and the estimate can be then compensated within the IPAC design procedure to reduce the disturbance impact on the control performance [3],[4], [10], [22], [23], [41], [47], [103], [118], [128], [136],[138], [139], [141], [162], [164], [166], [215], [216], [219],[220], [228], [237]; meanwhile, fuzzy system [26], [234],[238] and neural network techniques [43], [161], , [172], [177]are also utilized to estimate the lumped disturbance.

ii) Bring a robust term into the IPAC scheme based on conventional control techniques to effectively attenuate the impact of the lumped disturbance.The robust term is often designed via an elegant combination of spacecraft position and attitude errors and sign functions to provide a domination effect compared with the lumped disturbance within the Lyapunov design framework [5], [8], [45], [63], [86], [120],[127], [144], [156], [165], [168], [170], [199], [201], [202],[212], [245].What is more, to relax the control requirements,diverse adaptive strategies are introduced to estimate the upper bound of the lumped disturbance during the construction of a robust term [17], [21], [48], [57], [64], [65],[73]–[76], [79], [85], [146], [149], [150], [157], [158], [163],[167], [168], [173], [175], [179], [203], [204], [207], [231],[240], [246].

At last, it should be noted that, as the concentration on the mission safety and reliability increases, the IPAC studies involving control faults have raised in recent years, but currently only focusing on the fault-tolerant control design [21],[64], [65], [162], [167], [168], [172], [175], [203] and fault estimation [53] rather than reconstruction strategies.

4)Fuel Cost: Fuel optimal control is also a study focus for the IPAC design of SPO missions.In fact, compared with the only focus on guidance fuel cost or attitude control cost, it makes a better sense in practice to take into account both costs within the IPAC design framework.Besides, the fuel optimal control design has to fully take into account the current level of the on-board computers due to their limited computational ability.

Since the CPAD of spacecraft in SPO missions is highly nonlinear, the performance index for the optimal control problem formulation is given as a quadratic function yielding

The solution of this infinite-horizon nonlinear control problem can be obtained by solving the well-known Hamilton-Jacobi-Bellman partial differential equation.To do so, based on a direct parametrization, the state dependent Riccati equation method is often utilized to obtain suboptimal control solution [27], [55], [124], [153], but this requires to solve the Riccati equation repetitively at every integration step.This problem has been overcome by theθ-Dmethod via the introduction of two groups of parameters θi,Di, thereby reducing computational burden.Theθ-Dmethod has been applied to provide fuel suboptimal solutions to the IPAC problem in space debris [116], [117], [155], tumbling target approaching [115],[121], [122], and SFF [14], [111], [113].Moreover, the parameterizations in theθ-Dmethod are also used to solve the Hamilton-Jacobi-Isaacs inequality and develop a robust optimal control in the presence of external disturbances [129],[130]

It is remarkable that, every control Lyapunov function solves the Hamilton-Jacobi-Bellman equation associated with a meaningful cost [252].In other words, if a Lyapunov function is obtained for a nonlinear system, the resulting optimal control law can be computed without solving the Hamilton-Jacobi-Bellman equation.This corollary inspires the utilization of the inverse optimal control method to obtain a feasible Lyapunov function and offer a globally asymptotic integrated position and attitude error stabilizing control law which is optimal with respect to the performance index (18) [142],[143].

The MPC method is another effective way to cope with the integrated position and attitude optimal control problem of SFF [42], [101], in-orbit assembly [218], and asteroid missions [52], [102], [214] in terms of the index (18), though the solution is hard to be globally optimal for the whole control process.For planetary soft-landing missions, the successive convex optimization technique is further introduced into the predictive control procedure to improve the solvability of the control solution in every step [102], [214].

Besides, the Gauss pseudo-spectral method has been also used in [119] to develop a fuel-optimal integrated position and attitude motion trajectory, but it is more suitable for reference trajectory design rather than on-line planning and control compared with the above methods.

5)Spacecraft Control Actuation: As mentioned previously,actuator is a key part for the IPAC of spacecraft, and both its static and dynamic characteristics determine the control design complexity and performance to a great extent.Due to the configuration flexibility and convenience for control design, current studies and applications often adopt unified thruster configurations [19], [25], [40]–[53], [56], [57], [249]or proper combinations of thrusters and flywheels [21],[63]–[65], [234] to provide necessary forces and torques enabling the IPAC of spacecraft in SPO missions.However,thruster-actuated control schemes have some problems [109]:i) large amount of fuel will be consumed and the life of spacecraft will be shortened; ii) owing to working in on-off mode,the hard nonlinearity of thruster will greatly affect the control accuracy; and iii) the plume effect caused by thrusters may have impact on spacecraft itself as well.As a consequence,novel actuation strategies should be developed to enable integrated control strategy for future SPO missions, especially ones requiring higher control accuracy and performance.

As a good alternative, momentum-exchange based actuator has become an area of intense research interest due to its excellent input/output linearity, better servo-control performance, and less or even no fuel consumption.Flywheels and control moment gyroscopes are two successful examples applying angular momentum exchange principle in accurate spacecraft attitude control.As for SPO missions, space manipulators comprising several links and joints are often mounted on spacecraft to complete various manipulation [253].The kinematic and dynamic coupling between motions of spacecraft and mounted manipulators has been recognized and further characterized.Based on this internal coupling effects,space manipulator is considered to stabilize spacecraft attitude during the operations of end-effector via reaction nullspace method, which has been tested in ETS-VII flight mission as well [254].Inspired by these works regarding spacecraft systems with manipulators, to make full use of the internal coupling motion, space manipulator has been gradually deemed as control actuator trying to conduct the IPAC of spacecraft, the feasibility and robustness of which have been initially verified [104]–[109], concluding that although the control capability of manipulator actuation is limited, the available satisfactory control performance provides a good solution to future SPO missions with higher control requirements.

B. SOM Missions

The statistical data given in Fig.3 shows that the IPAC studies for SOM missions start later than SPO missions almost 10 years and possess only a few results to date.This is mainly because the under-actuation feature of the CPAD of spacecraft in SOM missions restricts the applications of fruitful nonlinear control design techniques.

Moreover, by recalling the dynamics formulation in (3), it is hard to deal with the nonlinear relationshipf(θ) between thrust vector and spacecraft attitude within the conventional Lyapunov design framework.To tackle with this problem, a triangle function transformation [33], [36] and a matrix decomposition [32] are respectively proposed to enable the conventional backstepping procedures to successfully solve the IPAC problems of lunar soft-landing and space rendezvous missions.

Besides the backstepping technique, the MPC procedure provides two available solutions as well.On the one hand, a quasi-IPAC scheme is proposed by combining orbital propagation and attitude tracking into the predictive control procedures [31], [34], [35], [185], [186].For each control period, an attitude command for next period is computed from a required thrust vector enabling orbital control, and then the attitude tracking for the command is finished in next period.This scheme is easy to conduct in practice but does not essentially integrate the position and attitude control-loops of spacecraft.On the other hand, the successive convex optimization technique is introduced in the MPC procedures to solve the IPAC problem of planetary soft-landing missions, meanwhile ensuring multiple constraints, including safety constraints, angular velocity constraints, and thrust vector constraints [37]–[39],[183], [184], [222]–[225].

V.FUTURE PROSPECTS

Based on the above analysis and reviews, this section presents the existing issues in the current development of the IPAC technology and proposes potentially feasible solutions from the modeling and control design perspectives.

A. Modeling

1) In view of the comparisons shown in Fig.7, the SICDM method has a wide application, yet the modeling methods based on dual quaternion and Lie group SE(3) also have begun to attract increasing attention in recent years, capable of effectively promoting formulation compactness and mathematical efficiency.However, the related two modeling frameworks need to be further developed to cover more practical application scenarios, such as flexible vibration, liquid-sloshing and other non-rigid dynamic behaviors.Reference [216] is a good attempt, but more mathematical operations should be developed to complete the modeling framework architecture.

2) As a vital part, control actuator has also gained a rising attraction for the IPAC studies in recent decades.As mentioned in Sections II–IV, current studies mainly involve available configurations and attenuation strategies coping with misalignments, following which there are two aspects should be primarily considered in the future:

i) The selection and optimized layout of control actuators will be of great significance in applications, because it has to provide not only enough but also suitable control forces and torques, enabling a high-performance 6-DOF motion of spacecraft.However, only a few studies obtain some results with only thrusters, mainly involving minimum actuator number[255], allocation [256], controllability [257], optimal propellant mass consumption [258], and fault-tolerant configurations [259].These results indicate that even unified thruster actuation system design is a challenge to enable IPAC design,not to mention the spacecraft system including various types of actuators.Hence, in view of various existing actuators, the selection and allocation of combined actuators would be another future study point.Besides, taking into account the limited on-board computational ability, the studies on realtime algorithms to optimize the selection and allocation of actuators would be more applicable and appealing, especially in case that one or more actuators fail to work.

ii) The dynamics and various nonlinearities of control actuators should be another important topic besides the configuration, output error and misalignment issues.Comprehensive recognition and consideration of actuator dynamics during the control design would improve the applicability of the resulting IPAC schemes.Taking the servo-mechanism enabling thrust vector for SOM missions as an example, its dynamic and static performances directly affect the resulting IPAC capability in applications.Meanwhile, there are many types of nonlinearities during its working process, such as saturation,hysteresis, time-delay, and deadzone, which should be appropriately handled to achieve required control accuracy and performance.

3) Most of current studies focus on rigid spacecraft.However, from a practical viewpoint, spacecraft is often equipped with liquid-fuel tanks and flexible components and hence in fact not a complete rigid body.The resulting complex behaviors, such as vibration and liquid-sloshing, will bring additional position and attitude mutual couplings.Especially, the above problems become more apparent for space transportation stages like the Interim Cryogenic Propulsion Stage and the Centaur upper stage, because they usually hold a larger slenderness ratio than common satellites and are equipped with large-volume tanks.Although there are several practical measures in applications, yet it is of great challenge and significance to conduct the IPAC design considering the impact of complex dynamic behaviors caused by structural vibration and liquid-sloshing.

B. Control

1) For SPO missions, keeping an insight on the current various study results finds that the CPAD of spacecraft can be transformed into a second-order fully actuated control system via proper eliminations or order evaluation techniques.In fact,to deal with such a control system, the high-order fully actuated control system theory developed in recent years[260]–[272] would be a promising method.The IPAC control design based on the high-order fully actuated system theory together with parametrization can make full use of the system design freedom so as to satisfy multiple control objectives,thereby possessing potential superiority compared with current study results in view of future increasingly complex requirements of SPO missions.

2) For SOM missions, the current two methods mentioned in Section IV-B are effective but need to be further developed.

i) On the one hand, the cascaded feature held by the CPAD of spacecraft in SOM missions makes the backstepping philosophy as a natural and reasonable approach.However, with no doubt, the system high-dimension will result in a much complicated control form that is hard for applications.Meanwhile, the explosion of terms issue caused by the backstepping method will appear.Although it can be handled by the dynamic surface control and filtered backstepping techniques,yet the closed-loop stability in turns degrades to some extent,due to the introduction of a low-order filter to overcome the explosion of terms.To settle this issue, singular perturbation theory would be a potential solution.Based on the recognition of the timescale discrepancy for complex nonlinear systems, the IPAC design based on singular perturbation theory would promise a simpler and more effective control law with elegant selections of control parameters rather than the complicated and tedious control form based on conventional methods, which improves the availability and applicability of control design; what is more, it can ensure a rigorous closed-loop stability analysis, holding apparent advantages in theory and applications [187].Also, as mentioned in Remark 3, the obvious two timescales feature (maybe three or more timescales if a specified actuator dynamics is considered) held by the CPAD of spacecraft for SOM missions indicates that the singular perturbation theory may be a suitable approach.Besides the rigorous stability analysis, satisfactory transient performance should be further pursued for such complex underactuated nonlinear system.A novel model reference adaptive control scheme in [273] provides a feasible solution to deal with this issue, following the philosophy incorporating the robust adaptive strategy with prescribed performance control to ensure both the stability and good transient performance.

ii) On the other hand, from the viewpoints of applications,the optimization based predictive control method will be still an effective way.Especially, due to available optimized solution with a rapid computational convergence and the independence on initial value guess, the convex optimization would be the main technique and has been verified in soft-landing missions [38], [183], [184], [225], but the convex optimization problem formulation and the relaxation of complex constraints would be main technical challenges.

VI.CONCLUSIONS

The human demands on space are daily on the increase,leading that space mission performs various development trends, such as large scale, high reliability and complexity,possessing higher and more stringent requirements on the position and attitude control accuracy and performance of spacecraft.As a promising technology, the IPAC design has been gradually a focus in the aerospace field, and after over two decades, developed a variety of study results.The current IPAC studies fully incorporate the features of space missions and control actuators, though the original IPAC design philosophy comes from the IGC design for endo-atmospheric aircrafts.The present survey summarizes the current fruitful study results on the coupled dynamics modeling and integrated control for the position and attitude control motion of spacecraft, and proposes the future technical development trends, providing references for the future practical applications of the IPAC technology of spacecraft.