Distributed Adaptive Resource Allocation: An Uncertain Saddle-Point Dynamics Viewpoint

Dongdong Yue, Simone Baldi,,, Jinde Cao,,,Qi Li, and Bart De Schutter,,

Abstract—This paper addresses distributed adaptive optimal resource allocation problems over weight-balanced digraphs.By leveraging state-of-the-art adaptive coupling designs for multiagent systems, two adaptive algorithms are proposed, namely a directed-spanning-tree-based algorithm and a node-based algorithm.The benefits of these algorithms are that they require neither sufficiently small or unitary step sizes, nor global knowledge of Laplacian eigenvalues, which are widely required in the literature.It is shown that both algorithms belong to a class of uncertain saddle-point dynamics, which can be tackled by repeatedly adopting the Peter-Paul inequality in the framework of Lyapunov theory.Thanks to this new viewpoint, global asymptotic convergence of both algorithms can be proven in a unified way.The effectiveness of the proposed algorithms is validated through numerical simulations and case studies in IEEE 30-bus and 118-bus power systems.Index Terms—Adaptive systems, directed graphs, resource allocation, saddle-point dynamics.

I.INTRODUCTION

THE resource allocation problem, also known as the economic dispatch problem, has recently aroused multi-disciplinary interest.Applications of resource allocation include various engineering fields such as cloud computing, sensor networks, and power systems.While early works studied optimal resource allocation based on a central node collecting and processing all data from every node in the network [1], this architecture is not effective in large-scale networks.Therefore, distributed resource allocation algorithms are highly desirable, i.e., to solve an allocation problem by making each node collect and process the data from only a few neighboring nodes, according to the topology of the network.

Different assumptions can be made on the graph describing the large-scale network: acyclic (tree) graph [2], undirected connected graph [3]–[12], strongly connected weight-balanced digraph [13]–[18], or weight-unbalanced digraph[19]–[21].In most of these works, the algorithms used to solve the distributed resource allocation problem require unitary step sizes, or sufficiently small step sizes to implement local gradient descent, see e.g., [4]–[6], [17]–[20].Meanwhile,many algorithms rely on homogeneous and static coupling gains, selected based on the global knowledge of Laplacian eigenvalues, e.g., [7], [10], [14]–[17], [21].Such a strategy may lead to high-gain instability when the network is large and sparse (with a Laplacian eigenvalue being extremely close to the imaginary axis).Besides, for an effective distributed methodology, eliminating the global knowledge of the Laplacian matrix is crucial, which goes under the name of distributed adaptive implementation.

In fact, distributed adaptive algorithms incorporate adaptive(in place of static) coupling gains, which have the superiority of adapting to different network configurations.The reason is that these adaptive gains do not need to be selected based on global knowledge of Laplacian eigenvalues.Distributed adaptive designs with adaptive coupling gains are available in the literature for consensus or tracking [22]–[26], containment or formation [27]–[29], and optimization [30], [31].

Distributed resource allocation solutions with adaptive coupling gains, to our best knowledge, are not available in the literature, even for the simplest case of undirected graphs.The main reason for this gap lies in the following difficulty: In order to obtain an optimal resource allocation solution, the agents are supposed to seek a consensus over the Lagrangian multipliers based on a class of nested primal-dual dynamics[4].This strategy brings the challenge of individual seeking of optimal allocation decisions and consensus seeking of the Lagrangian multipliers at the same time, without any knowledge of Laplacian eigenvalues.A possible approach to address this challenge is to solve the consensus optimization problem for the Lagrangian multipliers via distributed adaptive optimization of [30], [31].Such an approach of focusing on the dual problem instead of the primal problem was indeed adopted in [11], [19], [20], but it may bring the so-called“two-time-scale” problem, as each agent needs to solve an auxiliary optimization problem at each time instant towards optimal resource allocation [4].The “two-time-scale” issue also exists in other approaches, see e.g., the alternating direction method of multiplies [32].

Motivated by the above discussions, this work studies distributed adaptive solutions to the resource allocation problem.We provide a novel perspective into this problem by showing that the optimal solution corresponds to the (generalized)equilibrium of a class of uncertain saddle-point dynamics.The basic idea to guarantee convergence to this equilibrium is to introduce heterogeneous adaptive coupling gains promoting consensus over the Lagrangian multipliers of optimal decisions, and to let the agents self-determine the coupling strengths between each other.To implement this idea, two distributed adaptive strategies are studied, i.e., directed-spanningtree-based (DST-based) and node-based: In the former, only the gains associated with edges along an DST are made adaptive; in the latter, the gains associated with all incoming edges for each node (so that all edges in the network) are made adaptive.The main contributions of this paper are as follows:

1) We propose a new point of view into the resource allocation problems, which is made possible by framing the problem via a novel class of uncertain saddle-point dynamics.We show that the optimal solution to the resource allocation problem corresponds to a generalized equilibrium point of the uncertain saddle-point dynamics, as discussed in Definition 1 and Lemma 6.

2) Inspired by the uncertain saddle-point dynamics viewpoint, we propose two novel distributed adaptive frameworks for solving optimal resource allocation over digraphs and prove their convergence in a unified way (Theorems 1 and 2).

3) Two novel classes of convexity conditions named spanning-tree-based strongly convexity and jointly strongly convexity are identified for the proposed algorithms, respectively.We also show a relatively standard class of local cost functions that automatically satisfies the proposed convexity conditions (Corollaries 1 and 2).

4) The proposed algorithms require neither sufficiently small or unitary step sizes, nor global knowledge of Laplacian eigenvalues, which are widely required in nonadaptive strategies proposed in the literature, see e.g., [4]–[7], [14]–[21].Besides, the proposed algorithms focus on the primal resource allocation problem directly: thus, the “two-timescale” issue in the duality-based literature [11], [19], [20] does not arise.

The rest of the paper is organized as follows.In Section II,we give the preliminaries and problem statement, and we introduce uncertain saddle-point dynamics for the problem.In Sections III and IV, two distributed adaptive resource allocation algorithms are established as DST-based and node-based,respectively.In Section V, simulations are performed to validate the theoretical results.Some discussions are presented in Section VI.Finally, Section VII concludes the paper and discusses some future topics.

II.PRELIMINARIES AND PROBLEM FORMULATION

A. Matrix Algebra

A series of technical lemmas useful for stability analysis is now introduced.The so-called Peter-Paul inequality will be frequently used throughout this paper to bound non-definite terms with positive definite expressions.

Proof: The lemma follows directly from the Young inequality with exponents 2 and a positive bias ϵ.■

The following lemma can be inferred from [22, Lemma 2.3], and will be used (cf.(39)) to analyze the node-based algorithm of Section IV.

Lemma 2: Suppose thatU∈RN×N.LetS∈Rn×nbe an orthogonal matrix andx=col(x1,...,xN) be an aggregated vector withxi∈Rn,i∈IN.Then,

whereyk=([S x1]k,[S x2]k,...,[S xN]k)T,k∈In.Here, [S xi]kis thek-th entry of the vectorS xi.

B. Algebraic Graph Theory

The graph theory notation allows us to introduce two lemmas useful for stability analysis.Lemma 3 will be used to analyze the DST-based algorithm of Section III.Lemma 4 will be used to analyze the node-based algorithm of Section IV.DS TG¯.Then,the following statementshold:

Lemma3([28],[34]):ConsideradigraphG that contains a

1) The Laplacian L has a simple zero eigenvalue corresponding to the right eigenvector 1N, and the other eigenvalues have positive real parts.

2) Define a matrixΞ ∈R(N-1)×Nas

Remark 1: The existence of the matrixQis guaranteed by Lemma 9 of [35], and the uniqueness ofQis guaranteed by the fact that Ξ has full row rank.

Lemma 4([25],[36]): Suppose G is strongly connected.Then, the following statements hold:

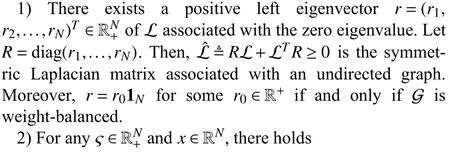
3)[Courant-Fischer] In thespecial casethatςis chosenas 1N,i.e.,theeigenvector of Lˆassociated withthe zero eigenvalue, then

C. Problem Statement

ConsiderNagents interacting over a digraph G.Each agent has an amount of local resourcesdi∈Rnand is associated to a local cost functionfi(·):Rn→R.In distributed resource allocation, the agents are cooperatively seeking a global allocation strategy with minimum cumulative costf(·):RNn→R(referred to as the global cost function), while meeting the sum of the total resources

The following assumption is standard in the distributed resource allocation literature, see e.g., [4], [6], [11], [17].

Assumption 1: Each local cost functionfi(·) is continuously differentiable and strictly convex.(1) has a unique solutionx∗.Moreover, there exists a uniquey∗∈Rn, i.e., the Lagrangian multiplier, such that

Lemma 5(Solution of(1)): Under Assumption 1, problem

where ∇f(x)=col(∇f1(x1),...,∇fN(xN)) according to the definition off(·) andD=col(d1,...,dN).

Remark 2: Equation (2) is known in the literature as the Karush-Kuhn-Tucker (KKT) condition (see e.g., [37, Chap.5]).Specifically, given the Lagrangian function of problem(1), i.e.,L(x,y)=f(x)+yT(1TN⊗In)(x-D), the KKT condition (2) consists of ∇xL(x,y)=0 (tangency) and ∇yL(x,y)=0(feasibility).

In this paper, the following assumption is made regarding the communication graph.

Assumption 2: The communication digraph G is strongly connected and weight-balanced.

Remark 3: This assumption is standard in distributed resource allocation as well as distributed optimization problems [14]–[18], and is considerably more general than the assumption of G being undirected and connected [4]–[12].Note that there have been some results on weight-unbalanced digraphs [19]–[21], which require sufficiently small step sizes for gradient descent and can raise the “two-time-scale” issue[19], [20], or rely on constant coupling gain selected according to the Laplacian eigenvalues [21].These limitations are not desired for an effective distributed methodology.Note that, if G is weight-unbalanced, one can recover Assumption 2 by first performing a finite-time weight-balancing algorithm along a DST, cf.[31].

D. Primary Analysis

To solve problem (1), one can in principle use saddle-point dynamics, i.e., a gradient descent of the Lagrangian functionL(x,y) in the primal variablexand a gradient ascent in the dual variabley0∈Rn

However, one problem of (3) is that the update ofy0cannot be performed in a distributed way.To make the saddle-point algorithm (3) distributed, several algorithms have been proposed,suchas endowing eachagentacopyofthe dualvariable asyi∈Rn,i∈V,while incorporatinganintegralfeedback action ofyi, see [4], [17].

Therefore, let us consider the system resulting from incorporating a distributed integral feedback action of local dual variables on top of (3), as follows:

Remark 4: State-of-the-art distributed algorithms to solve problem (1) directly involve the Laplacian matrix L in place of Υ (see e.g., [4], [17]).However, a unitary step size of the gradient descent is required and, in the case of [17], the global knowledge of Laplacian eigenvalues is also required.

Let us define the generalized equilibrium points (GEP) of the uncertain system (4) as follows:

Definition 1(GEP): The tripleis called a generalized equilibrium point of (4), if for any, there holds O |(x˜,y˜,z˜)=0.

Lemma 6(GEPs of(4)): Under Assumptions 1 and 2, the uncertain system (4) has infinitely many GEPs.Moreover, if

Lemma 6 states that distributed optimal resource allocation can be realized by steering the uncertain saddle-point dynamics (4) to its GEPs.In the following two sections, we will propose two continuous realizations of Υ in (4b), that are DSTbased and node-based, respectively, and guarantee stable attractive behavior of the GEPs of (4).

III.DISTRIBUTED ADAPTIVE RESOURCE ALLOCATION:DST-BASED DESIGN

Recall that, with the strongly connected property, a DST can beidentifiedin a distributedfashion without any priorknowledge of theLaplacian matrix[38].Based on any DSTG¯ ofG,consider the distributed adaptive resource allocation (DARA)algorithm for agenti∈V,j≠i(k∈IN-1), as follows:

whereκ2∈R+and Lais the gain-dependent Laplacian matrix defined as follows:

The weightwijmultiplied by the gainaijdetermines the feedback gain of the relative error vector (yi-yj) for agentito updateyiandzi.Note that we did not defineaiiin (5) and (6)since there are no self-loops.According to (5d), the gainaijis updated only wheneji∈E¯.Such an update law is distributed,i.e., it depends on agenti, agentjand all the out-neighbors of agentiin the DST [24], [31].One can refer to Algorithm 1 for the implementation of (5).

Theorem 1: Under Assumptions 1 and 2, the adaptive algorithm (5) drives (x,y) to (x∗,1N⊗y∗) asymptotically for any initial condition (x(0),y(0),z(0)∈RNn×RNn×RNnand anyai j(0)∈R provided there exists a scalarm∈R+, such that the following condition (referred to as spanning-tree-basedmstrongly convexity) holds ∀x,y∈RNn:

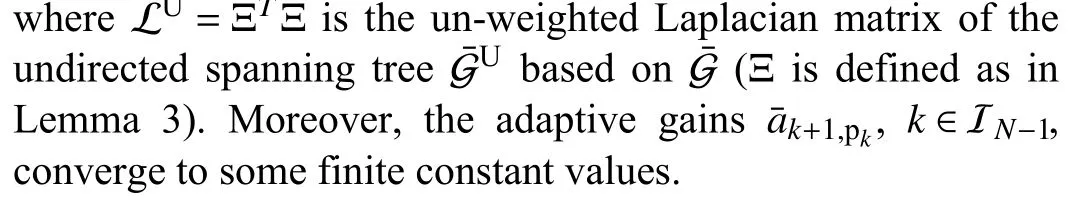
Algorithm 1 DARA: DST-Based Data: 1) Initialization: , , , ; 2) Parameters: , ;3) Structure: A DST xi →x∗Result: Optimal resource allocation solution s ←1 xi(0) yi(0) zi(0)aij(0) κ1κ2¯G(V, ¯E)1: ;2: while do /* h is the integration step and is the terminal time i ←1 s·h ≤Ttml Ttml 3: for to N do dxi ←-κ1(∇fi(xi)+yi)4: ;dyi ←xi-di- ∑Lai jyj- ∑5: ;dzi ←∑j∈V Lijzj j∈V 6: ;j ←1 j ≠i j∈V Lai jy j 7: for to N and do daij ←0 8: ;eji ∈¯E ∃k ∈IN-1 i=k+1 j=pk 9: if then /* such that and(yi-yc))T(yj-yi)10: ;daij ←κ2((y j-yi)- ∑c∈¯Nout(i)11: end aij ←aij+h×daij 12: ;13: end xi ←xi+h×dxi 14: ;yi ←xi+h×dyi 15: ;zi ←xi+h×dzi 16: ;17: end s ←s+1 18: ;19: end

Proof: We conduct the proof by showing that each trajectory of (5a)-(5c) converges to a GEP of (4).Let us define the error vectors between the trajectory of (5a)-(5c) and any GEP(x˜,y˜,z˜) of (4), following a change of coordinates:

Here, statement 2) of Lemma 3 and the properties of the Kronecker product have been used to get (9b) and (9c); and the fact that ( Ξ⊗In)y˜=0 has been used to get (9d).

Consider the following candidate Lyapunov function:

where

andQs>0 is guaranteed by 3) of Lemma 3, and ϵ1, ϕk+1,pk∈R+,k=1,...,N-1, will be determined later.

The time derivative ofVµ¯can be obtained as

By (8b) and (7), we have

Then,

whereϵ2∈R+is to be decided later, and Lemma 1 was used to get the second inequality.

The time derivative ofcan be obtained as

From (10), one has

Following the procedure in [24], [28] and [31], let us define Φ ∈R(N-1)×(N-1)as:

Then, it follows from (16)-(18) that:

Note that the time-varying matrixQ¯ahas been cancelled,and all the matrices left are constant.Based on Lemma 1, we have

where we have also used the property thatxT Ax≤λ¯(A)xT xfor a matrixA>0 and for allxto get the last inequality.

The time derivative ofVη¯can be obtained as

where we have repeatedly used Lemma 1 to get the inequality.

Based on (11), (15), (20), and (21) and with some manipulations, the time derivative ofV1along the trajectory of (9) is upper bounded by

whereγ ∈R+is given by

Substitute (5a) and (5b) evaluated at (xs,ys,zs) into the above, and note that Oa|(x˜,y˜,z˜)=0.Then, we obtain

Consider the special case of quadratic local costs

In this case, the spanning-tree-basedm-strongly convex condition (7) holds with anym≤λ(Θ) and for any DST.Immediately, we have the following corollary:

Corollary 1: Under Assumptions 1 and 2, the resource allocation problem (1) with local costs (28) can be solved with the adaptive algorithm (5) for any initial conditions (x(0),y(0),z(0)∈RNn×RNn×RNnand anyai j(0)∈R, i.e., (x,y)→(x∗,1N⊗y∗).Moreover, the adaptive gainsa¯k+1,pk,k∈IN-1, converge to some finite constant values.

Remark 5: The proposed adaptive resource allocation framework is essentially different from related literature [7],[10], [14]–[17], [21], which rely on the global knowledge of Laplacian eigenvalues to establish convergence results.The main idea behind the proof of Theorem 1 is to repeatedly use the Peter-Paul inequality (Lemma 1) so as to entrust stability to the adaptive coupling gainsa¯k+1,pk.Thus, global stability canbe derived byselecting sufficiently largeϕk+1,pkwith the helpof the Schurcomplement and mathematicalinduction, as shown in the proof.As a consequence, the knowledge of the global Laplacian eigenvalues is successfully removed at the design stage.Note that the exact values of the parameters ϕk+1,pk, ∀k∈IN-1, are not needed in the algorithm, they are only used for the purpose of stability analysis.

Remark 6: In addition to removing the knowledge of the global Laplacian eigenvalues as discussed above, it is worth noticing that the adaptive coupling gains (5d) overcome the need for unitary, or sufficiently small steps sizes to implement local gradient descent [4]–[6], [17]–[20].The convergence of the proposed algorithm (5) is guaranteed globally for any parameters κ1,κ2∈R+.These parameters can easily be tuned taking into account the fact that increasing κ1allows for larger step sizes towards decreasing the local costs (with constraint concerns), while increasing κ2enhances the import ance of communicating Lagrangian multipliers.Generally speaking, a larger κ1would require a smaller integration step for practical implementation (i.e., smallerhin Algorithm 1),and larger κ2would induce higher steady-state coupling gains(cf.our simulations in Section V).Note that the above discussions also apply to the node-based case in Section IV.

IV.DISTRIBUTED ADAPTIVE RESOURCE ALLOCATION:NODE-BASED DESIGN

The DST-based adaptive law (5d) in Section III relies on the structural information of a DST.Although a DST can be obtained in a distributed way [38], it is of interest to possibly remove this intermediate step: To this purpose, a node-based design is developed in this section.Consider the following distributed adaptive resource allocation (DARA) algorithm for agenti∈V:

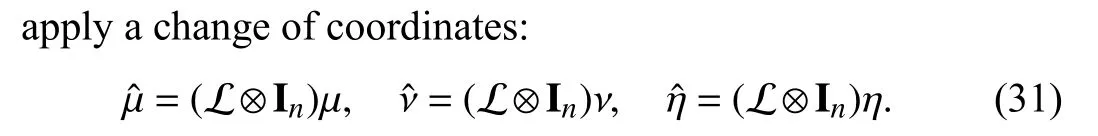
Algorithm 2 DARA: Node-Based Data: 1) Initialization: , , , ; 2) Parameters: ,xi →x∗Result: Optimal resource allocation solution xi(0) yi(0) zi(0) ai(0) κ1κ2 1: ;s ←1 2: while do /* h is the integration step and is the terminal time i ←1 s·h ≤Ttml Ttml 3: for to N do ξi ← ∑4: ;βi ←κ2ξTi ξi 5: ;dxi ←-κ1(∇fi(xi)+yi)j∈V Lijyj 6: ;dyi ←xi-di-(αi+βi) ∑Lijy j- ∑j∈V 7: ;dzi ←(αi+βi) ∑j∈V Lijzj 8: ;dαi ←βi j∈V Lijyj 9: ;xi ←xi+h×dxi 10: ;yi ←xi+h×dyi 11: ;zi ←xi+h×dzi 12: ;αi ←αi+h×dαi 13: ;14: end s ←s+1 15: ;16: end

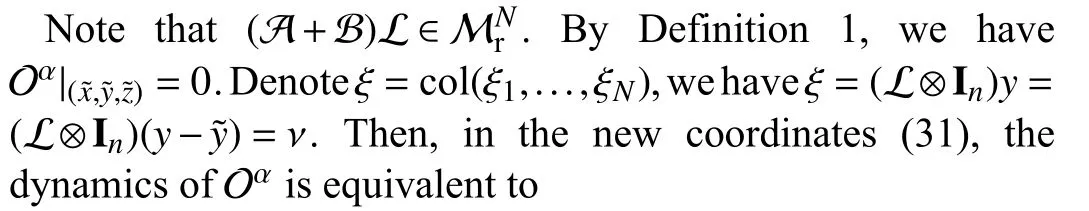
whereh=∇f(µ+x˜)-∇f(x˜) in (32a).

Consider the following candidate Lyapunov function:

where

whereα¯, ϵ1∈R+remains to be decided.

The time derivative ofVµ¯can be obtained as

By (31) and (30), we have

Similar to (15), we have

whereϵ2∈R+is to be decided later.

where we have repeatedly used Lemma 1 to get the second inequality.

Similar to (21), the time derivative ofVηˆcan be obtained as

Based on (33), (37), (41), and (42) and with some manipulations, the time derivative ofV2along the trajectory of (32) is upper bounded by

whereγ′∈R+is given by

implying thatV2has a finite limit and all the signals µˆ, νˆ , ηˆ,and αiare bounded.The rest of the proof follows similarly to that of Theorem 1.■

Note that for local costs (28), the jointlym-strongly convex condition (30) also holds with anym≤λ(Θ), resulting in the following corollary:

Corollary 2: Under Assumptions 1 and 2, the resource allocation problem (1) with quadratic local costs (28) can be solved with the adaptive algorithm (29) for any initial condition (x(0),y(0),z(0)∈RNn×RNn×RNnand any αi(0)∈R+, i.e.,(x,y)→(x∗,1N⊗y∗).Moreover, the adaptive gains αi,i∈IN,converge to some finite constant values.

Remark 7: Although both algorithms can be recast as uncertain saddle-point dynamics, the ideas behind the DST-based and node-based designs for promoting the consensus overyiare intrinsically different.In the DST-based case, the root of the DST plays the role of a leader; while in the node-based case, there is no leader and all the nodes play the same role.This shows the flexibility of the uncertain saddle-point dynamics viewpoint to accommodate for different design perspectives.

Remark 8: The proposed conditions, either the spanningtree-based or the jointly strongly convexity, are slightly more conservative as compared with classical strongly convexity.The reason is due to the induced Laplacian matrices.Nevertheless, Corollaries 1 and 2 have shown a relatively standard class of local cost functions that automatically satisfies the proposed strongly convexity conditions.

V.SIMULATIONS

In this section, we give two examples to show the effectiveness of the proposed methods.For each example, we consider two cases to model networks of different scales (cf.Fig.1).The first example considers cost functions with randomly generated coefficients, while the second example is inspired by the benchmark power networks IEEE 30-bus and IEEE 118-bus for which the systems diagrams and data sets are available online at [40] and [41], respectively.

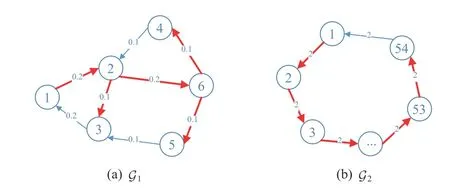
Fig.1.Two balanced digraphs.The selected DSTs for the DST-based protocol (5) are highlighted with thicker red lines.

In addition to validate the effectiveness of the proposed algorithms, some other goals of the experiments include: to support Remark 6 in that the convergence of the proposed algorithms is guaranteed globally for any parametersκ1,κ2∈R+; to highlight the necessity of introducing the adaptive coupling strategies; to give a comparison with the method proposed in [14].

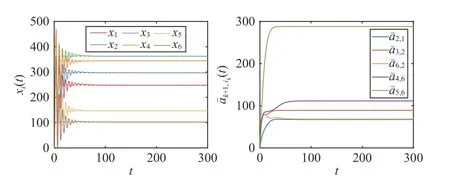
Fig.2.Case 1: States xi(t) of the agents and adaptive gains a¯k+1,pk(t) with DST-based protocol (5) and parameters κ1=κ2=1.The states xi(t) converge to the corresponding optimal allocation decisions, and the adaptive gains a¯k+1,pk(t)converge to finite constants.

Fig.3.Case 1: States xi(t) of the agents and adaptive gains α i(t) with nodebased protocol (29) and parameters κ1=κ2=1.The states xi(t) converge to the corresponding optimal allocation decisions, and the adaptive gainsαi(t)converge to finite constants.

Fig.4.Case 1: States xi(t) of the agents and adaptive gains a¯k+1,pk(t) with DST-based protocol (5) and parameters κ1=10, κ 2=0.1.A larger κ1 leads to better transient performance of xi(t) and a smaller κ2 leads to smaller steady values of a ¯k+1,pk(t), as compared to Fig.2.

Select κ1=κ2=0.1 for both the DST-based and node-based designs.The states of the agents and the corresponding adaptive gains under (5) and (29) are provided in Figs.5 and 6,respectively.For comparison, let κ2=0, which is the static strategy used in many related works, e.g., [4]–[6].It can be seen from Fig.7 that the resulting nonadaptive strategy fails to solve the resource allocation problem.The reason is that the results in the aforementioned works cannot be adapted to the case with directed communication graphs.

Example 2: In this example, we examine the proposed algorithms applied to the relaxed (i.e., without box constraints)economic dispatch (rED) problem.We consider two benchmark power networks, IEEE 30-bus and IEEE 118-bus, whereNpower generators must cooperatively minimize the cumulative cost, while meeting a total load demandd.In both benchmarks, the cost functions of the generators are of quadratic

Fig.5.Case 2: States xi(t) of the agents and adaptive gains a¯k+1,pk(t) with DST-based protocol (5) and parameters κ 1=κ2=0.1.

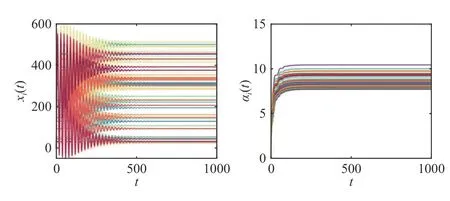
Fig.6.Case 2: States xi(t) of the agents and adaptive gains α i(t) with nodebased protocol (29) and parameters κ 1=κ2=0.1.

Fig.7.Case 2: States xi(t) of the agents with nonadaptive protocol(κ 1=0.1, κ 2=0 in (29)).The states x i(t) diverge.

form:

Two observations follow when comparing our algorithms with the Laplacian-gradient dynamics proposed in [13] for the rED problem: first, in our algorithms the knowledge of the cost functions (or the corresponding gradients) of neighbors is not needed for each generator, which makes our algorithms more privacy-friendly; second, our algorithms are initialization-free (i.e., the initial decisions do not need to satisfy the total load demand).In fact, the initialization-free problem in[13] has also been overcome in [14] by a “dynamic average consensus + Laplacian-gradient” (DAC+LG) algorithm defined as follows:

whereκ1, κ2, α, β ∈R+are tuned based on the Laplacian eigenvalues.Nevertheless, the exchange of the gradients through the network is still needed.Besides, without the adjustable parameter for gradient descent, DAC+LG may suffer from a slower convergence rate (cf.our case study below).

Case 1(IEEE 30-bus):d=103,N=6, G =G1(Fig.1(a));

The power system contains 6 generators.The parameters of the local costs are described in vector form byai=(0.00375,0.0175, 0.0625, 0.00834, 0.025, 0.025)T,bi= (2, 1.75, 1,3.25,3,3)T, andci=0 [42].The power allocation states and the corresponding adaptive gains under (5) and (29) are provided in Figs.8 and 9, respectively, where the dashed lines represent the local optimal power allocation decisions.Meanwhile, Fig.10 shows the simulation result with DAC + LG proposed in [14].

Fig.8.Case 1 (IEEE 30-bus): Power allocation states xi(t) and adaptive gains a ¯k+1,pk(t) with DST-based protocol (5) and parameters κ 1=20 , κ 2=1.

Fig.9.Case 1 (IEEE 30-bus): Power allocation states xi(t) and adaptive gains α i(t) with node-based protocol (29) and parameters κ 1=20 , κ 2=1.

Case 2(IEEE 118-bus):d=105,N=54, G =G2(Fig.1(b));

The power system contains 54 generators.The parameters of the local costs belong to the rangesai∈(0.0024,0.0697),bi∈(8.3391,37.6961), andci∈(6.78,74.33) [41].The power allocation states and the corresponding adaptive gains under(5) and (29) are provided in Figs.11 and 12, respectively,where the dashed lines represent the local optimal power allocation decisions.

When comparing Case 2 to Case 1, one can find that the steady-state gains forN=54 have smaller orders of magnitude as those forN=6.Therefore, we conclude the section by commenting on the lower boundintroduced before (45).Although this bound increases for increasingN, it is only used for stability analysis of algorithm (29), and might be conservative in practice, as discussed in [25], and as evident from our simulations.As a matter of fact, our simulations show that the actual values attained by the adaptive gains are not influenced by the scaleNof the network, but mainly depend on the network structure and the parameter κ2.

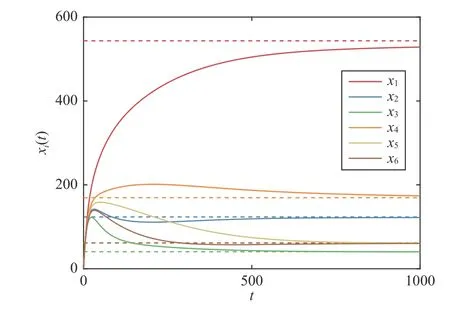
Fig.10.Case 1 (IEEE 30-bus): Power allocation states xi(t) with DAC +LG (46) and parameters κ 1=κ2=1, α =10 , β =60.The parameters are tuned based on the Laplacian eigenvalues [14, Theorem 5.3].

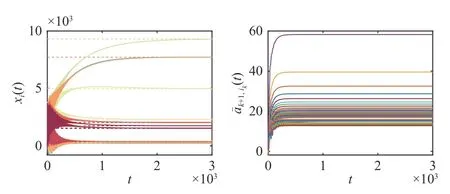
Fig.11.Case2 (IEEE 118-bus): Powerallocation statesxi(t)andadaptive gains a ¯k+1,pk(t)with DST-basedprotocol(5)andparametersκ1=κ2=0.3.

Fig.12.Case 2 (IEEE 118-bus): Power allocation states xi(t) and adaptive gains α i(t) with node-based protocol (29) and parameters κ 1=κ2=0.3.

VI.DISCUSSIONS

[On further comparisons between DST-and node-based algorithms] The DST-based method can in general lead to faster convergence (see Figs.2 and 3 in Section V, and the simulation results in [31] for a distributed optimization problem).This is consistent with intuition since enhancing connections along a DST structure should be more efficient than enhancing connections of all links.Note that a DST structure is known in the literature to be beneficial for cooperative consensus [24], [36].

[On the superiority between DST-and node-based algorithms] Different constraints in real-world applications would decide the superiority between these two algorithms.If faster convergence speed is desired, the DST-based method would be preferable, where the DST structure could be identified via a breadth/depth first algorithm [43, Section 1.4.4] or distributed algorithms [38].If a fully distributed strategy that does not rely on any a priori information is desired, the nodebased algorithm would be preferable, since the DST-based method requires a priori knowledge of a DST structure.

[On the open problems of the DARA algorithms] Note that the Lyapunov functions in (11) and (33) are quadratic.Since results exist where a non-quadratic Lyapunov function may improve performance in adaptive schemes, see e.g., [44],[45], an open future direction is to improve the proposed adaptive resource allocation solutions via non-quadratic Lyapunov functions.Besides, the DARA algorithms in this paper have been formulated for resource allocation problems without local bound constraints.Such local bound constraints may appear in engineering applications such as economic dispatch in the field of power networks.Embedding local bound constraints in the proposed saddle-point dynamics viewpoint is thus a challenge for future work.

VII.CONCLUSIONS

Distributed optimal in-network resource allocation over weight-balanced digraphs was studied.Two novel distributed adaptive saddle-point algorithms named DST-based and nodebased algorithms have been proposed.The asymptotic convergence of each algorithm has been theoretically proved and numerically tested.The proposed adaptive resource allocation frameworks successfully remove the knowledge of the underlying Laplacian eigenvalues, which has been widely used in related literature.Future work includes relaxing the proposed conditions (7) and (30), and studying resource allocation problems with local bound constraints.

ACkNOwLEDGMENT

The first author would like to thank Prof.Jie Mei for the valuable discussions.