基于VMPE的往复压缩机故障诊断方法
2023-12-22李纯思李纯辉
李纯思,李纯辉
(1.哈尔滨千恒鑫仪器设备有限公司,哈尔滨 150000;2.东北石油大学,黑龙江 大庆 163318)
0 引言
往复压缩机作为机械工业中最常用的设备之一,如何准确提取故障特征和故障分类一直都是故障诊断领域研究的热点和难点[1]。由于往复压缩机的振动信号为非平稳非线性信号,传统的线性分析方法难以准确提取其故障特征。随着非线性分析方法研究逐渐成熟,尤其是Shannon将熵的概念引入到信息电子工程领域后,近似熵(AE)、样本熵(SE)、模糊熵(FE)、排列熵(PE)及色散熵(DE)等非线性分析方法被应用到故障诊断领域[2-6]。赵海峰等[7]将近似熵用于测量气阀故障复杂性。张立国等[8]以模糊熵计算后的PR分量为特征向量,表征滚动轴承故障信号的特征信息。冯辅周等[9]将排列熵用于滚动轴承全寿命预测,可显著提前滚动轴承早期故障的检出时间。无论是排列熵还是模糊熵、样本熵都只能描述单一尺度下信号的复杂程度,导致得到的故障信息不完整,因此多尺度样本熵(MSE)、多尺度模糊熵(MFE)、多尺度排列熵(MPE)、多尺度色散熵(MDE)等能够描述不同尺度下信号复杂程度的分析方法被相继提出[10-13]。WU等[14]运用多尺度排列熵提取滚动轴承的故障特征,验证了多尺度排列熵与排列熵相比的优越性。
MPE集合了多尺度熵与排列熵的所有主要优点,无论是在描述序列的完整性上还是相对一致性上均更加优越,且不受数据长短的限制,拥有所需数据短、相对一致性等特点。但MPE在粗粒化计算过程存在以下问题:1)MPE值受尺度因子影响较大,MPE值的稳定性会随着尺度因子的增大而降低;2)在粗粒计算过程中,是基于均值计算粗粒序列,这仅能反映出序列的平均幅值,缺少对信号中波动性的描述。针对这2个问题,本文将方差法代替均值法引入到粗粒化计算中,故本文提出基于方差的多尺度排列熵。最后将VMPE与极限学习机(ELM)相结合,提出一种基于VMPE与ELM的往复压缩机故障诊断方法。试验结果表明,本文所提方法能有效地实现往复压缩机故障诊断,具有较高的故障识别率。
1 VMPE算法
1.1 MPE算法
MPE是将多尺度分析与PE相结合的一种非线性分析方法,用于衡量时间序列在不同尺度下的复杂性和随机性,MPE算法的计算步骤如下。
1)对时间序列{xi,i=1,2,L,N},建立粗粒序列
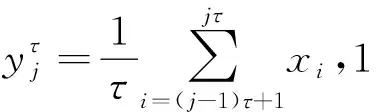
(1)
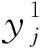
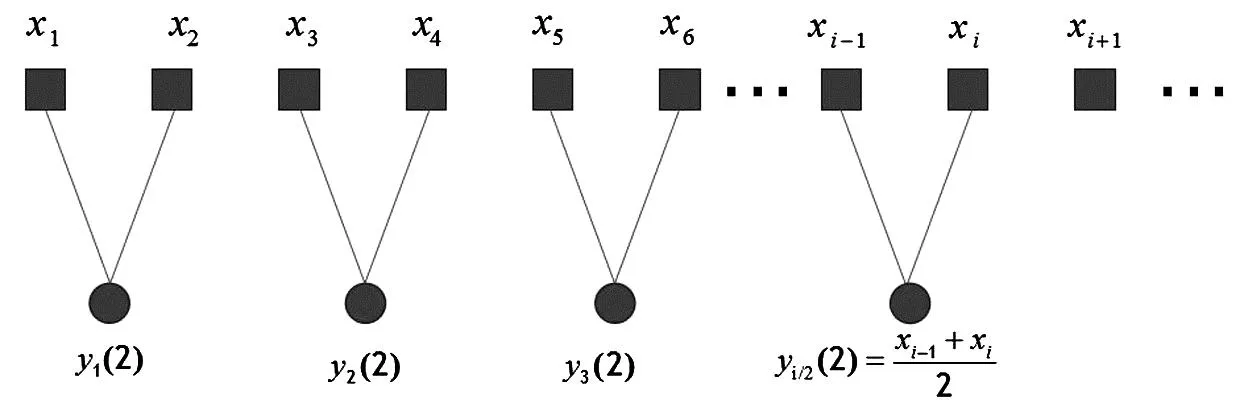
图1 τ=2时粗粒序列计算分割图
由式(1)可看出粗粒化计算过程实质上就是计算数据间的均值,只能反映出序列的平均幅值,忽略了信号中的波动性。
2)分别计算每个尺度下粗粒序列的PE,得到MPE,表达式如下
(2)
式中,m为嵌入维数;t为时间延迟。
1.2 VMPE算法
针对MPE算法存在的问题,将方差法引入到MPE的粗粒化计算中,提出VMPE算法,其具体步骤如下。
1)对时间序列{xi,i=1,2,L,N},建立粗粒序列
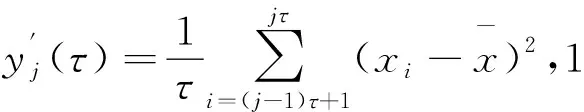
(3)
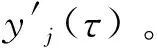
(4)
2 仿真分析
2.1 参数选择
VMPE计算中需设置四个参数,尺度因子τ、嵌入维数m、时间延迟t、时间序列长度N。
1)对于尺度因子τ,为了保证粗粒序列的长度不能过短,所以τ的选择不能过大,一般情况下取τmax≥10,本文取τmax=20。
2)排列熵对嵌入维数m的依赖性较大,m取值越大,序列需要重构的信息越多,序列的细微变化越容易被忽略[15];m取值越小,重构信号的维度越低,包含着状态越少,序列的动态变化难以检测,Bandt建议嵌入维数m在3~7间选取[5],本文取m=6。
3)经众多学者对排列熵的研究表明,时间延迟t的选取对结果几乎没有影响,本文取t=1。
4)对于时间序列长度N,无论是长度选取过长或者过短都会对熵值产生较大的影响,根据文献[16]研究,建议N的选取需大于3 000。
2.2 仿真对比分析
结合上一小节中对VMPE中各项参数的分析,为说明VMPE方法的优越性,以数据长度为4 000的高斯白噪声为研究对象,选择m=6、t=1,计算20个尺度下的MPE和VMPE,结果如图3所示。从图3中可以看出,MPE与VMPE相比,熵值曲线明显光滑性更差,说明被方差法改进后的MPE在处理信号时,能保留更多有用的信息。VMPE熵值曲线的熵值波动更小,尤其在高尺度段两种方法的波动性差异较明显,整体来看,VMPE熵值曲线更光滑,说明与MPE相比,VMPE更优越,稳定性更好。
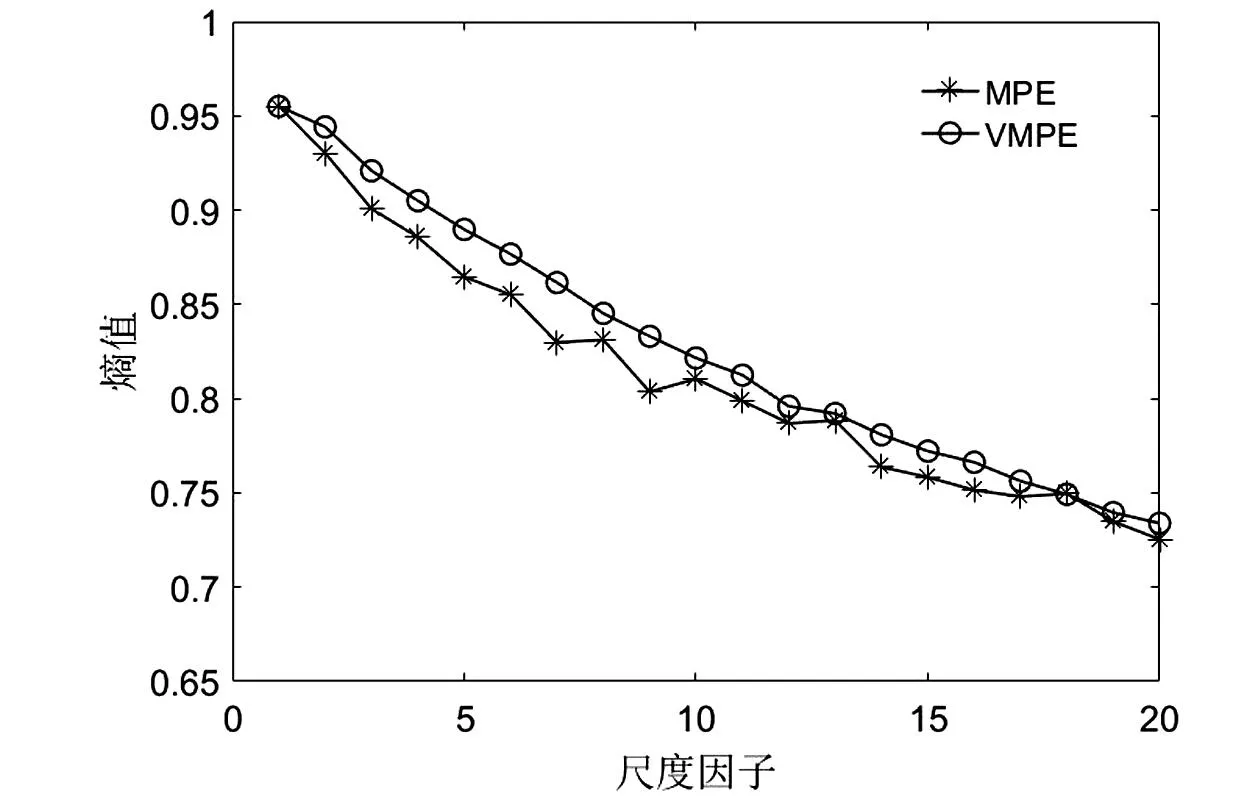
图3 高斯白噪声的VMPE和MPE值
3 基于VMPE和ELM往复压缩机故障诊断方法
3.1 滚动轴承故障诊断流程
通过前面章节的分析,提出基于VMPE和ELM往复压缩机中滚动轴承故障诊断方法。具体诊断步骤如下。
1)设置k种气阀故障状态,每种状态采集n个样本,对所有样本计算在τ个尺度下的VMPE,选取合适数量的VMPE值作为特征向量。
2)在每种状态下随机抽取i个作为分类器的训练样本,组成训练集,剩余n-i作为测试样本组成的测试集。
3)将训练集中每个状态的特征向量输入到ELM中训练,得到ELM训练模型,然后将测试集中的特征向量输入到ELM中进行测试。
4)根据ELM分类器的输出结果实现滚动轴承故障诊断。
3.2 气阀故障实例分析
为了验证本文方法在实际工况下的适用性和优越性,对2D12型往复压缩机的气阀故障进行研究,模拟了弹簧失效、阀片断裂和阀片缺口3种常见故障,使用加速度传感器在采样频率为50 kHz的工况下采集正常、弹簧失效、阀片断裂和阀片缺口4种情况。每种状态取30个样本,每个样本有4 096个数据点,其中10个样本作为训练集,另外20个样本作为测试集,滚动轴承的试验数据详细描述如表1所示,4种状态的时域波形如图4所示。
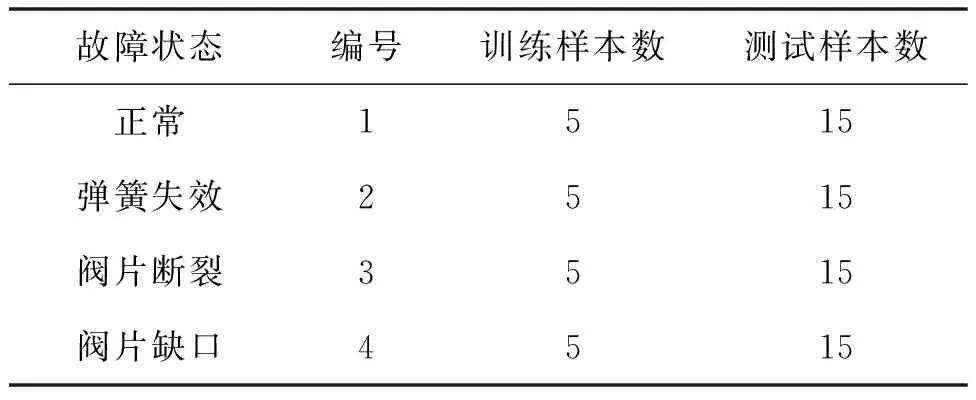
表1 训练和测试实验数据列表

图4 气阀4种状态振动信号的时域波形图
在嵌入维数m=6,时间延拓t=1的参数条件下,对所有样本计算在20个尺度下MPE和VMPE,4种状态的MPE和VMPE结果如图5和图6所示。从图5和图6中可以看出,4种状态熵值曲线的整体趋势大致相同,VMPE与MPE相比,明显熵值波动性更小,说明VMPE稳定性更好。

图5 4种气阀状态的VMPE图
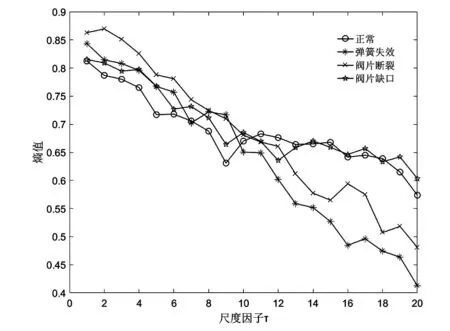
图6 4种气阀状态的MPE图
为了准确的评估气阀的故障状态,引入ELM识别4种状态。首先,将每种状态的20个VMPE特征样本,选取5个作为分类器的训练样本,组成训练集,剩余15个作为测试样本,组成测试集。其中,ELM激活函数选取Sigmoid函数[17],隐层神经元的数目设置为25;然后,将训练样本输入到ELM中进行训练;最后,将测试样本输入到训练好的ELM中进行识别,结果如图7所示。由图7可以看出,实际的输出结果与理论结果完全相同,故障识别率为100%(60/60),说明本文所提方法能有效地识别往复压缩机的故障状态。
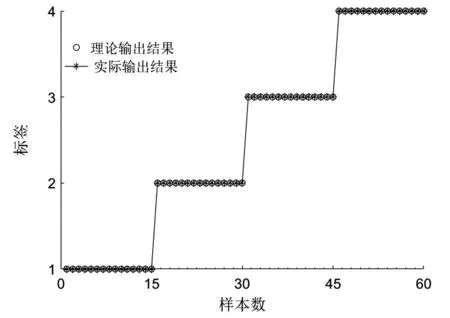
图7 基于VMPE和ELM的识别结果
将每种状态的20个样本经基于MPE和ELM的方法进行特征提取,在相同的训练样本数和测试样本数下,输入到ELM分类器中训练和测试,故障识别结果如表2所示。从表2中可以看出,基于VMPE和ELM的方法在所有状态下都未出现错分,而基于MPE和ELM的方法出现错误识别。表明基于VMPE和ELM的故障识别方法无论是在整体上还是个别状态的识别率均优于基于MPE和ELM,验证了其在气阀故障诊断上的优越性。
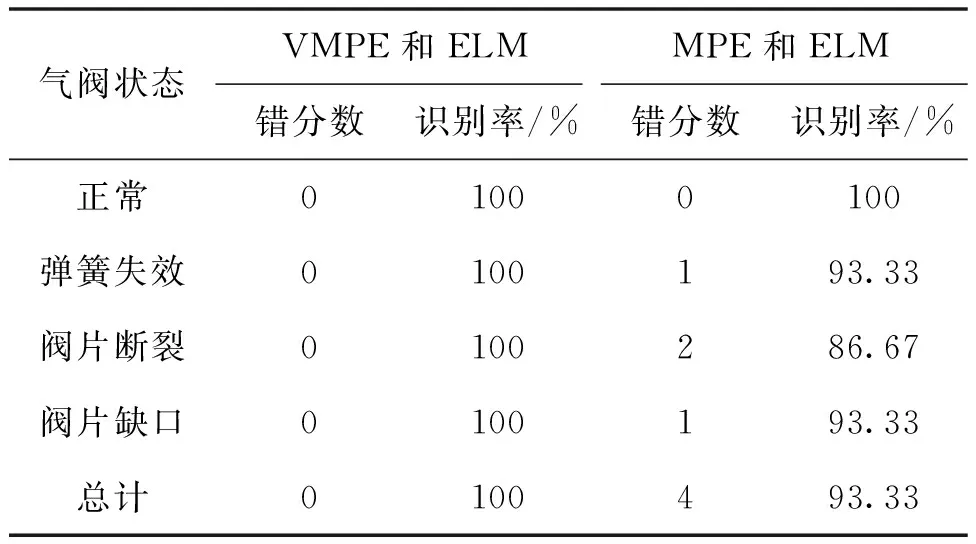
表2 两种方法的故障识别结果
4 结论
本文在MPE的基础上,提出了VMPE来衡量非线性时间序列的复杂程度,对粗粒化序列进行了优化。通过对高斯白噪声信号的分析,验证了其与MPE相比,在特征提取方面的优越性。
在研究VMPE特征提取方法和ELM的基础上,提出了一种新的往复压缩机故障诊断方法,并对2D12型往复压缩机气阀故障试验案例进行了分析。将VMPE与MPE进行了对比,验证VMPE的稳定性优于MPE,基于VMPE和ELM的往复压缩机故障诊断方法比基于MPE和ELM方法的故障识别率更高。
