变角度混杂复合材料层合板振动特性研究

2023-12-22彭运松罗兴宇李想张浩天张晨旭段少华

当代化工研究 2023年21期

＊彭运松罗兴宇李想张浩天张晨旭段少华

（1.中船第七二五所河南 471000 2.南京航空航天大学材料科学与技术学院江苏 210000）

复合材料层压板具有比强度高、比重量轻、比刚度大、抗疲劳性能好等优点[1-3]，目前已经成为一类重要的工程结构件，广泛应用于船舶、铁路、航空、机械工程和机器人等领域。胶合板材料常用于制作薄壁轻质结构，如层压板、夹芯板和增强板。薄壁结构在外部条件下容易受到高振动和几何非线性的影响，从而引起结构的面外振动破坏。基于目前的研究现状，国内外研究人员在复合材料层压结构动力特性方面取得了诸多成果。

Leena Sinha[4]采用FFT（Fast Fourier Transform）分析仪，针对有/无孔层合板，采用不同的长径比、层数、增强纤维与树脂的比例、纤维取向等因素，分别对有/无孔层合板的自振特性进行了分析和数值模拟。杜霖[5]研究表明，在平直铺层中引入变角铺层可以有效地提高叠层板面内失稳荷载。郑天禄[6]以单一纤维的阻尼特性为基础，对三种混合纤维材料进行了流-固耦合数值模拟。李亮等[7]利用自动铺展模制技术，对变刚度层合结构的振动特征进行了研究，发现：在共振峰值处，TF和起始点的加速度总方根（RMS）相比较，纤维夹角的变化对共振峰值的阻尼效果有明显的影响。曾令旗等[8]制备了玻/碳纤维复合层合板，并采用ANSYS对其在层间和夹芯两种混合模式下的振动特征进行了分析，结果表明：夹芯混合层的自振频率大于层间，且自振频率随厚度增加而增大。

目前，复合材料的振动响应主要集中在传统的线性层上，近年来，采用变刚度分层结构作为一种新型减振方法，为减振降噪提供了新的设计理念和性能优化方法[9-10]。因此在传统直线层合板中引入了纤维曲线铺层，一方面改善了层合板的固有频率，对阻尼减振起了重要的作用，另一方面在保证了自身的刚度的前提下降低了重量。

1.实验材料及设备

(1)实验材料

层合板类型分别为1块8层纯碳纤维直线铺层层合板、4块14层混杂纤维直线铺层层合板、5块8层纯碳纤维曲线铺层层合板、5块8层纤维混杂曲线铺层层合板，曲线纤维角度的变化梯度为15°，混杂比为14.3%、28.6%、42.9%、50%，混杂方式为夹芯混杂。

(2)实验设备

实验采用DH5922D振动数据采集设备，所用软件为DHDAS动态信号测试分析系统，分析点数为1024，采样频率为512Hz，力锤敲击平均次数设置为3次，力锤灵敏度设为2mV/N，力锤量程选择为48N，加速度传感器灵敏度为5mV/(m·s-2)，力锤量程为40m/s2，输入方式为IEPE，实验仪器详见表1。

表1 模态实验设备型号

2.实验方案

(1)实验模态分析理论基础

模态分析通过对结构刚度、质量、极限状态等多个自由度分析来研究结构动态特性。模态分析不依赖于外界激励情况，对试件振动信号与响应进行分析，并对其进行模态辨识，从而获得内部频率、阻尼比及其它模态特征[11]。

当外界的瞬时形态的干扰发生时，结构体系会自然而然地以某一固定频率发生振动，这一频率被称作结构固有频率，是一种与外界激励无关的自振频率[12]。

式中，ωd是含有阻尼的固有频率；ζ为系统的阻尼比，一般体系的阻尼比都在10%以下。一般当系统结构发生振动时，其对应的频响函数的基本公式可以表示为：

式中，Xi(ω)表示在点i处的系统速度响应经过傅利叶变换后在ω频率处的强度值；Fj(ω)为第j点经过傅利叶变换后在频率ω处的强度值。

(2)模态实验方案

实验前，需要在层合板的X轴上测量出30mm的夹持距离，随后在270mm×300mm的层合板上均匀划分9个激振点，由于加速度传感器易受电流和重量的影响，因此测量设备需一端接地，采用0.05mm×8mm×8mm的胶板固定传感器，通过力锤逐点敲击激励点获得层合板的前三阶的固有频率、振型和阻尼比。

图1 力锤实验法实验装置

①在进行力锤法敲击实验前，在层合板X轴方向标注30mm的夹持线，并均匀划分9个激励点，选取5号点为层合板的拾振点，并在5号点处粘贴垫片。

图2 层合板测点布置

②将模态数据采集仪通过网线连接计算机，并在模态分析软件中建立层合板模态模型，并布置测点号。

图3 层合板模态模型建立示意图

图4 固支状态夹持装置

③将层合板沿着夹持尺寸固定在夹持底座上，此时层合板呈现固支状态。

④将加速度传感器的连接模态数据采集仪的第二通道，另一头粘贴在层合板的5号测点处。

⑤将力锤连接模态数据采集仪的第一通道，对层合板各拾振点逐点激励，每个激励点敲击3次，若响应信号幅值过大或过小，应选择重新敲击。

⑥在模态分析软件中进行频段选择，将数据采集的频响信号进行极值点标注，然后进行稳态图计算，最后通过模态模块得到每块层板的频率响应函数、振型和阻尼比。

3.模态实验结果及参数分析

(1)不同角度铺层层合板模态分析

根据上述实验过程，依次对5块纯CF曲线铺层层合板进行模态分析后得到对应的频响函数图，如图6所示。

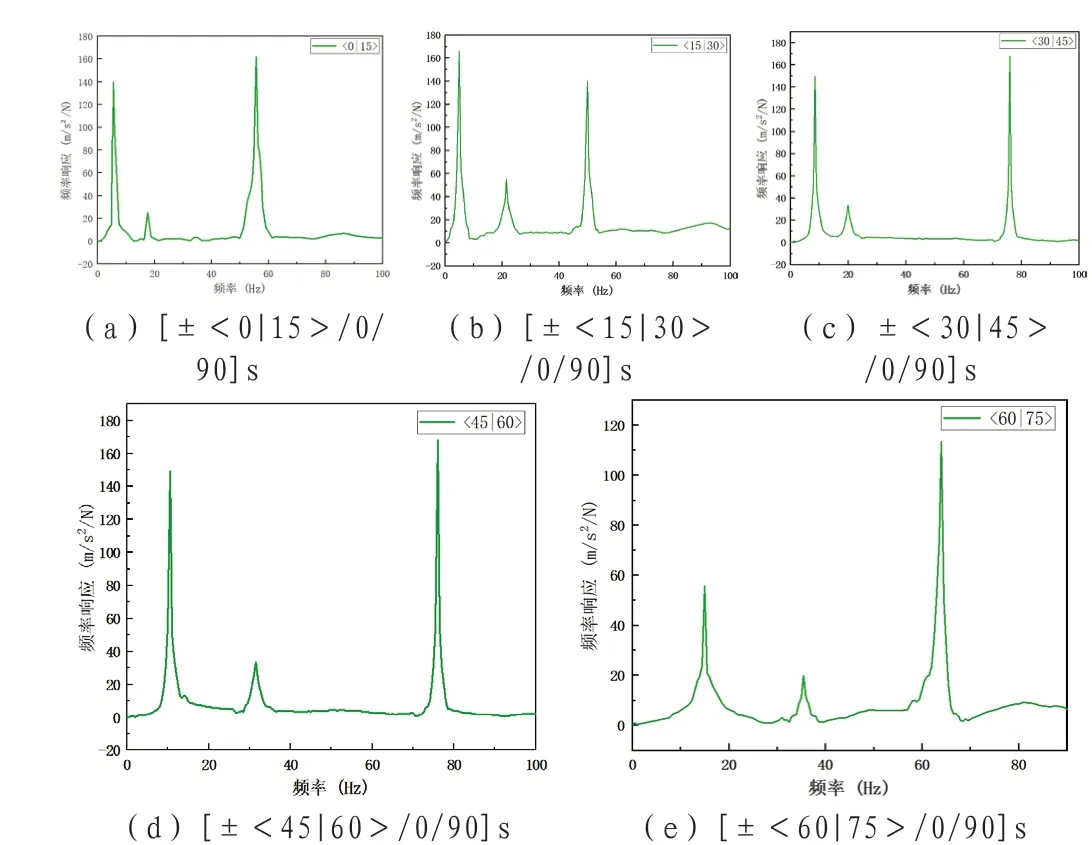
图6 纯CF曲线铺层层合板频响函数图

表2为根据频响函数拟合计算得到的模态参数，包括前三阶的固有频率和前三阶阻尼参数。由表可以看出随着CF纤维角度变化，一阶固有频率随着纤维角度的增加而递增，±＜60|75＞相比于±＜0|15＞的固有频率提高了168%。当铺层顺序为[±＜60|75＞/0/90]s二阶固有频率最大为36.05Hz，相比于其他变角度铺层最多提高了111%。当铺层顺序为[±＜30|45＞/0/90]s三阶固有频率最大为76.53Hz，相比于其他变角度铺层最多提高了37%。

表2 8层纯CF（CARBON FIBRE）曲线铺层层合板模态参数结果

从表2中可以观察到各阶模态参数随着纤维角度的变化呈非线性变化，从整体看，纤维角度的变化对一阶固有频率影响最为显著，固有频率随着纤维角度增加而增加，三阶固有频率相对来说影响较小，固有频率随着纤维角度增加呈现先增加后减少的趋势。一阶阻尼比变化较平缓，均在0.9%左右，高阶模态参数有所提升主要是由于高阶弯曲扭转变形受刚度影响更大，在[±＜45|60＞/0/90]s综合模态参数最优。

(2)不同混杂比铺层层合板模态分析

图7为5块混杂曲线铺层层合板进行模态分析后得到频响函数图。

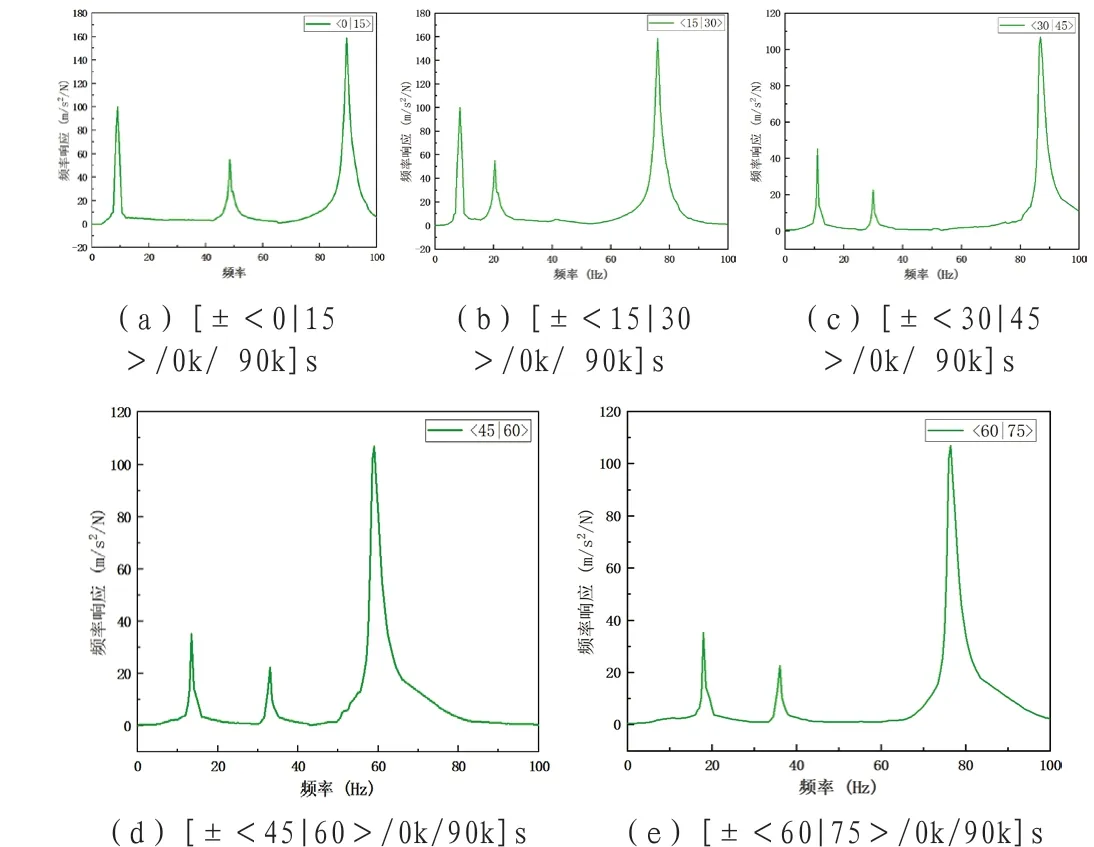
图7 混杂曲线铺层层合板频响函数图

表3 8层混杂曲线铺层层合板模态参数结果

根据混杂曲线铺层层合板固有频率和阻尼比的变化趋势，可以发现一阶固有频率和纯CF曲线铺层层合板相似，随着纤维角度变化的增大，层合板的一阶固有频率增大，但二阶和三阶固有频率在加入Kevlar阻尼插层后，呈现出W形变化。随着纤维夹角度的增加，复合材料的一阶阻尼比表现出先上升后下降的趋势，这说明纤维夹角可以使复合材料层合板的中段产生更大的弯曲变形，从而使复合材料的模态特性得到极大的改善。从总体上来看，在层合板的设计阶段，在满足力学性能要求的情况下，选择最优的铺层序列模态参数[±＜45|60＞/0k/90k]s，可以得到较好的振动特征和阻尼性能。