气体波动引起的弯曲流道气波机振荡管结构动态响应研究*
2023-12-20张博旭王泽武
尹 彬,张博旭,王泽武
(大连理工大学 化工机械与安全系,辽宁 大连 116024)
0 引 言
气波制冷机是利用气体的压力能产生激波和膨胀波进行制冷的一种特殊设备,在石油化工[1]、航空航天[2]及食品速冻保鲜[3]等领域得到了广泛应用。
近年来,胡大鹏等人[4-7]创新性地提出了外循环耗散式双开口气波机,解决了传统气波机热能难以回收和积液的问题,使制冷综合效率得到显著提升。代玉强等人[8-13]研究了直流道气波机结构和操作参数对双开口气波机制冷性能的影响;然而直流道气波机同时也存在较大的非等熵流动损失。为此,赵一鸣等人[14]进一步提出了弯曲流道双开口气波机,该气波机既有利于减小高压射气损失,又可降低中压端口内的气体流动损失,降低热端能量耗散,因此可显著改善气波机的工作性能。在弯曲角度设计参考工况下,各性能参数相对直流道的提升比例可达到25.3%。
波转子是气波机的核心工作部件,其振荡管间插片厚度通常小于2 mm,且越薄越有利于提升气波制冷机的制冷效率;但是插片也是气波机中最为薄弱的元件,容易损坏而引发事故。吴响响等人[15-16]对直流道气波机振荡管内流场和波转子模态进行了研究,得到了振荡管内非定常流体激振力下插片元件的结构动态响应;但是,目前鲜有针对弯曲流道气波机插片元件在流体流动诱导下动态响应的研究。
此外,为了研究流致振动问题,多场耦合技术在流体机械、输流管道和航空航天等领域得到了广泛应用[17-26]。
为研究弯曲流道气波机在非定常高频高压流体激励载荷作用下能否安全运行,笔者提出采用多物理场耦合方法,开发弯曲流道双开口气波机三维流固耦合数值计算模型,研究振荡管内的非定常流场流动特性,进而提取复杂波动引起的流激力;然后,进行振荡管插片元件结构动态响应分析和波转子固有频率分析;最终,判断结构改进是否会引起气波机不安全运行行为。
1 弯曲流道气波机三维流固耦合模型
1.1 模型简化
气波机波转子三维模型如图1所示。

图1 气波机波转子三维模型Fig.1 Three-dimensional model of wave rotor in the gas-wave refrigerator
图1为双开口气波机波转子,波转子主要由内外筒、插片及密封元件组成。内、外筒体与插片组成横截面近似长方形孔的72根振荡管,圆周方向两根相邻振荡管共用一根插片。
气波机通过各进出气口、波转子与旋转轴相连,并置于机壳内。为防止动、静部件摩擦,其进出气口与波转子两端设有微小间隙,一般要求间隙低于0.2 mm。
为确保波转子变形在可控范围之内,设计前需要精确计算波转子在转动过程中的变形量。
其他双开口气波机相关参数如表1所示。

表1 双开口气波机结构参数
振荡管内气体流动状态复杂,网格数量、流固耦合数据交换、刚度矩阵求解等均会消耗大量计算资源,因此进行合理的模型简化十分必要。
考虑到波转子的振荡管呈周期性分布,笔者从72根振荡管取出7根振荡管进行分析,中间5根管参与流固耦合主计算,外侧两根振荡管作为支撑以防止内、外圆筒发生过大变形。
简化后的模型不仅能够准确模拟固壁反射、相邻振荡管端部之间的相互影响,而且还大大降低了计算规模。
流体域模型和对应结构域模型如图2所示。
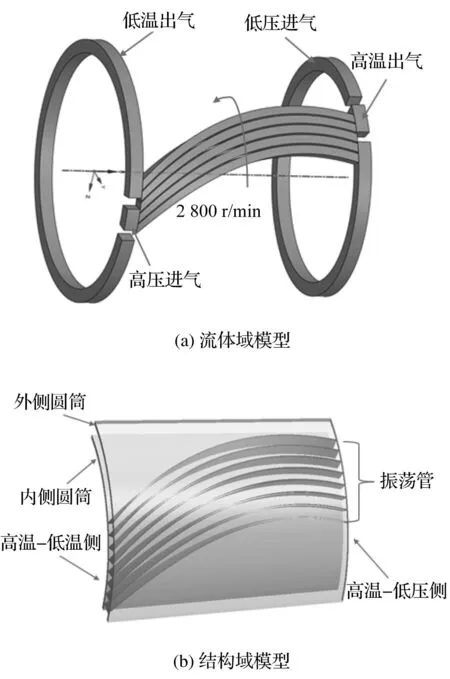
图2 气波机波转子三维简化模型Fig.2 Simplified three-dimensional model of wave rotor in the gas-wave refrigerator
1.2 三维数值模型开发与可靠性验证
气波机三维流体模型边界条件有以下5种:
“压力进口”边界条件包括高压进气口和低压进气口;“压力出口”边界条件包括高温出气口和低温出气口;两对“滑移边界”边界条件包括振荡管内流体左端和高压入口、低温出口右端的接触面、振荡管内流体右端和高温出口、低压入口左端的接触面;振荡管内部流体默认为“内部”,流固耦合面均设置为壁面。
该弯曲流道气波机工况压比(PHP/PHT)为4。
4个进出气口的压力、温度和水力直径数据如表2所示。
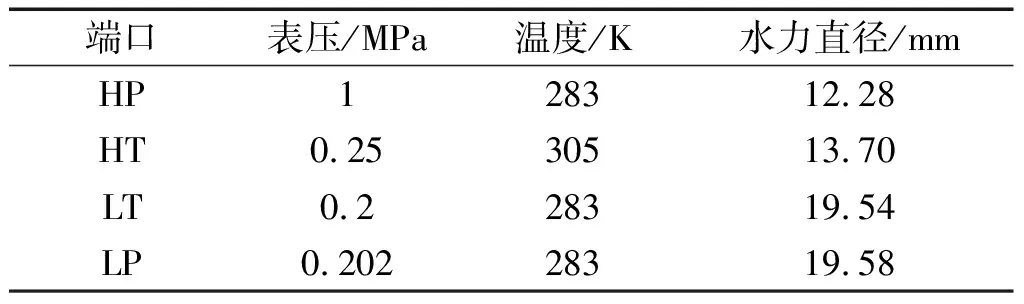
表2 双开口气波机进、出气端口边界条件
工程应用领域中,对湍流流动的模拟主要以RANS方法为主。在Fluent的相关设置中,笔者选择k-ωSST模型作为湍流模型,把振荡管和各进出气口内气体视为理想气体,网格交界面按滑移边界将各端面匹配,计算前根据表2为各进出气口内流体设置初值。
在Transient Structural模块中,笔者为固体域模型赋予不锈钢金属材料,流场稳定后,多周期流固耦合结果仅为单周期流固耦合的近似重复。
由于流固耦合计算对计算资源需求极高,因此,笔者根据流体域结果匹配数据量和时间步长,进行一个旋转周期的流固耦合计算。
由于气波机波转子刚度大,其结构变形对流体流动影响甚微。因此,为提高计算效率,笔者选用单向流固耦合方法。流体域采用多区域网格划分方法,以六面体结构化网格为主。
为准确计算插片附近流场分布与激励载荷波动,笔者在进出气口和振荡管流体域壁面设置了一定的初始厚度和增长率的膨胀层。
接下来需要进行网格无关性和时间独立性验证。笔者设置网格尺寸分别为0.5 mm、0.75 mm、1 mm、1.5 mm和2 mm,时间步长分别为1×10-6s、5×10-6s、1×10-5s、2×10-5s和5×10-5s;以网格尺寸和时间步长分别作为自变量,中间振荡管所受力矩作为变量,将力矩值在不同网格数和不同时间步长下进行连线,得到可靠性验证结果,如图3所示。
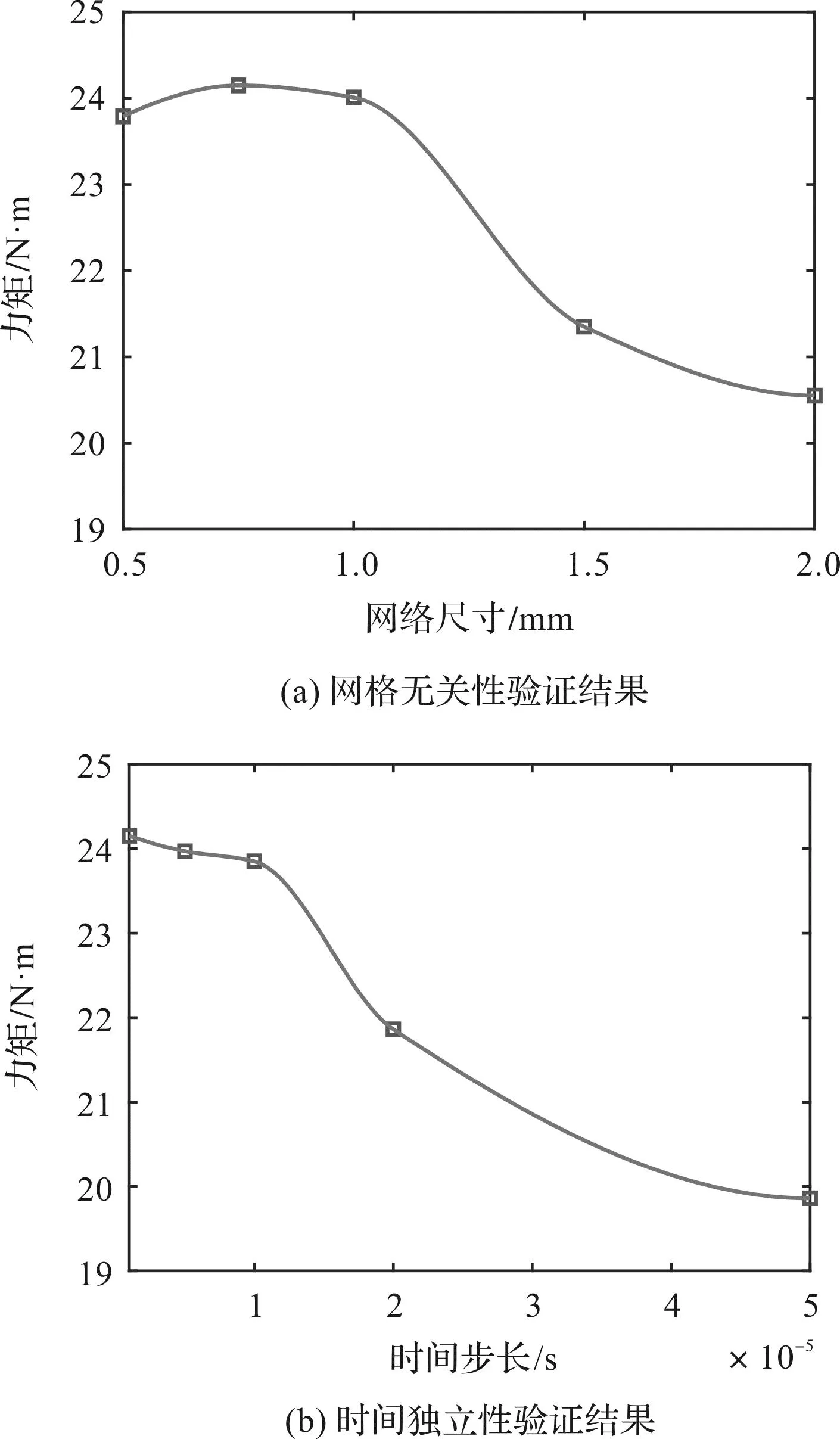
图3 可靠性验证Fig.3 Reliability verification
当网格尺寸小于等于1 mm,时间步长小于等于1×10-5s时,中间振荡管所受的力矩变化不大,说明1 mm的网格尺寸已达到网格无关,时间步长取1×10-5s可保证计算速度和精度。
气波机波转子的转速为2 800 r/min。为更好地捕捉管内激波、压缩波和膨胀波,笔者设置总时间步为15 000步,波转子共旋转约7圈。
为保证流固耦合计算的准确性,笔者设置波转子插片网格尺寸与流体域一致,内外筒网格尺寸为2 mm,最终得到波转子数值计算网格模型,如图4所示。
2 弯曲流道振荡管流场特性分析
2.1 压力场分布
弯曲流道气波机振荡管插片结构动态响应主要由振荡管内流体压力场波动引起。
为了研究振荡管内压力场随波转子旋转的波动特性,笔者绘制出5根振荡管高压进气和低温排气阶段的压力分布云图,如图5所示。
由图5(a)可知:在高压进气阶段,振荡管与高压入口接通,高压气体入射振荡管并产生激波,随着时间推移激波逐渐向右侧高温出口传播,经过之处压力升高,振荡管内压力波动剧烈。
从图5(b)可知:低温排气阶段振荡管与低温出口接通,管内压力场较为平稳。振荡管端口与固壁接触时产生膨胀波,膨胀波使管内压力降低。弯曲流道气波机波转子压力在0.069 4 MPa~1.141 0 MPa的范围内波动,波转子旋转,振荡管两侧端口随着历经与各出入口接通和断开的过程。
振荡管与高压入口接通时,管内压力较大且波动剧烈;与低压入口接通时,管内压力较小且分布均匀;当振荡管左端口与高压入口完全接通时,靠近高压入口端管内的局部压力比高压入口的入射压力1 MPa高出14.1%,并且该位置两侧压力梯度很大。
振荡管与高压入口和高温出口的渐开渐闭过程所引起的气体波动行为较为复杂,振荡管内压力随着波转子转动而呈周期性分布,压力较大值主要集中在靠近高压的入口侧。
2.2 激励载荷的提取与分析
振荡管内高频波动的非定常压力场是引起振荡管插片振动的主要激励源。因此,对波转子振荡管插片所受激励载荷进行分析是掌握气波机振荡管振动特性的基础。
由图5(a)可知:振荡管与高压入口接通处的压力较为集中,管内压力存在强间断。因此,笔者选取具有代表性的中间振荡管迎风侧第1、第7节点,以提取压力载荷。
迎风侧第1、第7节点位置与压力-时间曲线如图6所示。
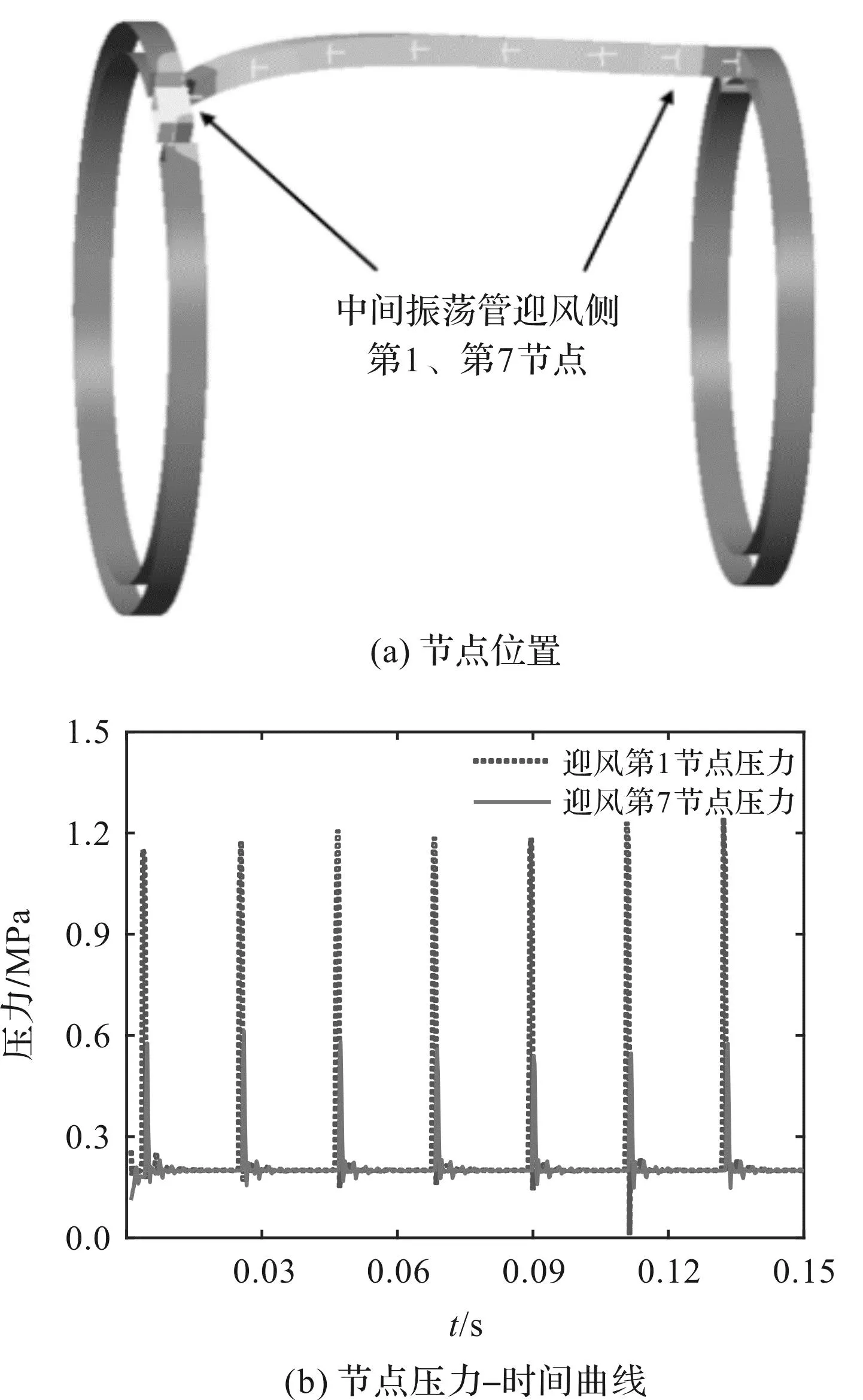
图6 迎风侧第1、第7节点位置与压力-时间曲线Fig.6 Position and pressure-time curves of the first and seventh nodes on the windward side
由图6(b)可知:第1周期数据在波峰前有波动,与后续数据呈现的规律存在较大差异,因此,需要舍弃第1周期数据。
迎风侧第1、第7两个节点压力峰值分别为1.179 MPa和0.559 5 MPa,第7节点压力峰值时间较第1节点延后0.006 s;两点压力均呈现快速的先上升后震荡衰减的趋势,到下一个周期重复该规律,第1节点压力衰减速度快于第7节点。
第5周期第1节点迎风侧和背风侧压力与压差曲线,如图7所示。
由图7(a)可知:迎风侧第1节点压力从最大值到最小值仅用时0.000 4 s,背风侧压力波动较小;迎风侧比背风侧早0.000 2 s到达最大值,早0.000 4 s到达最小值。
由图7(b)可知:在振荡管同一位置处,迎风侧与背风侧压力存在一定的差值,大约在-0.185 6 MPa~0.971 2 MPa之间,振荡管插片同时受左右两侧压力作用;正向压力主要受迎风侧作用,背向压力受二者共同作用(这样复杂的压力波动会引起振荡管不期望的振动,从而降低气波机振荡管的疲劳寿命,尤其是在插片更薄时)。
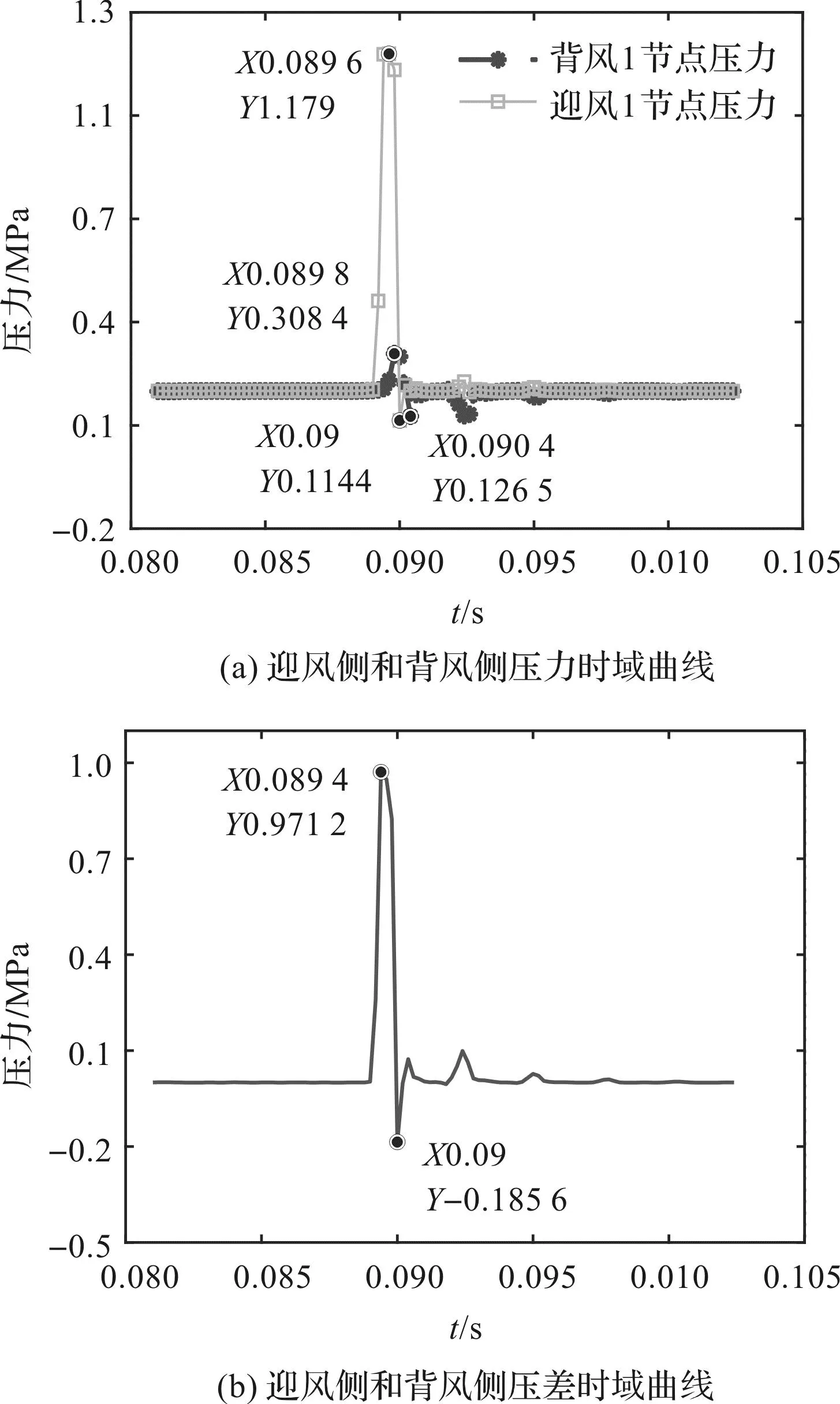
图7 第5周期第1节点迎风侧和背风侧压力与压差曲线Fig.7 Pressure and pressure difference curves of the windward side and leeward side of the first node incycle 5
3 振荡管结构动态响应及模态分析
3.1 位移场分析
笔者选取流场计算第5周期的压力载荷数据,利用Workbench流固耦合平台,导入Transient Structural模块,进行振荡管结构强度的瞬态计算。
为了直观表示弯曲流道振荡管的位移场分布,以及不同时刻、不同位置的位移动态变化规律,笔者绘制了中间振荡管迎风侧插片位移云图和中间振荡管迎风侧插片中线的位移-时间-位置三维曲线,如图8所示。
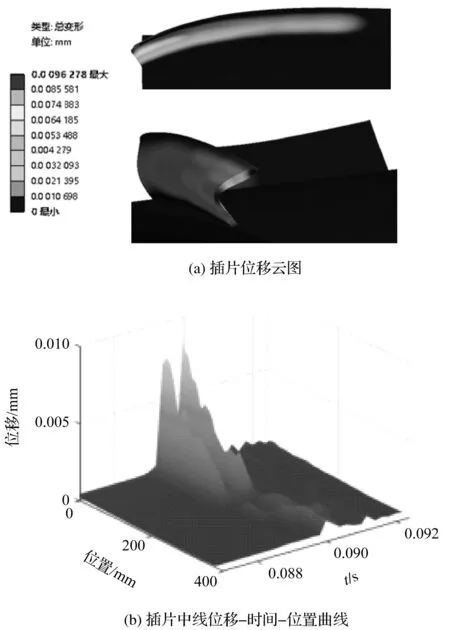
图8 弯曲流道振荡管迎风侧插片位移场Fig.8 Displacement field of the windward side insert of the oscillating tube with curved channel
为了便于研究振荡管插片最大位移节点的位移变化规律,笔者绘制迎风侧第1节点位移-时间曲线,如图9所示。
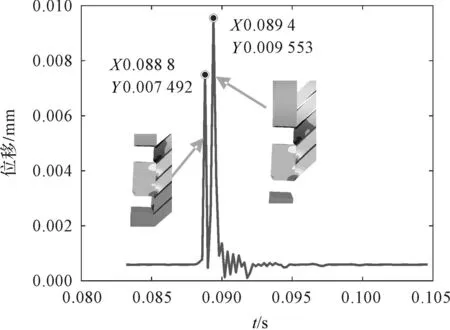
图9 迎风侧插片第1节点位移-时间曲线Fig.9 Displacement-time curve of the first node of the windward side insert
由图8(a)可知:弯曲流道振荡管最大位移发生在高压入口处的插片中间位置,最大位移为0.009 6 mm。
图8(b)中的两个峰值表明,振荡管位移幅值同时受左右两侧压力的影响,在整个周期内靠近高温出口处均未发生明显变形。
由图9可知:中间振荡管迎风侧插片的最大位移发生在0.089 4 s时刻,此时振荡管刚好与高压入口完全分离,而后一根振荡管与高压入口尚未分离;次大位移发生在0.088 8 s时刻,中间振荡管刚与高压入口完全接通,后一个振荡管尚未与高压入口接通。当振荡管与低压入口接通时,插片位位移仅有小幅波动。
在非定常流体激励载荷作用下,弯曲流道气波机振荡管插片会产生轴向位移,可能导致波转子与进出气口发生动静部件摩擦。为此,笔者调取了振荡管插片轴向位移最大时刻的位移云图,如图10所示。
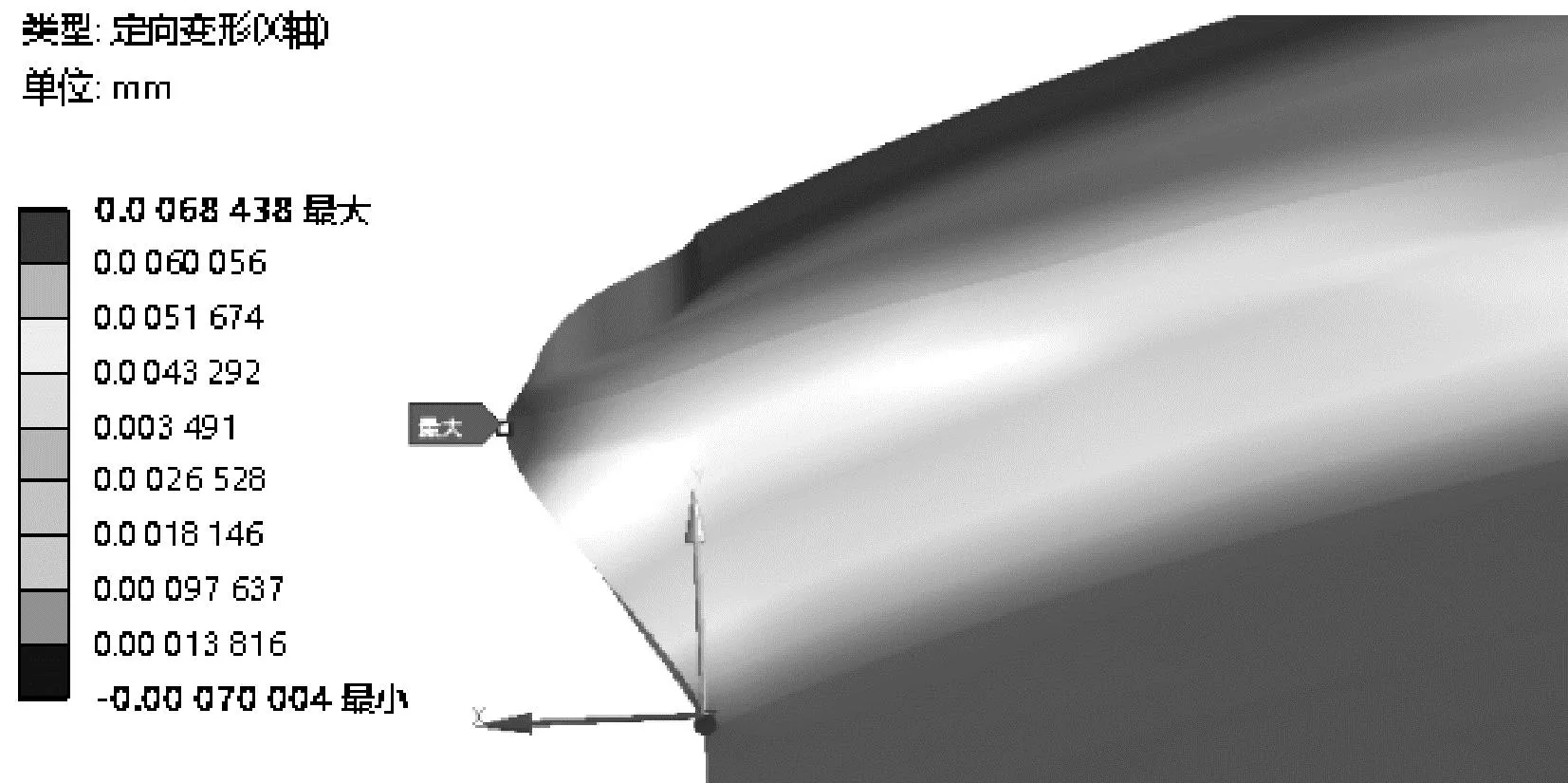
图10 振荡管插片最大轴向位移云图Fig.10 Cloud image of the maximum axial displacement of the oscillating tube insert
由图10可知:振荡管插片最大轴向位移为0.006 8 mm,小于设计要求的0.2 mm,由此可以判断,波转子与进出气口不会发生动静部件摩擦。
3.2 应力场分析
为判断振荡管插片是否会发生强度失效,以及直观表示振荡管不同时刻、不同位置的应力动态分布,笔者绘制弯曲流道中间振荡管迎风侧插片应力场云图和插片中线应力-时间-位置曲线如图11所示。
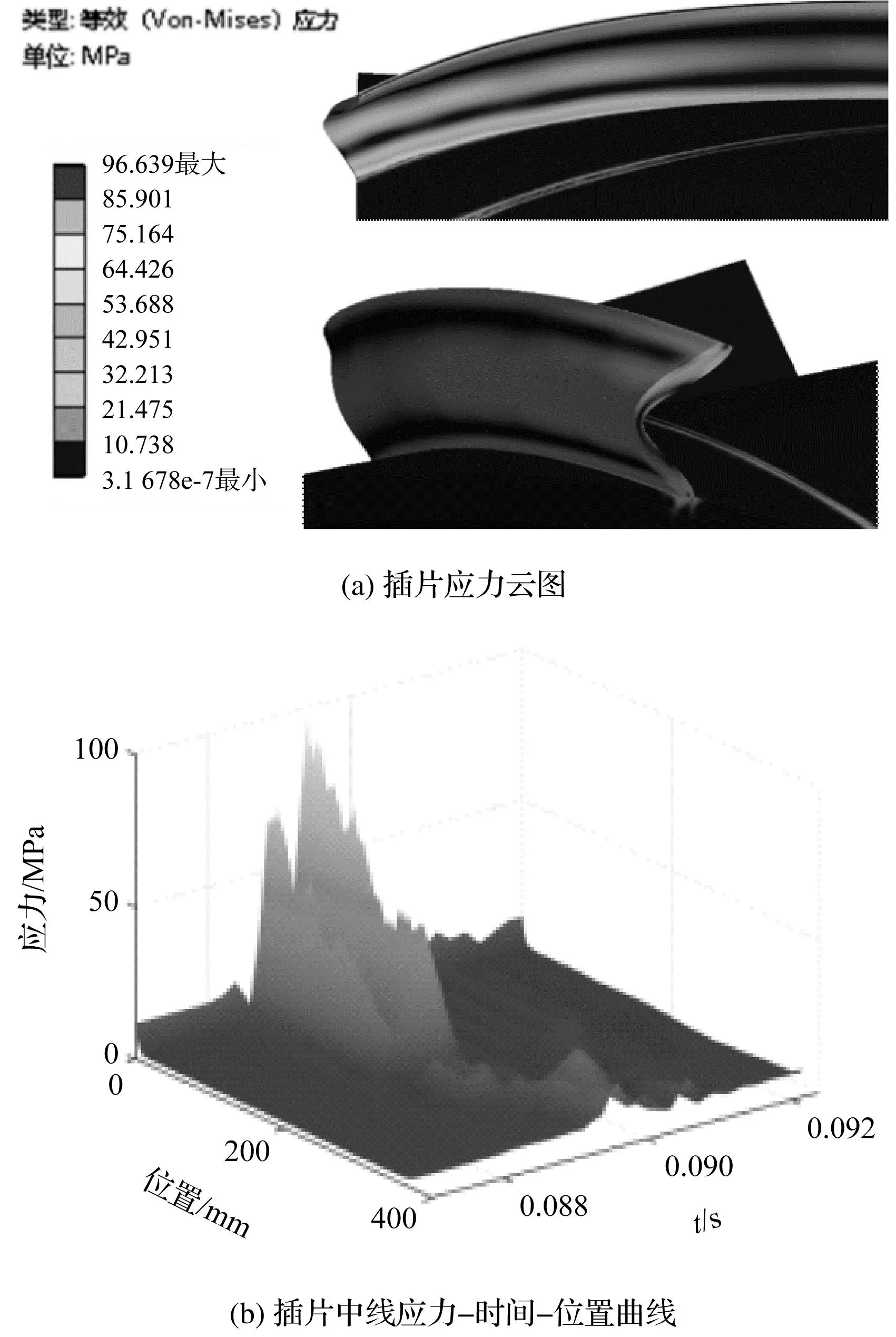
图11 弯曲流道振荡管迎风侧插片应力场Fig.11 Stress field of windward side insert of oscillating tube with curved channel
笔者绘制插片第1节点应力时域曲线如图12所示。
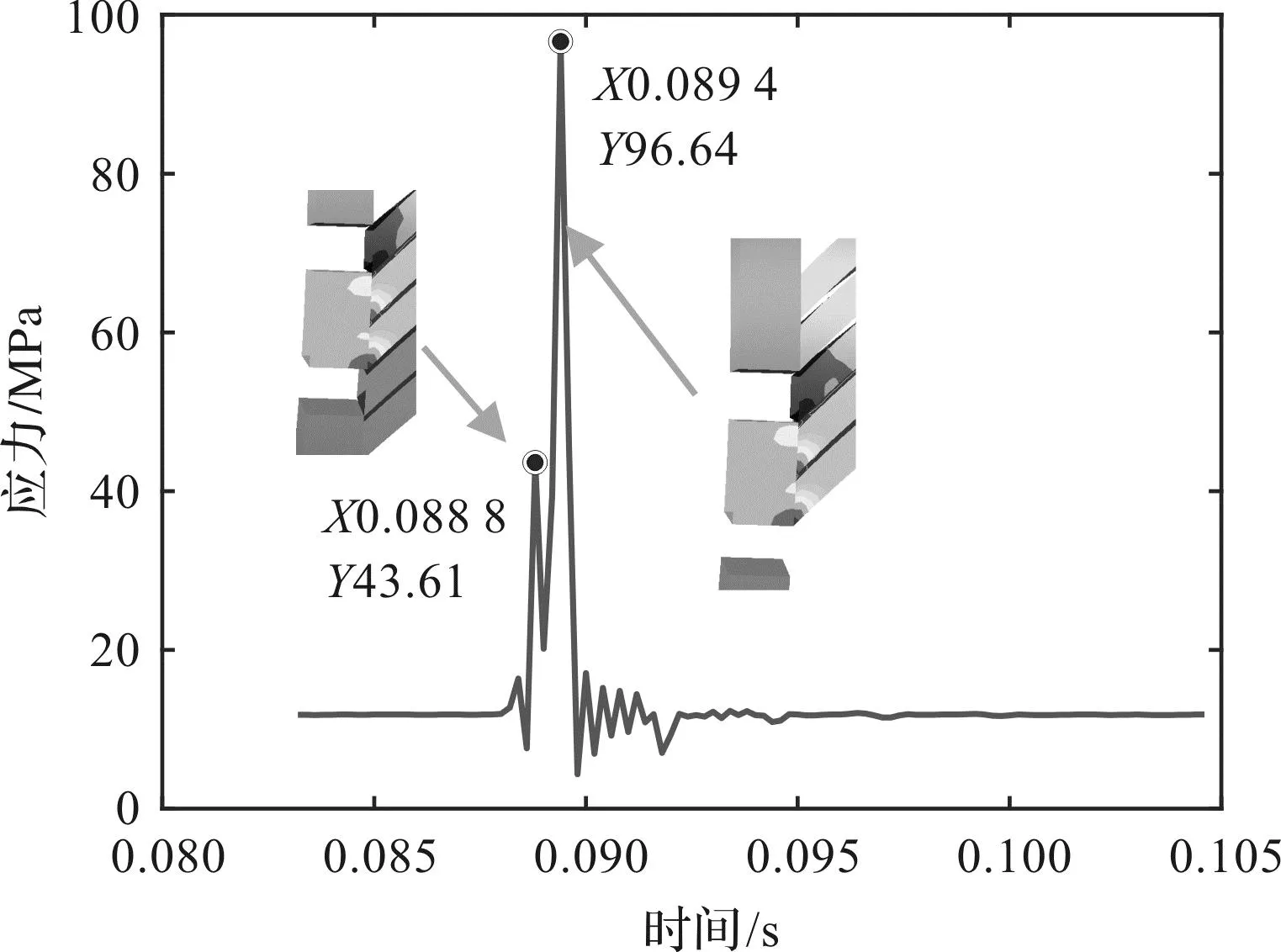
图12 迎风侧插片第1节点应力-时间曲线Fig.12 Stress-time curve of the first node of the windward side insert
由图8~图12可知:位移最大时刻与应力最大时刻相同;振荡管插片应力最大处为插片与内外筒连接处,最大应力值为97 MPa,低于不锈钢材料许用强度137 MPa;最大应力和次大应力发生时刻与大位移发生时刻规律相同。
3.3 模态分析
弯曲流道振荡管迎风侧插片位移和应力动态响应分析结果表明:在非定常流体激励载荷作用下,振荡管插片位移和应力值均在安全范围内。
为了判断气体波动能否引起振荡管振动问题,笔者对第1节点压力载荷和振荡管插片对应位置的位移分别进行傅里叶变换,得到弯曲流道压力和位移幅频特性曲线,如图13所示。
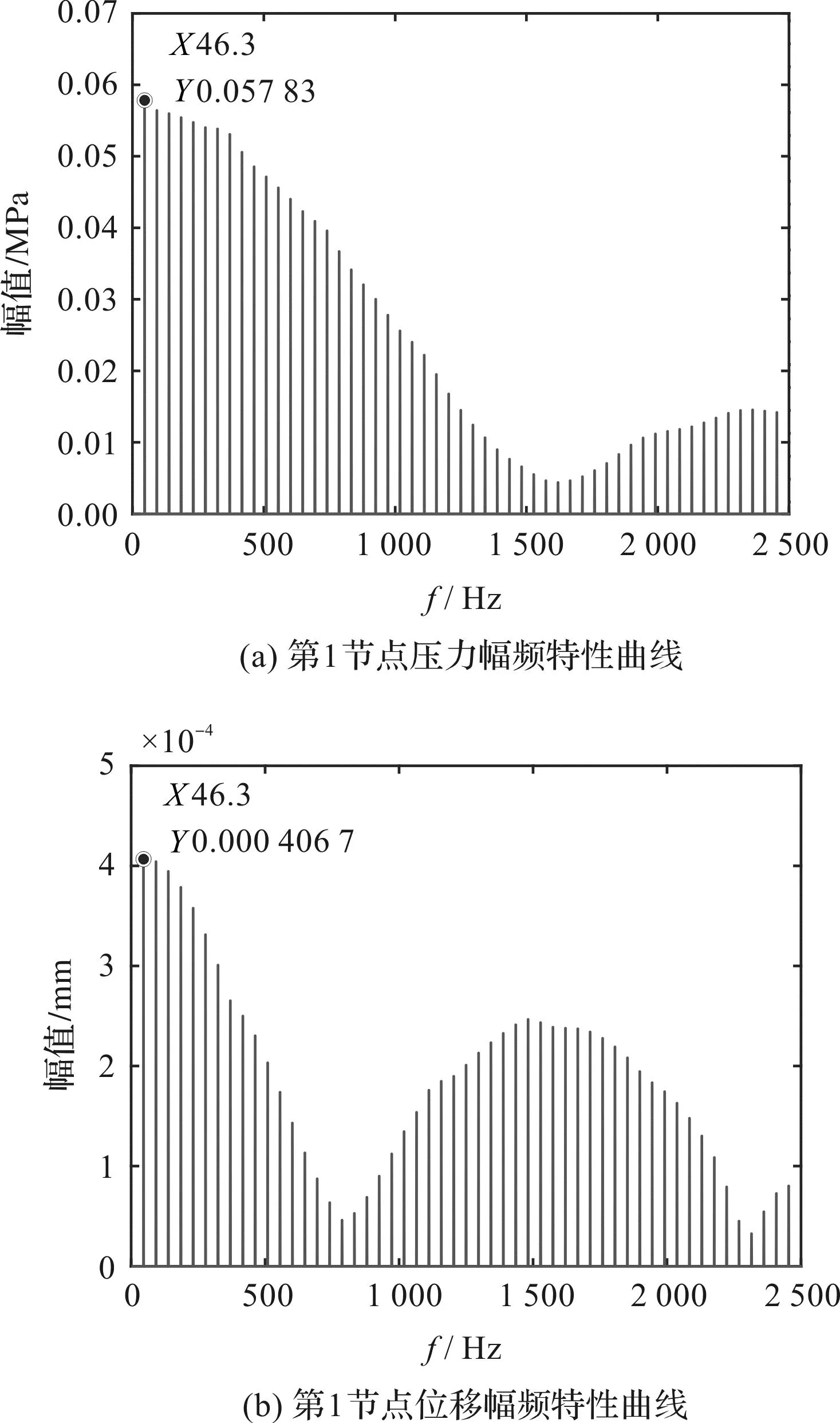
图13 弯曲流道压力和位移幅频特性曲线Fig.13 Pressure and displacement amplitude-frequency characteristic curves of curved channel
由图13可知:弯曲流道振荡管迎风侧第1节点压力最大节点的流体激励载荷和振荡管插片位移频率均为46.3 Hz,与该工况下气波机转动频率46.7 Hz基本一致,这表明振荡管插片的受迫振动是由气波机电机旋转引起的。
相同工况下,直流道气波机振荡管振动幅值最大节点为第7节点,其直流道位移时程和幅频特性曲线,如图14所示。
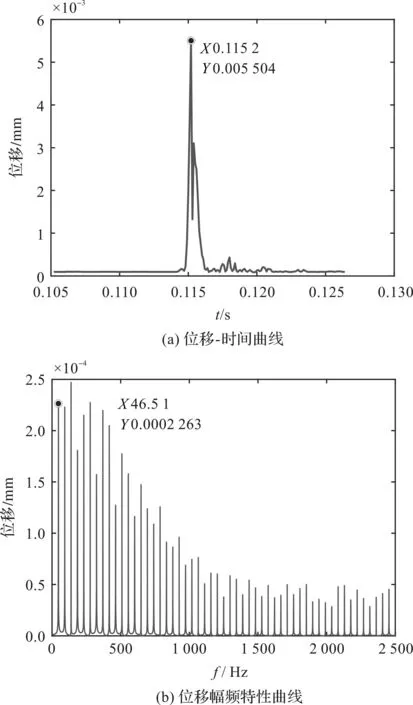
图14 直流道位移时程和幅频特性曲线Fig.14 Displacement time-history and amplitude-frequency characteristic curvesof straight channel
对比弯曲流道和直流道气波机[15]位移动态响应可知:在相同工况下,弯曲流道位移峰值是直流道的1.74倍,但是二者振动频率基本相同,均与转速频率46.7 Hz一致。
为了进一步明确气波机是否会发生共振,笔者对波转子进行模态分析,得到了波转子的前4阶模态,如表3所示。

表3 波转子前4阶模态
表3中,波转子的第1阶模态为87.76 Hz,与流体激励频率和电机旋转频率均不在共振区间内,因此可以判断气波机不会发生共振。
4 结束语
为研究弯曲流道气波机在非定常高频高压流体激励载荷作用下能否安全运行,笔者开发了弯曲流道气波机波转子三维流固耦合数值计算模型,并对气波机振荡管管内流场、结构动态响应及振动特性进行了研究。
研究结论如下:
1)弯曲流道振荡管内压力波动在0.069 4 MPa~1.141 0 MPa范围内,并且存在明显的压力间断,压力最大值集中在振荡管高压气体入口处,峰值高于入口压力的14.1%。在一个旋转周期内,振荡管同一点的迎风侧与背风侧压差在-0.185 6 MPa~0.971 2 MPa之间;
2)弯曲流道气波机振荡管内位移振幅最大值为0.009 6 mm,是直流道的1.74倍。虽然弯曲流道振荡管气波机插片位移振幅高于直流道振荡管气波机,但是其幅值仅在10-2mm以下,满足0.2 mm的工程设计要求,因此可以判断波转子不会与进出气口发生动静部件摩擦;
3)弯曲流道和直流道气波机振荡管内流激力及受迫振动频率均在46 Hz~47 Hz之间,与气波机电机转速频率相当,但远离气波机波转子固有频率,因此可以判断其不会发生共振。
笔者后续将重点关注振荡管进气角度、排气角度和插片厚度等对波转子动态响应特性的影响,以便为波转子的结构优化提供参考。
