IMRPE和AO-SVM在往复压缩机故障识别中的应用*
2023-12-20李占锋张军昌
李占锋,张军昌
(1.烟台职业学院 机械工程系,山东 烟台 264670;2.西北农林科技大学 机械与电子工程学院,陕西 杨凌 712100)
0 引 言
往复压缩机的工作环境恶劣且运行时间长,其运行过程中极易出现故障。因此,对压缩机的状态进行检测与诊断具有重要意义[1-3]。
近年来,熵值方法,如排列熵(permutation entropy,PE)被广泛用于故障诊断领域[4]。SHI Zong-li等人[5]采用PE方法表征滚动轴承的工况,有效反映了轴承的故障属性;但PE仅进行单尺度计算,分析不全面。为此,赵建岗等人[6]采用多尺度排列熵(multiscale permutation entropy,MPE)提取旋转机械的故障特征,诊断结果证明了MPE的有效性;但MPE采用的是传统粗粒化处理,随着尺度的增加,MPE出现波动,特征质量不稳定。为增强PE的性能,BANDT C等人[7]采用反向排列熵(reverse permutation entropy,RPE)分析人类脑电信号,准确度量了脑电信号的复杂度;但RPE只用于进行单尺度的分析,遗漏了其他尺度上的有效信息,特征提取得不够完整[8]。
在分类器方面,支持向量机被广泛应用于故障识别领域。然而,SVM的惩罚系数和核系数均会影响分类器的泛化性,一般要采用优化算法对其进行优化[9]。姜保军等人[10]采用遗传算法对SVM进行优化,采用优化后的SVM准确识别了齿轮箱的故障类型;但遗传算法的局部寻优能力较差,难以获得全局最优解。刁宁昆等人[11]采用粒子群算法优化支持向量机,采用优化后的SVM进行了滚动轴承的故障识别,有效识别了滚动轴承的故障类型;但粒子群算法的全局寻优能力较差。因此,迫切需要采用具有较为全面的全局和局部寻优能力的优化算法来搜索SVM的参数。
针对上述问题,笔者提出改进多尺度反向排列熵方法,以解决MPE的熵值波动和RPE单一尺度分析的问题。在此基础上,笔者提出基于IMRPE、t-SNE[12]和天鹰优化器优化支持向量机的往复压缩机故障诊断方法,利用往复压缩机数据集对IMRPE-t-SNE-AO-SVM方法进行实验,并且开展多个维度的对比。
1 算法原理
1.1 改进多尺度反向排列熵
1.1.1 多尺度反向排列熵算法
多尺度反向排列熵(multiscale reverse permutation entropy,MRPE)指标可以很好地表征非线性序列在多个尺度上的复杂特性和动力学响应。当滚动轴承出现故障后,振动信号的动力学特性也随之发生明显的变化,因此可以用MRPE提取故障特征。
对于振动信号X={x1,x2,…,xN},MRPE的理论如下:
1)对原始信号进行粗粒化处理,得到粗粒化序列Yτ={yτ(j)}如下:
(1)
式中:τ为尺度因子。
2)在不同尺度因子下,计算粗粒化序列Yτ的反向排列熵值,则MRPE定义如下:
EnMRPE(X,m,t,τ)=EnRPE(Yτ,m,t)
(2)
式中:m为嵌入维数;t为时间延迟;EnRPE为反向排列熵[13]。
1.1.2 改进多尺度反向排列熵算法
MRPE避免了RPE单尺度分析的缺陷,但MRPE在进行粗粒化处理时熵值偏差会随尺度的增加而逐渐增大。因此,笔者通过对某一尺度下的多个粗粒片段的RPE值进行平均,来缓解由于粗粒序列变短而造成RPE熵值突变的概率,尽可能确保熵值结果更加精确[14]。
对于X={x1,x2,…,xN},改进多尺度反向排列熵的计算过程如下:
(3)
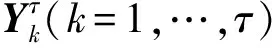
(4)
IMRPE与嵌入维数m、时间延迟t、尺度因子τ和数据长度N相关。m过小时,重构向量长度过短,算法无法准确检测信号的动态突变;相反,m取值过大,不仅加大数据量,而且无法准确表征信号的微弱波动,因此m的范围为[4,7],笔者设置为5。t对IMRPE的影响可以忽略,设置为1。尺度因子的设置没有确切的标准,通常设置为τ≥10,笔者设置为25。数据长度对算法的性能有较大的影响,需要进行合理的设置。
为说明IMRPE对N的敏感性,笔者分别采用不同信号长度的白高斯噪声(Gaussian white noise,WGN)和1/f噪声设置下面的仿真实验,分别采用IMRPE和MRPE计算10组WGN和1/f噪声在不同长度下的熵值,以及不同长度下两者的标准差差值。
结果如图1所示。
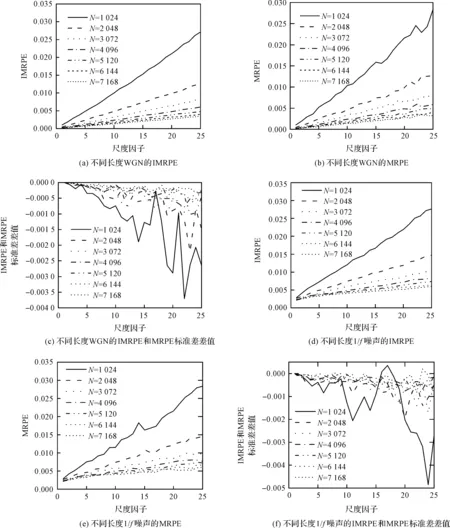
图1 不同数据长度仿真信号的IMRPE和MRPE均值与标准差差值Fig.1 IMRPE and MRPE mean and standard deviation difference of simulated signals with different data lengths
从图1发现:WGN和1/f噪声的熵值曲线随着尺度的增加而逐渐增加,证明了仿真信号的复杂度在全频段上呈现增加的趋势。而WGN和1/f噪声的IMRPE曲线呈直线上升趋势,而MRPE曲线存在波动,这证明了在各个尺度上IMRPE的熵值都具有较好的稳定性;反之,MRPE由于其粗粒化处理的局限性而存在波动。其次,两个仿真信号的标准差差值都小于0,即IMRPE的标准差小于MRPE,这证明IMRPE的稳定性高于MRPE,证明了IMRPE方法的优越性。此外,可以发现,数据长度为N=1 024、2 048和3 072时,熵值曲线未与其他曲线重合。而当N=4 096时,熵值非常稳定,且标准差也非常小,因此笔者选择N=4 096进行分析。
1.2 天鹰算法优化支持向量机
1.2.1 天鹰优化算法
天鹰优化算法是最近刚提出的一种启发式优化算法,其具有较强的全局寻优性能,能够以较快的速度收敛得到稳定的最优解[15-16]。
天鹰算法的优化流程如下:
1)垂直俯冲。当天鹰发现目标区域后,会通过盘旋在全局初步挑选最优捕猎范围,以判定最佳解的所在探索空间,表示如下:
(5)
式中:X1(t+1)为t+1代的解;Xbest(t)为最优解,指代目标猎物的最近坐标;t,T为目前迭代和最大迭代次数;XM(t)为第t次迭代时当前解的坐标均值;δ为[0,1]范围内的随机量;dim为问题的维数;
2)短滑翔攻击。当从高处翱翔锁定猎物范围时,天鹰会在目标上方盘旋,以减小捕猎的范围,即最小化解的搜索空间,表示如下:
(6)
式中:XR(t)为[1,N]范围内的随机数;d为维数空间;L(d)为狩猎飞行分布函数;
3)低空飞行。当精确定位目标区域,且天鹰准确着陆和攻击时,天鹰在定好的目标区域利用低飞慢降的出击方式来查看目标的回应,缓慢地靠近目标,表示如下:
X3(t+1)=(Xbest(t)-XM(t))α-δ+((ub-lb)δ+lb)λ
(7)
式中:α,λ为调整参数,笔者设置为0.1;ub,lb为代表求解问题的上界和下界;
4)行走抓捕。当天鹰靠近目标时,根据目标的运动在大地上空来狩猎目标,进行快速地收敛,表示如下:
(8)
式中:QF为平衡探索策略的质量函数;G1为在捕捉猎物中天鹰的各种运动;G2为天鹰在狩猎过程中的飞行斜率;X(t)为第t次迭代的解。
1.2.2 天鹰算法优化支持向量机流程
支持向量机的惩罚系数和核函数会影响其分类性能,人为设置难以获得最佳的参数组合,为此笔者采用天鹰算法对SVM进行优化,当满足终止迭代条件时,AO算法会输出最佳的参数。
AO-SVM算法的流程如下:
1)对AO和SVM的各个参数进行初始化,设置AO算法的种群数量、最大迭代次数、待求解问题的上限ub和下限lb;
2)输入待分类的特征样本,进行归一化处理,并分为训练集和测试集;
3)通过交叉验证,对训练集进行训练,将交叉验证的准确率作为天鹰个体的适应度函数,得到最佳适应度和坐标;
4)计算天鹰新个体的适应度值,且与获得的最佳个体进行适应度对比;
5)评估迭代次数是否达到最大迭代次数,若是,则得到最佳参数组合,进而得到最佳SVM分类器,结束诊断过程;若否,则重复AO算法中天鹰垂直俯冲和攻击等行为,直至输出最佳解,得到最优AO-SVM分类模型。
2 基于IMRPE-t-SNE-AO&SVM的故障诊断方法
2.1 故障诊断流程
针对往复压缩机的故障特征提取和模式识别问题,笔者采用IMRPE提取故障特征,构造故障特征向量;随后,利用t-SNE对初始故障特征进行降维,构建低维特征向量;最后,利用AO-SVM作为故障分类模型进行识别,判断压缩机的故障类型。
该诊断模型的具体步骤如下:
1)在某一频率下采用麦克风设备采集往复压缩机不同状态的声音信号;
2)利用IMRPE提取声音信号样本的故障信息,构建故障特征向量,并将其划分为训练和测试样本;
3)利用t-SNE对特征样本进行降维,构造低维敏感特征样本;
4)利用AO对SVM的惩罚系数和核函数进行优化,构建AO-SVM多故障分类器,通过训练样本进行训练,得到完备的分类器;
5)将测试样本输入至训练好的分类器,进行压缩机故障类型的识别。
基于IMRPE-t-SNE-AO-SVM的故障诊断方法的流程如图2所示。
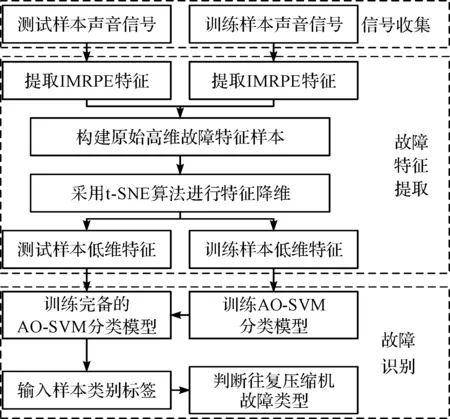
图2 IMRPE-t-SNE-AO-SVM故障诊断方法的流程图Fig.2 A flowchart of the IMRPE-t-SNE-AO-SVM fault diagnosis method
2.2 故障诊断实验
为了验证基于IMRPE-t-SNE-AO-SVM的故障诊断方法的有效性,笔者利用印度理工学院提供的往复压缩机声信号数据进行实验[17-18]。
实验平台如图3所示。
麦克风设备放置在距离压缩机约1.5 cm处的位置,通过麦克风以50 kHz的频率采集往复压缩机的声音信号,总的采集时间为5 s。对往复压缩机在健康(标记为1)、进气阀故障(标记为2)、出口阀故障(标记为3)、止回阀故障(标记为4)和活塞环故障(标记为5)下的声音信号进行了收集。每种工况分为45组样本,每个样本的长度为4 096,其中25组样本作为训练集,剩余20组样本作为测试集。
笔者利用IMRPE方法提取往复压缩机声信号的故障特征,为了验证IMRPE方法的有效性,将其与MRPE和MPE进行对比。
结果如图4所示。
从图4中可以发现:故障特征曲线的区分度不太明显,直接利用原始故障特征进行故障识别难以获得最佳的识别结果。但IMRPE特征的标准差小于MRPE方法,

图3 往复压缩机实验平台Fig.3 Reciprocating compressor test platform
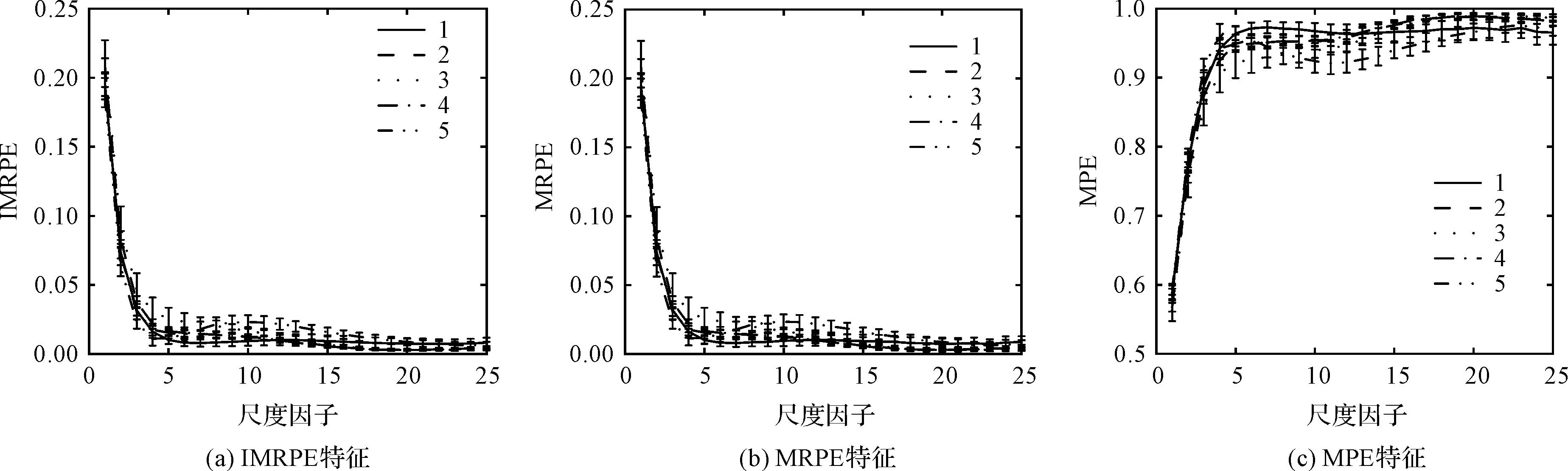
图4 IMRPE、MRPE和MPE故障特征曲线Fig.4 Fault characteristic curves of IMRPE, MRPE and MPE
这证明了改进粗粒化处理的有效性。为了预先降低故障特征的维数,笔者选择IMRPE前10个特征进行后续分析。
随后,为了进一步地提高故障特征的区分度,增强组合特征的质量,笔者利用t-SNE对前10个特征进行降维和优化,将故障特征降维至二维。
结果如图5所示。

图5 IMRPE、MRPE和MPE的降维可视化Fig.5 Dimension reduction visualization of IMRPE, MRPE and MPE
从图5可以发现:IMRPE在降维后取得了最佳的效果,5种状态的特征样本都各自得到了较好的区分,样本1、样本5和样本4有比较明显的聚类中心,这证明IMRPE特征在经过t-SNE降维后能够很好地分辨往复压缩机故障。但样本2和样本3存在部分样本混叠,这证明这两类样本不易进行区分。而MPE能够较好地区分样本1和样本5,但是聚集程度较IMRPE差,而MRPE的聚类效果较差,样本1和样本5与其他3种样本发生了部分的混叠。因此,IMRPE的降维效果优于MRPE和MPE,证明了IMRPE方法的特征提取性能优于MRPE和MPE。
最后,笔者利用AO算法对SVM的惩罚系数和核函数进行优化。同时,为了证明AO算法在优化中的有效性和优越性,笔者将其与粒子群算法(particle swarm optimization,PSO)、鲸鱼算法(whale optimization algorithm,WOA)和灰狼算法(grey wolf optimizer,GWO)进行比较[19-20],每种算法的迭代次数设置为50,种群规模设置为20。
迭代过程中的适应度曲线如图6所示。
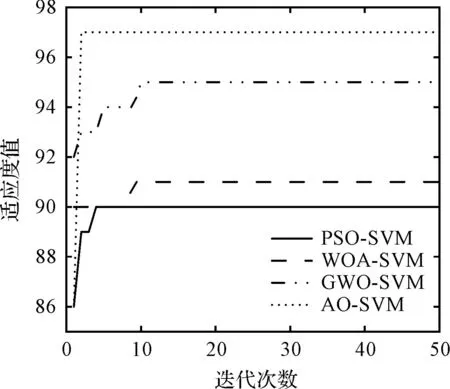
图6 4种优化算法的迭代曲线Fig.6 The iterative curve of four optimization algorithms
从图6可以发现:AO算法仅需1次迭代即获得了最优解,这证明AO具有较高的优化效率。同时AO算法生成的最优解也是最好的,优于另外3种算法,证明AO的全局优化性能较优,而WOA和PSO算法虽然也较快地得到了最优解,但其最优解仅是局部最优解。因此,基于AO的支持向量机具有最高的优化效率和优化性能。经过AO优化后的惩罚系数和核函数值为10.05和0.77。
笔者将IMRPE提取的故障特征输入至AO-SVM中进行故障识别。
结果如图7所示。
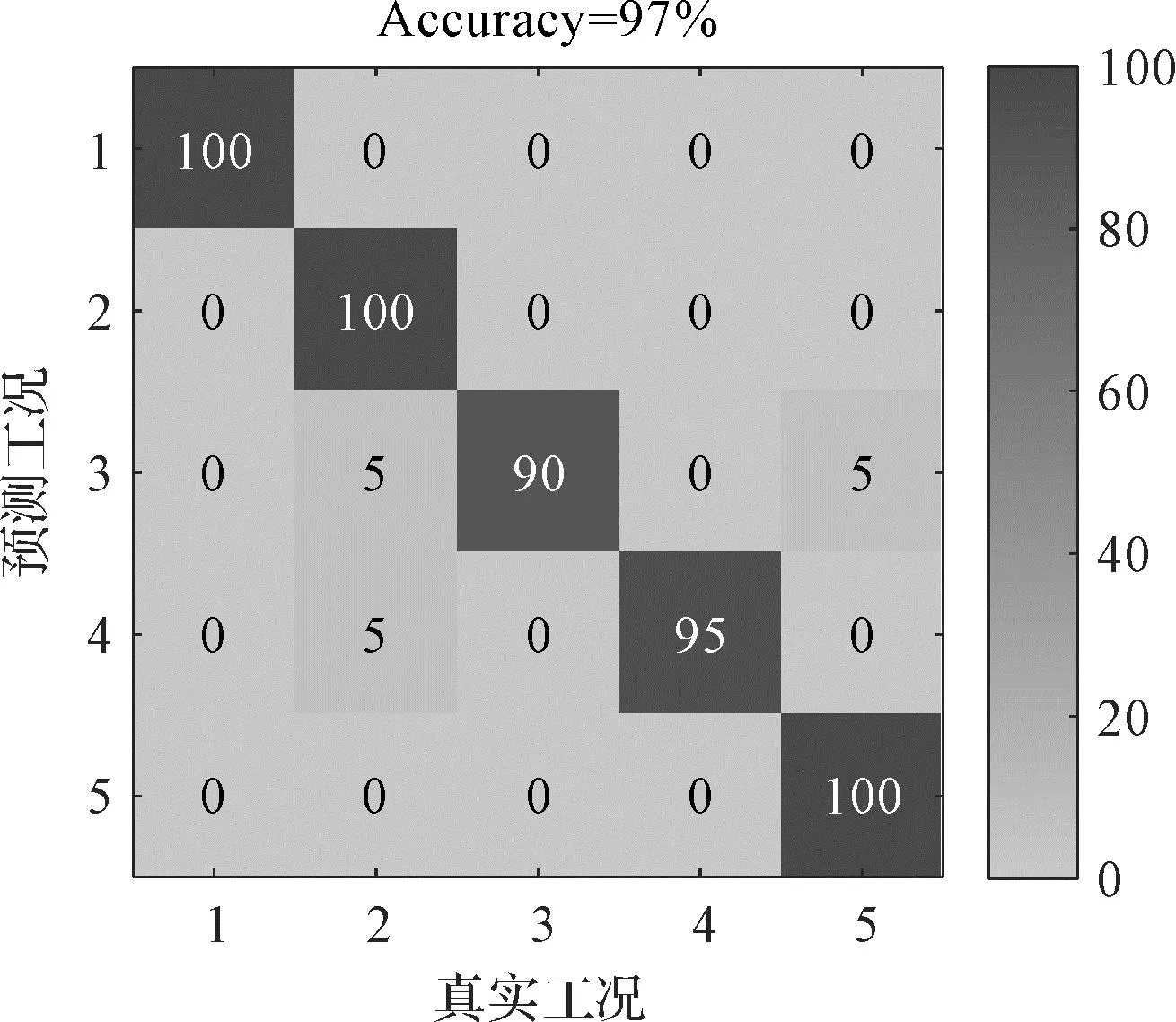
图7 IMRPE-t-SNE-AO-SVM的故障识别结果Fig.7 Fault identification result of IMRPE-t-SNE-AO-SVM
从图7可以发现:基于IMRPE-t-SNE-AO-SVM的故障诊断方法取得了97%的识别准确率,有1个样本3被错误归类为样本2,1个样本3被错误归类为样本5以及1个样本4被错误归类为2,这与之前的可视化结果一致,即样本3和样本5和样本4互相混叠,这证明了IMRPE-t-SNE-AO-SVM方法在往复压缩机故障识别的有效性。
随后,为了验证IMRPE方法的有效性,笔者将MRPE和MPE提取的故障特征输入至AO-SVM中进行故障识别。3种方法的详细故障诊断结果和特征处理时间如表1所示。
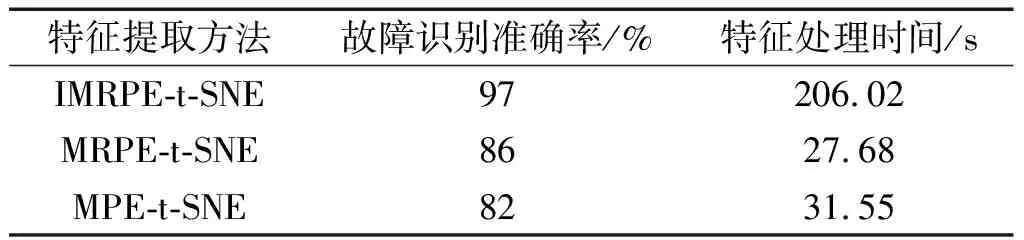
表1 3种方法的详细故障诊断结果
从表1可以发现:IMRPE-t-SNE-AO-SVM方法的特征处理时间较多,但考虑到有5种工况,因此特征提取时间相对可以接受。
随后,为了验证进行t-SNE降维的有效性和必要性,笔者将由IMRPE、MRPE和MPE提取的故障特征直接输入至AO-SVM进行故障识别。
结果如表2所示。
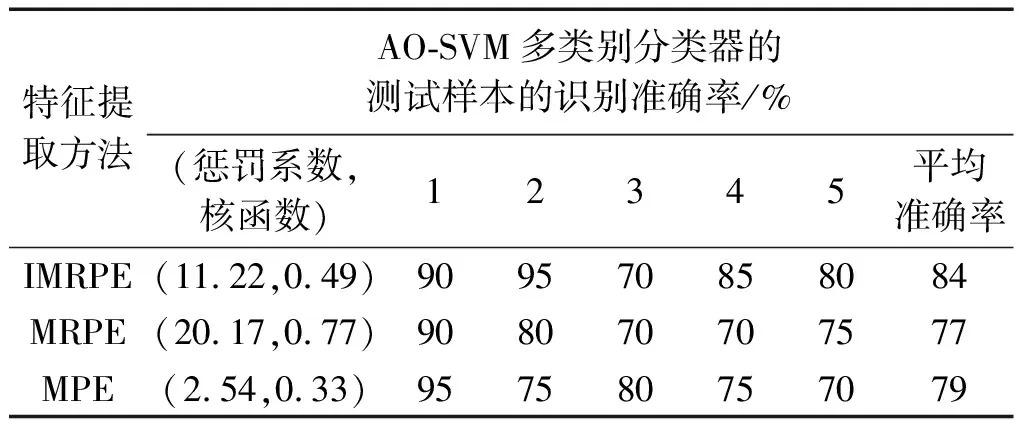
表2 不同方法的测试集识别结果
从表2可以发现:特征没有经过降维直接进行分类的准确率低于表1,这证明了利用t-SNE进行降维的有效性。这主要是因为原始故障特征存在过多的冗余信息,在分类识别时会互相干扰,影响了识别的结果。
实际情况下,声音信号在采集时存在较多的背景噪声,有必要验证IMRPE-t-SNE-AO-SVM方法的抗噪性能。为此,笔者在进行特征提取时引入了不同信噪比的噪声,分别是0 dB、5 dB、10 dB、15 dB和20 dB,完成不同信噪比下的故障特征提取后,将其输入至AO-SVM中进行故障识别[21]。
结果如表3所示。
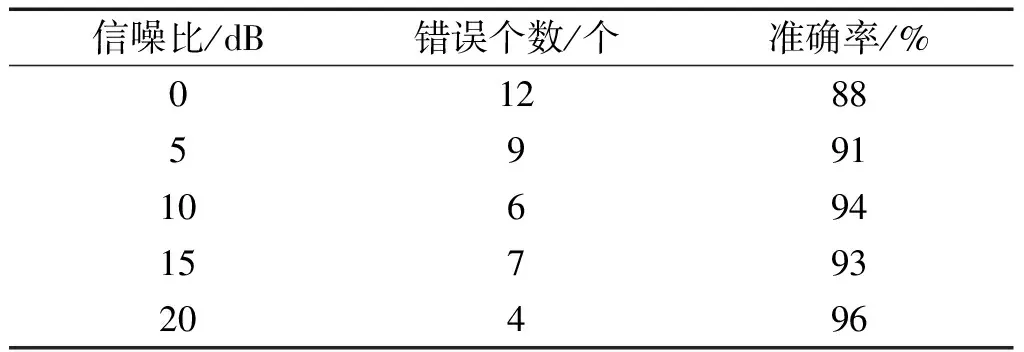
表3 不同信噪比下IMRPE-t-SNE-AO-SVM方法的诊断结果
从表3可以发现:即使信噪比较低,IMRPE-t-SNE-AO-SVM方法的准确率也达到了88%以上,而当信噪比为20 dB时,准确率达到了96%,证明IMRPE-t-SNE-AO-SVM方法具有良好的抗噪性,受噪声的影响较小。
最后,为了验证AO-SVM在故障识别中的有效性,笔者将其与之前的PSO-SVM、WOA-SVM以及GWO-SVM分类器进行对比。笔者将IMRPE+t-SNE等方法提取的故障特征分别输入至4种分类器进行故障识别。
4种多类别分类器对3种特征提取方法的测试样本识别结果如图8所示。
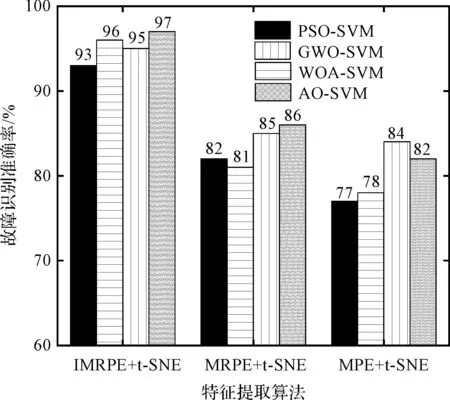
图8 4种分类器对3种特征提取方法的测试样本识别准确率Fig.8 Identification accuracy of four classifiers on test samples of three feature extraction methods
从图8可以发现:采用AO-SVM分类器识别IMRPE+t-SNE特征时,其取得了最高的识别准确率,这证明了AO-SVM方法的有效性。而与PSO-SVM、WOA-SVM和GWO-SVM分类器相比,AO-SVM对IMRPE和MPE特征的识别结果最好,验证了其优越性。
总之,AO-SVM在往复压缩机的故障识别中具有较好的表现。
3 结束语
针对往复压缩机的故障识别问题,笔者提出了一种基于IMRPE、t-SNE和AO-SVM的往复压缩机声信号故障诊断方法,利用往复压缩机声信号数据进行了实验分析,并开展了对比研究。
研究结论如下:
1)噪声信号和声音信号的实验表明,IMRPE方法缓解了MRPE粗粒化处理的缺陷,熵值更加可靠和稳定;
2)故障诊断结果表明,AO-SVM仅需1次迭代即可以获得97%的准确率,迭代速度和性能都优于PSO-SVM、WOA-SVM和GWO-SVM模型;
3)基于IMRPE+t-SNE和AO-SVM的故障诊断模型能用于准确地判断故障类型,准确率达到了97%,当信噪比为20 dB时,准确率也能够达到96%,证明该方法即使受到噪声的影响,依然能获得可靠的故障识别结果。
基于IMRPE+t-SNE和AO-SVM的故障诊断方法受噪声的影响不可忽略,后续笔者将结合去噪方法对信号进行预处理,以减小噪声对该诊断方法的干扰。
