基于HRFDE和GSA-PNN的旋转机械故障识别模型*

赫大雨,王 强

(1.吉林铁道职业技术学院 铁道机车学院,吉林 吉林 132299;2.东南大学 机械工程学院,江苏 南京 210096)

0 引 言

旋转机械是较为常见的机械设备,研究针对旋转机械的故障诊断方法对确保设备平稳安全地运行具有重要意义[1-2]。

旋转机械在发生故障后,振动信号中将出现之前不存在的冲击成分和谐波分量,使得信号的复杂性发生突变。因此,通过对旋转机械的振动信号进行分析,以此来检测设备的故障是一种行之有效的方法[3]。但是由于该振动信号呈现出复杂的非线性和非平稳性,因此,在针对旋转机械的故障诊断中,非线性动力学分析方法的应用非常广泛。非线性动力学分析方法以样本熵[4]、排列熵[5]、模糊熵[6]、散布熵[7]和多尺度散布熵(multiscale dispersion entropy,MDE)[8]为代表。

MDE具有计算效率高、特征提取能力强等优点。乔新勇等人[9]将MDE用于柴油机的故障诊断,结果表明,MDE在故障诊断中具有有效性;然而MDE的粗粒化处理只考虑了时间序列的低频特征,而忽略了高频特征中的故障信息。随后,柯赟等人[10]基于层次熵和散布熵,提出了层次散布熵(HDE),借此全面地提取到了信号中的故障特征,并对喷油器故障进行了精准识别;然而HDE只考虑了信号幅值的绝对性而忽略了相对性,无法有效地评估信号的波动性。随后,KE Yun等人[11]充分考虑了信号的波动性,提出了层次波动散布熵(hierarchical fluctuation dispersion entropy,HFDE),并将其用于喷油器的故障诊断,有效地提取了其故障特征;然而HFDE无法提取信号的深层次信息,其特征提取的效果还有待提升。

为了进一步提高HFDE的特征提取性能,JIAO Shang-bin等人[12]提出了反向波动散布熵(reverse fluctuation dispersion entropy,RFDE),该方法在故障特征提取过程中,同时考虑了波动散布熵的幅值、波动信息和反向排列熵的距离信息,而基于该方法的齿轮故障信号识别结果也证明了RFDE的有效性;然而RFDE无法进行信号的多尺度分析。为此,宋来建等人[13]127-128和周经龙等人[14]分别提出了时移多尺度反向波动散布熵和精细复合多尺度反向波动散布熵,并将它们分别应用于旋转机械和滚动轴承的故障诊断,结果也验证了反向波动散布熵的有效性;然而,上述2种方法虽然实现了信号的深层次特征提取目的,但由于所采用的粗粒化处理方法的固有缺陷,其无法提取信号高频特征中的故障信息。

在模式识别方面,由于具有较快的收敛速度以及较强的处理非线性数据的能力,概率神经网络(PNN)被广泛应用于故障的诊断领域。但是其性能易受到平滑因子设置的影响,造成故障分类结果的不稳定。为此,刘福政等人[15]采用粒子群算法(particle swarm optimization,PSO)对PNN的平滑因子进行了搜索,建立了参数最优的PNN分类模型,并将其用于滚动轴承的故障识别,结果验证了该分类器的有效性;但是PSO易陷入局部最优。党建等人[16]采用萤火虫算法对PNN进行了优化,对回转窑的故障进行了有效识别;但萤火虫算法的全局优化性能依然不足。因此,迫切需要采用具有良好全局优化性能和局部优化性能的算法对PNN进行优化,以构建网络参数最优的PNN分类模型。

针对上述问题,为了从振动信号中提取出更高质量的故障特征,以及准确判断旋转机械的故障类型,笔者提出层次反向波动散布熵(HRFDE)方法,并将其用于提取旋转机械的故障特征,实现深层次故障特征的提取目的。

基于此,笔者将HRFDE用于提取旋转机械的故障特征,并采用引力搜索算法(GSA)优化PNN,在此基础上提出一种基于HRFDE和GSA-PNN的旋转机械故障诊断方法。

首先,利用HRFDE提取旋转机械的故障特征,以准确表征旋转机械的不同故障状态;随后,采用引力搜索算法对概率神经网络进行优化,构建网络参数最优的分类器,并进行训练;最后,利用训练好的分类器对故障样本进行识别,并基于滚动轴承和齿轮箱两组故障数据进行实验分析。

1 层次反向波动散布熵

1.1 多尺度反向波动散布熵

宋来建等人[13]126-127基于多尺度分析和反向波动散布熵的概念,提出了多尺度反向波动散布熵(MRFDE),并将其用于旋转机械的故障特征提取。

MRFDE的理论原理如下:

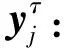
(1)

式中:τ为尺度因子,τ=1,2,…,n。

2)计算每个粗粒向量的RFDE,得到n个粗粒向量的RFDE值,将其表示为尺度因子τ的函数,称为MRFDE分析,其表达式如下:

(2)

综上可以发现,MRFDE将原始信号分割为多个子序列,进而从多个尺度测量信号的复杂度。然而,MRFDE所采用的粗粒化处理是对数据取平均的过程,其只提取了信号的低频成分,遗漏了高频成分。

1.2 层次反向波动散布熵

为了实现信号的高频分量分析目的,笔者基于层次分割对信号进行处理,提出了层次反向波动散布熵(HRFDE)。相较于MRFDE,HRFDE既能够实现信号的多尺度分析目标,也能够有效提取信号的低频和高频分量。

HRFDE的计算过程如下:

1)对于长度N的信号{u(i),i=1,2,…,N},给定平均算子Q0和差分算子Q1为:

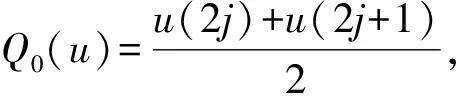
(3)

其中:N=2n;算子Q0和算子Q1的长度为2n-1。

根据算子Q0和Q1,原信号可以重构为:

u={(Q0(u)j+Q1(u)j),(Q0(u)j-Q1(u)j)}

(4)

当j=0或j=1时,矩阵Qj定义如下:

Qj(u)=

(5)

2)构造n维向量[γ1,γ2,…,γn]∈{0,1},则整数e可以定义为:

(6)

式中:e为对应向量[γ1,γ2,…,γn];

3)基于向量[γ1,γ2,…,γn],定义信号u(i)每一层分解的节点分量为:

uk,e=Qγn·Qγn-1·…·Qγ1(u)

(7)

式中:k为层次分析中的第k层。

原始信号u(i)在第k+1层的低频分量和高频分量分别由uk,0和uk,1表示。

信号u(i)的层次分解示意图如图1所示。

图1 信号u(i)的层次分解示意图(k=3)Fig.1 Schematic diagram of hierarchical decomposition of signal u(i)(k=3)

4)对每个层次分量进行RFDE分析,得到2k个层次分量的RFDE值,完成了信号的HRFDE计算任务(过程),其表达式为:

HRFDE=RFDE(uk,e,m,c,d)

(8)

综合上述分析,与MRFDE的粗粒化处理不同,HRFDE的层次分析将信号拆分为算子Q0和算子Q1,分别从低频和高频来表征信号的固有特性,使信号的复杂性分析更加全面和准确。

对于实际工程中的旋转机械而言,振动信号的高频部分也包含大量的故障信息,只利用信号的低频无法完全表征故障特性,充分利用信号中的高频信息很有必要。

1.3 参数设置和仿真分析

根据HRFDE的计算过程可知,对结果存在影响的参数包括:信号长度N、嵌入维数m、类别数c和时间延迟d。现分述如下:

1)m的设置会影响信号重构时重构向量的信息量,m过小会导致重构时丢失部分信息;反之m过大,会严重降低计算效率;

2)c的选择会影响模式的归类,c过小会导致幅值差距较大的散布模式被归为一类;反之c过大,会导致算法的抗噪性较差;

3)时间延迟d对算法的性能几乎没有影响。

宋来建等人[13]126对参数进行了研究。根据其建议,笔者将参数设置为m=2、c=5、d=1。

为了获得合理的数据长度,笔者对不同长度下的白噪声进行了研究。

不同长度白噪声信号的HRFDE结果,如图2所示。

图2 不同长度白噪声信号的HRFDEFig.2 HRFDE of white noise signals of different lengths

由图2可知:不同长度白噪声信号的HRFDE曲线均存在波动,但随着长度的增加,波动的趋势逐渐减弱,表明数据长度的增加有助于提高熵值的稳定性;此外,随着数据长度的增加,信号标准差也逐渐减小,但计算效率也随之降低。

因此,综合考虑算法的性能和效率,笔者将长度设置为N=2 048。

随后,为了对比HRFDE和MRFDE的性能,笔者构造了20个长度为2 048的白噪声信号,并分别利用HRFDE和MRFDE提取其反向波动散布熵值,同时计算了每个尺度的标准差,以评估算法的稳定性。

白噪声信号的HRFDE和MRFDE结果如图3所示。

图3 白噪声信号的HRFDE和MRFDEFig.3 HRFDE and MRFDE of white noise signal

由图3可知:对于白噪声信号而言,通过HRFDE计算得到的熵值随着层次节点而平稳变化,熵值变化与节点的变化相互独立,这与不同频带上白噪声的熵值近似不变的结论一致。而MRFDE计算的白噪声熵值会随着尺度的增加而逐渐变大,这与白噪声在各个频带具有一致复杂度的结论不符。这是由于MRFDE只提取了模拟信号的低频信息,遗漏了对应的高频信息,而HRFDE能够同时提取信号的低频和高频信息,从而获得更多有效和全面的信息。

此外,观察HRFDE和MRFDE的熵值误差棒可以发现,HRFDE曲线的误差棒明显小于MRFDE的误差棒,证明HRFDE的稳定性优于MRFDE。

2 GSA-PNN分类器

2.1 概率神经网络

概率神经网络(PNN)是在径向基神经网络的基础上,结合了密度函数估计和贝叶斯决策理论而得到的一种神经网络,其在样本分类领域得到了广泛的应用。滚动轴承样本为非线性和非平稳的信号,可充分利用PNN在处理非线性样本时具有高精度的优势[17]。

概率神经网络由输入层、模式层、求和层和决策层组成,其网络的结构如图4所示。

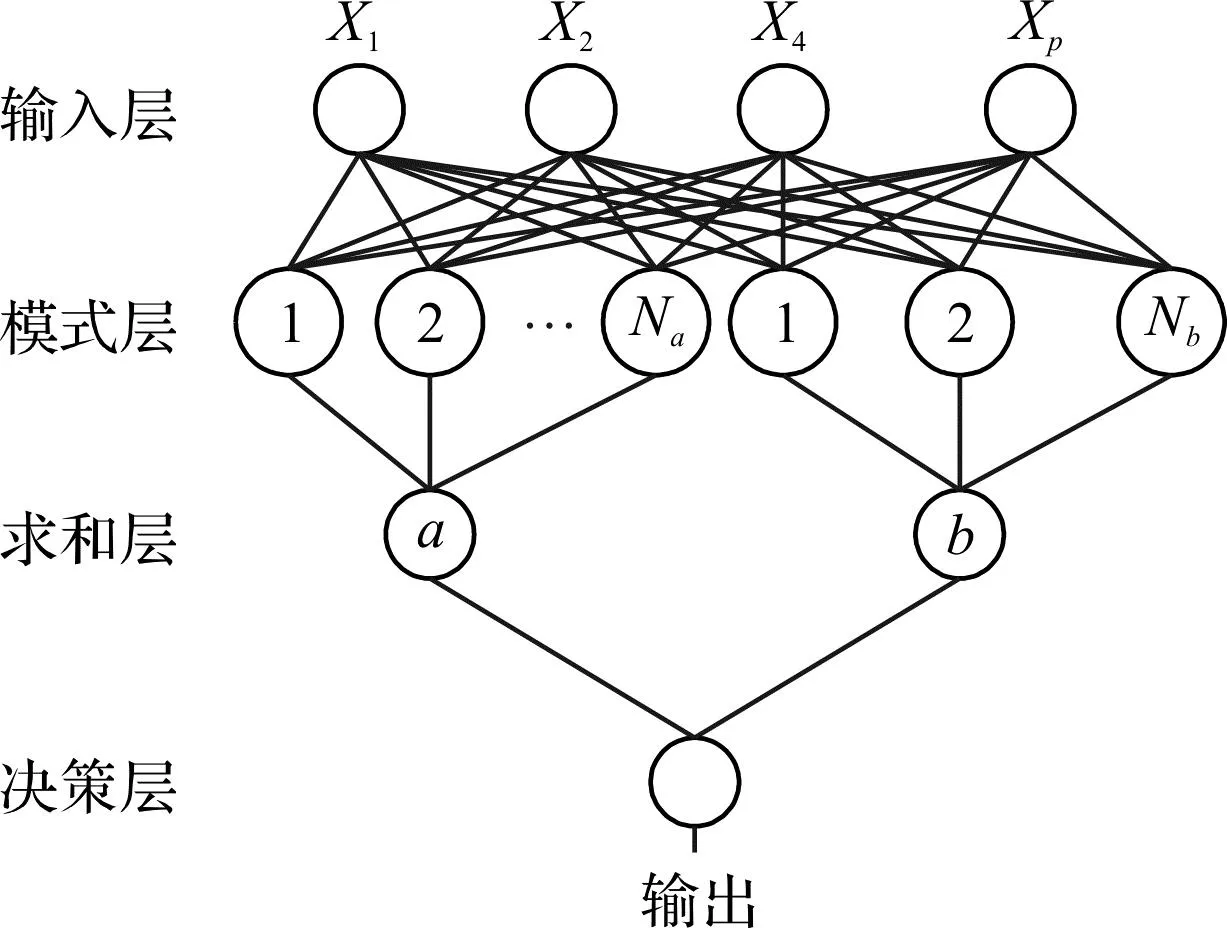
图4 概率神经网络的结构Fig.4 The structure of probabilistic neural networks

X为输入样本,X=(X1,X2,…,Xp);Na,Nb为输入向量与中心的距离;a和b分别为不同的信息类型。

2.2 引力搜索算法

接下来,笔者采用引力搜索算法(GSA)对PNN进行优化。

GSA算法是ESMAT R等人[18]通过借鉴牛顿万有引力的概念提出的一种新型的智能优化算法,其利用种群中各物体之间万有引力的相互作用,以此来实现优化信息共享的目的。郑近德等人[19]的研究已经证明了GSA用于优化的有效性。

GSA的具体原理如下:

假定有一个n维优化空间,种群X={x1,x2,…,xn}其包含N个粒子,定义第i(i=1,2,…,N)个粒子的坐标为:

(9)

首先,对粒子的坐标进行初始化。在时刻t,第i个粒子和第j个粒子之间的引力值定义如下:

(10)

式中:Mpi(t)为受力粒子i的惯性质量;Maj(t)为施力粒子j的惯性质量;ε为无物理意义的常数;G(t)为随t变化的引力常量;Rij(t)为粒子i和j之间的欧式距离。

其次,适应度值的大小关乎粒子的惯性质量Mi(t),适应度值越大,表示其越靠近最优解。基于下式进行粒子惯性质量的更新:

(11)

(12)

式中:fiti(t)为粒子i在t时刻的适应度值;best(t)为所有粒子中最好的适应度值;worst(t)为所有粒子中最差的适应度值。

在每一次的迭代中,粒子的速度和坐标都会根据牛顿第二定律进行更新,其公式如下:

(13)

(14)

(15)

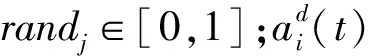
实验中,笔者设置GSA的种群数量为30,迭代次数为100,PNN的平滑因子初始值设置为0.1,优化范围设置为[0,1]。

GSA优化PNN的详细流程,即GSA-PNN优化流程图如图5所示。

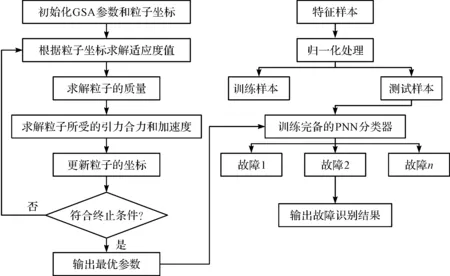
图5 GSA-PNN优化流程图Fig.5 Optimization flow chart of GSA-PNN

3 基于HRFDE和GSA-PNN的诊断方法

鉴于HRFDE方法在进行特征提取中的有效性和优越性,笔者提出了一种基于HRFDE和GSA-PNN的旋转机械故障诊断方法。

该诊断方法的具体流程如下:

1)采集n种不同工况的旋转机械振动信号,将其分割为等长的h个样本,对全部样本进行HRFDE计算,选择前8个HRFDE值作为特征向量;

2)在不同工况样本的特征向量中,随机抽取i个样本组成训练样本,剩余样本组成测试样本;

3)利用训练样本的特征向量对基于GSA-PNN的多故障分类器进行训练,生成完备的训练模型;

4)将测试样本输入至训练完备的模型,根据模型的输出来判断旋转机械的故障类型和严重程度。

4 故障诊断实验与分析

4.1 轴承故障诊断实验

4.1.1 故障数据来源

滚动轴承的实验数据由美国凯斯西储大学的轴承数据库提供(该数据库中的轴承型号为6205-2RS JEM SKF深沟球轴承)。

轴承实验装置如图6所示。

图6 轴承实验平台Fig.6 Bearing test platform

此处电机的负载设置为0 hp,转速为1 797 r/min。基于不同的故障尺寸,笔者以12 kHz的频率收集了驱动端滚动轴承在4种状态下的10种工况的振动信号,其中故障尺寸分别为0.177 8 mm、0.355 6 mm、0.533 4 mm,故障的深度为0.279 4 mm。

对于每种工况均收集40组样本,数据长度为2 048,同时为模拟实际条件下缺乏训练样本的情况,笔者随机抽取10组样本用于训练,剩余30组用于测试。

样本的详细信息如表1所示。

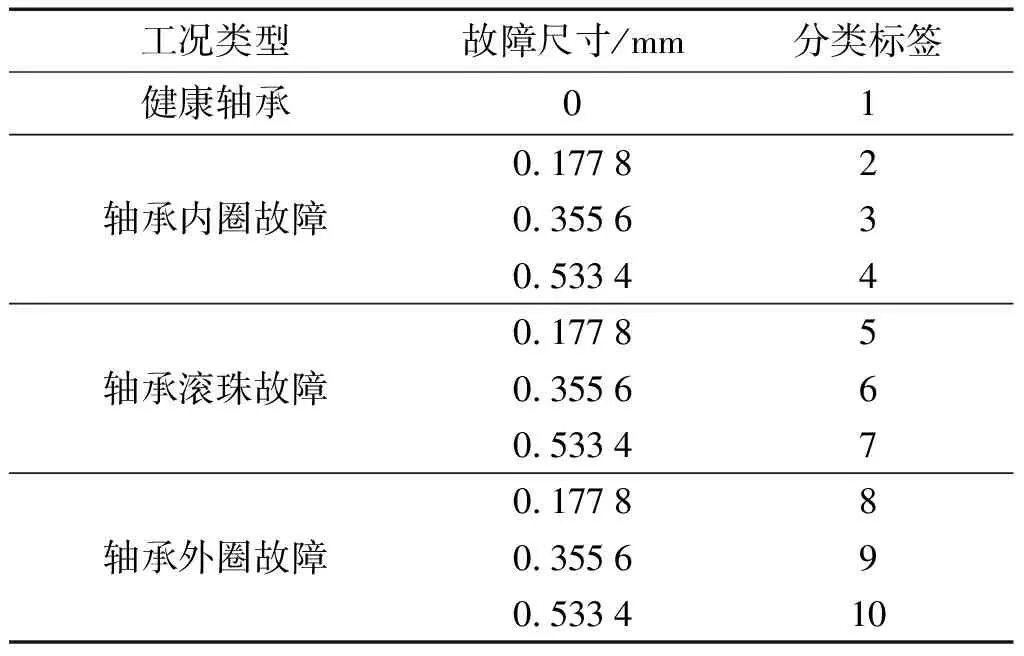
表1 滚动轴承实验数据信息

滚动轴承振动信号的时域波形如图7所示。

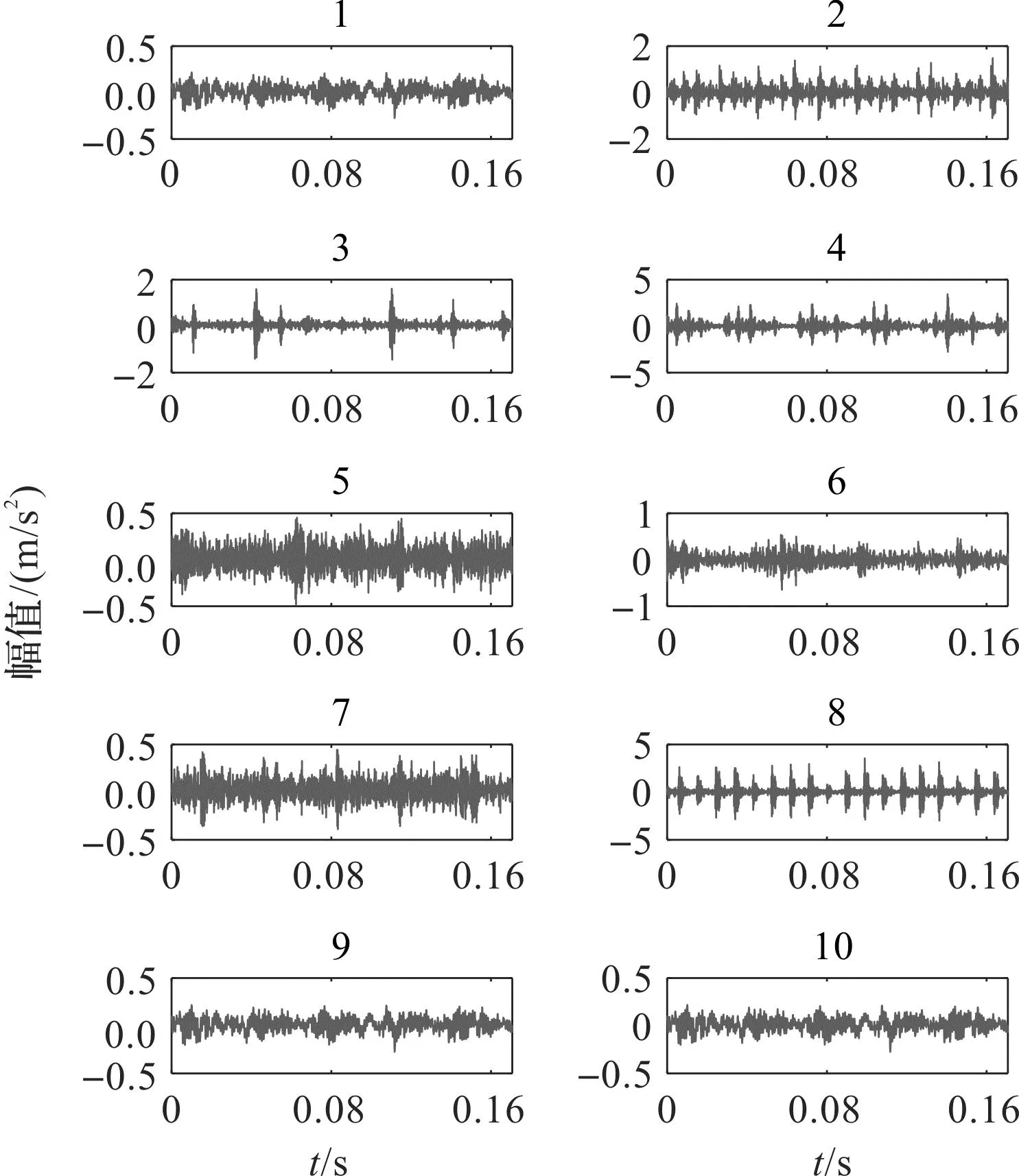
图7 滚动轴承不同工况的振动信号Fig.7 Vibration signal of rolling bearing under different working conditions

笔者采用HRFDE提取滚动轴承样本的故障特征,结果如图8所示。

图8 滚动轴承样本的HRFDEFig.8 HRFDE of rolling bearing samples

由图8可以看出:HRFDE具有良好的区分性能,不同节点上各个样本具有较好的区分度,没有出现明显的混叠,证明HRFDE能够从滚动轴承中提取出高质量的故障特征。此外,还可以发现在尺度因子为1时,健康样本的HRFDE值明显大于其它故障样本,且差异较大,这表明反向波动散布熵可以用于检测轴承是否有故障,并设定阈值。

4.1.2 方法有效性验证

为了进一步识别滚动轴承的故障类型和严重程度,并判断HRFDE方法的有效性,笔者将提取的HRFDE故障特征输入至GSA-PNN分类器中,进行训练和测试,得到了故障的识别结果和其混淆矩阵,如图9所示。

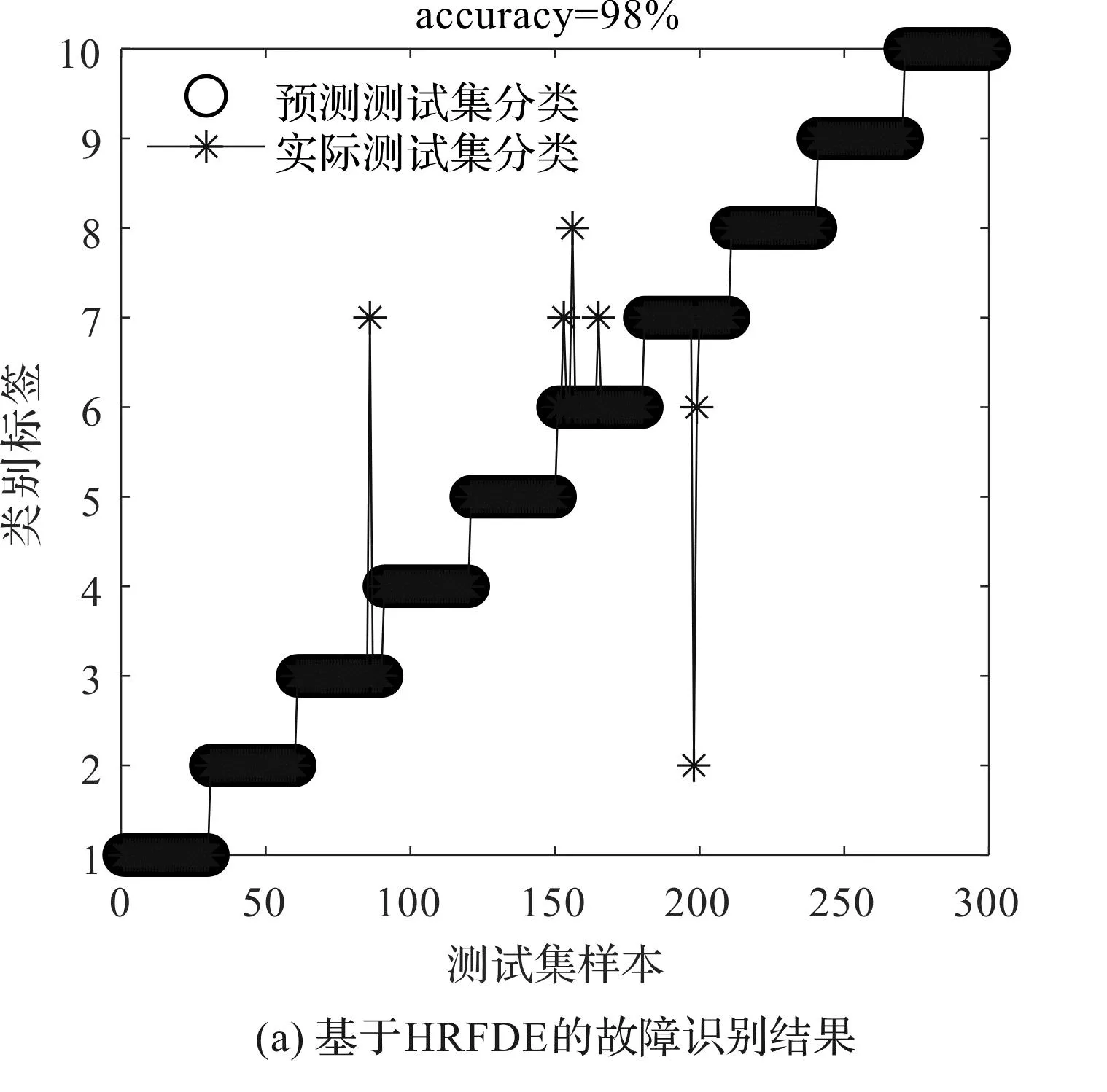
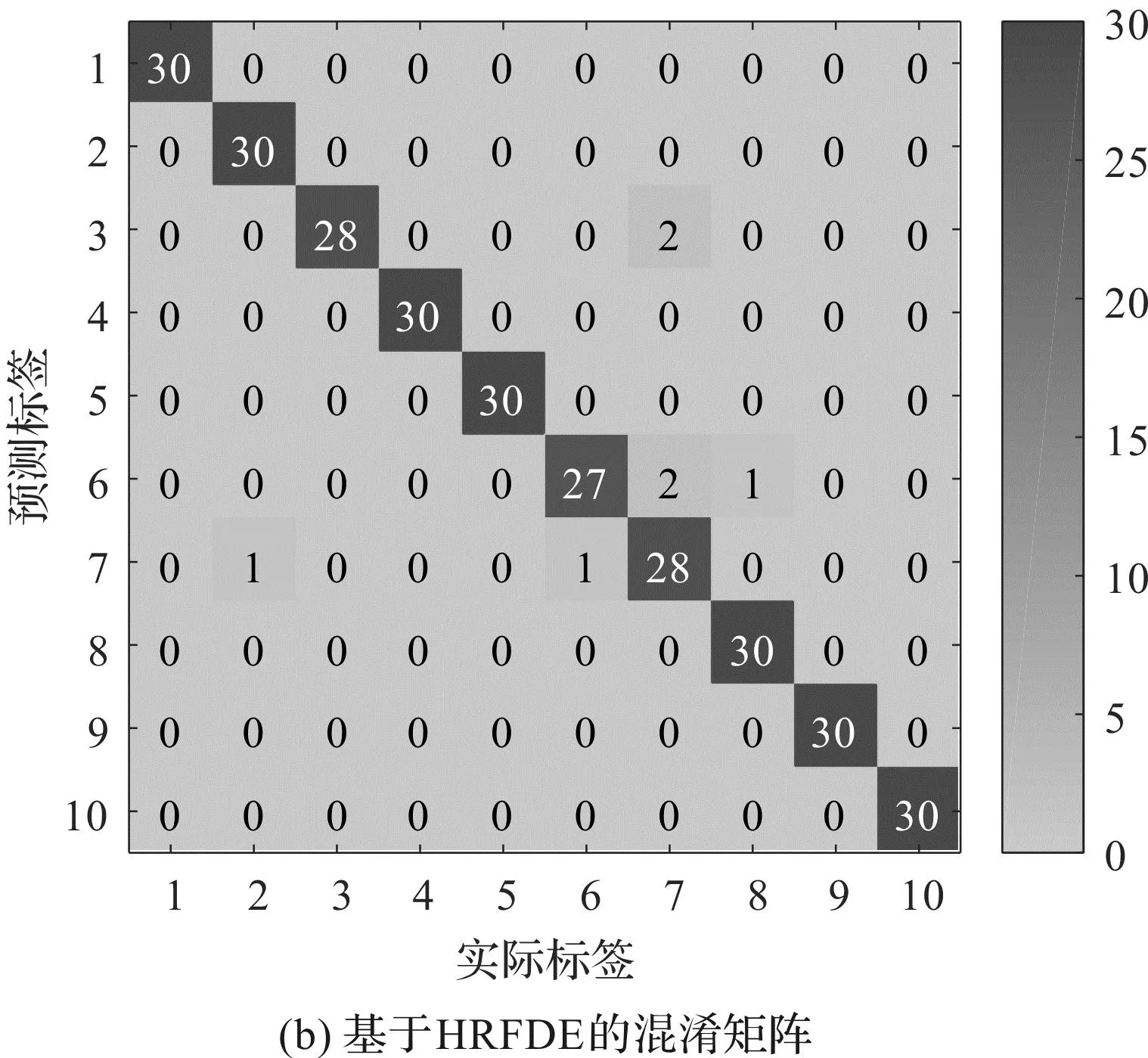
图9 基于HRFDE和GSA-PNN的故障识别结果和混淆矩阵Fig.9 Fault identification results and confusion matrix based on HRFDE and GSA-PNN

从图9可以发现:采用基于HRFDE与GSA-PNN的故障诊断方法取得了98%的故障识别准确率,有6个样本被错误地识别为其他类型:

2个轴承内圈故障(故障直径0.355 6 mm)被错误识别为轴承滚珠故障(故障直径0.533 4 mm);3个轴承滚珠故障(故障直径0.355 6 mm)中有2个被错误识别为轴承滚珠故障(故障直径0.533 4 mm),另外1个被错误识别为轴承外圈故障(故障直径0.177 8 mm);有2个轴承滚珠故障(故障直径0.533 4 mm)被分别错误识别为轴承滚珠故障(故障直径0.355 6 mm)和轴承内圈故障(故障直径0.177 8 mm)。

总之,基于HRFDE和GSA-PNN故障诊断方法具有良好的性能,其能够精准地诊断滚动轴承不同故障类型和严重程度的故障。

4.2 齿轮箱故障诊断实验

由于凯斯西储大学轴承数据是在较为理想的状态下采集得到的,因此,无法充分验证基于HRFDE与GSA-PNN的故障诊断方法的通用性和有效性。

4.2.1 故障数据来源

为此,笔者采用江苏千鹏故障诊断有限公司提供的齿轮箱故障实验数据,进行算法的有效性和泛化性验证。

齿轮箱故障模拟实验平台如图10所示。

图10 齿轮箱故障模拟实验平台Fig.10 Gear box fault simulation test platform

该平台由原动机、轴承、齿轮箱、制动器和多个传感器组成。笔者对传感器4所采集的振动信号进行分析。其中,齿轮箱中包含一个大齿轮和一个小齿轮,材料为S45C,通过油浸的方式进行润滑。

齿轮的参数如表2所示。

表2 齿轮的关键参数

齿轮箱数据集由5种工况下的振动信号组成,即健康齿轮、齿轮磨损、齿轮断齿、齿轮点蚀和齿轮点磨(大齿轮点蚀、小齿轮磨损)。其中,齿轮点磨为复合故障,笔者替换齿轮箱中的齿轮来模拟不同的齿轮故障。

笔者将传感器的采样频率设置为5.12 kHz,转速设为880 r/min。5种工况的齿轮箱信号被均匀地分割为50组长度为2 048的样本,共250组样本。其中,每种工况随机抽取30组数据作为训练集,剩余20组数据作为测试集。

实验样本的详细信息如表3所示。

表3 齿轮箱样本的详细信息

齿轮箱振动信号的波形如图11所示。

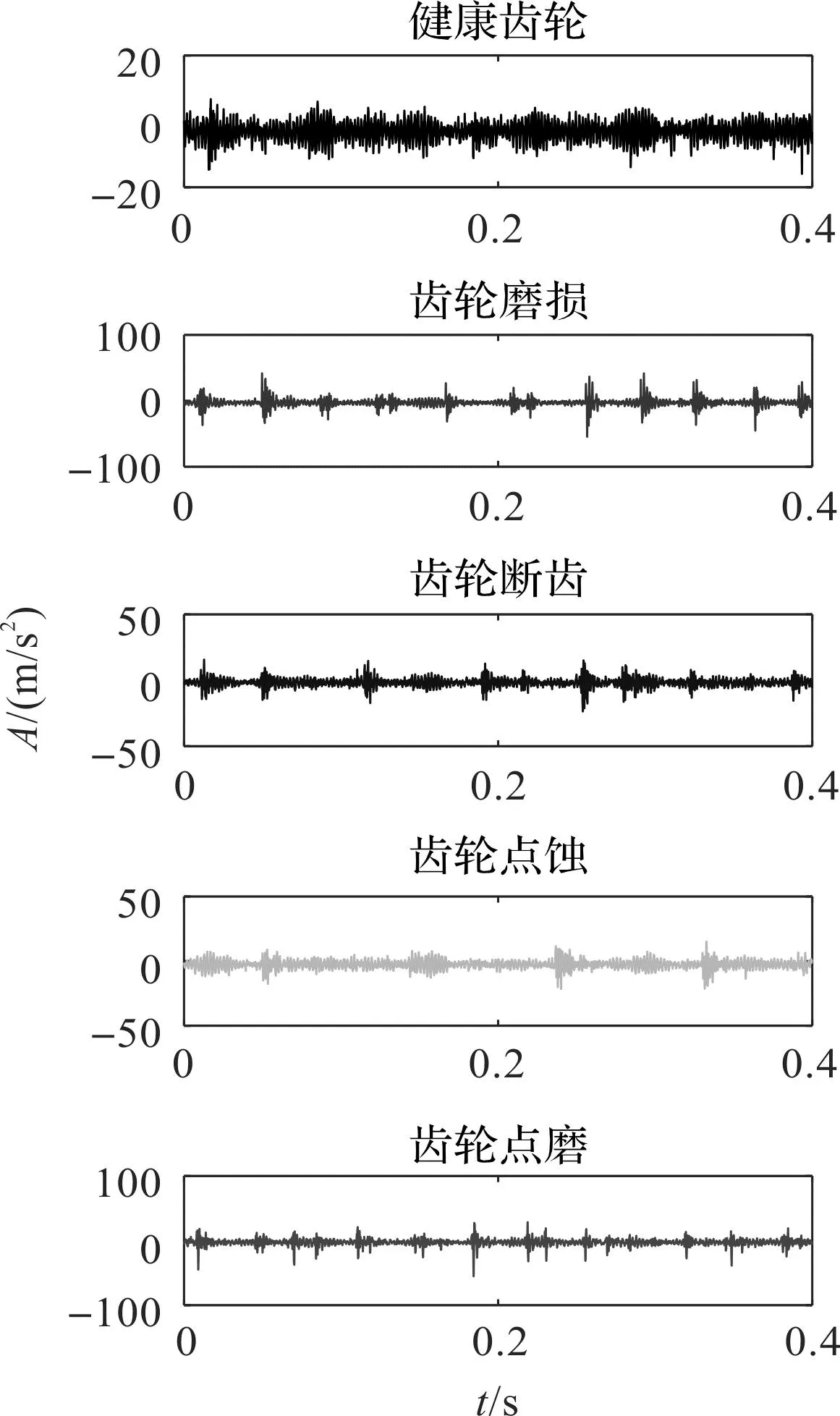
图11 齿轮箱振动信号的波形Fig.11 Waveform of gear box vibration signal

首先,笔者对每个样本进行HRFDE分析,提取前8个节点的熵值作为故障特征。

4.2.2 方法优越性验证

为了验证基于HRFDE与GSA-PNN的故障诊断方法的优越性,笔者将该方法与MRFDE、MFDE、HDE进行比较。4种方法的参数设置保持一致,即嵌入维数m=2,类别数c=5,时间延迟d=1。

采用不同方法得到的每种类型数据的均值如图12所示。

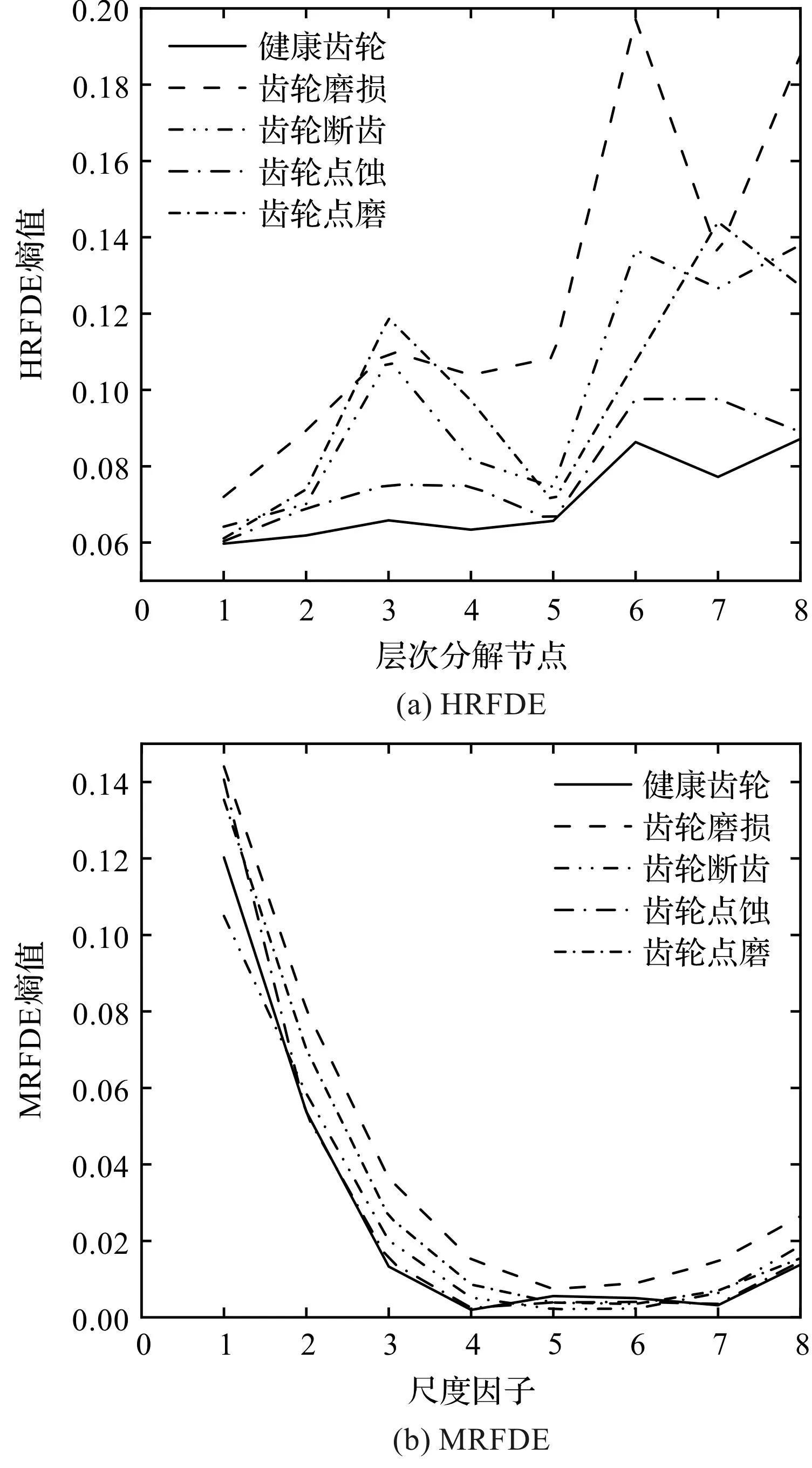
由图12可知:HRFDE和HDE对样本的区分度最佳,因为这2种方法能够充分地提取信号中的高频特征信息,因此特征质量更好;而MRFDE和MFDE的熵值曲线出现了明显的混叠,难以有效区分各个故障类型。

总之,在一定程度上,笔者可以根据熵值曲线判断HRFDE方法优于MRFDE和MFDE,但无法准确评估和HDE的优劣,需要结合GSA-PNN分类器进行故障识别,以更准确地评估HRFDE算法的有效性。

4.2.3 特征提取能力对比

为了评估4种方法的特征提取性能,并判断故障的类型,笔者利用训练完备的GSA-PNN多故障分类器对测试样本进行识别,并得到了最终的诊断结果和混淆矩阵,如图13所示。

从图13可以发现:基于HRFDE和GSA-PNN的故障诊断方法取得了98%的识别准确率,较为准确地诊断了齿轮箱的不同故障。

为了更加直观地观察4种方法的差异,笔者统计了不同方法进行故障诊断时的诊断准确率、错误识别数量和特征提取时间,得到采用不同方法的具体诊断

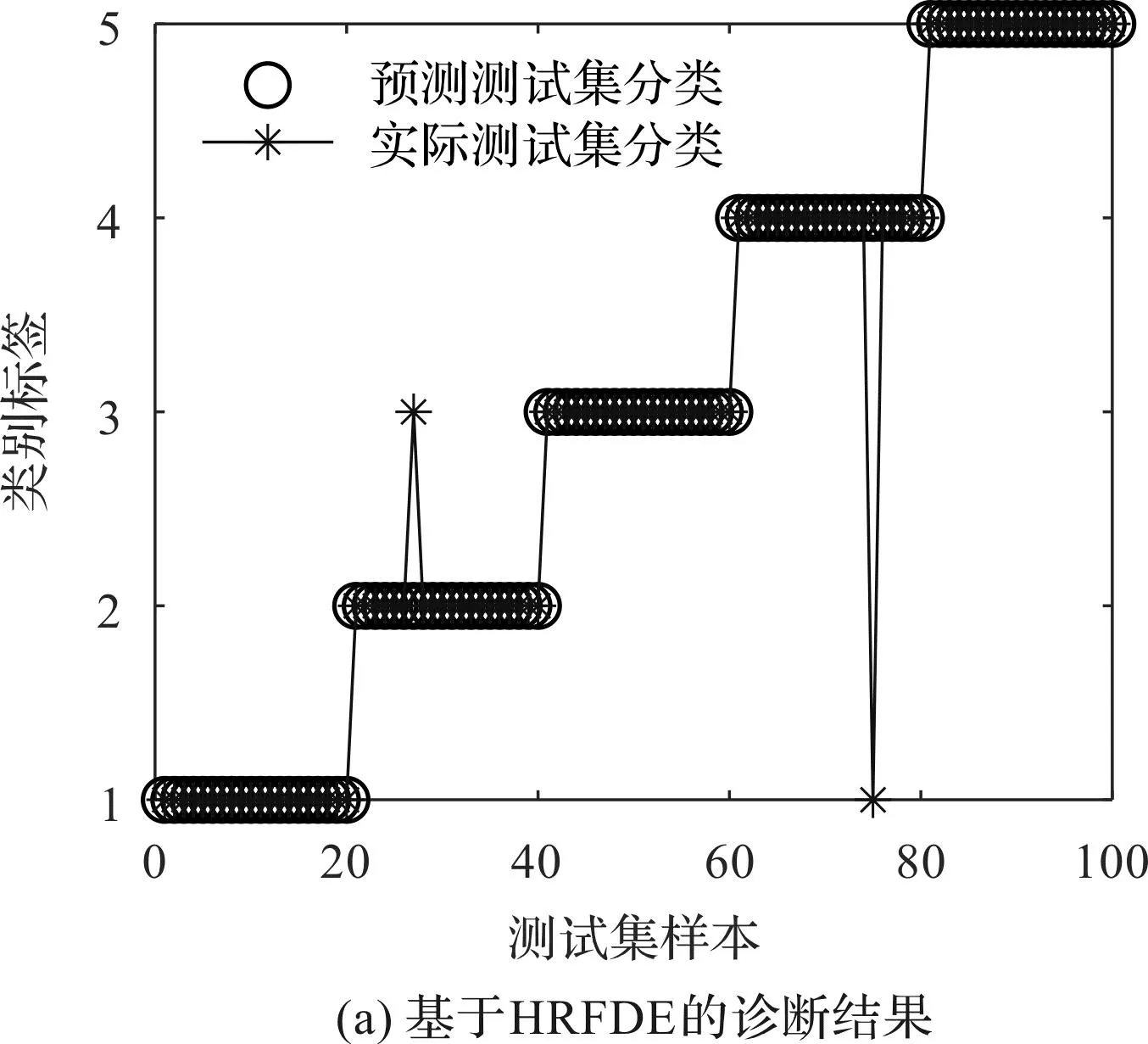
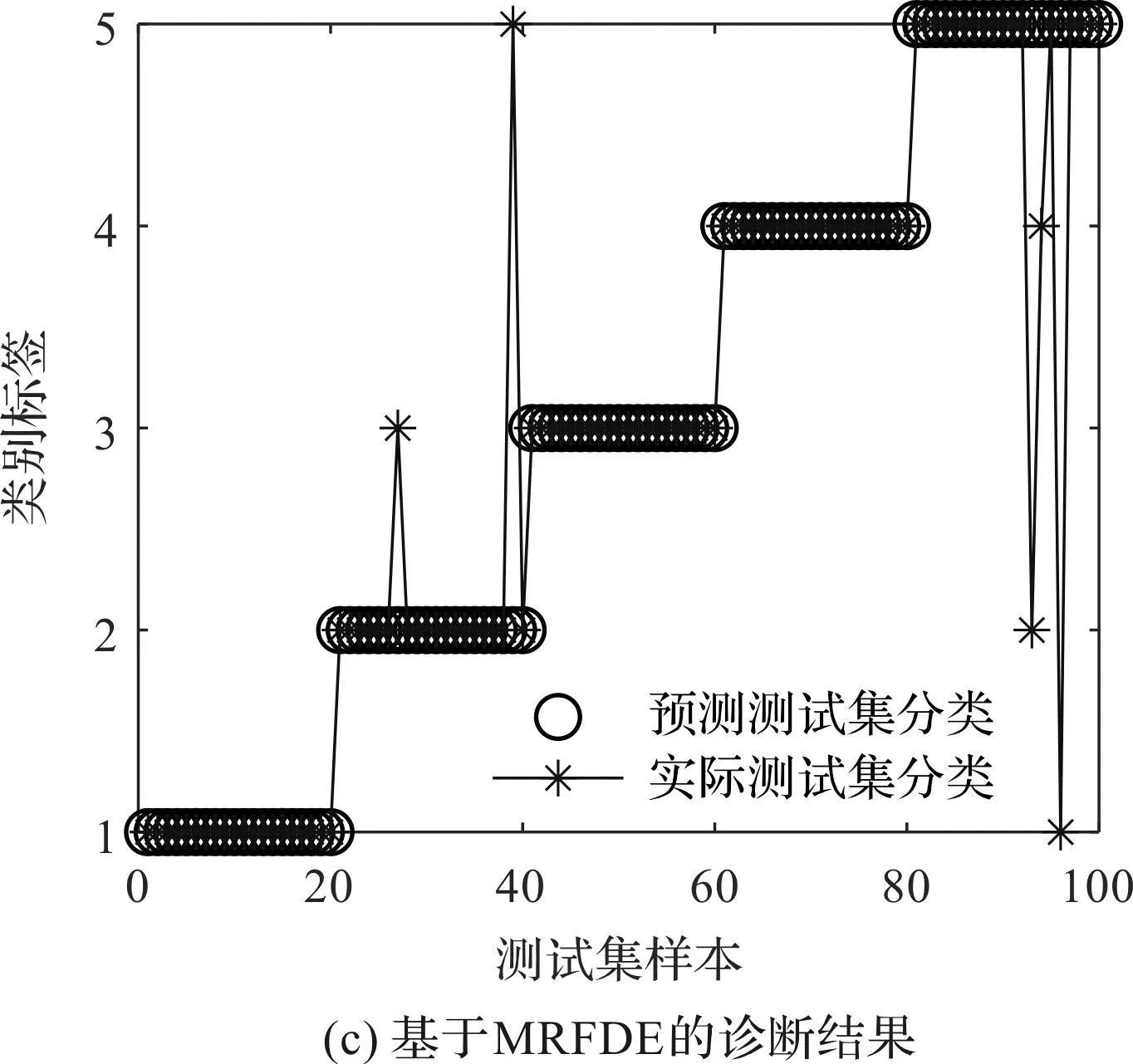
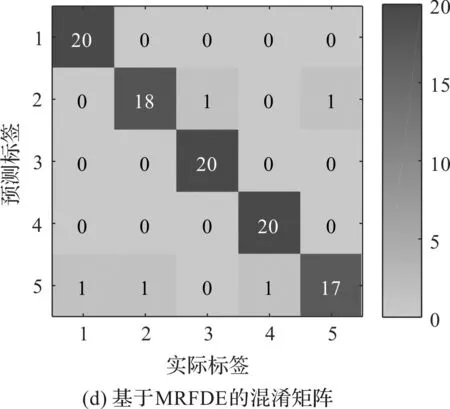
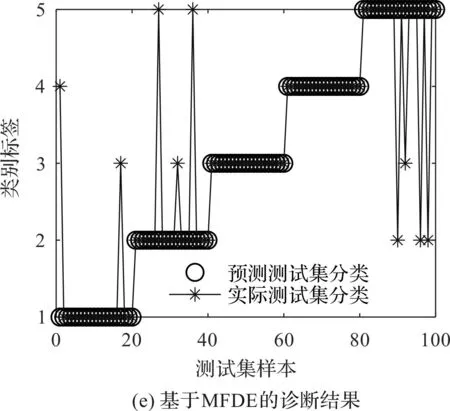
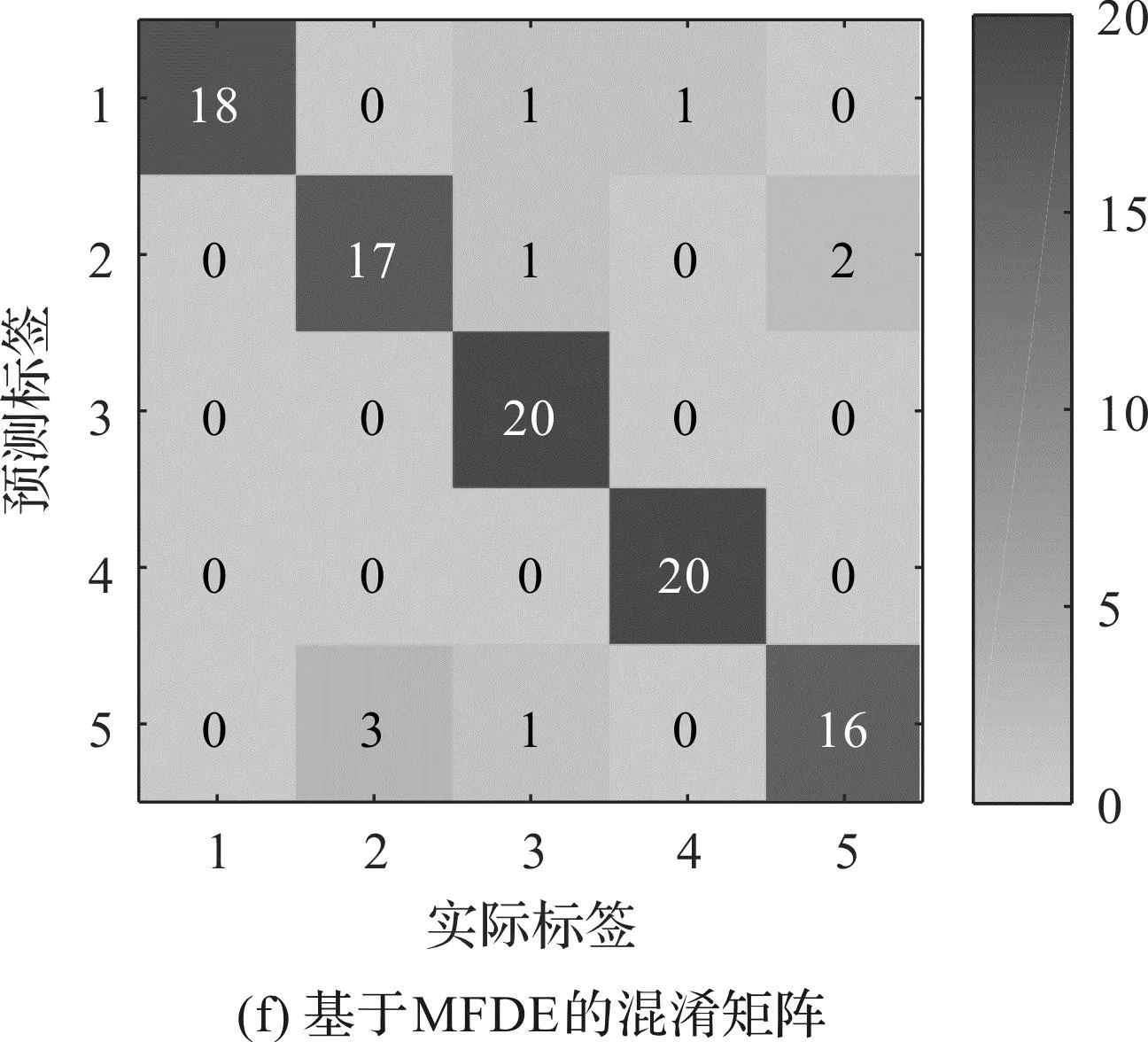
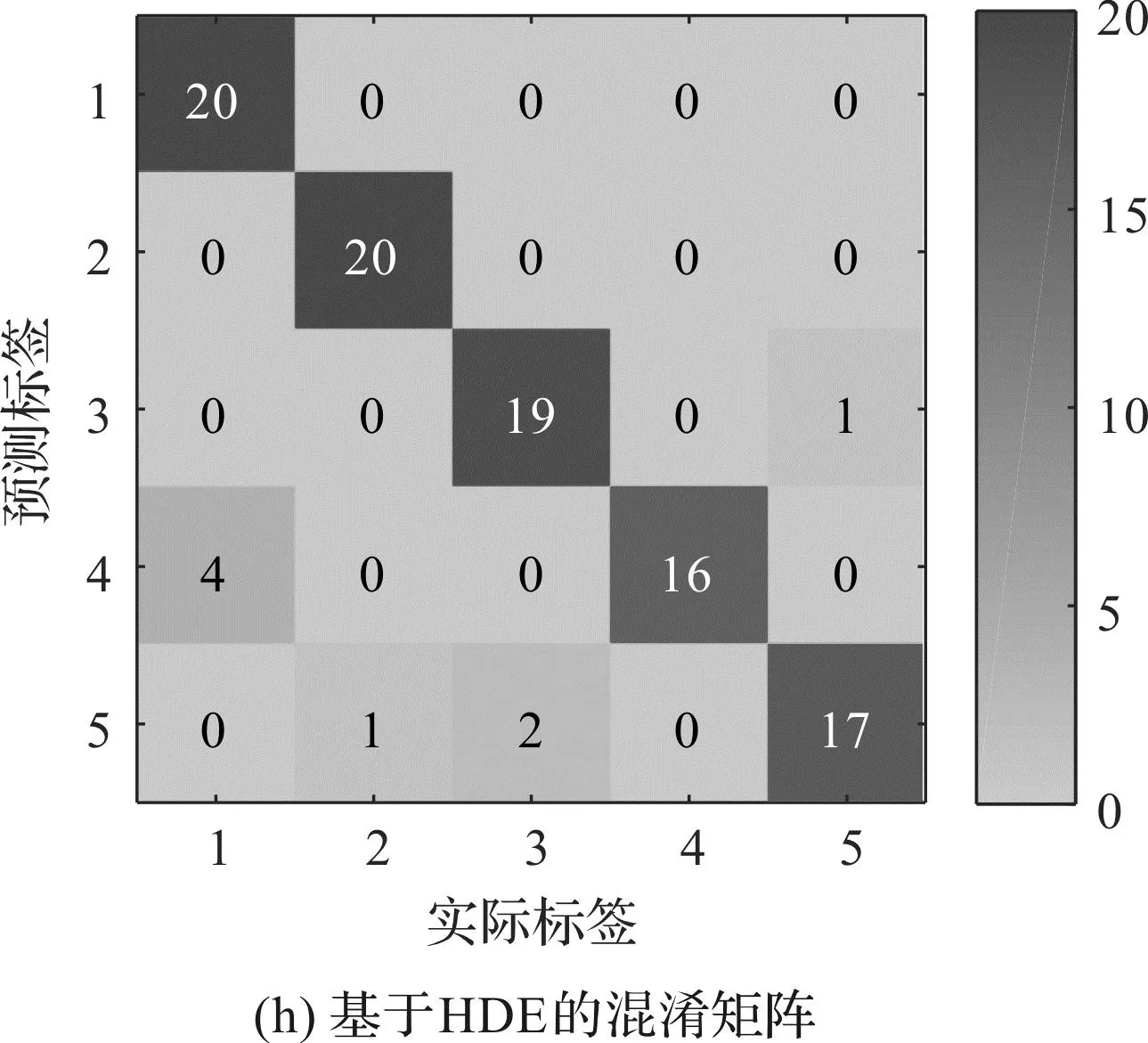
图13 基于4种故障诊断方法的GSA-PNN诊断结果和混淆矩阵

结果,如表4所示。

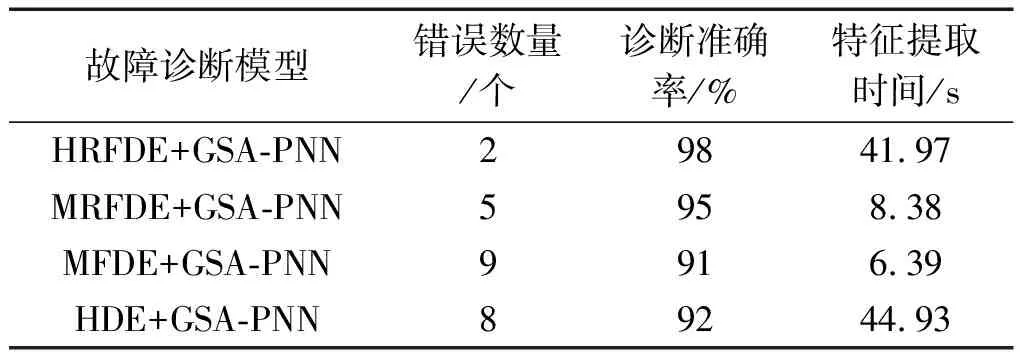
表4 不同方法的具体诊断结果

结合图13和表4可知:HRFDE+GSA-PNN方法的准确率最高,证明了该方法在特征提取中的优越性;该方法的效率高于HDE+GSA-PNN,低于MRFDE+GSA-PNN和MFDE+GSA-PNN,但其仅需要41.97 s即可完成故障特征的提取,具有比较高的效率。

综上可知,该方法具有比较优异的性能。

由表4还可以发现,上述4种方法的准确率较为接近。

4.2.4 方法的稳定性评估

为了进一步对HRFDE+GSA-PNN方法的有效性(稳定性)进行评估,笔者重复进行了5次实验,得到了5次实验下各方法的诊断结果,如图14所示。

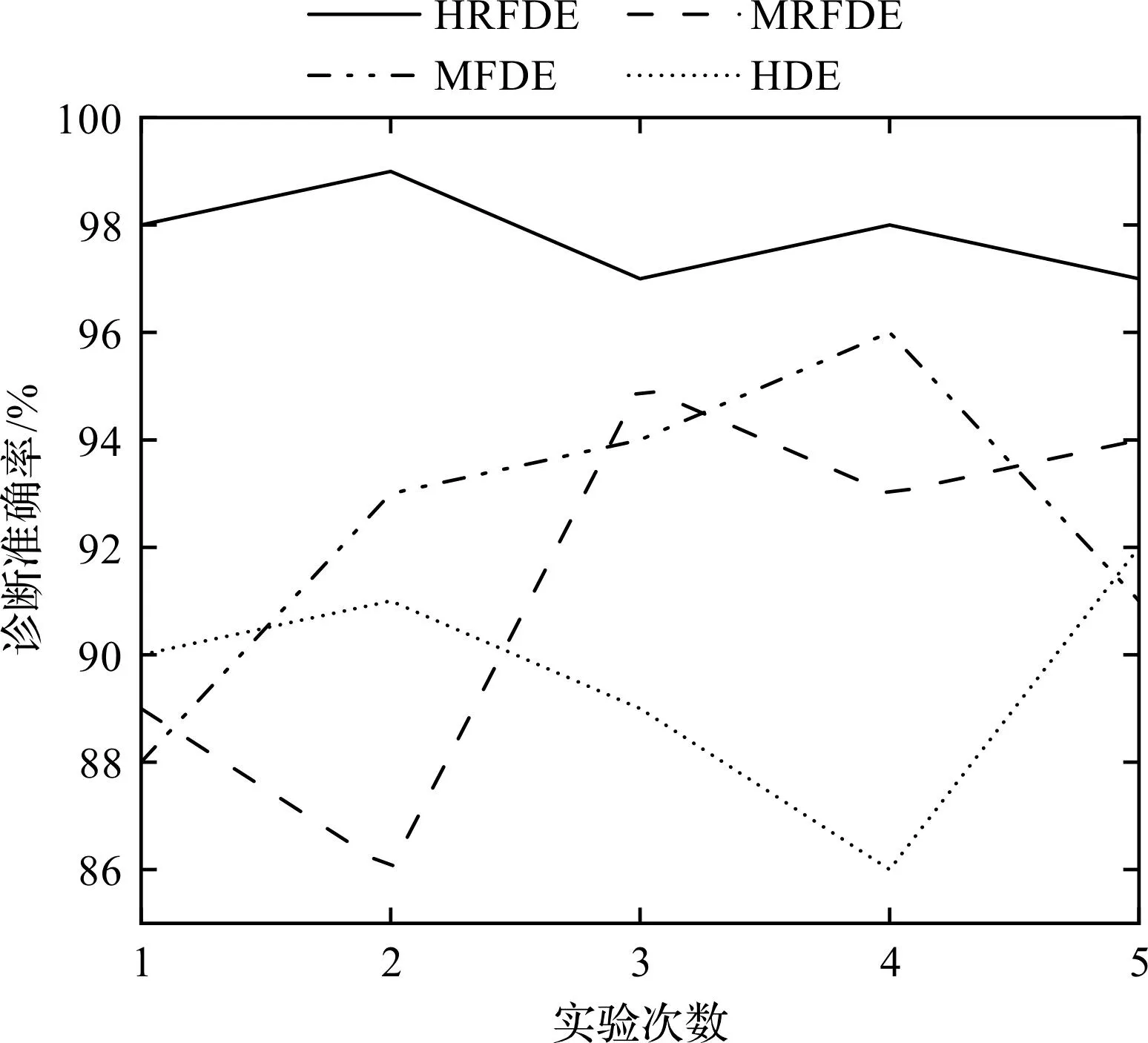
图14 5次实验下各方法的诊断结果Fig.14 The diagnostic results of each method under five experiments

由图14可以发现:经过多次实验,HRFDE+GSA-PNN方法的诊断准确率均高于其他3种方法,证明了该方法具有极强的稳定性。

同时,该方法的每次诊断准确率均高于95%,说明其能够准确地诊断齿轮箱的故障。

5 结束语

针对旋转机械的故障识别问题,笔者提出了一种基于HRFDE和GSA-PNN的旋转机械故障诊断方法,并利用两种旋转机械数据集分别进行了实验,证明了该方法的有效性和优越性。

研究结论如下:

1)HRFDE能够较为准确地刻画时间序列中的高频特征信息,白噪声信号的HRFDE标准差均小于MRFDE的标准差,证明了HRFDE相对于MRFDE更稳定;

2)将HRFDE用于旋转机械故障数据分析,结果表明,HRFDE能够从振动信号中提取较高质量的特征,可靠地区分了旋转机械的各个故障状态,识别准确率均达到了98%;

3)建立了一种基于HRFDE和GSA-PNN的旋转机械故障诊断方法,并基于两种数据进行了分析评估,结果表明:该方法的分类准确率达到了98%,而特征提取时间为41.97 s,其综合性能要优于MRFDE、MFDE和HDE方法。

当前,笔者在使用HRFDE方法进行旋转机械的故障识别时,没有考虑其故障特征中的冗余,因此,后续笔者将结合特征选择算法对HRFDE特征进行优化筛选。