基于遗传算法的多级主压阀动态特性优化

王璇，王殿鑫，姜宏暄，刘洋，刘丽芳，杨庆俊

(1.哈尔滨工业大学机电工程学院，黑龙江哈尔滨 150000；2.中国北方车辆研究所，北京 100071；3.中国人民解放军63963部队，北京 100072)

0 前言

液力自动变速器能够使工程车辆获得很好的起步加速性能，提高车辆自主适应复杂道路的能力，在重型工程车辆中应用广泛。液力自动变速器的换挡操纵、换挡控制、润滑等都依赖液压控制系统[1-2]。主调压阀在液力自动变速器液压控制系统中发挥重要的作用。李红等人[3]提出一种基于试验设计-遗传算法的优化方法，用于处理多变量交互作用下电磁阀响应特性优化问题。张立强等[4]通过Kriging代理模型对正交设计结果进行曲面插值后，利用遗传算法对Kriging代理模型求取最优值，实现闸阀阀体强度及其密封性能优化。郏云涛、田俊[5]通过遗传算法和经验试凑法整定PID控制器参数，并对仿真结果进行对比分析。李胜永[6]基于遗传算法和序列二次规划方法，对相同优化参数区间的优化结果进行了对比分析，进行了优化参数区间对遗传算法优化结果的影响分析。郑王刚等[7-8]采用改进遗传算法优化RBF神经网络结构，通过MATLAB软件对双步进电机伺服阀改进的控制系统进行仿真验证，能够抑制外界的干扰，从而提高双步电机伺服阀控制系统的响应速度和输出精度。

综上所述，一般在对阀进行结构参数优化时，大多都是凭借经验对某些参数逐个调整，最后通过实验进行验证。该方法在实际中对阀性能有一定的改善，但不能保证阀的性能最优[9]。因此，采用优化方法对阀进行性能优化很有必要。遗传算法是一种借鉴生物界自然选择和自然遗传机制的随机搜索算法[10]，具有全局搜索性能，也不需要辅助信息，因此具有很强的实用性。本文作者利用MATLAB优化工具箱[11-12]中提供的遗传算法与Simulink结合对多级主调压阀的动态性能进行优化，提高多级主调压阀的快速性。

1 多级主调压阀动态数学模型

多级主调压阀结构如图1所示。进油口油压为主油压，反馈腔1、2、3分别与阻尼孔1、2、3接通。阀芯采用阶梯轴，通过控制主油压进入不同的反馈腔1、2、3可使主调压阀输出不同的主油压。当只有反馈腔1接入时，调定压力为2.0 MPa；当只有反馈腔1和3同时接入时，调定压力为1.6 MPa；当反馈腔2与反馈腔1和3同时接入时，既可以改善主调压阀入口主油压的波动，又可以与反馈腔1和3配合使主调压阀调定的压力进一步降低实现多级压力调节。

图1 多级主调压阀结构示意

为简化起见，忽略阀芯与阀体配合之间的泄漏量，动态数学模型可用下列方程表示。

(1)流量压力方程

①溢流回液力变矩器阀口处流动方程

(1)

②溢流回油箱阀口处流动方程

(2)

式中：Q1、Q2为对应阀口流量；cd为阀口流量系数；w为面积梯度；ps为主油压力；p1为液力变矩器口压力；x为阀芯位移；ρ为液压油密度；x0为溢流回油箱阀口处阀芯的遮盖长度。

③阻尼孔压力流量方程

为了减小油液黏度对阻尼孔流动的影响，反馈腔1、2、3采用的阻尼孔为薄壁小孔。阻尼孔满足流量特性公式

(3)

式中：Q为阻尼孔流量；A为阻尼孔通流面积；Δp为阻尼孔前后压力差。

(2)流量连续性方程

①反馈腔1流量连续性方程

考虑流体的可压缩性，流入反馈腔1的流量为

(4)

式中：A1为反馈腔1的有效面积；Vc1为反馈腔1的有效体积；βe为油液性模量。

同理，流入反馈腔3的流量为

(5)

式中：A3为反馈腔3的有效面积；Vc3为反馈腔3的有效体积。

②多级主调压阀入口受控腔连续性方程

当油液溢流到液力变矩器和油箱时，考虑流体的可压缩性，对受控腔有：

(6)

式中：Qp为操纵油泵的输出流量；Ql为负载流量；Vt为受控腔的有效体积。

当油液只溢流给液力变矩器时，对受控腔有：

(7)

(3)阀芯受力平衡方程

(8)

式中：FRS1为液力变矩器阀口处稳态液动力；FRS1=-2cdcvw(ps-p1)cosθ；FRS2为回油箱阀口处阀芯受到的稳态液动力，FRS2=-λ·2cdcvwps(x-x0)cosθ，λ为阀口稳态液动力补偿系数；Bc为等效黏性阻尼系数；F0为弹簧的预紧力；K为弹簧刚度；Fc为阀芯所受库仑摩擦力绝对值；m为阀芯质量。

(9)

通过以上建立的多级主调压阀非线性数学模型即可对阀的动态特性进行分析。

2 多级主调压阀动态特性仿真

建立多级主调阀的Simulink动态仿真模型如图2所示，主要仿真参数如表1所示。子系统模型包括阀溢流回液力变矩器阀口处稳态液动力和流量模型、溢流回油箱阀口处稳态液动力和流量模型、反馈腔1压力模型、阻尼孔1流量模型、反馈腔3压力模型、阻尼孔3流量模型、阀芯动力学模型。反馈腔3接通与否是通过换向电磁阀来实现的，因此通过两个函数模块对反馈腔3的压力和流量进行控制。

表1 多级主调压阀主要仿真参数

图2 多级主调压阀Simulink模型

2.1 结构参数对动态特性的影响

以阶跃流量输入，分析阀入口压力响应情况，给多级主调压阀入口阶跃流量加一时间常数T=0.012 5 s的一阶惯性环节。通过改变结构参数，分析各结构参数对多级主调压阀入口压力动态特性的影响。图3—8分别为阻尼孔1直径、受控腔体积、弹簧刚度、阀芯质量、阻尼孔3直径和液动力对主压阀对动态特性的影响。

由图3可知：随着阻尼孔1直径的增大，在遭遇负载突变时，主压阀的压力下降幅度减小，压力稳定时间减小，且压力恢复时产生的冲击减小。阻尼孔1直径对主调压阀入口压力的动态性能影响显著。

由图4可知：阻尼孔1直径保持为0.5 mm，受控腔体积应由阀结构确定，随着受控腔体积的增大，主调压阀压力稳定时间与定压精度基本不变。根据理论分析，受控腔体积增大对压力的响应速度影响不大是由于增加的体积有限，因此对响应速度的影响有限。

图4 受控腔体积Vt对主压阀动态特性的影响

由图5可知：当阻尼孔1直径为0.5 mm、受控腔体积为60 cm3时，面临负载突变，随着弹簧刚度的增大，主压阀的压力跌落减小，但恢复时的压力冲击增大，压力稳定时间基本不变；并且随着弹簧刚度的增加，主压阀的稳定压力受到影响，弹簧刚度越大，阀稳定时的压力越大。因此，多级主调压阀弹簧刚度应进行综合考虑。

图5 弹簧刚度K对主压阀对动态特性的影响

由图6可知：当阻尼孔1直径为0.5 mm、受控腔体积为60 cm3、弹簧刚度为12 N/mm时，改变阀芯质量时，随着阀芯质量的增大，阀在面临负载突变时，压力跌落增大，但质量超过0.3 kg后，压力跌落几乎不再有变化；阀入口调定压力最大超调量增大，但阀芯质量超过0.3 kg后，最大超调量不再增加。可以看出质量对阀的压力稳定时间影响很小，阀芯质量应该由阀结构确定。

图6 阀芯质量m对主压阀动态特性的影响

由图7可知：阻尼孔3直径d3对多级主调压阀不同调定压力切换过程的动态特性几乎没有任何影响，因此在使用时阀反馈腔3不安装阻尼孔。

图7 阻尼孔3直径d3对主压阀动态特性的影响

当阻尼孔1直径为0.5 mm、受控腔体积为60 cm3、弹簧刚度为12 N/mm、阀芯质量为0.3 kg时，改变液动力大小，由图8可以看出：在负载变化时，随着液动力的增大，主压阀的压力冲击变化不大，压力超调量变化不大，压力稳定时间略有减小。但不进行液动力补偿时，主压阀的稳定压力不在稳压精度要求范围内，故进行液动力补偿是必要措施。综合考虑定压精度与压力稳定时间，确定液动力补偿50%能得到最优性能。

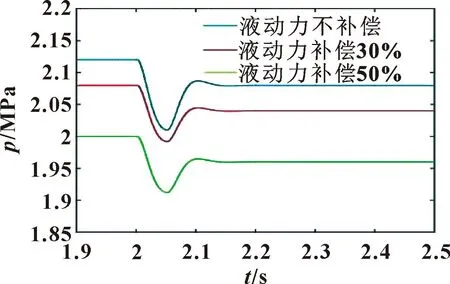
图8 液动力对主压阀动态特性的影响

2.2 多级主调压阀优化数学模型的建立

将ISE准则(平方误差积分准则)作为多级主调压阀动态性能优化的设计准则。ISE准则的数学表达式为

(10)

式中：e(t)表示多级主调压阀入口的实际压力值与期望压力值的偏差；t为时间。为获得更优的动态性能，用相对误差来代替绝对误差，相对误差为

(11)

式中：ps为阀入口的实际压力值；pc为阀入口的稳态压力值。

通过多级主调压阀各结构参数对阀入口压力动态响应特性影响的大小分析，选取弹簧刚度、弹簧预压缩量、阻尼孔1的直径等对阀入口压力影响较大的参数作为待优化变量。根据参数变化对阀入口压力影响的趋势，确定了一个优化范围。多级主调压阀优化的目标函数为

(12)

约束条件为

(13)

3 遗传算法参数优化

MATLAB优化工具箱提供的遗传算法是使目标函数最小，即适应度函数是求目标函数的最小值。适应度函数的计算是通过M文件实现的，文中设计的多级主调压阀非线性动态仿真模型是在Simulink中搭建的，因此需要将目标函数在Simulink表示出来，并将输出值返回给M文件。优化过程需要Simulink和M文件进行数据交互，首先遗传算法将产生的参数传递给Simulink进行仿真，将仿真得到的目标函数的函数值返回给M文件，遗传算法根据返回的结果对参数进行调整，不断进行仿真和优化。多级主调压阀结构参数优化流程，如图9所示。

图9 多级主调压阀结构参数优化流程

在Simulink中将以ISE准则确定的目标函数以模块化的方式表示出来，如图10所示。

图10 ISE准则的Simulink模块表示

在对参数进行设置时，“Population size(种群尺度)”中每代种群中个体的数目取为50；elite count(优良计数)，设置为0.05倍种群尺度；Crossover fraction(交叉概率)，设置为0.8；“Number of variables(变量数目)”为3；“Bounds(界限)”下界为[8×103，0.3，20]、上界为[22×103，3.0，65]。

4 结果分析和实验验证

遗传算法优化结果如图11、12所示，可以看到，当遗传算法迭代到57代时优化停止，目标函数的变化量小于“Function tolerance(函数误差)”的设定值1×10-6。

图11 遗传算法结果

图12 各代适应度函数的最佳值适应度值与最佳个体

将得到的优化参数结果应用到结构中，对多级主压阀进行实验，其中K=14.314 N/mm，X0=35.43 mm，d1=1.77 mm，实验系统原理和实验台如图13所示。

图13 实验原理(a)和实验台现场(b)

图14为多级阀的静态压力-流量曲线，参数优化后，当多级主调压阀的溢流流量从30 L/min增大到约为150 L/min时，压力上升约0.18 MPa，静态性能良好。

图14 多级主调压阀静态压力-流量曲线

结构优化后，多级主调压阀入口调定压力在模拟换挡操纵系统离合器用油时的流量变化约为70 L/min，此过程反复切换进行实验，主压压力的曲线变化如图15所示。

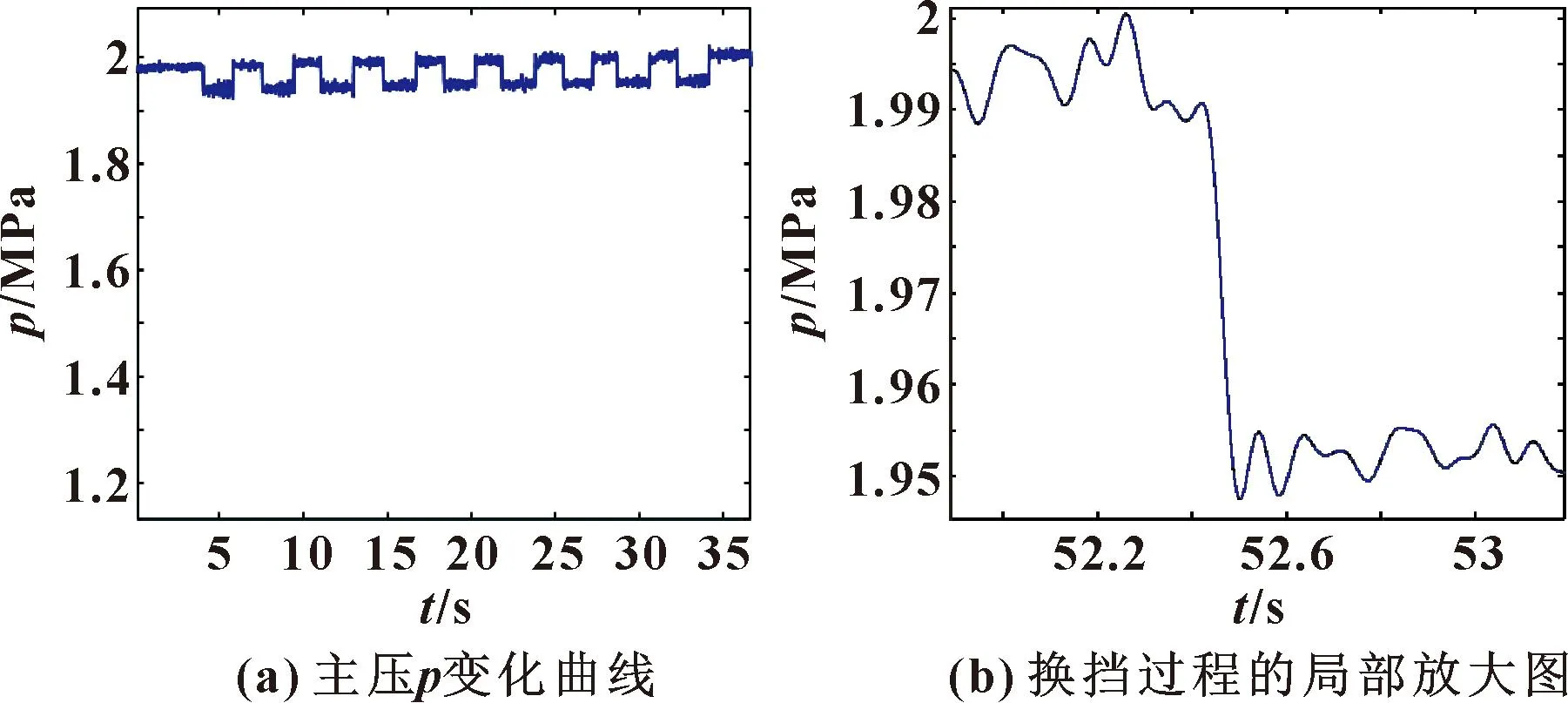
图15 离合器用油时多级主调压阀压力变化曲线对比

由图15可以看到：优化后的多级主调压阀在受换挡操作使得负载流量突增的影响下，压力降低小于定压压力的10%，调整时间小于200 ms，动态性能良好。

5 结论

分析多级主调压阀各结构参数对阀入口压力动态响应特性的影响，发现多级主压阀弹簧刚度、液动力和阻尼孔1的直径等对阀入口压力影响较大，因此，作者利用遗传算法对弹簧刚度、阻尼孔直径和液动力的取值进行了优化，当多级主调压阀使用遗传算法优化的参数后，静态特性良好，负载流量突增时的主压压力降低现象得到了改善，调整时间缩短，动态性能良好。