先导级带环形间隙阻尼的水压溢流阀的开发

金斌，高阳，孙电锋

(桂林航天工业学院机电工程学院，广西桂林 541004)

0 前言

水液压技术已经广泛应用在抗辐射装备、矿井开采装备、清洗装备、水辅成型装备、细水雾灭火装备、海水淡化、水处理、水下机械等[1-8]。作为液压传动介质的水与油液相比有其优点，如清洁、可再生、难燃等，但其缺点同样突出，如黏度低、蒸汽压力高、易腐蚀等[9-10]。 自二战结束后，美国海军非常重视阻燃介质液压传动的研究[11]。由于水介质较传统油压介质难燃，日本非常重视水液压元件的研究，自20世纪90年代已先后开发了水压比例阀、水压伺服阀、水压高速开关阀等水压元件，广泛应用在钢铁工厂等液压系统设备上[12-18]。欧洲工业化国家已经有水压泵、水压缸、水压阀开发并商用[19]。 可以说水压传动给急需要求改善液压系统的安全性能带来了新机遇。然而由于水的黏度较低，水压元件对偶摩擦副之间很难形成有效润滑膜，表现为润滑特性较差，很容易形成摩擦磨损，给水压元件的性能造成不良影响。针对这个问题，URATA等[11，20]开发了带有静压轴承的水压伺服阀，克服了润滑特性差的特点，实验结果表明所开发的水压伺服阀与商用油压伺服阀特性类似，可以用于水压系统。SUZUKI等[21-23]开发了主阀芯带有静压轴承的水压溢流阀和减压阀，以主阀芯环形间隙阻尼作为先导液阻，以通过主阀芯静压轴承的泄漏流量作为先导流量，实验结果表明所开发的水压溢流阀可以很好地消除主阀芯与阀套库仑摩擦力所引起的滞环。

然而上文提到的作者所开发的水压伺服阀、溢流阀、减压阀有一个共同的特点就是都设计了主阀芯静压轴承。该静压轴承的特点是结构较复杂、加工难度较大、加工成本较高。

针对上述问题，本文作者所研制的水液压溢流阀在充分考虑水的黏度比较低的基础上，设计了新的阀芯结构。

1 水压溢流阀工作原理及结构

1.1 水压溢流阀工作原理

所设计的水压溢流阀采用了先导级环形间隙阻尼结构。当先导级环形间隙结构充满流动介质时，一方面可作为先导级液阻，另一方面可充当先导级阀芯和阀套之间的润滑层来消除或降低它们之间的库仑摩擦力。

图1所示为带先导级环形间隙阻尼结构的水压溢流阀的工作原理。整个阀由两级组成：先导级用来调节阀的压力，主级用来调节阀的流量。先导级压力由伺服电机带动凸轮压缩弹簧来调节，伺服电机由数字控制卡来控制。

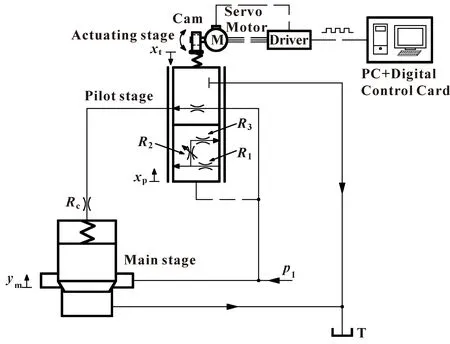
图1 水压溢流阀的工作原理

1.2 水压溢流阀结构

水压溢流阀先导级和主级的结构如图2—5所示。图2中，l0段和l5段的结构用来导向阀芯运动和阻止阀芯倾斜。I区和II区的细节分别如图3和图4所示。作为先导环形间隙阻尼的l1段和l3段的细节如图3和图4所示。4个直径为d的孔均布在先导阀芯四周，沟通A腔和环形间隙阻尼R1，如图3所示。

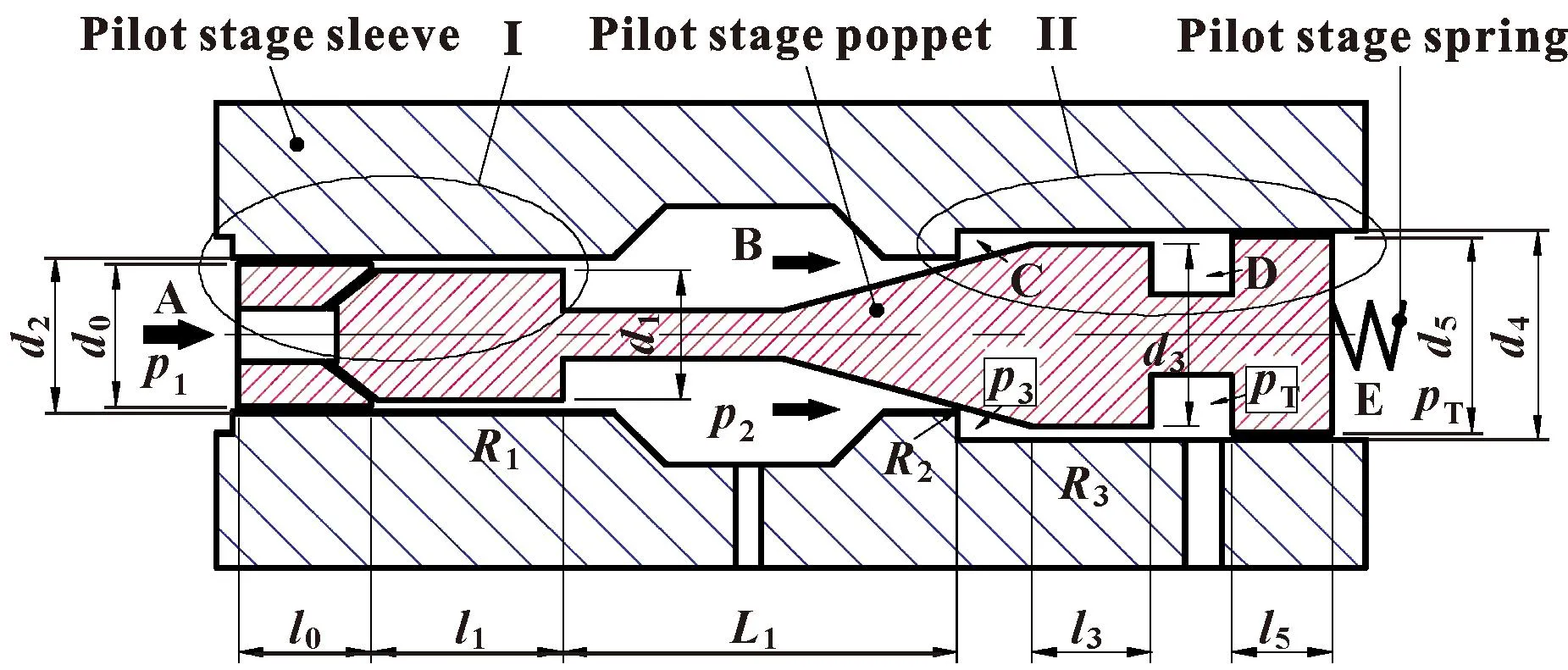
图2 带有环形间隙阻尼结构的先导级阀

图3 先导阀I区的细节

压力p1是由A腔的压缩流体所形成的，如图2所示。当p1作用在阀芯左端的液压力超过阀芯右端弹簧的调节力时，先导阀芯会向右移动，同时先导阀锥阀口打开，R2形成如图2所示。一旦先导节流口打开，A腔和B腔之间的压力差将不再是0，如图2所示。p1和p2之间足够的压力差会引起p1和主阀芯控制腔压力pm1之间的压力差形成，如图5所示。当作用在主阀芯上的压差力超过主阀芯上弹簧的作用力之后，主阀芯向左运动，主阀节流口打开，同时产生主阀流量qL，如图5所示。

所设计的水压溢流阀调节压力达14 MPa，最大流量达到80 L/min。本文作者推导和建立了所开发水压溢流阀的线性化数学模型和传递函数，通过理论和实验研究了所开发水压溢流阀的动态特性。

2 数学模型

为了分析先导阀带环形间隙阻尼的水压溢流阀的动态特性，推导了线性化数学模型，并作了如下假设：

(1)忽略阀芯和阀套的弹性变形；

(2)每个工作腔中的流体压缩量为0；

(3)先导阀芯的偏心被设为0，即ε=0；

(4)剪切力也忽略不计，因为它们远小于环形间隙阻尼中的压差力；

(5)通过环形间隙阻尼和细长孔的流体处于层流状态。

2.1 水压溢流阀基本流量方程

流量方程建立的初始条件为：压力为14 MPa。建立所开发水压溢流阀的线性化流量方程和流量连续性方程来研究阀的动态特性。

基于上面提到的最后两个假设，通过环形间隙阻尼R1的流量可以表示为

q1=C1(p1-p2)

(1)

通过先导锥阀液阻R2的线性化流量方程可以表示为

q2=C2xp

(2)

基于假设，通过环形间隙阻尼R3的流量可以表示为

q3=C3(p3-pT)

(3)

液阻Rc设计成长度是其直径4倍的细长孔，通过液阻Rc的流量可表示为

qc=Cc(pm1-p2)

(4)

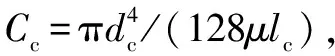
通过主阀锥阀的线性化流量方程可以表示为

qL=CLym

(5)

通过包括先导阀和主阀整个阀的流量可以表示为

qv=q1+qL

(6)

流量q1、q2和qc之间的平衡方程可以表示为

q2=q1+qc

(7)

不考虑C腔流体压缩性的流量q2和q3之间的平衡方程如图4可以表示为

q3=q2

(8)

不考虑F腔流体压缩性，通过液阻Rc的流量如图5可表示为

(9)

不考虑G腔流体压缩性，通过间隙液阻Rm3的流量如图5可表示为

(10)

qm3=Cm3(pT-pm3)

(11)

2.2 水压溢流阀力平衡方程

为了研究水压溢流阀的动态特性，建立了动态力平衡方程。先导级阀芯的动态力平衡方程表示为

A1p1+(A2-A1)p2+(A3-A2)p3-A3pT-Fpt-Fps=

(12)

(12.1)

式(12)中Fpt是作用在先导阀芯上的瞬态液动力，其线性化方程可以表示为

(12.2)

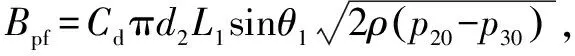
式(12)中Fps是作用在先导阀芯上的稳态液动力，其线性化方程可以表示为

Fps=Cpxp

(12.3)

式中：Cp=CvCdπd2sin(2θ1)(p20-p30)，是作用在先导阀芯上的稳态液动力系数；Cv是速度系数。

主级阀芯的动态力平衡方程可以表示为

Ammp1+Am3pm3-Am1pm1+Fmt-Fms=

(13)

(13.1)

式(13)中Fmt是作用在主级阀芯上的瞬态液动力，其线性化方程可以表示为

(13.2)

式(13)中Fms是作用在主级阀芯上的稳态液动力，其线性化方程可以表示为

Fms=Cmym

(13.3)

式中：Cm=CvCdπDm2sin(2θ2)p1T，是作用在主级阀芯上的稳态液动力系数。

3 仿真

为了消除上述动态方程的微分项，进行了拉普拉斯变换。所推导的频率域中的传递函数可以表示为

(14)

式中：F(s)和p1(s)分别是f(t)和p1(t)的拉普拉斯变换。φ1、φ2、φ3、α、β、γ和λ是与所开发水压溢流阀参数相关的系数。水压溢流阀相关参数(均为国际标准单位)和传递函数系数如表1所示。

表1 水压溢流阀相关参数和传递函数系数

3.1 稳定性

通过建立阀的传递函数的MATLAB/Simulink模型来分析阀的动态特性。当初始参照压力是14 MPa、输入80 L/min的阶跃流量时，阀的压力响应是发散的，如图6所示，这表明阀是不稳定的。

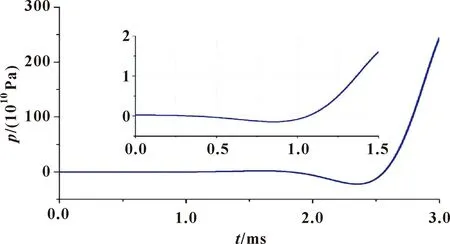
图6 所建数学模型在初始条件下的阶跃响应

作者发现表1中β为负值，根据Routh判据，这是引起阀不稳定的原因。然而在阀的可接受的参数优化调节范围内β值不能被调为正值，这显然是不合理和不可接受的。文中通过输出反馈补偿Grc(s)来克服阀的不稳定性，如下所示。

如果Grc(s)=τa+τbs，那么

(15)

式中：H*(s)代表输出反馈补偿之后的表达式p1(s)/p(s)。而H*(s)可以通过补偿一个液阻实现。

证明：

考虑到补偿的可实现性，同时Cc也是需要优化的系数。

首先，假设有液阻用于补偿在先导级A腔和P腔之间，如图5所示。从p(s)到p1(s)的传递函数可以表示为

(16)

式中：r1=t1，r2=t2，r3、t3、r4和t4是与阀的参数及补偿阀的阻尼系数Cr和阻尼系数Cc有关的系数。所以有

(17)

式中：ωa、ωb、ωc、ωd、ζb和ζd是可以用MATLAB求解的关于Cr和Cc的函数。通过同时优化Cr和Cc得到一组合适的解满足ωa<<ζbωb和ωc<<ζdωd。 这样式 (17)可以简化为

(18)

式中：ka代表二阶项的幅值。

比较H*(s)和式(18)的形式，作者发现H*(s)可以近似通过一个液阻实现。

其次，推导Cr的步骤如下：

因为H*(s)=p1(s)/p(s)，从式(15)和(18)可得：

(19)

(20)

因为ωa、ωc与Cr、Cc有如上面所提到的函数关系，则式 (20)可以表达为

(21)

方程组(21)表示输出反馈补偿可以近似通过补偿一个液阻实现。

最后，τa和τb范围的确定如下：

从上文知输出反馈补偿可以表示为

Grc(s)=τa+τbs

(22)

补偿后从F(s)到p(s)的传递函数可以表示为

(23)

τa和τb的范围可以基于Routh判据在Mathematica软件中计算出来。最终τa是在稳定性判据的基础上由稳态误差决定，τb由开环Nyquist图推断出来。

当τa=1.592 3×10-6时，τb的值是基于稳定性判据来选择的，如表2所示。τa和τb的数值范围会决定Cr和Cc的值，如式(21)所示。 恰当的Cr和Cc会被选来同时满足ωa<<ζbωb和ωc<<ζdωd，这样从p(s)到p1(s)的传递函数的简化是合理的，如式 (18)所示。这样H*(s)可以通过补偿一个液阻实现。

表2 τb的数值

补偿的实现可以通过使用液阻来完成，但不能通过调节C1来实现。补偿不仅使用了一个液阻，而且隐含了一个由于先导阀芯运动而产生的动态容腔。由于p的微分项包含在输出反馈补偿中，所以补偿可以认为是动压反馈补偿。

基于以上分析，可知补偿阻尼使得阀成为一个压力反馈控制阀。

3.2 响应

当阀在初始点xp0并且初始边界压力是14 MPa、阶跃流量为80 L/min时，补偿之后的闭环Bode图如图7所示。Bode图中，输出和输入分别是压力和相关调节力。

图7 补偿之后阀的传递函数Bode图

由于τb在决定频响的动态特性方面扮演着重要的作用，同时对阻尼比ζ和超调也有影响，如图7所示。补偿之前阀是不稳定的，而补偿之后阀变稳定。从中可知补偿可以解决上面提到的问题，并且补偿之后的阀有较大的频响。

4 阀的压力响应实验

实验台的原理如图8所示，水压源选的是九柱塞的柱塞泵。泵的额定压力和排量分别为16 MPa和80 mL/r。常开两通开关阀用来控制测试阀的阶跃流量输入。

图8 实验台原理

补偿阀在不同阶跃流量下的压力响应如图9所示。除少数压力超调接近1%～20%，大部分压力大于6 MPa、流量大于60 L/min的响应误差小于1%，压力波动小于5%。

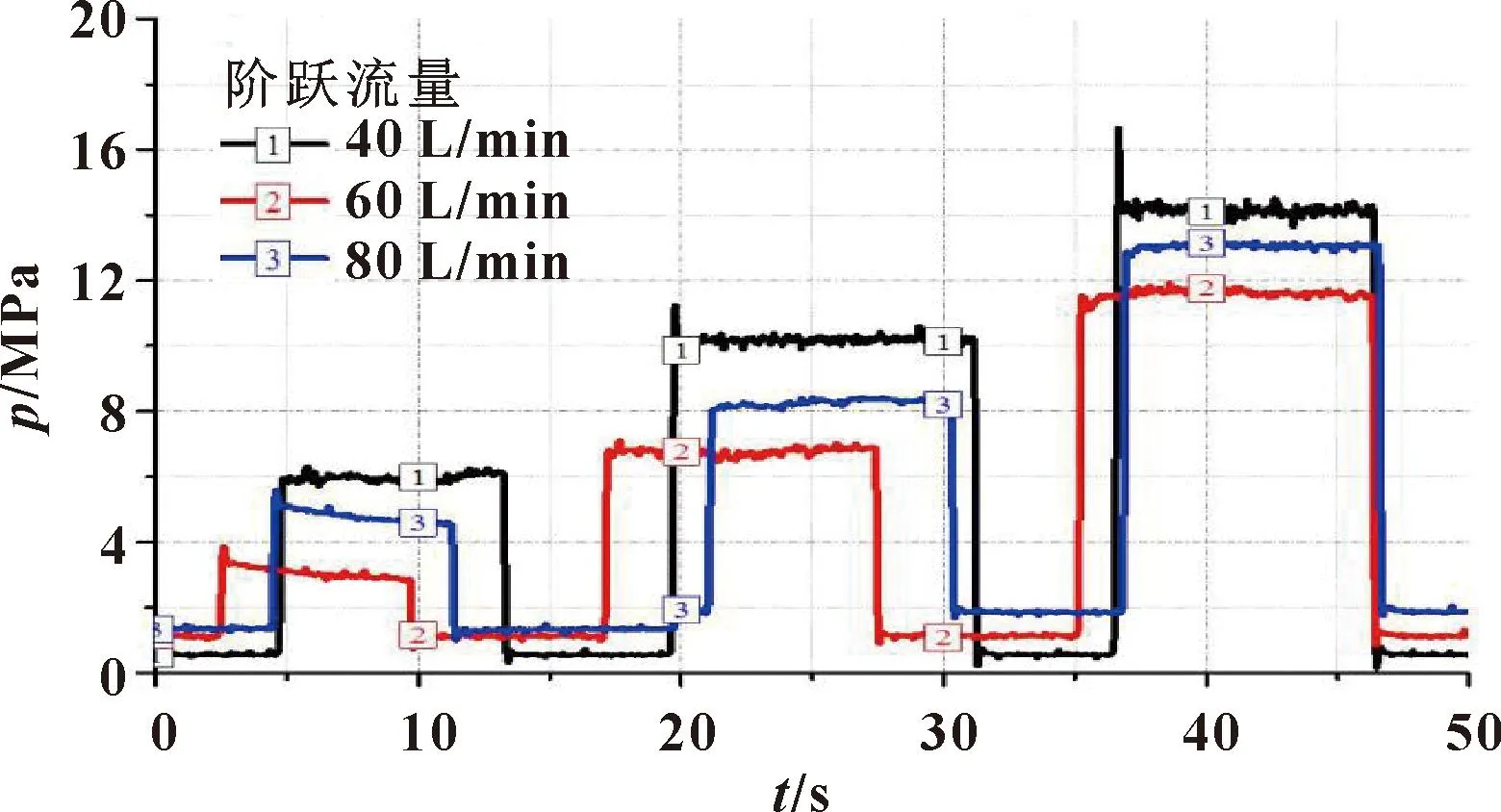
图9 被试阀在不同阶跃流量下的压力响应

5 结论

设计一种先导级环形间隙阻尼作为先导液阻的水压溢流阀。环形间隙阻尼的设计达成两个目标：形成对应的先导阻尼和形成环形流动润滑层来避免先导级阀芯与阀套之间的摩擦。

建立了水压溢流阀的数学模型来分析阀的动态特性。通过仿真和分析知阀是不稳定的。为了使阀获得稳定的输出，做了输出压力反馈补偿，这是一种动压反馈补偿。 所开发的先导级含有环形间隙阻尼液阻的水压溢流阀通过补偿可以获得稳定，参数获得了优化。大部分压力大于6 MPa、流量大于60 L/min的响应误差小于1%，压力波动小于5%。