基于刚柔耦合的提升机钢丝绳横向振动因素分析

韩壮禄，龙盛蓉，陈学宽，宋奕霖，李志农

(1.南昌航空大学江西省图像处理与模式识别重点实验室，江西南昌 330063；2.南昌航空大学无损检测教育部重点实验室，江西南昌 330063)

0 前言

摩擦式提升机在承载容器提升和下放的运行工况下，由于钢丝绳具有柔性结构特征，其在运行过程中会出现滞后、惯性运动及振动等情况。由于较大负载的存在，钢丝绳在运转时会产生长度的改变，从而使振动更加严重。特别是钢丝绳制动时的横向振动，过大会导致剽绳、跳绳等情况，若振幅大于相邻钢绳之间的距离的1/2，则会使钢丝绳相互缠绕。在紧急停止运行的情况下，其横向振动加剧，可能导致钢丝绳与摩擦轮接触的地方偏移，即发生打滑现象，还可能导致钢丝绳断裂。因此，根据动力学原理对提升机系统进行建模并分析其在制动阶段不同加速度与不同制动曲线下横向振动特性很有必要[1]。

刘义等人[2]研究柔性体钢丝绳模型建立方法，使用RecurDyn和ANSYS软件对JK-2/20型钢丝绳张力进行了仿真研究。KIMURA等[3]利用SDOF研究动态响应，建立了提升电梯的横向振动模型。梁敏[4]深入研究立井提升系统的钢丝绳动态特性，揭示了钢丝绳的不同结构参数对矿井提升钢丝绳横向振动的影响。YAO等[5]研究了运动性能良好的摩擦式提升机钢丝绳的横向振动特性。包继虎等[6]提出了用于变长度提升系统钢丝绳横向振动模型，通过改变外界激励来分析钢丝绳的变形情况。寇保福等[7]以Kelvin黏弹性模型为基础，等效平衡钢丝绳的质量于罐笼上，采用Hamliton方程推导出柔性提升系统钢丝绳横向振动的偏微分振动方程。吴娟等人[8]采用连续弹性体方法推导摩擦提升钢丝绳横向振动方程。KACZMARCZYK、OSTACHOWICZ[9-10]研究了缠绕提升系统的动力学，提出了钢丝绳三维振动模型，并研究了重载深井的特性。文献[11]基于Hamliton原理推导可变长度提升系统运动状态下钢丝绳微分方程。彭霞等人[12]将钢丝绳看作连续的弹性体，在边界激励下建立并求解悬绳横向振动方程。吴虎城等[13]基于Hamilton原理推导了钢丝绳提升系统横向振动方程。黄家海等[14]建立基于分布参数的落地式摩擦提升机动力学仿真模型，并通过实验验证仿真模型有效性。PENG等[15]采用Galerkin方法研究多层缠绕卷筒布置形式对钢丝绳振动特性的影响。MARIAN[16]利用集中参数离散方法，建立简化的提升系统数学模型，并计算了钢丝绳工作时的动张力。

上述内容主要在提升机系统数学建模方法以及不同角度分析提升机动力学特征做研究，未反映出钢丝绳的柔性特征以及摩擦轮与钢丝绳之间的刚柔耦合接触问题。本文作者在上述基础上以多体动力学仿真软件为载体，充分考虑钢丝绳的柔性特性，还原钢丝绳与摩擦轮之间的接触特性，建立刚柔耦合的摩擦式提升机仿真模型。并在此模型基础上研究提升系统动力学特征与制动曲线对动力学特征的影响，并开展试验验证。

1 提升机钢丝绳实验分析

以某矿副立井摩擦提升系统为实验对象，在摩擦轮下方4 m处，4根钢丝绳在同水平下布置4个单向传感器，测试提升机钢丝绳横向振动，传感器测试数据经INV3060S数据采集仪采集后，将该数据进行积分变换后得到速度变化及振幅变化曲线，如图1所示。

图1 测试装置(a)与测试原理示意(b)

测试采用图2所示的运行速度，图3为运行加速度。0～10 s，系统处于停机状态；在10 s时刻，制动系统立即松闸，驱动电机开始启动；速度在 10～20 s由0逐渐增大到1 m/s；20～30 s阶段，系统以1 m/s速度匀速运行；30～40 s 阶段，速度由1 m/s增加到4 m/s；在40～60 s阶段，以4 m/s匀速运行；60～66 s为减速阶段，此时驱动电机开始减速，速度由4 m/s逐渐减小到0.5 m/s；66～75 s为低速爬行阶段；75 s时，制动系统抱闸，加速度瞬间达到最大值，驱动电机输出速度降为0，提升机缓慢停车。

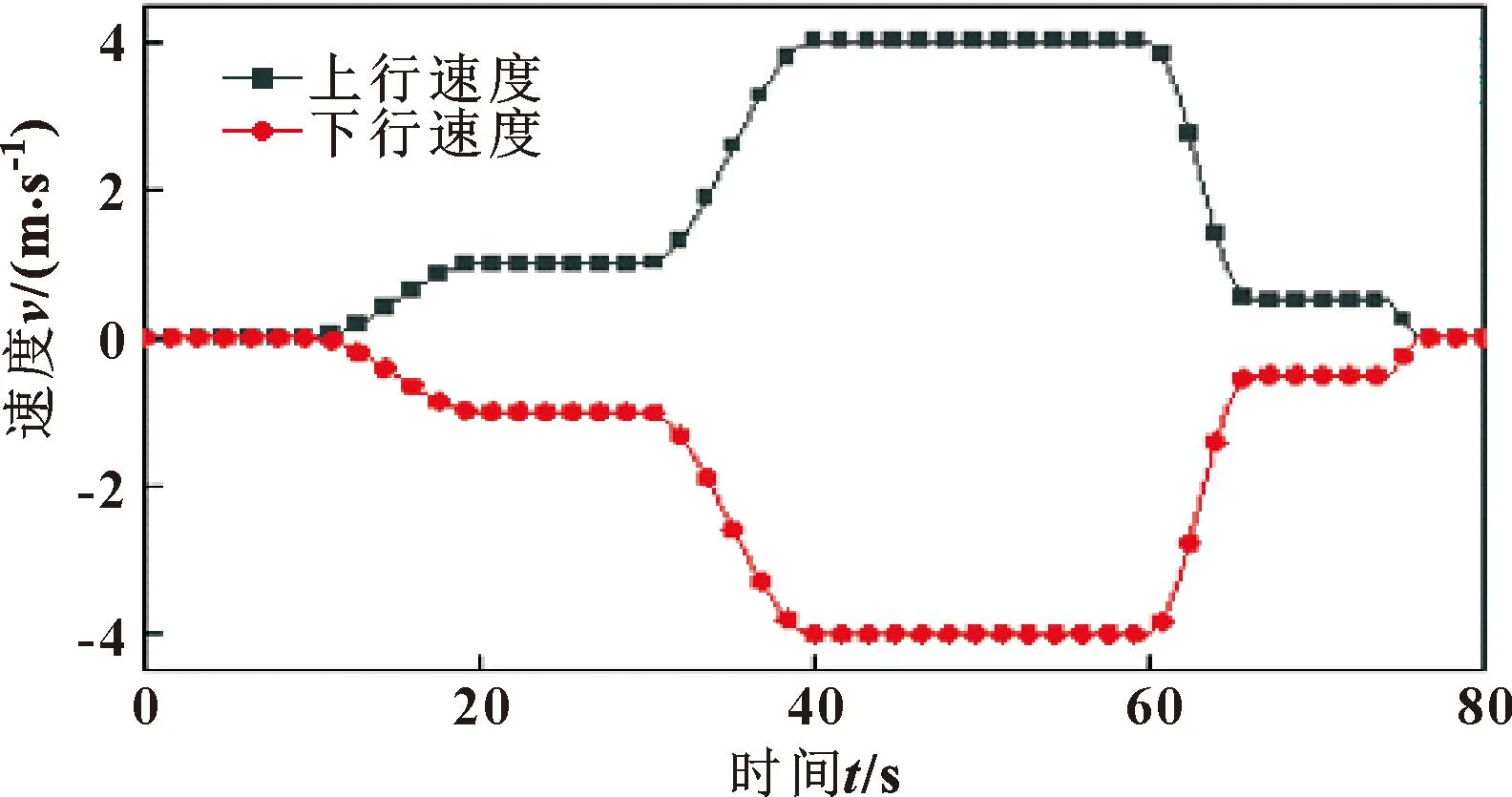
图2 主轴运行速度

图3 主轴运行加速度

2 提升机钢丝绳数值仿真研究

目前提升机钢丝绳仿真研究主要采用数值模拟方法，该仿真过程中未考虑提升机运行过程中钢丝绳与摩擦轮之间的柔性接触。本文作者采用有限元法多柔性体技术，充分考虑系统运动情况下的动力学特征，将有限元分析与多体动力学分析相结合，避免了由于模态缩减出现的弊端。模型采用完全递归算法和基于相对坐标系运动方程建模，将钢丝绳柔性化，还原钢丝绳与摩擦轮之间的摩擦力，建立如图4所示的提升机数值仿真模型。其中，钢丝绳与仿真系统中的各部分如摩擦轮等的接触类型设置为柔性线-面接触；给主轴添加驱动速度，该速度由step函数驱动而成。

图4 落地式摩擦提升机动力学仿真模型

3 钢丝绳的振动特性测试与模型验证

文中将提升机系统施加的运动过程分为加速、匀速、主加速、匀速、主减速、制动6个过程，下面以step驱动函数对比分析钢丝绳在运动过程中的振动特性。

图5为空载上行、下放工况下钢丝绳横向振动仿真与测试对比曲线。在0～10 s的时间内，系统处于停机状态，试验信号全部是噪声造成的，幅度较小；10～20 s为初加速，速度逐渐提高至1 m/s，横向振幅较停机状态时稍有增大；在20～30 s的加速期，速度从1 m/s上升到4 m/s，随着运行速度的增大，振动信号有一定的提高，但幅度较小；在40～60 s主匀速运转阶段，提升机的转速为6 m/s，振动信号比较稳定，这是在高速运转中，刚性罐道变形或本身缺陷对钢丝绳的外部激励而引起的振动分量；60～80 s，下行阶段，钢丝绳振动幅度更小，振动频率增加很快，振动剧烈。上行运行和下行运动的钢丝绳横向振动不同。上行时钢丝绳缩短造成的振动能量很大，易造成提升系统失稳现象，这也是上行容易发生事故的原因。

图5 仿真与测试结果对比

从图6所示的钢丝绳振动的测试值FFT曲线可知，横向振动主要发生在低频区，所测的频率主要在4 Hz以下。这是由于钢丝绳具有多个自由度，振动通常表现为多自由度振动，因此其振幅频率特征与多个峰值对应。

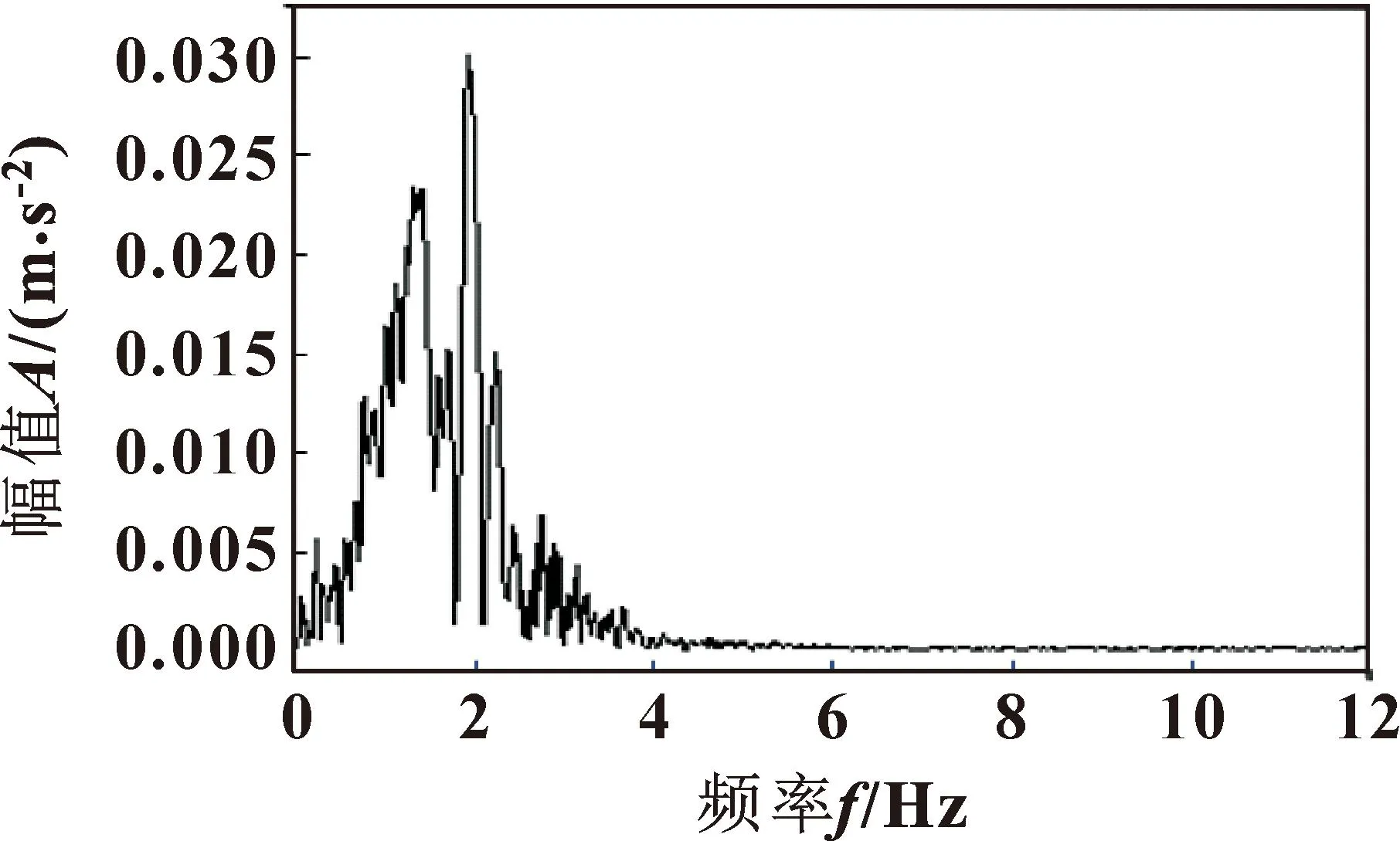
图6 横向振动FFT变换

4 摩擦提升机制动阶段横向振动分析

4.1 加速度对提升系统制动阶段振动的影响

在制动阶段，制动器加速度会影响提升机钢丝绳的振动特性。设置运行速度为6 m/s，分别仿真下放工况制动加速度a1=0.30 m/s2、a2=0.45 m/s2、a3=0.60 m/s2时的钢丝绳横向振动加速度。提升机速度在6 m/s时，开始准备减速，在制动阶段先产生5 s的预备阶段，开始减速到提升机速度为0，结果如图7所示。

由于加速度增大，振动逐渐加剧。由于钢丝绳是柔性部件，在10 s时，加速度开始变化时，并没有明显变化。这是主轴产生的制动力矩并不能即时传递到钢丝绳，这种现象造成了振动加速度的延迟变化。从图8可以看出：随着加速度逐渐增大，钢丝绳横向振动也逐渐增大，这会对钢丝绳以及摩擦轮的寿命产生影响。但在实际工况中，为了保证生产效率，也要在提升效率和减小振动中寻求平衡。

4.2 制动曲线对提升系统制动阶段振动的影响

提升机运行过程中，制动阶段的振动极易引起摩擦轮与钢丝绳之间、主轴与摩擦轮之间的碰撞。通过对制动时间一定条件下、不同制动曲线的研究，进一步探索提升系统更好的制动速度。仿真时提升系统为空载运行，制动产生最大运行速度v=6 m/s，重载下放高度为300 m，制动时间为20 s，分别以图9所示曲线作为输入进行仿真。通过仿真可以得到钢丝绳某点制动时刻的横向加速度。选取制动过程中常用的矩形、梯形及正弦制动曲线进行研究，其表达式分别为式(1)—(3)。

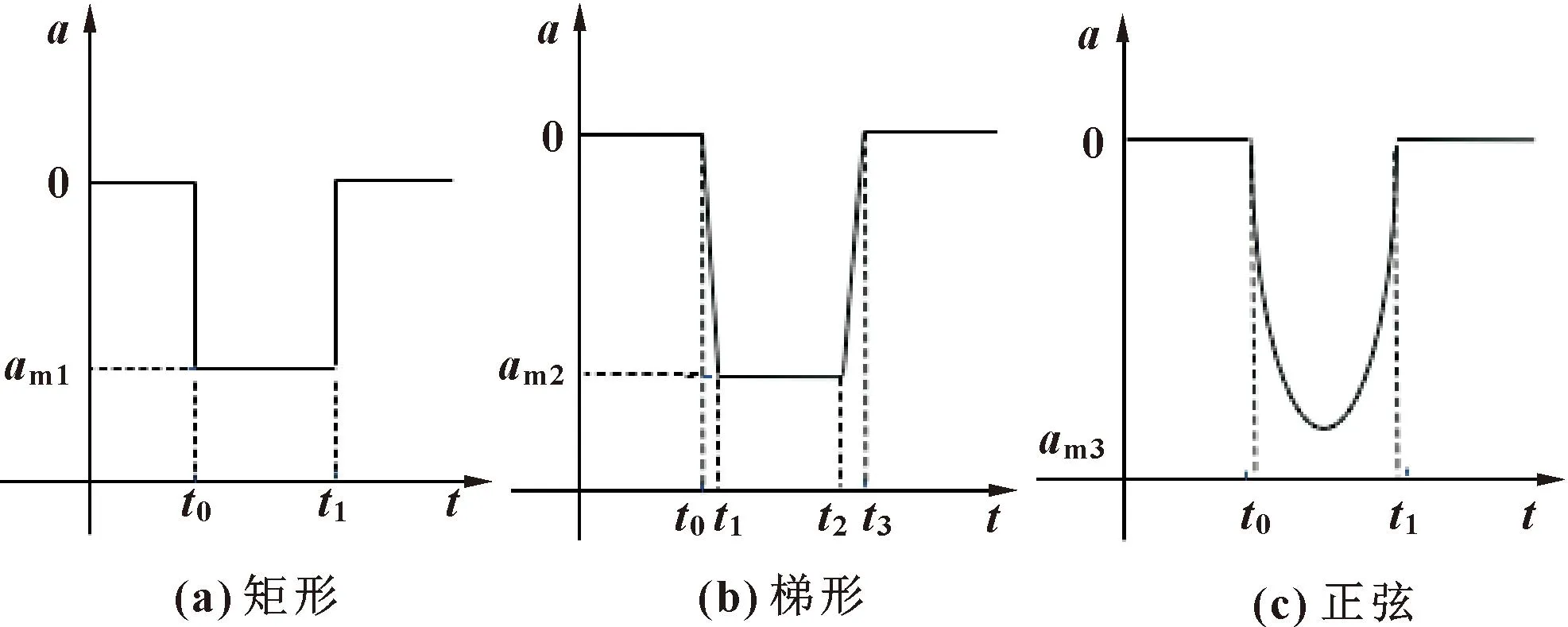
图9 不同制动曲线加速度

矩形曲线表达式为

(1)

梯形曲线计算式为

(2)

正弦曲线计算式为

(3)

对比上述曲线，在相同制动时间与相同制动距离下，矩形的制动加速度最小，梯形曲线制动加速度略大于矩形曲线制动加速度，而正弦曲线的制动加速度远远大于其他两个制动加速度。

图10、11为上行、下行运动时不同制动曲线下钢丝绳横向加速度变化曲线。对比图10中的仿真曲线振动幅度依次减小；在第5 s时，提升机的加速度开始变化，由图10可知，3种运行状况均在5 s时振动加速度有不同程度的变化。在制动阶段，梯形和矩形的制动曲线所产生的加速曲线的起伏幅度有所降低，而在正弦曲线处，则有明显的加速变化。

图10 上行运动不同曲线钢丝绳加速度

图11 下行运动不同曲线钢丝绳加速度

分析可知，当制动时间一定时，am1

在初速度、载荷等参数相同时，若要在规定时间内实现快速停车的目的，对比3组数据(表1)，在相同制动时间内，矩形制动加速度最小，制动冲击也最小；梯形制动加速度最大值略大于矩形制动加速度最大值，制动冲击在减速中期产生较大浮动；采用正弦制动曲线时，提升系统会产生打滑，且在中期制动冲击持续时间更久。

表1 不同制动曲线钢丝绳振动特征值

从表1可以看出：基于矩形曲线的特征值最小，正弦曲线下的振动的均方根值、峰峰值都大于矩形曲线。不同制动曲线下的均方值分别为0.027 9、0.031 8、0.014 5 m/s2。设矩形曲线下均方根值为单位1，而正弦曲线均方根值增加了92%，梯形曲线均方根值增加了119%。从各不同制动曲线来看，矩形曲线的峰峰值最小，振动幅度最小。这表示在制动时间一定时，采用矩形曲线制动效果更好，因此采用矩形曲线可以降低提升机制动时产生的横向振动。

5 结论

(1)构建了基于刚柔耦合的提升机系统模型，并通过现场测试验证模型的准确性。测试曲线能够很好地反映提升机工作中的典型横向振动特性，为进一步研究提升机的制动曲线提供了依据。

(2)由于制动阶段属于高发危险阶段，会引起强烈的碰撞及冲击，会对提升系统的寿命造成影响，甚至会对安全人员造成隐患，故在上述模型的基础上对提升机系统的制动阶段进行研究。研究结果表明：上行运动的横向振动幅值明显大于下行曲线，在实际生产中，上行运动产生能量更大，更易引发安全事故。在制动时间一定时，矩形曲线的振动加速度最小，正弦曲线的加速度最大。矩形曲线的特征值均小于其他制动曲线。

(3)制动阶段的加速度变化会影响到提升机横向振动。研究结果表明：在仿真中，加速度传导的振动特征会有延迟效果且加速度增大，钢丝绳横向振动会变大。