单自由度振动台随机波形复现控制策略研究
2023-12-20张兵杜厚羿朱方正吴一凡饶俊森邱龙涛
张兵,杜厚羿,朱方正,吴一凡,饶俊森,邱龙涛
(1.江苏大学机械工程学院,江苏镇江 212013;2.镇江市流体传动与控制重点实验室,江苏镇江 212013;3.丹佛斯动力系统(江苏)有限公司,江苏镇江 212013)
0 前言
振动环境模拟广泛应用于航空航天、汽车的抗震测试[1]、土木桥梁建筑[2]等各领域。液压技术由于其传动力量大,易于传递及配置,在很多关键技术领域被当作核心的基础实验来复现真实的振动环境情景。例如:工程材料中的高频率疲劳测试试验,汽车等运输机械的路面波振动环境模拟试验[3],桥梁、堤坝等大型建筑物的防震测试等[4-5]。
振动控制的作用是对伺服控制的控制信号进行迭代补偿,基于迭代学习的振动控制技术是振动台控制中最常见的补偿策略。GAVAGHAN、BOND[6]提出了傅里叶转换的交流伏安法,减弱振动试验中高频谐振噪声的干扰。MROZ等[7]提出了应用离散传递函数分析法补偿电液伺服阀控制的非线性,提高响应波形的跟踪精度。TORVIK[8]对液压振动台系统中的阻尼比进行研究,根据阻尼比系数进行振动试验,提高扫频控制的精度。张连朋[9]提出用均匀随机信号激励系统进行系统辨识,然后用补偿后的驱动信号激励系统,可以解决相位滞后和幅值衰减的问题。CORNELIS等[10]通过加权修正系数和改良激励信号两方面来改进离线迭代控制。MOTEN等[11]将离线迭代控制和自适应逆控制相结合进行振动台时域波形复现,提高了迭代效率。
由于电液伺服系统中存在伺服阀非线性流量-压力特性、流体体积压缩特性和液压油温度、液压缸上的摩擦力等因素的影响,使得振动台系统中实际存在着响应信号滞后于参考信号的时间,因此需要在迭代学习控制的基础上对控制算法进行完善。
本文作者采用对单轴电液伺服振动台伺服控制系统建模分析、振动台波形复现迭代控制算法研究、试验验证相结合的方法,对液压振动台随机波形复现控制策略进行研究。在证实迭代算法的有效性后可将其用于多自由度振动台、振动台组进行随机波形复现控制策略研究。
1 振动台三状态控制器设计
试验台采用非对称液压缸,图1为对称阀控制非对称缸原理,其中:q1、q2分别为流入液压缸无杆腔和有杆腔流量;ps为油源压力;p0为回油压力;A1、A2分别为液压缸无杆腔和有杆腔的有效面积;p1、p2分别为液压缸无杆腔和有杆腔压力(Pa);FL为折算到活塞杆的等效干扰力;mL为负载惯性折算到活塞处的等效质量;xv为阀芯位移;y为负载位移。
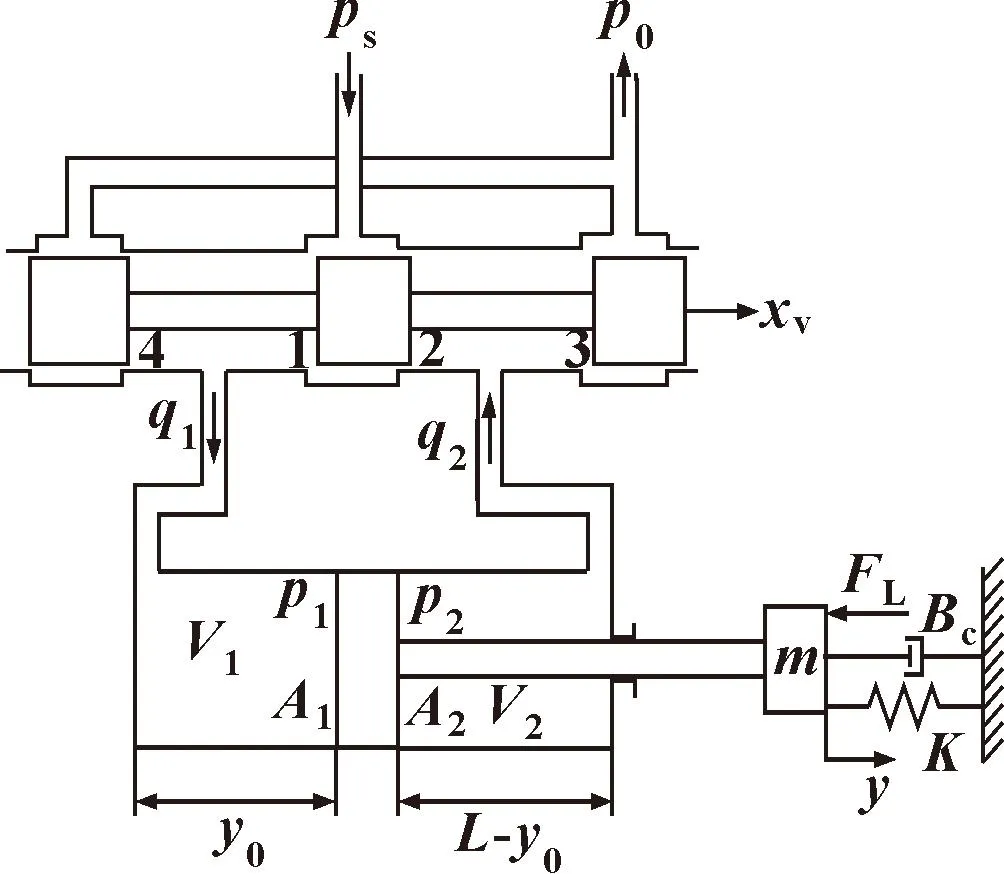
图1 阀控非对称缸结构简图
假设:(1)回油压力为0,即p0=0;(2)忽略液压缸的漏损。
在振动台伺服系统控制策略研究中,使用三状态控制器[12]来拓展系统的频带宽度,如图2所示。三状态反馈可以提高系统的阻尼比,三状态前馈能提高系统的稳定性,改进系统的跟踪精度,提高系统的频宽。
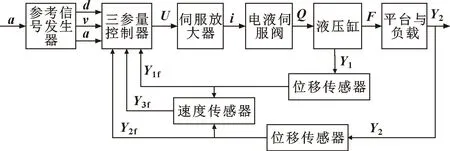
图2 液压振动台伺服系统原理框图
1.1 三状态反馈
三状态反馈控制应用极点配置方法配置系统极点,其原理如图3所示。三状态反馈控制系统的闭环传递函数为
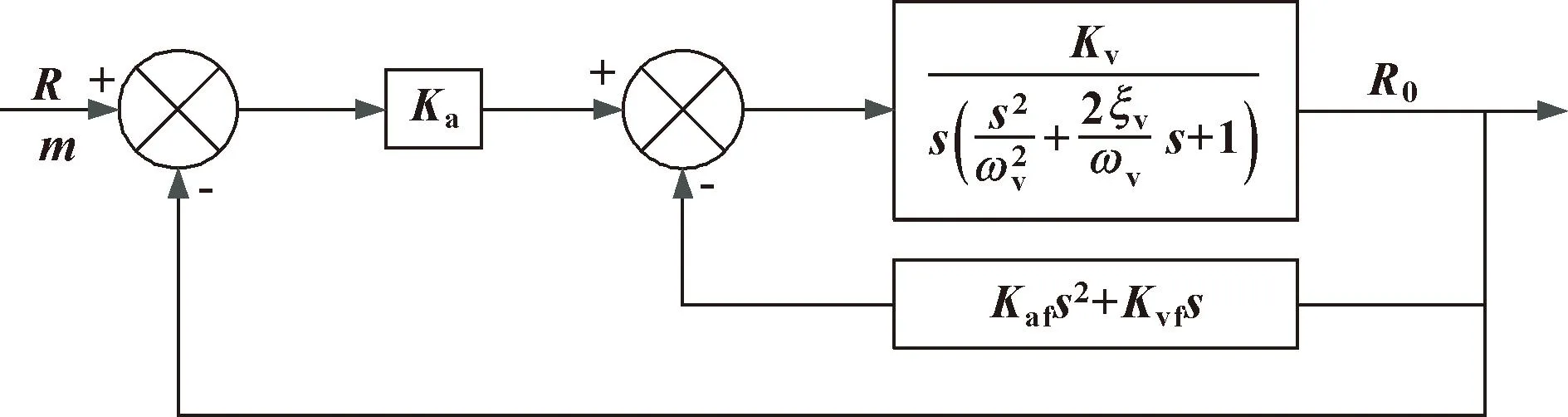
图3 三状态反馈控制系统框图
(1)
式中:ωr为期望系统最终频宽对应的频率;ωnc一般为1.05~1.20倍的液压固有频率;ξnc一般取0.7。
由系统框图建立的电液伺服控制系统数学模型,得到简化后的系统开环传递函数为
(2)
式中:kk为系统开环增益;ωk为系统固有频率;ξk为阻尼比。系统在经过三状态反馈后会与期望的传递函数特征方程相同,令Kv=KaKq/A1,可得:
(3)
式中:Kdf为位移反馈;Kvf为速度反馈。
1.2 三状态前馈
为了使系统的带宽得到进一步扩展,通常是在三状态反馈调节后的系统中串入二阶微分环节B(s)[13-14]。三状态前馈的原理如图4所示。
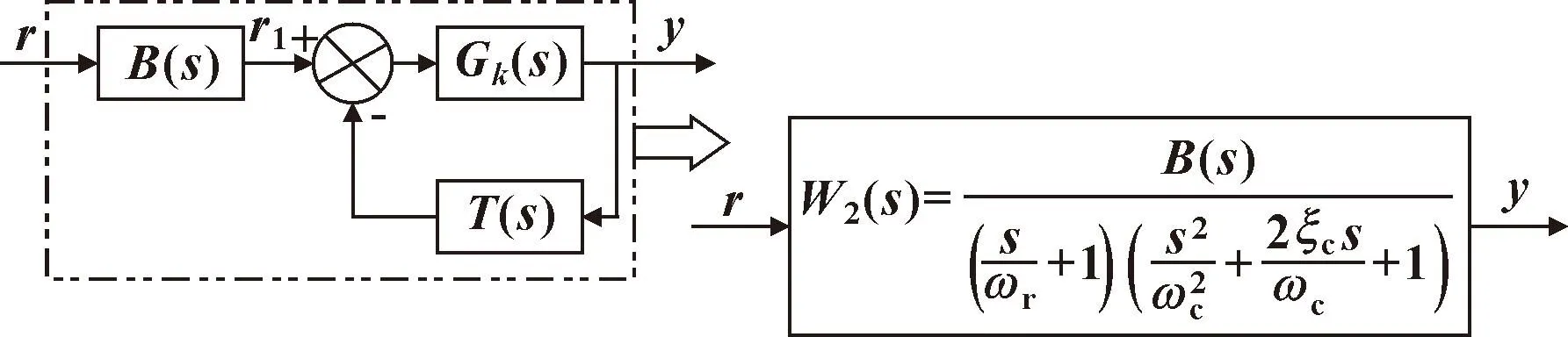
图4 三状态控制原理
设B(s)为二阶微分环节,则:
(4)
式中:Kdr为位移前馈系数;Kvr为速度前馈系数;Kar为加速度前馈系数。
为保证系统增益不变,取Kdr=Kdf,有:
(5)
由图5可见:在引入三状态控制后,系统的频宽扩展到40 Hz左右。阶跃响应如图6所示。
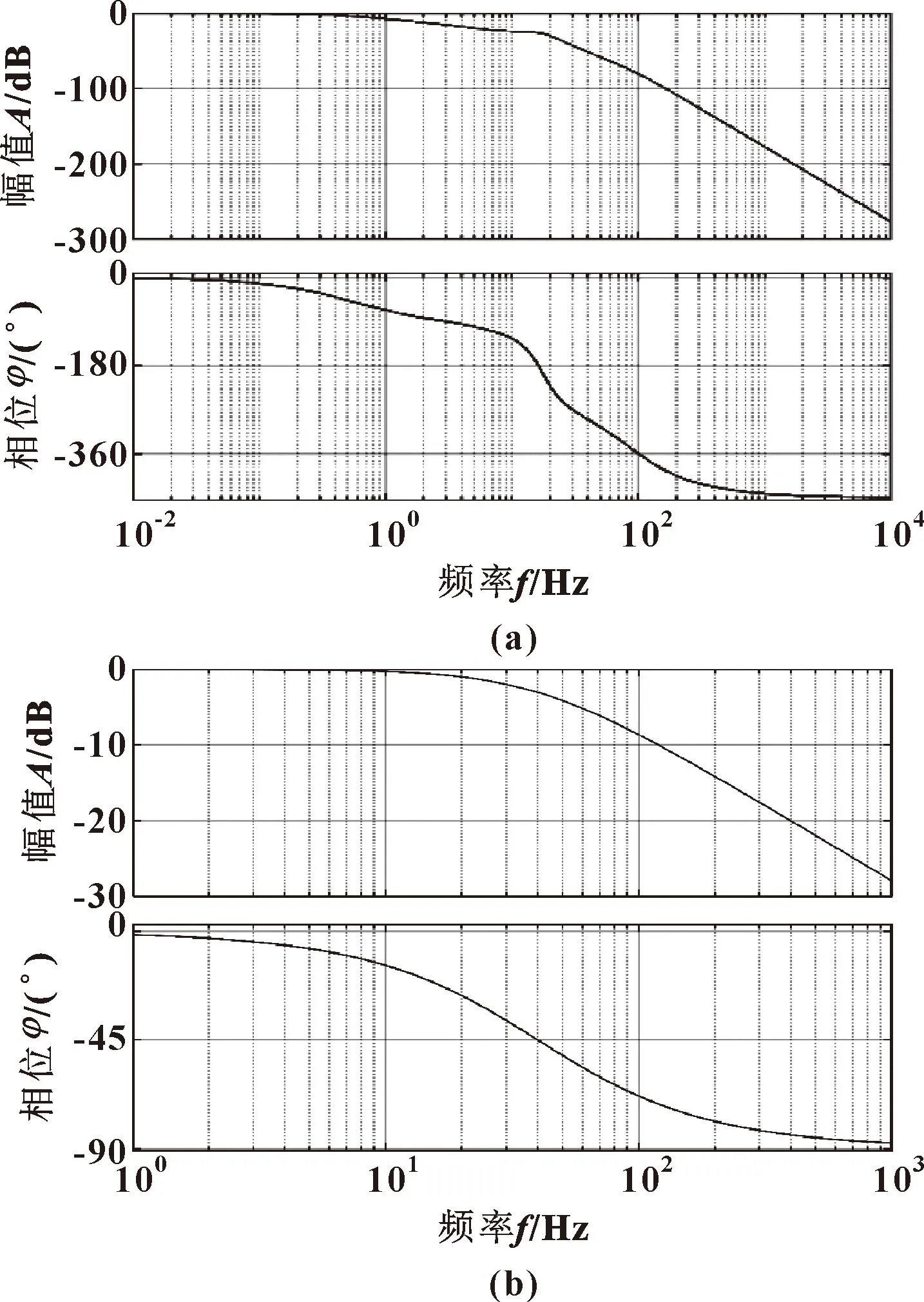
图5 加入三状态控制前(a)、后(b)系统频率特性

图6 加入三状态控制前(a)、后(b)系统单位阶跃响应
由图6可知:系统在使用三状态控制策略后响应时间达到0.027 s,比未加入三状态控制时更迅速。
2 基于时滞估计的迭代学习控制算法
振动台波形复现的原理[13]如图7所示。

图7 振动台波形复现原理
进行波形复现试验前已知的条件只有时域参考信号,要想获得振动的时域驱动信号就必须对振动台系统进行系统辨识得到系统的频响函数H(f),然后对H(f)求逆得系统阻抗函数Z(f),根据期望信号和阻抗函数求出驱动信号。
2.1 系统辨识算法
在进行随机加速度波形迭代控制试验之前,使用随机信号对振动台系统进行激励[15]。根据系统的输入和输出辨识出系统的频响函数[16]。波形复现需要先高精度地辨识出系统的频响函数。图8为系统的输入输出模型,u(t)为系统真实的输入信号,v(t)是系统真实的输出信号。

图8 输入输出系统模型
试验采用H1辨识法。H1估计法的频响函数为
H1(f)=Gxy(f)/Gxx(f)
(6)
式中:H1(f)为H1法频响函数估计;Gxx(f)为输入信号自功率谱密度;Gxy(f)为输入和输出信号的互功率谱密度。
2.2 迭代学习控制原理
在实际的电液伺服控制中,响应的加速度信号滞后于驱动信号,因此使用基于时滞估计的电液伺服振动台迭代学习控制算法。其中,真实的电液伺服振动台系统传递函数用Ga(z)表示,τ用来表示滞后采样周期,可得下式:
Ga(z)=Ha(z)z-τ
(7)
(8)
uj表示第j次迭代系统的输入信号,ra(k)表示振动台的加速度参考信号,βj表示第j次迭代增益。
推导得第j次迭代的跟踪偏差为
ΔHa)]ej-1(k)
(9)
由式(9)可得到:
(10)
振动台迭代学习控制算法的收敛条件为
(11)
由式(11)可知:迭代学习控制的稳定性以及收敛速度是由迭代增益βj和模型估计的偏差以及系统的不确定度ΔHa决定的。
2.3 滞后时间估计
若系统不存在滞后的情况下则可以直接计算出系统响应加速度波形与系统控制波形之间的相关系数,来衡量两者之间的相似程度。当系统响应信号存在时间滞后时,可分步将响应波形向左平移减小时滞效应,提高相关系数。在相关系数达到最大值时,便得出系统的滞后时间即向左平移了多少个采样周期即是控制系统滞后时间。基于上述思想,系统时滞估计步骤为:
(1)将振动台的响应信号y(k)(k=1,2,…,N)整体向左平移1个采样周期T,第i次平移后的波形为
(12)
(2)计算yi(k)与参考波形u(k)(k=1,2,…,N)的相关系数;
(3)当i≥2时,当计算的相关系数比前一次小即停止循环,系统的滞后时间为τ=(i-1)T。
2.4 基于时滞估计的迭代学习控制算法流程
在考虑系统的时滞问题后,电液伺服振动台迭代学习控制的流程如图9所示。

图9 基于时滞估计的振动台迭代学习控制流程
其流程如下:
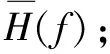
(2)计算初始驱动信号。根据式U(f)=R0(f)/H(f)计算出U(f),对U(f)做IFFT变换得到时域初始驱动信号[u(t)]0;
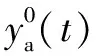
(13)
式中:N为总采样点数;Ts为采样周期。
(5)计算响应信号与参考信号的差,按式(14)所示用时域参考信号减去时域响应信号得[e(t)]0,对偏差信号[e(t)]0做快速傅里叶变换得到[e(f)]0;
(14)
(6)输入信号修正项的求取。将上一步求得的时域偏差信号[e(t)]0进行快速傅里叶变换得频域信号[E(f)]0,再由式(15)计算出[ΔU(f)]0,对[ΔU(f)]0做IFFT变换得到时域修正信号[Δu(t)]0;
(15)
(7)改良系统控制输入信号。根据上一步得到修正项[Δu(t)]0得到下一次迭代时系统的控制输入信号[u(t)]1;
[u(t)]1=[u(t)]0+β1[Δu(t)]0
(16)
(8)循环步骤(3)—(7),直至波形复现结果满足实际的需求。
3 随机波形复现实验
实验部分采用的实验平台是课题组自行组建的单自由度电液伺服振动台。图10所示为振动台系统实物,主要包括油源、振动台、冷却器、控制柜、上位机和信号调理箱等。

图10 振动台组成实物
3.1 系统滞后时间估计
对电液伺服振动台的三状态参数进行调整后,设定激励加速度信号幅值为1g,频带分别为4~20 Hz、4~35 Hz,时间为5 s的随机波复现实验,得到的台面实际响应加速度波形和期望加速度波形分别如图11和图12所示。图12中方框所标的细节图如图13所示。

图11 4~20 Hz随机波形复现结果
从图11—13能够明显地观察到:反馈的加速度波形与期望的加速度波形之间存在着滞后关系,需要先对控制系统存在的滞后时间进行估计。根据基于相关系数的纯滞后时间估计方法,将两组实验采集到的加速度输出信号循环向左平移τ个采样周期,计算输入和输出波形的相关系数如表1、2所示。
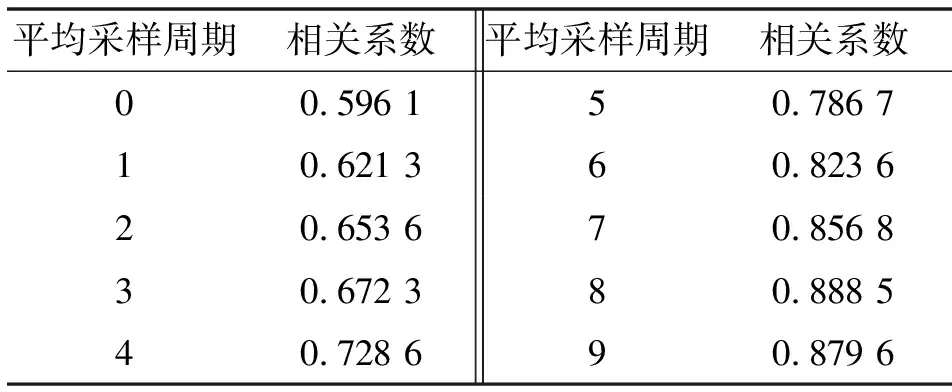
表2 滞后时间估计(4~35 Hz)
由表1、2可以看出:在进行第一组4~20 Hz随机波形复现实验时,系统滞后时间为9个采样周期;进行第二组4~35 Hz随机波复现实验时系统滞后时间为8个采样周期。将图11、12中的响应波形分别向左平移相应的滞后时间得图14、15。

图14 4~20 Hz随机波试验台面响应加速度波形(未迭代)
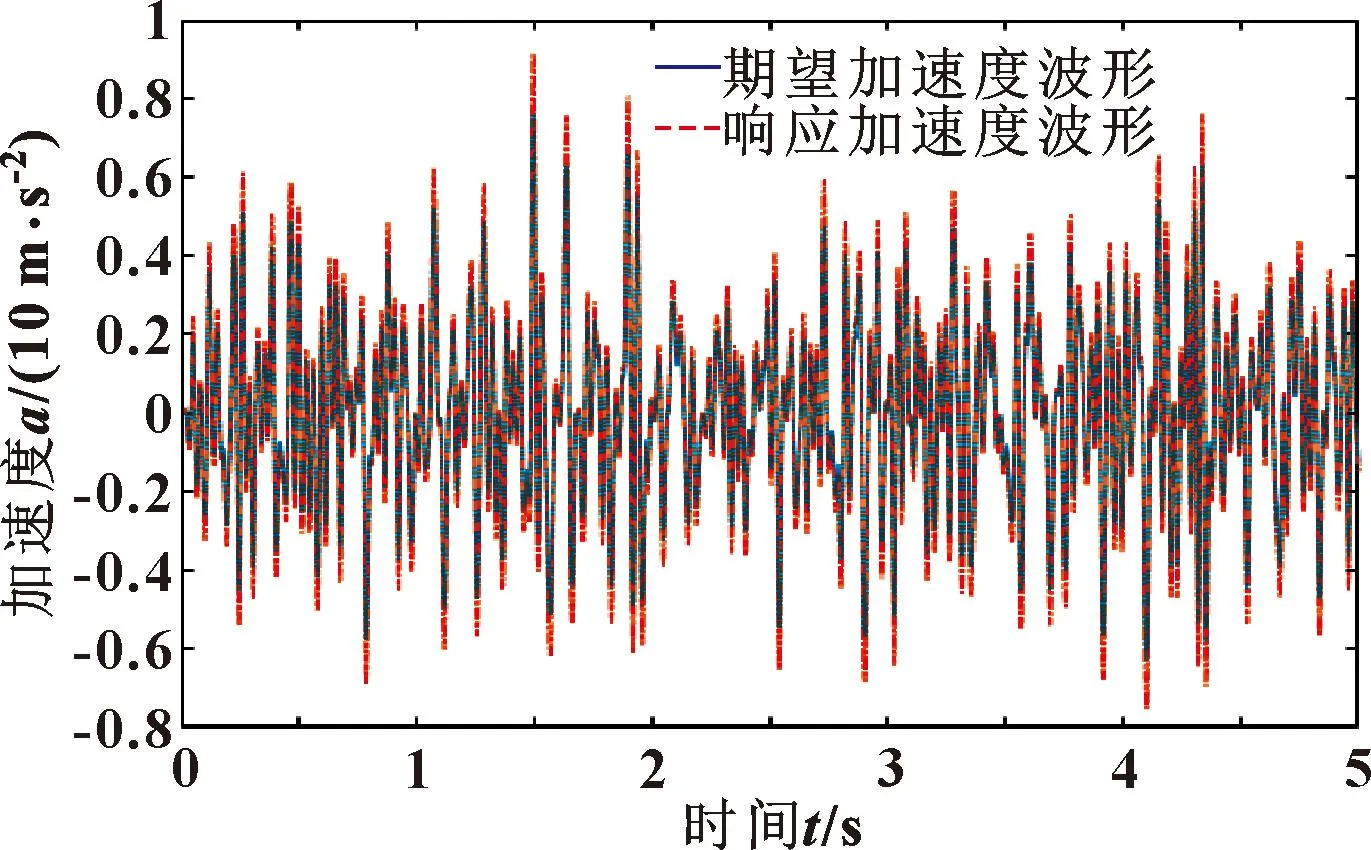
图15 4~35 Hz随机波试验台面响应加速度波形(未迭代)
3.2 目标加速度信号迭代试验结果
实验结果如图14—17所示。图14、15为频带4~20 Hz、4~35 Hz的随机波未迭代时响应加速度波形与期望加速度波形的对比。图16为频带4~20 Hz的随机波经过4次迭代后响应波形与参考波形对比;图17为4~35 Hz的随机波经过3次迭代后响应波形与参考波形对比。
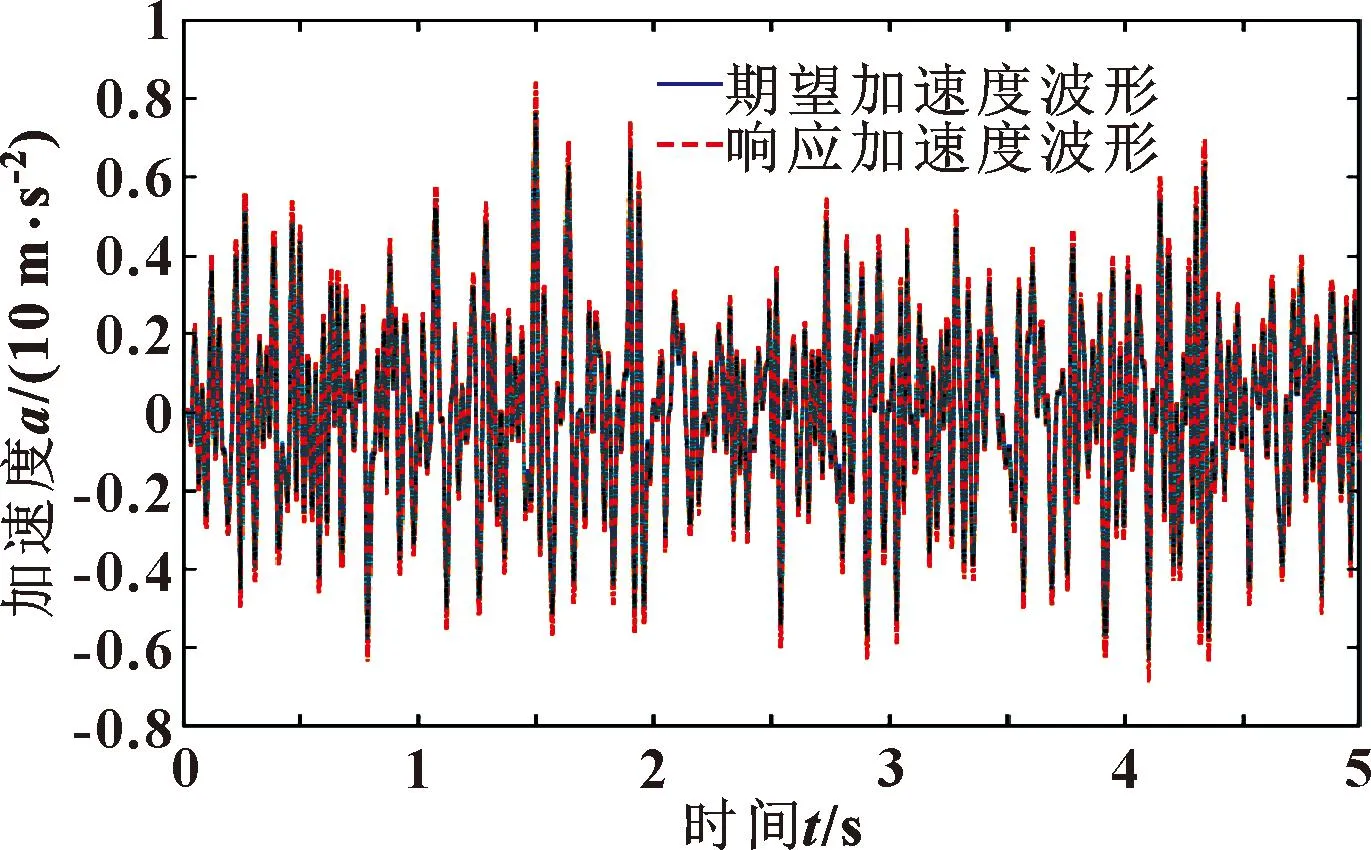
图17 4~35 Hz随机波试验台面响应加速度波形(迭代3次后)
频带4~20 Hz随机波在进行4次迭代后参考信号与响应信号的相关系数由0.886 8提高到0.921 4,频带4~35 Hz随机波经过3次迭代后参考信号与响应信号的相关系数由0.888 5提高到0.912 6。迭代后的相关系数均有所提高,证明了所用迭代控制算法的有效性。
4 总结
(1)分析了液压振动台伺服控制系统在加入三状态控制前后的系统频宽,验证了三状态控制器可以拓展系统的频宽,使振动台满足随机加速度波形复现实验。
(2)对振动台伺服系统进行系统辨识后,对滞后时间进行估计,设计了基于时滞估计的振动台迭代学习控制流程。
(3)使用单自由度振动台进行波形复现实验,迭代后的相关系数均高于迭代前的相关系数,证明了基于时滞估计迭代算法的有效性。
