基于环境吸引域的冗余机器人运动控制与实时位型优化
2023-12-20吕晓静徐智浩徐恩华
吕晓静,徐智浩,徐恩华
(1.广州民航职业技术学院飞机维修工程学院,广东广州 510403;2.广东省科学院智能制造研究所,广东省现代控制技术重点实验室,广东广州 510070;3.广州民航职业技术学院民航经营管理学院,广东广州 510403)
0 前言
随着智能制造国家战略的纵深发展,以多品种、多型号为导向的智能柔性制造成为机器人化制造的一种重要趋势。人机协作融合了人类的操作智慧和机器人的操作稳定性,是实现智能柔性生产的重要途径。
在人机协作模式下,机器人与人类的作业空间更加紧凑,导致机器人与人类作业空间高度重叠,如图1所示。由于空间的限制,机器人的实际工作空间被限制在一个狭窄的范围内。这些狭窄的空间是灵活的,尽管机器人不必严格遵守,但人类希望机器人主要在其中活动。上述愿景给机器人的运动控制带来了巨大挑战,主要体现在以下几个方面:(1)机器人任务的动态性。在有人参与的生产线上,由于人为操作和任务变化引入的不确定性,机器人要完成的任务往往不是固定、重复的,这将使传统的离线计划控制方法难以适应任务要求;(2)在部署机器人的过程中,要求快速定义和修改首选领域;(3)在机器人的实时控制过程中,必须同时满足系统的物理约束。

图1 机器人机协作工作场景示例
在已有研究中,基于RRT的轨迹规划方法应用较多。文献[1]在RRT边界探索算法的基础上,引入GFE算法进行细化搜索,并提取连续边界域的形心作为探索目标点,该方法在多机器人协同空间探索任务中效率更高。文献[2]针对传统RRT算法在机械臂的运动规划上缺乏导向性导致收敛速度慢的问题,提出一种扩展点选择策略和自适应步长策略,有效避免了算法陷入极小值。文献[3]提出一种快速探索随机树固定节点算法,该算法在搜索过程中限制节点数,同时对采样节点扩展和父节点选择方法进行了类似的设计。文献[4]提出在生成新点之前先确定父节点可以提高搜索性能,但该方法存在局部最小值问题。
针对狭小的工作空间,主流的规划方法是将空间的限制描述为避障问题。文献[5]提出一种基于水平集的机器人避障方法,其主要思想是用一组几何基元逼近狭窄空间的边界,然后通过组合一组水平集函数得到的不等式约束重新表述避障问题。文献[6]在规划过程中考虑了机器人的运动学模型,构造了运动态势感知图(MSAM),使机器人能够更好地感知周围环境信息以做出最佳决策。文献[7]提出一种基于距离计算和离散检测的路径规划方法。文献[8]针对人工势场法容易出现的局部极小值问题和目标不可达问题进行分析,引入了虚拟障碍物模型,较好地解决了人工势场法的局部极小值问题;文献[9]提出一种基于采样的规划方法,其主要思想是使用基于学习的运动建模方法来预测障碍物,该方法在移动障碍物等较为杂乱的环境中显示出优越性。
近年来,随着深度学习和神经网络的快速发展,智能无碰撞路径规划方法得到了广泛的研究。文献[10]提出一种改进的基于梯度投影的伪逆方法来获得任务空间中的无碰撞轨迹,针对可调增益选择引起的轨迹不连续问题,建立了一种反向传播神经网络来产生更平滑的路径。模型驱动神经网络结合了神经网络的学习性能和自适应性能,以及机器人模型所带来的客观物理规律和稳定性,在机器人控制领域得到了广泛的应用。文献[11]提出一种基于不等式的避障方法,首先讨论了4种不同的QP在线算法,然后在关节速度层面建立了基于LVI的原始对偶神经网络。
在上述研究的基础上,本文作者提出一种基于环境吸引域的新型运动控制与位型优化方法。该方法采用一组关键点定义人类对机器人的预设工作区域,并构建了机器人本体与该关键点集的距离指标;设计了兼顾末端执行器跟踪、环境吸引域指标优化与物理约束不等式的控制问题模型,并建立了递归神经网络进行实时求解。该方法能够在保证机器人末端完成高精度运动控制的同时,使机器人的工作区域尽可能收缩到人类预设的区域,从而有效保证人机协作安全性。
1 问题描述
1.1 机器人模型
不失一般性,文中所考虑的机器人具有串联结构,所有关节都是旋转关节,没有结构柔性。对于自由度为n的冗余机器人,其正向运动学模型可以描述为
x=f(θ)
(1)
其中:θ(t)∈Rn是关节角向量;x(t)∈Rm是描述末端执行器在笛卡尔空间中位置的向量;f(•):Rn→Rm是一个非线性函数,描述了从关节空间到笛卡尔空间的映射。对式(1)求导可得:
(2)

1.2 本体关键点
为了便于对机器人本体位形进行描述,利用机器人本体上的关键点(Body Key Points,BKP)进行表征。如图2所示,通过选取机器人的BKP,可以对机器人本体在笛卡尔空间中的分布情况进行刻画。BKP通常是每个关节中心以及连杆上均匀分布的离散点。
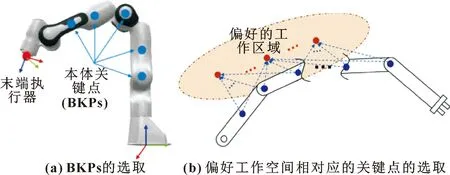
图2 机器人的关键点和环境原理

与BKPs类似,定义关键点集P={P1,P2,…,Pn1}近似描述偏好工作区域,则偏好工作区域与机器人本体之间的广义距离可描述为点集P与K之间距离综合:
(3)
1.3 基于动态规划的初始描述

(4a)
(4b)
θ-≤θ≤θ+
(4c)
(4d)
在实时解决原始动态规划问题时,优化指标与实际需要解决方案的决策变量角速度隐相关。此外,机器人的角速度与优化指标的变化率直接相关。将式(4a)在时间维度上展开,并假设吸引域为静态或准静态,可以得到虚拟吸引力与机器人运动之间的关系:
(5)
在时间维度上对优化指标进行重构,可得:
(6a)
(6b)
θ-≤θ≤θ+
(6c)
(6d)

(7a)
(7b)
(7c)
(8a)
(8b)
(8c)
其中:c1和c2是两个可调的正参数。对于式(8),其高度非线性的性质使机器人的实时控制量获取变得困难。
1.4 控制器设计
提出一种模型驱动的神经网络来实时解决非线性约束优化问题。引入一个用于处理等式约束(8b)的对偶变量λ,拉格朗日函数L可以定义为
(9)
根据Karush-Kuhn-Tucker条件,式(9)的最优解满足
(10)
其中,
(11)
由此可得:
(12)
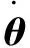
(13)
其中:∈为正参数,主要用于调节控制器的收敛速度。
式(13)为所构造控制器的一般形式。在实际控制过程中,为了尽可能简化控制器,可以选择适当的参数和变量来减少控制器的结构。例如取c2=1,式(13)可以简化为


此处为对提出控制器的进一步讨论。在后面的证明中,为了验证控制器的通用性,仍然选择公式(13)作为对象分析系统稳定性。
1.5 稳定性分析

(14)


(15)
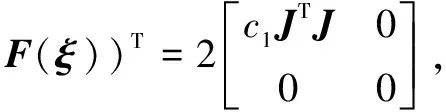
根据F(ξ)的定义,将式(13)进一步改写为
(16)

(17)
对应于式(13)的最优解。
2 数值仿真
分别以平面四自由度机器人与七自由度协作机器人FRANKA PANDA为仿真对象,通过与传统方法的对比,说明文中所提算法的有效性。
2.1 仿真1
以平面四自由度机器人为对象,其各连杆长度为l1=0.296 m、l2=0.296 m、l3=0.296 m、l4=0.212 m;选择机器人每个连杆的中点和节点作为BKP;选取机器人初始关节为θ(0)=[π/2,-π/3,-π/4,0]T;调整控制参数为c1=1、c2=1、∈=0.001、k=5、κ=10,定义机器人的期望轨迹为xd=[0.4+0.1cos(0.5t),0.35+0.1sin(0.5t)]T,并与JMPI方法进行对比。设J-1为雅克比矩阵J的伪逆,并在机器人接近奇异位形时引入阻尼,同时对机器人角速度进行限幅处理。为保证对比试验的一致性,k同样设置为5。对比结果如图3、4所示。对比图3(a)和图3(b)可以看出:两种控制方法都可以跟踪期望的轨迹,收敛时间约为1.5 s,稳态误差分别为2×10-6、2×10-4m,表明所提方法在轨迹跟踪方面与主流方法相差不大。图3(c)和图3(d)为两种算法下机器人关节角度的对比。基于JMPI方法,机器人的关节角1在t=0.8~15 s时间段内超过了物理极限;相比之下,基于文中提出的方法,机器人的关节角度可以保持在最大(小)值,从而保证了系统的安全。在角速度方面,JMPI方法与文中提出的模型驱动方法(图3(f))不同,无法保证仿真初始阶段(图3(e))机器人角速度的有界性(t=0~0.5 s)。

图3 所提算法与JMPI方法在平面四自由度机器人的仿真对比
在此基础上,进一步验证引入环境吸引域优化之后的控制效果。采用[0.3;0.55]作为单一环境吸引域描述点,并选择机器人的关键点1作为吸引对象,仿真结果如图4所示。
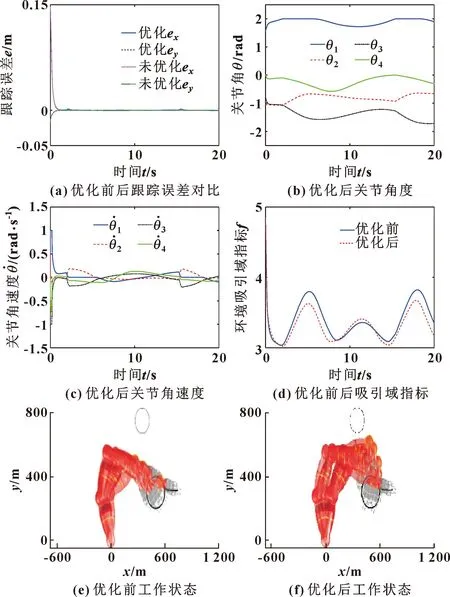
图4 引入环境吸引域前后的平面四自由度机器人仿真对比
由图4(a)可以看出:无论是否考虑虚拟环境优化,机器人的轨迹跟踪误差均收敛于0,收敛时间约为1 s,两种情况几乎没有差异;引入环境吸引域后,机器人关键点到倾斜工作空间的距离对比如图4(d)所示,平均距离从3.6 m减小到3.4 m。引入环境吸引机制后,可以直观地看到机器人的构型变化,机器人的第二个关节进入偏好区域。在这种情况下,机器人的关节角1和关节角2保证了机器人的关键点靠近期望区域,关节角3和关节角4的变化更承担了轨迹跟踪的任务。
2.2 仿真2
为进一步验证所提方法的有效性,选择FRANKA PANDA机器人作为仿真对象。分别选取[0.346 2;-0.675;0.210][-0.253 8;-0.675;0.210]为机器人运动的始末点,以模仿机器人的抓放任务。机器人关节角的初始值为[-0.5;0.33;-1;-1.7;0;2.3;0]rad,空间吸引域的点选择为[0.4;-0.1;0.7]m,实验结果如图5所示。t=0时,机器人末端执行器的位置[0.08,-0.674,0.40]m,相应的跟踪误差约为[-0.25;0;0.2]m。在该控制器的作用下,机器人末端执行器可以快速跟踪期望的轨迹。跟踪误差在t=3.14、6.28、9.42、12.57 s等处存在一定的抖动,这主要是由于机器人在这些点的期望轨迹导数不连续(主要指机器人抓取和放置点时的反向速度,即速度幅值相同但方向相反)。这也证明了所提控制器的适应性,即使在期望轨迹速度不平稳的情况下,系统也能实现高精度的轨迹跟踪。

图5 FRANKA PANDA机器人的仿真结果对比
3 总结
针对冗余机械手同步运动控制过程,提出一种基于环境吸引域的构型优化方法。将人类定义的机器人偏好工作空间简单地建模为一组关键点,并建立一个称为环境吸引域的势函数。在APF方法的启发下,从优化的角度建立一个有吸引力的方案。将物理约束下的运动控制与构型优化问题表述为QP问题,建立模型驱动神经网络实现闭环系统的全局收敛,以软限制的方式在物理约束下同时进行运动控制和构型优化。通过仿真验证了所提方法的有效性。
