低速冲击下混凝土板的能量耗散研究
2023-12-18赵嘉琛任松波杨莉琼
赵嘉琛, 古 松, 任松波, 顾 颖, 孔 超, 杨莉琼
(西南科技大学 土木工程与建筑学院, 四川 绵阳 621000)
我国西南地区因其特殊的地理环境,山区、河流广为分布,且降雨量丰富。因而该地区各类地质灾害频发,其中崩塌落石在所有地质灾害中占比高达17%[1]。由于其突发性、可预见性差、速度快及破坏大等特点,对公路、山区公路防护结构和桥梁上部结构等基础设施造成了严重威胁。
近年来,崩塌落石灾害的频发影响整个西南地区的经济发展及各交通线路的安全性。崩塌落石(Rockfall)[2]是指单个或多个岩块在重力或外力作用下从陡峻岩石山坡上分离并以自由落体坠落、弹跳、滚动或以上组合方式顺坡向下猛烈运动,最后散集于坡脚的一种常见地质灾害现象,如图1所示。

(a) 落石击中大桥
目前混凝土冲击类问题的试验方法包括落锤冲击试验及有限元软件LS-DYNA及ABAQUS数值模拟和SHPB(split Hopkinson pressure bar)杆冲击试验,前者主要应用于混凝土构件在冲击荷载下的结构特性,而后者是对混凝土材料本身在冲击作用下显示的材料性能。古松等[3]通过对混凝土板进行低速冲击试验,得到了冲击力大小受板厚、冲击速度和混凝土强度的影响,推导了考虑结构整体变形的落石冲击力计算方法;王爽[4]利用有限元软件LS-DYNA对框架棚洞受落石冲击进行模拟,得到了冲击深度、冲击力随着冲击能量增大而增大,且盖板损伤区域成“X”状,并随能量增大而增大,提出了拱形棚洞的概念及其工程相关指导意见;张伟[5]针对不同速度的落石冲击,探究了钢筋混凝土板的破坏机理,得到了高中低速冲击破坏的不同机理;王珂[6]利用有限元软件ABAQUS对预加荷载钢筋混凝土板在冲击作用下的动力响应进行研究,得到了钢筋混凝土板受到冲击荷载作用后对系统能量、冲击力以及板中心竖向位移的影响;马钢等[7]分别对素混凝土(plain concrete, PC)梁和纤维混凝土梁进行低速冲击试验,得到了梁类构件的破坏形态为弯曲破坏,且各类纤维混凝土梁比素混凝土梁有着更好的抗冲击断裂性能;赵雪芹等[8]通过对现有国内外对落石冲击力计算方法的整理,推导了一种考虑混凝土板整体变形的冲击力计算方法;Guo等[9]对钢-混凝土组合墙进行低速落锤冲击试验,得到了钢-混组合墙具有良好的抗冲击性能并提出了一种基于能量计算低速冲击下钢-混组合墙最大变形的方法和设计要求与流程;Jones等[10]通过对泡沫混凝土材料进行低速落锤冲击试验,计算了泡沫混凝土吸收冲击能量的能力并得到了泡沫混凝土最佳吸能容量值; Senthi等[11]对钢筋混凝土板在低速冲击荷载下进行试验,显示了所有失效试件都发生冲切破坏,并提出了一种经验公式评估低速冲击下的钢筋混凝土板能量承载能力;党发宁等[12]利用SHPB杆装置探究骨料率和冲击荷载速度对混凝土受冲击的动态力学、变形及能量演化特征,得到了混凝土吸收能量的转化率随骨料率而变化,且吸收能量总是高于裂纹表面能。
以上是国内外学者针对于混凝土板类和混凝土试件展开的一系列低速冲击研究,其中梁类构件主要以弯曲变形失效为主而板类构件的变形较前者更为复杂,涉及整体与局部的变形,且在整个冲击过程中伴随着复杂的能量变化。目前冲击板类构件的研究大都集中于对最大冲击力的计算,而很少针对受低速冲击后板能量耗散的研究。本文将从能量耗散角度研究混凝土板类构件的抗冲击性能,基于前人研究的基础上,通过落锤冲击装置对自配混凝土板试件进行低速冲击试验,探寻混凝土板试件在低速冲击作用下的能量耗散规律,可为后续相关工程建设提供一定指导作用。
1 落锤试验
基于彭丰等的落锤冲击试验的后续研究,下面对试验作简要介绍。
1.1 落锤试验装置
落锤试验装置主要由脚手架搭设平台、落锤、PVC导轨、NOS-F306/50 t冲击力传感器及合成钢冲击头等组成,如图2所示。

(a) 试验原理图
其中落锤质量为40.55 kg,冲击头和力传感器质量为14.1 kg,冲击头直径为13 cm的半球形冲击头。与扁平形相比半球形冲击头能够产生更大的冲击力[13],便于获得更明显的试验结果。
1.2 试验概况及结果
利用自制落锤试验装置对不同板厚、冲击高度以及混凝土强度三个变量进行测试。该试验只考虑冲击的最不利工况正碰[14],即落锤垂直于混凝土板平面进行冲击。试验中对试件板的四边进行简支固定,限制其水平方向和竖直方向的平动。由于试验中所采用混凝土板板厚较薄且为自配混凝土板,无法保证各试件的混凝土强度。因此,为保证试验的准确性,对每个试件混凝土强度进行实测,并采用实测混凝土强度进行分析。
试验中试件的尺寸为边长500 mm,厚度40 mm、80 mm的正方形混凝土板。
落锤冲击试验的结果如表1所示。并选取其中部分混凝土板试件受冲击破坏后的破坏形态图以供展示,如图3所示。

表1 试验结果汇总

(a) 试件h4-05-2破坏形态
2 低速冲击下混凝土板的破坏过程及能量耗散机制
混凝土板在低速冲击作用下破坏变形过程大致分为三个阶段:弹性变形阶段、弹塑性变形阶段以及塑性变形至失效阶段。由此得出,混凝土板受低速冲击破坏作用时,试件吸收的总能量WT主要由3个部分组成:① 混凝土板试件弹性变形能WE;② 混凝土板试件塑性变形能WF;③ 冲击过程中以热能、声波能等形式消耗的能量W0。由能量守恒定律可得
WT=WE+WF+W0
(1)
2.1 试件冲击总能量
在冲击过程中,忽略落锤与空气之间的摩擦,假设混凝土板吸收的总能量WT全部由冲击头释放的重力势能所得,
WT=m落锤gh
(2)
式中:m落锤为40.55 kg;g取9.81 m/s2;h为落锤释放高度。
2.2 混凝土板的弹性变形能
为计算混凝土板的弹性变形能,本文基于弹性力学理论的薄板小挠度弯曲问题计算薄板的最大弹性变形,最后利用应变能广义定义式计算薄板最大弹性变形所需的变形能。
在弹性力学里,两个平行面和垂直于这两个平行面的柱面所围成的物体,被称为平板。两个板面之间的距离δ称为板的厚度,而平分厚度δ的平面称为板的中面。如果板的厚度δ远小于中面的最小尺寸b(如:小于b/8~b/5),这个板就称为薄板[15]。而本文所研究的混凝土板即符合薄板结构的定义,这里取板的中面为xy平面,z轴与xy轴按右手螺旋而垂直于中面,如图4所示。当δ≪l时,对薄板的变形及应力有如下基本假设,通常称为Kirchhoff-Love假设。
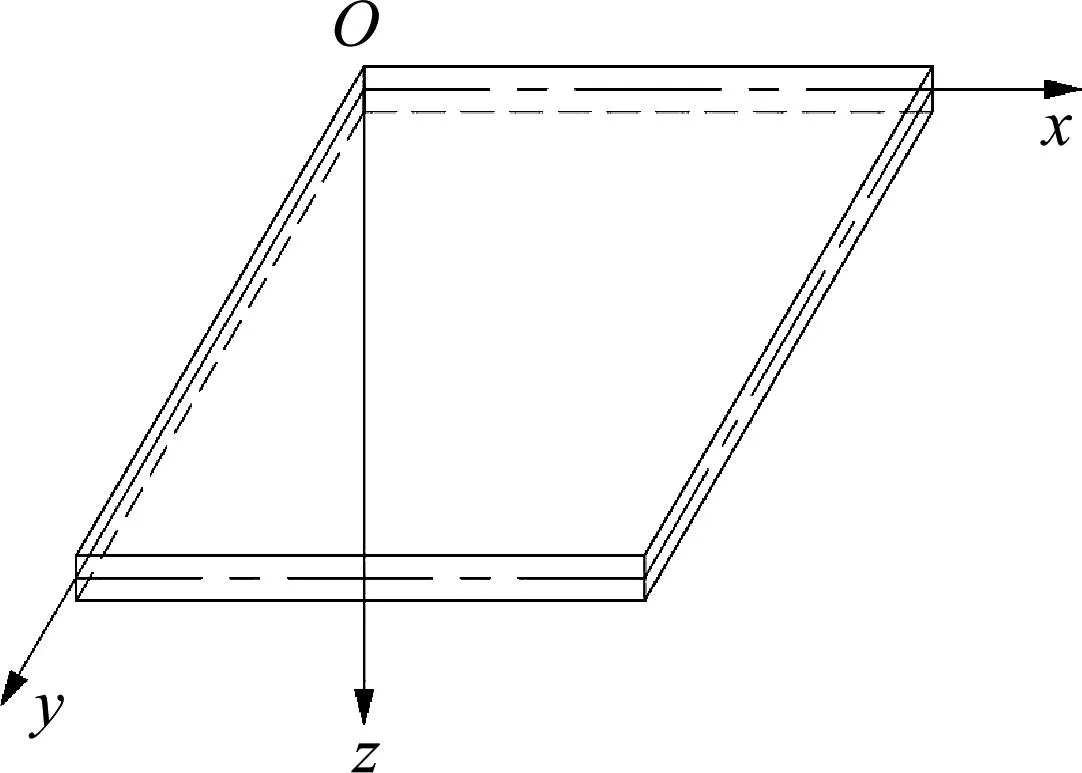
图4 薄板
假设1在板中面上的各点不产生平行于中面的位移。
假设2与中面垂直的法线在变形后仍是直线,并垂直于变形后的中面。
由弹性力学的薄板理论,可以得到以中面挠度w(x,y)表示的弯曲微分方程为
(3)
为研究方便,将落石低速冲击混凝土板简化为四周简支且在板中心受一个集中力P作用的边长为a的正方形薄板弹性变形问题,如图5所示。
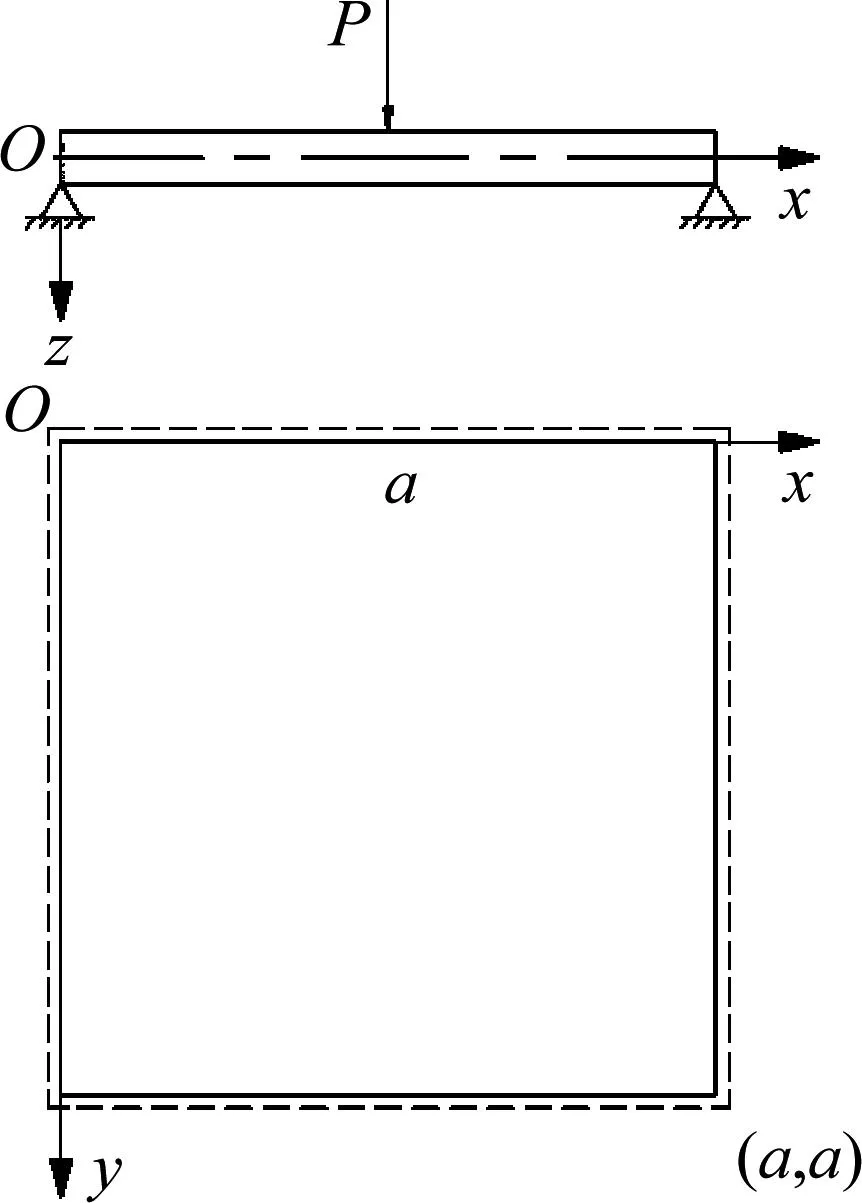
图5 四边简支薄板
将挠曲函数w(x,y)与载荷q(x,y)展开成双三角级数的形式且满足相应边界条件,假设式(3)的解为
(4)
式中,m和n为任意正整数。
系数Amn应由满足式(3)的条件,并将式(4)代入式(3),得
(5)
同时将式(5)右端q(x,y)展开成双三角级数,即
(6)
利用三角函数的正交性,最终可以得到,四边简支板在板中心受一集中力荷载作用下的挠曲方程为
(7)
式中,D为薄板的抗弯刚度
(8)
式中:E为混凝土弹性模量;δ为混凝土薄板厚度;ν为混凝土泊松比,一般取值为0.2.
由于混凝土板各试件的混凝土强度具有离散性,且根据GB 50010—2010 《混凝土结构设计规范》[16]不同强度混凝土的弹性模量E也有一定差异,因此为保证数据的准确性,将各板试件实测混凝土强度和弹性模量E代入式(8),得到每个混凝土板试件的抗弯刚度,如表2所示。
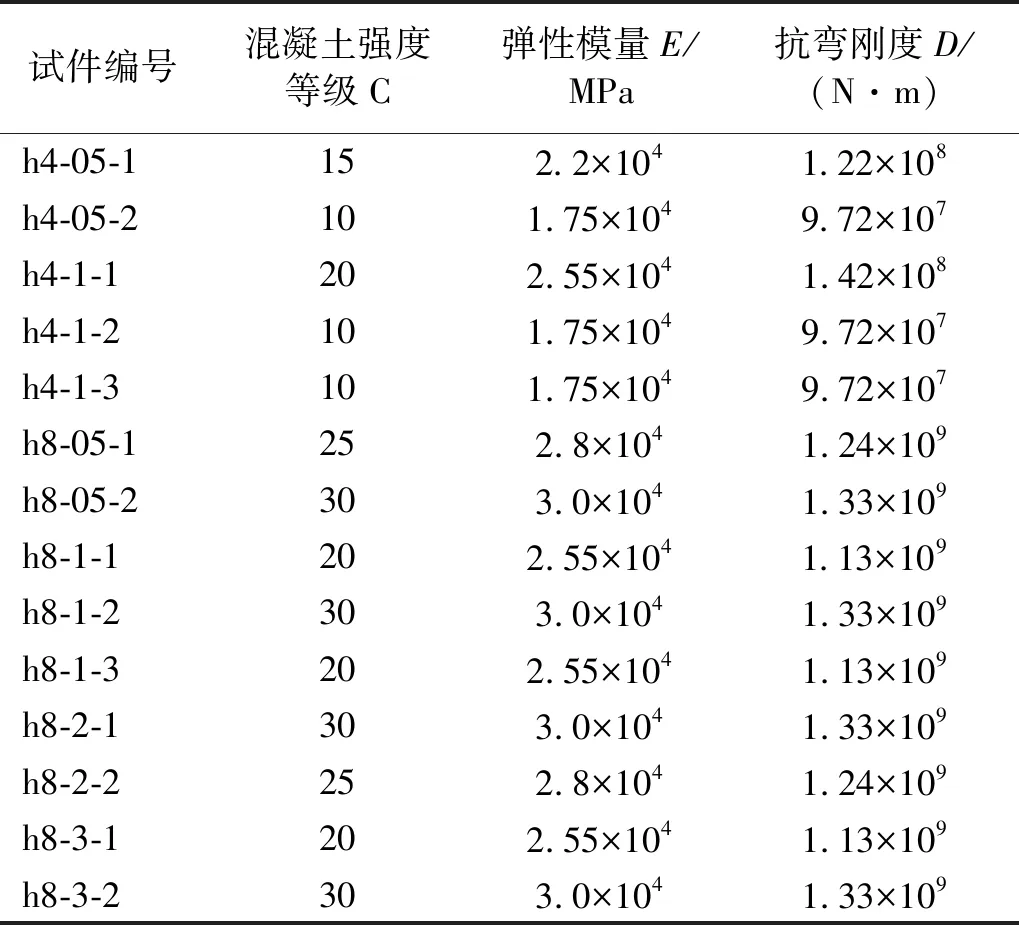
表2 各试件抗弯刚度
构件由于发生弹性变形而储存的能量,表示为Vε,而应变能Vε可以由广义定义式得出
(9)
式中:F为广义力,可以代表一个力、一个力偶、一对力或一对力偶等;Δ为广义位移,可以代表一个线位移、一个角位移或两者的组合等。
薄板的变形主要由下挠并伴随着下挠产生的转角组成。因此,根据应变能广义公式(9)得出混凝土板在受冲击时的弹性变形能大小。

(10)
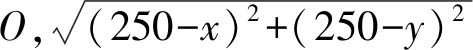
通过MATLAB软件平台,以式(10)为基础公式进行软件编程处理,根据冲击头力传感器上反馈的最大冲击力,将其输入至MATLAB程序中,得出混凝土板在低速冲击作用下的弹性变形能WE的大小,MATLAB软件编程流程图如图6所示。

图6 MATLAB编程流程框图
将落锤试验中所有数据进行统计后,导入各试件的最大冲击力计算后,得到各试件的弹性变形能WE值,计算结果如表3所示。

表3 各试件弹性变形能值
3 混凝土板的能量耗散分析
混凝土板在低速冲击作用下所吸收的总能量WT主要由三个部分组成,即混凝土板试件弹性变形能WE、混凝土板试件塑性变形能WF以及冲击过程中以热能、声波能等形式消耗的能量W0。
第2章中对混凝土板弹性变形能的计算可得,在低速冲击作用下混凝土板弹性变形能占比极低,而吸收总能量大部分都通过塑性变形能而进行耗散。在文献[17]中可知,各混凝土板试件破坏形态是以冲击点为中心向四角呈放射状贯穿裂缝,这种径向裂缝表明了板件的弯曲性能[18];而部分混凝土板试件在冲击中心出现锥状孔洞,这一现象说明了混凝土板在冲击作用下也表现出冲切破坏的特征。
本文中研究的板件为素混凝土组成,而混凝土材料的脆性特征决定了混凝土板在弯曲变形超过其弹性变形极限后,随即进入塑性变形过程,其塑性变形的过程主要表现为初始缺陷的扩展和新生裂缝的产生。
在低速冲击作用下混凝土板超过其弹性变形极限后至失效的过程中随着裂缝的发展和新生,混凝土板沿主裂缝形成塑性铰线并沿着铰线转动以消耗落锤的冲击能量。而岩石试件断裂过程中吸收的总能量主要用于断裂、损伤能量和碎片飞溅的动能[19]。因此,假设混凝土板试件塑性变形能WF是由混凝土板试件初始缺陷(微裂缝、微孔洞)扩展、新生成裂缝以及受冲击时试件飞溅碎块的耗能构成的。通常认为,在加载速率不是特别高的情况下,以热能、声波能等形式消耗的能量W0很小,可以忽略[19]。将式(1)化简后表示为
WT=WE+WF
(11)
由式(11)并结合表3,得出混凝土板试件在低速冲击作用下的塑性变形能大小。
由表4可知,混凝土板在低速冲击作用下板试件吸收总能量WT基本上都转化为塑性变形能WF,除了h4-05试件组,其余各试件组的WF/WT比率高达99%。

表4 各试件塑性变形能
Zhang等[20]的试验中定量计算了试件吸收总能量WL和飞溅碎块动能WE,在静态断裂的WFD/WL几乎在100%(WFD为岩石断裂和损伤能),而在动态冲击加载时,WFD/WL会随着冲击速度的增加而减少。翟越等[21]的冲击试验中通过对花岗岩与混凝土分别进行冲击压缩试验分析出混凝土试件破坏时,吸收能量的至少85%用于裂纹的扩展和发育。
本文试验中冲击的最大速度都在10 m/s以内属于典型的低速冲击,且冲击头的刚度远大于混凝土板试件。因此,在冲击过程中混凝土板塑性变形能占比更大。以上学者的研究在本文试验结果同样能够得到类似的体现,进一步验证了计算结果的有效性。
3.1 混凝土强度与塑性变形能
为更好分析两者之间的关系,将选取试件h4-1-1~h4-1-3和试件h8-1-1~h8-1-3,并从表1得到以上各试件的混凝土强度值。混凝土强度与其塑性变形能关系曲线,如图7所示。
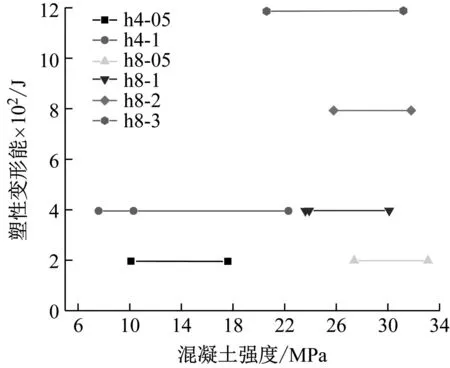
图7 混凝土强度与塑性变形能关系曲线图
h4试件组塑性变形能WF为395.600 6~396.157 1~396.030 1以及h8试件组WF为388.211 2~384.968 87~385.883 1,两个试件组的数据浮动值都小于1%,说明了混凝土板低速冲击作用下塑性变形能的大小不完全受混凝土强度影响。
PC板由于:① 本身组成材料的特性(开裂即失效);② 无配筋的约束作用,导致在冲击作用下的变形主要表现为整体弯曲变形和局部冲切破坏。本文由于试验的冲击速度都不大,因此局部冲切破坏并不明显,而占据主导地位的是整体弯曲变形。弯曲变形的受力特征是构件上部受压、下部受拉,PC各强度下的抗拉强度相差不大且很低。因此,在低速冲击作用下PC板的PC强度的改变对其塑性变形能的大小无明显的影响。
3.2 冲击能量与塑性变形能
为了得出冲击能量对混凝土板试件的塑性变形能的影响,这里将选取试件组h8作为研究对象。根据式(2)可计算出各试件所受的冲击总能量WT,并绘制PC板冲击能量WT与其对应塑性变形能WF关系曲线图,如图8所示。
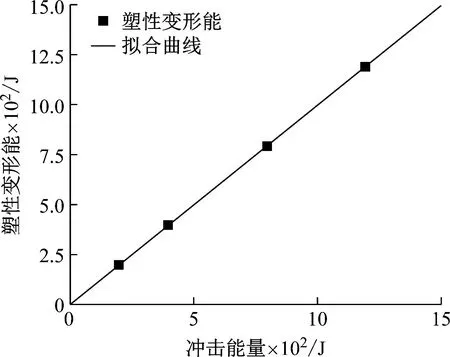
图8 冲击能量WT与塑性变形能WF关系曲线图
由于自配PC板试件PC强度存在较大的离散性,会对研究准确性造成影响,因此选取h8-05-1、h8-1-1、h8-2-2、h8-3-2作为研究对象,它们之间的PC强度误差在10%以内,能够最大程度地减小PC强度离散性对研究的影响。
由图8可知,PC板的塑性变形能WF随着冲击能量WT的增大而增大,并且增长趋势呈现线性关系。并将图中h8数据组进行拟合,得到关于冲击能量WT与板件塑性变形能的拟合函数,即:
WF=0.15+0.99WT
(12)
式中:WF为试件塑性变形能;WT为冲击能量。
该式仅限于四边简支固定的PC板在中心处受冲击荷载时由式(10)和式(11)所计算的试件塑性变形能WF与其冲击能量WT之间的函数关系。
该式的Pearson指数为1,说明了PC板的塑性变形能与冲击能量有很好的线性关系。在低速冲击作用下,冲击能量的大小决定着PC板塑性变形能的耗散。式(13)中0.15代表在中心处受静载作用下PC板的塑性变形能,而0.99则代表塑性变形能WF随着冲击能量WT变化的速率。
4 结 论
本文在落锤低速冲击试验研究的基础上,对PC板冲击破坏过程和能量耗散机制进行了理论推导和参数分析,得到了以下结论:
(1) PC板在低速冲击作用下的冲击过程主要经历了三个阶段,即:弹性变形阶段、弹塑性变形阶段及塑性变形阶段、试件失效破坏阶段。而PC板在经历短暂的弹性变形阶段后,便进入了弹塑性及塑性阶段,而PC板的破坏主要发生在第二阶段,因此第二阶段是混凝土板类构件研究的重点。
(2) 在低速冲击作用下,PC板吸收的全部冲击能量主要通过塑性变形(该过程伴随着初始缺陷(微裂缝、微孔洞)扩展、新生成裂缝以及受冲击时试件飞溅碎块)的方式进行耗散,且塑性变形能占到整个冲击能量的95%以上。
(3) PC板在低速冲击作用下,PC强度对其塑性变形能无明显影响作用;而冲击能量WT对PC板的塑性变形能有明显的影响作用,根据拟合可以得出冲击能量WT与其塑性变形能WF有着很好的线性关系。
