基于FxRLS自适应逆补偿的振动控制策略研究

王 敏, 廖松泉, 钟雨轩,3

(1.上海大学 机电工程与自动化学院,上海 200444; 2.上海大学 海洋智能无人系统装备教育部工程技术研究中心,上海 200444; 3.上海大学 计算机工程与科学学院,上海 200444)

随着空间探索的不断发展,航天器运行时的微振动环境成为影响其搭载的高精度设备性能的重要因素。空间微振动具有振幅小、频带宽等特点,传统的被动隔振无法满足对中低频振动的有效控制。目前的隔振手段,通常采用在被动结构中引入主动控制的方式实现高性能隔振[1-2]。

振动主动控制是一种有源隔振,其通过次级通道引入主动控制力来抑制或削弱传递到负载端的振动,具有适应性强和隔振效果好等优点[3]。振动主动控制的核心和关键,是控制策略的设计与研究,其直接关系到最终的控制效果。振动控制目前存在多种方法,如积分力反馈控制[4],相位补偿控制[5],反馈与前馈复合控制[6],自适应控制[7-8]和前馈逆补偿控制[9]等。其中基于自适应滤波的主动逆补偿控制方法,采用自适应响应跟踪,进行主动逆补偿振动消除,具有较好的振动响应的跟踪和消除能力,其控制结构简单且对模型参数的变化不敏感,因此应用广泛[10-12]。

在自适应滤波控制中,最小均方(least mean square, LMS)算法和最小递归二乘(recursive least squares, RLS)算法是振动和噪声主动控制领域最受欢迎的算法[13]。在实际隔振系统中,由于次级通道的存在,LMS和RLS算法中对权向量的调整异常敏感,影响控制算法的计算效率。为消除次级通道的不良影响,通常采用改进的带次级通道的FxLMS算法[14-15]和FxRLS算法[16-18]进行振动和噪声的主动控制。

目前对LMS和RLS等自适应滤波算法的研究,多侧重于算法特性和结构改进方面的理论研究[19-20],而很少涉及与隔振装置结合后算法的响应跟踪和振动消除效果的讨论。相较于FxLMS算法,FxRLS算法在跟踪速度和跟踪精度两方面的综合性能更优,但存在运算数据量大的不足。随着计算能力的不断提升,计算量大将不再是制约其应用的重要因素。因此,将基于FxRLS的自适应逆补偿振动控制策略应用于隔振系统中的研究变得更有价值。

本文将基于FxRLS自适应逆补偿的振动主动控制策略应用于一个单自由度隔振系统,从隔振系统动力学模型和自适应逆补偿算法两方面分析了系统的振动消除机理。通过自适应控制算法对系统响应进行精确跟踪,利用逆补偿控制对系统振动进行主动消除。为了进一步校验控制策略的有效性,本文在Simulink和试验环境中,搭建了验证系统,并对结果进行了分析。

1 隔振系统模型

在振动控制中,隔振需求可分为单自由度隔振和多自由度隔振。多自由度隔振系统通常由一个负载平台、一个基础平台和若干单自由度隔振单元以特定构型组成,其振动控制问题经过结构和算法的解耦可以转换成多个独立自由度振动控制问题,简化了自适应逆补偿控制策略的分析。

因此,非一般性本文以单自由度隔振为研究对象,搭建的隔振系统,如图1所示。它由一个力传感器、一个压电致动器、一个弯曲片弹簧和两个用于连接两个平台的柔性铰链组成。压电致动器具有定位精度高、刚度大的特点,为了降低系统的整体等效刚度,本文将其与具有相对较低刚度的弯曲片弹簧串联使用。该隔振系统结构简单紧凑,可根据不同应用场合需要,利用柔性铰链连接为多自由度隔振系统。

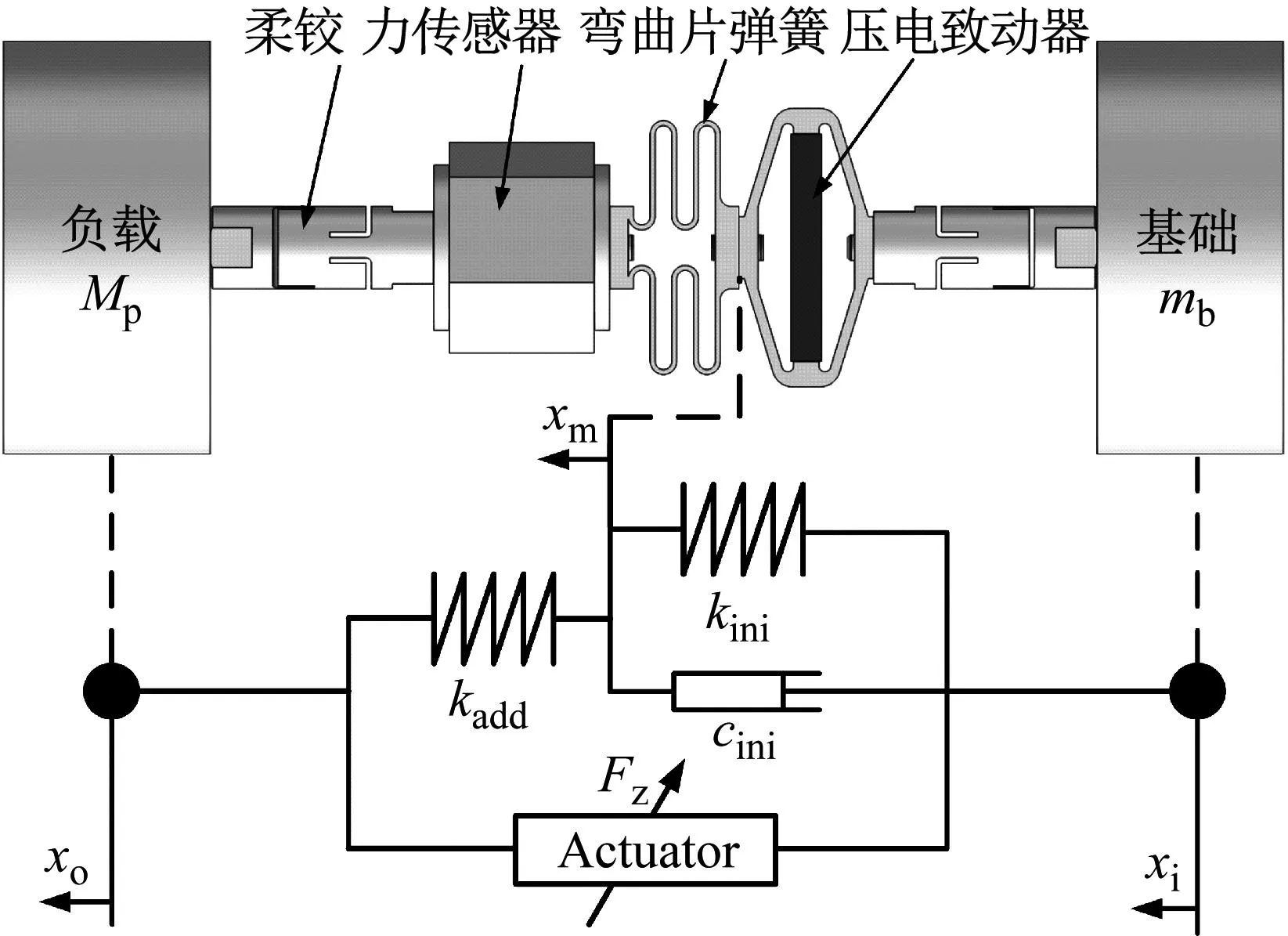
图1 隔振系统结构和等效模型图

根据图1中的等效模型,本文隔振系统的动力学方程为

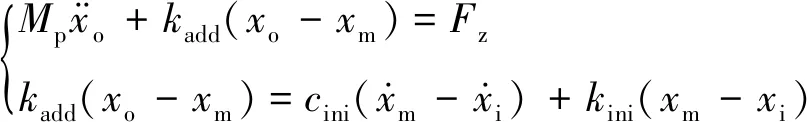
(1)

将式(1)中两式拉氏变换后联立,消去中间连接点xm处的相关变量,得到隔振系统代数方程的动力学模型为

(2)

将式(2)与弹簧-阻尼系统的模型进行等效可得:c=kaddcini/(cinis+kadd+kini)为系统的等效阻尼,kd=kaddkini/(cinis+kadd+kini)为系统的等效刚度,两者都随外部激励变化。考虑本文中的隔振装置为小阻尼系统,其初始阻尼cini在数值上远小于初始刚度kini,系统的等效阻尼与等效刚度可以合理的简化为c=kaddcini/(kadd+kini)与kd=kaddkini/(kadd+kini)。

将等效阻尼与等效刚度代入式(2)移项整理

(Mps2+cs+kd)-1[(cs+kd)Xi+Fz]=

Xo(e→0)

(3)

由式(3)可知,引入自适应逆补偿振动主动控制的目的是产生与传递的基础扰动相位相反的补偿力Fz,使得负载端响应(即残余振动e)趋近于零。

2 面向振动消除的自适应逆补偿控制

2.1 自适应逆补偿控制结构

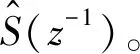
图2 自适应逆补偿控制框图

控制策略中的横向滤波器的抽头权向量W(n)能够根据残余振动e(n)和滤波后的参考信号x′(n)随时间进行迭代更新,从而达到对振动响应实时自适应逆补偿的效果。

在第n时刻,滤波器的输出信号是过去输入信号的加权组合,即

(4)

式中,N为滤波器的阶数

(5)

估计误差定义为滤波器输出与实际传递直接扰动的差值,由于次级通道S(z-1)的存在,负载的实际残余振动误差为

e(n)=y(n)-S(z-1)Fz(n)

(6)

2.2 FxLMS算法逆补偿控制律

FxLMS算法基于均方误差最小准则,其抽头权向量的代价函数定义为

ζ(n)=E{e2(n)}

(7)

该算法采用最速下降法对取得代价函数极小值点的抽头权向量进行迭代搜索。由于代价函数的最速下降方向是函数曲面的负梯度方向,最速下降法可表示为

(8)

式中,u为步长因子。为了适应于实时控制,采用瞬时误差平方值代替代价函数,最终得到抽头权向量的递推公式为

W(n+1)=W(n)+μe(n)x′(n)

(9)

从式(9)可知,抽头权向量新息的更新主要依靠步长因子u,参考信号x′(n)和误差信号e(n)三项。

2.3 FxRLS算法逆补偿控制律

FxRLS算法基于最小二乘准则将抽头权向量的代价函数定义为

(10)

基于逆补偿的自适应滤波算法的目标是找到一组最优权值,使代价函数取得最小值,即代价函数的梯度为零。代价函数的梯度可写为

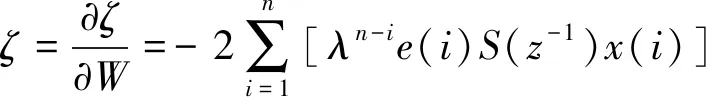
(11)

根据以上分析,令式(11)等于零,整理得

W(n)=R-1p

(12)

式中:R为x′(n)的平均自相关矩阵;p为y(n)和x′(n)的平均互相关矩阵。

自适应控制系统中的数据是实时更新的,每次更新,W(n)都需重新计算,计算量很大,为了进行实时控制,根据RLS相关理论可推出W(n)更新的递推公式

W(n)=W(n-1)+g(n)e(n)

(13)

其中,

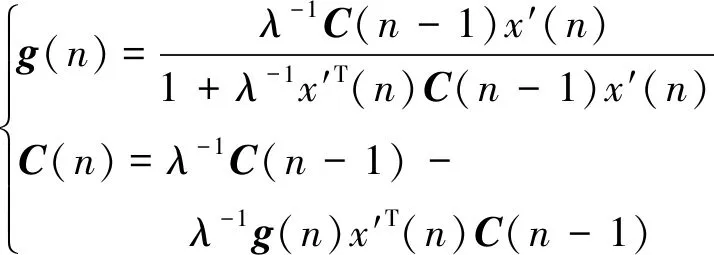
(14)

式中:g(n)为增益矢量;λ为遗忘因子;C(n)为逆平均自相关矩阵。FxRLS算法的初始化设定为W(0)=0,C(0)=δ-1I,δ是一个极小正常数。

比较FxLMS算法和FxRLS算法控制律公式可知,FxLMS算法计算简单,便于进行实时逆补偿控制,但由于FxLMS算法采用瞬时误差代替均方误差,利用随机梯度下降法搜索最优值,控制器的抽头权向量在最优值邻域内游走,因此在振动消除过程中存在收敛速度缓慢和稳态误差较大的不足。

FxRLS算法采用加权误差平方和代替均方误差,使用观测区间内信号的时间平均代替集平均,当随机振动信号具有各态遍历性时,控制器的抽头权向量随着迭代次数的增加能够精确且快速的收敛于最优值。因此,FxRLS算法能有效解决FxLMS算法的以上问题。

3 仿真算例

3.1 仿真参数设置

为了校验基于自适应逆补偿主动控制策略的隔振系统的有效性,本文综合上文推导的隔振系统动力学模型和自适应逆补偿算法公式,在Simulink环境中对隔振系统在不同激励下的跟踪性能及振动消除效果进行了分析。隔振系统仿真参数设置如表1所示。

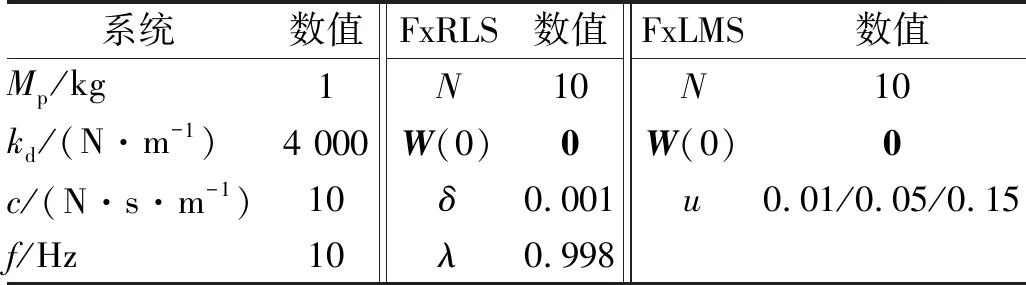
表1 仿真参数设置

3.2 响应跟踪与误差

频率取0.1 Hz、1 Hz、10 Hz、20 Hz、50 Hz和100 Hz的正弦激励下的响应跟踪效果曲线,如图3所示。依次为幅值相同,从跟踪速度和跟踪精度两方面对隔振系统的响应跟踪能力进行评估,跟踪效果曲线各关键参数如表2所示。其中稳定时间和误差幅值可综合反映响应的跟踪速度,而稳定误差和跟踪率则用于反映响应的跟踪精度。

表2 不同激励信号下跟踪效果

图3 正弦激励跟踪效果曲线

定义跟踪率为负载端的逆补偿输出稳态幅值与振动响应稳态幅值的百分比,即

从图3(a)和图3(b)可知,在低于隔振系统固有频率的低频激励范围,LMS和RLS均能较快的达到稳定跟踪状态,但此时RLS的误差幅值明显小于LMS,表明RLS具有更快的跟踪速度。例如在0.1 Hz正弦激励下,两者的稳定时间均为约0.4 s,LMS的误差幅值为0.056 μm,而RLS的误差幅值仅为0.005 μm。从稳定误差对比两种算法,RLS在稳定后能够近乎无误差的跟踪激励信号,稳定误差小于0.31×10-3μm,而LMS由于采用随机梯度的原因,存在失调的现象,跟踪稳态误差出现周期性波动,幅值达到了7.68×10-3μm,且随着激励频率的增加而加剧。

从图3(c)～图3(f)可知,在正弦激励频率大于等于隔振系统固有频率的中高频段,以10 Hz正弦激励为例对比发现,两者的稳定时间均为约0.6 s,LMS的误差幅值为5.16 μm,RLS的误差幅值为5.02 μm,RLS相较LMS仍然具有更快的收敛速度,能迅速的将跟踪误差衰减到稳定值,但两种算法稳定后的稳态误差相同,均为约0.207 μm,即跟踪精度相同。与低频激励比较可以发现,中高频正弦激励下两种算法的跟踪稳态误差均没有收敛于零值,而是存在周期性波动。从跟踪率可知,随着激励频率的增加,该周期性波动的占比也增加,跟踪精度下降。例如100 Hz正弦激励下,LMS和RLS的稳态误差为0.008 μm,跟踪率为60.98 %。

正弦混合信号(混合频率为1 Hz、10 Hz、50 Hz和100 Hz)和1 Hz三角波信号激励下的响应跟踪效果曲线,如图4所示。从图4(a)和表2可知,LMS的稳定时间、误差幅值和稳态误差分别为1.3 s、5.45 μm和0.35 μm,而RLS则分别为0.5 s、5.00 μm和0.21 μm,RLS相比于LMS在跟踪速度和跟踪精度方面均具有明显优势,反映了多频周期混合信号会影响LMS的跟踪性能,而RLS则能在一定程度上克服该问题。同理,从图4(b)和表2可知,三角波激励下RLS在收敛速度和收敛精度上同样均优于LMS。

图4 混合信号和三角波信号激励跟踪效果曲线

因此,RLS算法在基于自适应逆补偿的振动响应跟踪中表现出更优的性能。

3.3 时域与频域振动消除响应

为直观反映应用RLS自适应逆补偿主动控制策略的隔振系统的隔振效果,对隔振系统控制前后的负载端时域响应以及频域响应进行分析,如图5所示。

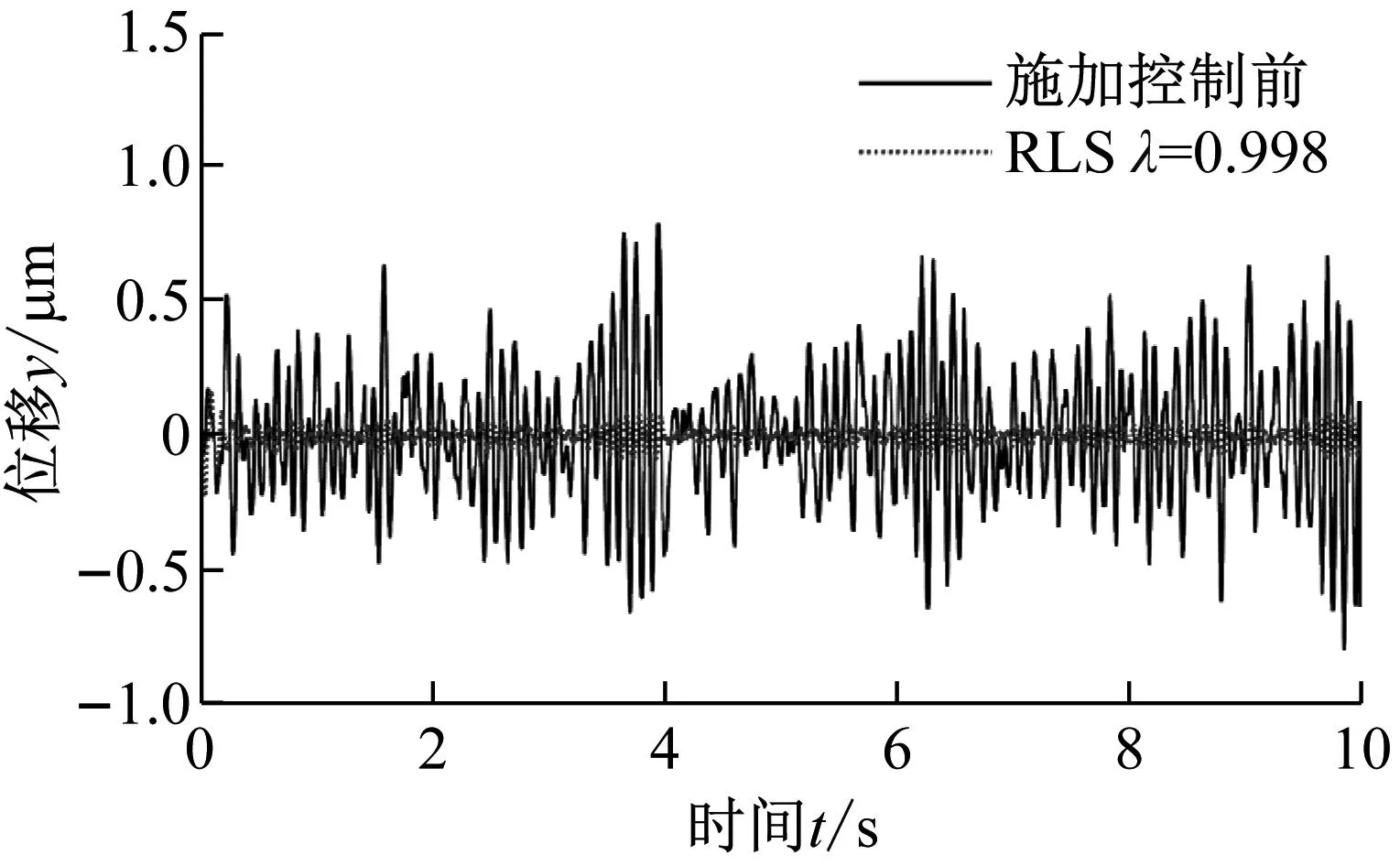
(a) 时域响应

从图5(a)可知,主动控制施加前,隔振系统负载在随机激励下的响应最大值为0.8 μm,均值为0.25 μm,主动控制施加后最大值变为0.225 μm,均值变为0.034 μm,振动衰减0.575 μm和0.216 μm,隔振率分别达到71.9 %和86.4 %。

从图5(b)中的系统幅频特性曲线对比可知,绿色区域为隔振性能改善区,应用自适应逆补偿控制后隔振系统在中低频段的振动幅值得到显著抑制,反映出系统在中低频段具有更好的逆补偿效果,例如振动在0.1 Hz处衰减了24.9 dB,在共振峰(10 Hz)处衰减了17.3 dB。因此,应用基于RLS自适应逆补偿的振动主动控制策略,可以有效拓宽系统的低频隔振带宽,克服被动隔振系统中低频隔振性能不足的劣势。

4 振动衰减试验

4.1 试验平台搭建

搭建隔振性能试验平台如图6所示。该试验平台包括单自由度隔振系统样机、实时控制系统与频谱分析系统。为模拟航天器中微重力下的微振动环境,隔振系统样机采用水平悬挂的方式安装。隔振系统中采用压电致动器(PSt150)与压电驱动器(E00.A6)实现主动补偿力的输出。实时控制系统的核心是NI控制器(NI PXI-1042Q),其实时收集经过调制的力传感器(PCB 208C02)的残余振动信号和加速度传感器(PCB 356A14)的基础振动信号,并将经过算法计算产生的控制信号输出给压电驱动器。频谱分析系统由两个外部加速度传感器(PCB 356A17)与LMS频谱分析仪(LMS SC-XS06-E)组成。激振器(JZ-2)通过LMS生成信号和功率放大器(GF-50) 放大信号输出随机噪声激励,模拟环境微振动。外部加速度传感器采集基础和负载的振动信号给LMS处理,完成振动的采集与分析。

图6 隔振性能试验平台

4.2 振动衰减效果

隔振系统在不同控制条件下负载时域响应曲线的对比图,如图7所示。

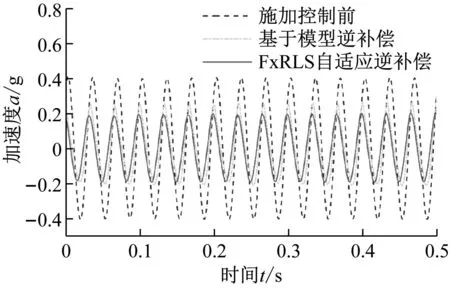
(a) 正弦信号激励

由图7(a)可知,正弦信号激励下,负载加速度响应控制前的幅值为±0.41g,应用基于固定模型的逆补偿控制后变为±0.30g,幅值衰减0.11g,隔振率27 %;应用本文基于FxRLS自适应的逆补偿控制后变为±0.24g,幅值衰减0.17g,隔振率42%。由图7(b)可知,随机信号激励下,负载加速度响应控制前幅值的均方根为0.03g,最大幅值为0.08g,应用基于固定模型的逆补偿控制后分别变为0.02g和0.064g,均方根值衰减0.01g,最大幅值衰减0.016g,平均隔振率33.3%;应用基于FxRLS自适应的逆补偿控制后分别变为0.01g和0.04g,均方根值衰减0.02g,最大幅值衰减0.04g,平均隔振率66.7%。

对比可知,根据前文建立的隔振系统模型,采用本文基于FxRLS自适应的逆补偿控制策略取得的振动衰减效果优于基于模型固定的逆补偿控制策略。

5 结 论

为有效消除航天器中微振动对高精密设备的不利影响,本文将FxRLS自适应控制算法与逆补偿控制方法结合的振动主动控制策略应用于单自由度隔振系统中。从隔振系统动力学模型和自适应逆补偿算法两方面分析了系统的振动消除机理,并在Simulink和试验中构建了控制模块与机械模块一体的验证系统,根据结果可得:

(1) 在低于隔振系统固有频率的低频段,RLS和LMS在正弦激励下的稳定时间相同,RLS的误差幅值小于LMS,证明RLS具有更快的跟踪速度。同时,RLS的稳定误差小于LMS,跟踪率大于LMS,而LMS存在周期性波动,且随着激励频率的增加而加剧,则证明RLS具有更好的跟踪精度。同理,在正弦激励频率大于等于固有频率的中高频段,RLS具有更快的跟踪速度,跟踪精度与LMS相同。与低频不同,中高频正弦激励下两种算法的跟踪稳态误差均存在周期性波动。随着激励频率的增加,LMS和RLS的跟踪率从0.1 Hz处的99.97%变为100 Hz处的60.98%,即跟踪精度下降。

(2) 在正弦混合信号激励下,LMS的稳定时间、误差幅值和稳态误差分别为1.3 s、5.45 μm和0.35 μm,RLS则分别为0.5 s、5.00 μm和0.21 μm,RLS相比于LMS在跟踪速度和跟踪精度方面均具有明显优势,反映了多频周期混合信号对RLS跟踪性能的影响小于LMS。同理可证明RLS对三角波信号的跟踪效果优于LMS。

(3) 在本文控制策略应用前后,隔振系统频域响应在0.1 Hz处振动衰减24.9 dB,在共振峰处衰减17.3 dB,有效消除了负载振动且中低频段效果更好。在随机激励下的负载时域响应中,仿真结果显示响应均方根值从0.25 μm变成0.034 μm,振动衰减0.216 μm,隔振率86.4%。试验结果则显示响应均方根值从0.03g变成0.01g,振动衰减0.02g,隔振率66.7%。试验与仿真均证明了自适应逆补偿控制策略的有效性。