考虑SSI效应的下一代大型海上风力机抗震控制研究
2023-12-18秦志豪戴靠山
余 洁, 秦志豪, 杨 阳,, 戴靠山
(1.宁波大学 海运学院,宁波 315211; 2.四川大学 灾变力学与工程防灾四川省重点实验室,成都 610065)
地震灾害一直是影响风力机正常运行的重要因素,海上风电支撑结构较陆上风力机更长,因而地震会加剧对塔架振动的影响。我国海上风电场靠近东部负荷中心,就地消纳方便,可以最大程度发挥其优势,缓解当地用电压力[1]。但东部沿海地区位于环太平洋地震带,受制于地理因素,地震频发,因此海上风力机塔架设计时需考虑地震载荷作用[2]。
对于地震作用下的风力机动力响应,国内外学者开展了大量研究。Yan等[3]考虑非线性土-构耦合(soil-structure interaction,SSI)效应,研究了单桩式、三脚架式和夹套式10 MW风力机在风-浪-流-地震联合作用下的结构动力学响应。Chen等[4]提出叶片-机舱-塔架-基础耦合模型,通用人工鱼群算法对调谐质量阻尼器(tuned mass damper,TMD)进行参数优化,并对参数优化后的风力机动态响应进行研究。牛凯伦等[5]对DTU 10 MW风力机构建多物理场模型,研究了风力机极端环境下的动力响应特性和混沌特性。李志昊等[6]通过建立不同桩-土耦合效应模型对DTU 10 MW单桩风力机地震动力学响应进行研究。薛世成等[7]基于精确桩土模型对NREL 5 MW桁架式风力机在风-地震联合作用下的结构动力学响应和结构控制进行研究。
上述文献中研究对象仍以5 MW和10 MW风力机为主,为降低海上风电运营成本,实现平价上网,就必须增大风力机单机容量,提高风能利用效率,因此,大型化将会成为未来风电发展的主要方向之一。梅轩等[8-9]研究了风-浪-地震联合作用效应以及SSI效应对15 MW海上风力机地震动力响应的影响特性,结果表明风力机结构抗震设计应考虑SSI,地震显著增强了15 MW风力机塔顶振动和塔基载荷,需要对其进行抗震控制从而降低结构振动幅度和载荷。
为此,本文通过对开源软件FAST进行二次开发,考虑SSI效应建立了地震条件下通用的海上风力机动力学分析及控制模型,以IEA 15 MW单桩式风力机为研究对象,研究了地震载荷对海上风力机结构动力学响应的影响,并基于TMD控制方法,对地震作用下的风力机进行减载抑振研究,结果对风力机结构抗震设计具有参考价值。
1 研究对象
1.1 IEA 15 MW风力机模型
为满足于下一代风力机研究需求,美国能源可再生实验室与丹麦科技大学在国际能源署的资助下,联合设计了一台专门用于海上风电研究的15 MW单桩风力机,即IEA 15 MW风力机[10],如图1所示。

图1 IEA 15 MW单桩式海上风力机
该风力机单桩直径为10 m,叶片长度为117 m,叶片质量为6.5 t,是目前公开用于学术研究的最大尺寸的风力机。其额定风速和转速分别为10.59 m/s和7.56 r/min,对应的设计尖速比为9,最大叶尖速度为95 m/s。塔架高度为144.495 m,质量为1 017 t,下部单桩重量为1 318 t。
1.2 土-构耦合模型
由于地震发生时,土壤柔性特征更为明显,刚性基础假设存在一定误差。为获取更准确的风力机地震动态响应特性,通过耦合弹簧模型表示土壤与结构的相互作用,耦合弹簧模型考虑土壤与结构的相互作用,如图2所示。平动及转动方向均存在三个线性弹簧,表征土壤反应力。

图2 土-构耦合模型
假设土壤为典型硬土,其剪切模量Gs和泊松比νs分别为140 MPa 和0.4。各方向的SSI模型弹簧刚度可表示为[11]
(1)
(2)
(3)
(4)
(5)
(6)
式中:Kx、Ky和Kz分别为纵向、横向和垂向刚度;Krx、Kry和Krz分别为横摇、纵摇和艏摇方向刚度;h和r0分别为单桩泥面下长度和半径,其值分别为45 m和5 m。
2 研究方法
2.1 地震载荷计算方法
为了解决大质量法的局限性,通过修改FAST中风力机动力学方程,实现了土木工程中广泛应用的模态加速度地震载荷计算方法,从而考虑地震载荷与其他环境载荷的联合作用。在FAST中,单桩基础和塔架视为一个整体支撑结构,并采用线性模态法对其进行结构动力学建模。风力机地震动力学分析流程,如图3所示。在风-浪-震联合作用下第i阶模态自由度的动力方程如下
(7)

图3 风力机地震动力学分析流程图


(8)
式中:H为支撑结构的长度;ρ(h)为支撑结构的质量密度;φi(h)为支撑结构第i阶归一化模态振型。本文考虑了支撑结构前后及侧向的前两阶模态,其中一阶模态阻尼比为0.5%,二阶模态阻尼比为1%。
在地震荷载计算中,风轮和机舱被简化为支撑结构顶端质量mRNA。其相应的地震荷载Feq.RNA为
Feq.RNA=aeq·mRNA
(9)
2.2 TMD控制方法
为了减缓海上风力机在地震荷载作用下的动态响应,本文基于TMD开发了被动结构控制模块。TMD的基本概念是通过在适当位置放置质量阻尼器来吸收外部激励的能量。本文将两个独立的TMD垂直放置在塔顶,以减轻由于地震荷载引起的支撑结构的纵向和侧向运动响应。
通过修改FAST中的风力机运动学和动力学计算部分的源代码,实现多荷载作用下的TMD控制。将TMD运动产生的力加入到广义力中,每个方向上的TMD力FTMD推导如下
(10)

(11)
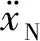
2.3 有效性验证
为验证本文所建立的地震分析模型、SSI模型和TMD控制模型的有效性,与风电一体化仿真领域知名的软件Bladed和OpenFAST(v3.4)进行比较。
首先,计算了风力机在不同地震波作用下的塔顶纵向位移变化,与Bladed比较结果如图4所示。从图4可知,在所有地震波工况下,本文计算结果均与Bladed结果吻合十分良好,由于二阶模态阻尼不同而导致了轻微的幅值差别。

(a)
其次,计算了风-浪载荷作用下的塔顶位移和泥面处弯矩,与OpenFAST比较结果如图5所示。从图5可知,本文模型计算的塔顶位移变化规律与OpenFAST结果完全一致,在部分地方存在轻微的幅值差别,泥面处面外弯矩计算结果类似。导致这一偏差的主要原因是OpenFAST v3.4对FAST v7中的气动计算模型进行了较大程度的改善,对于动态失速和动态入流条件下的气动力计算精度均得到了一定的提升。因此本文模型计算的结果与OpenFAST结果存在一点偏差,但偏差并不大,位移最大值偏差1.3%,弯矩最大值偏差4.8%。

(a)
最后,通过计算塔架在TMD控制作用下的自由衰减运动曲线,与OpenFAST计算结果进行比较,塔顶纵向位移和TMD轨迹变化如图6所示。从图6可知,本文建立的TMD控制模型计算结果与OpenFAST v3.4计算结果几乎完全一致,塔顶位移的衰减规律和TMD的位移变化均与OpenFAST结果十分吻合,验证了TMD控制模型的有效性。
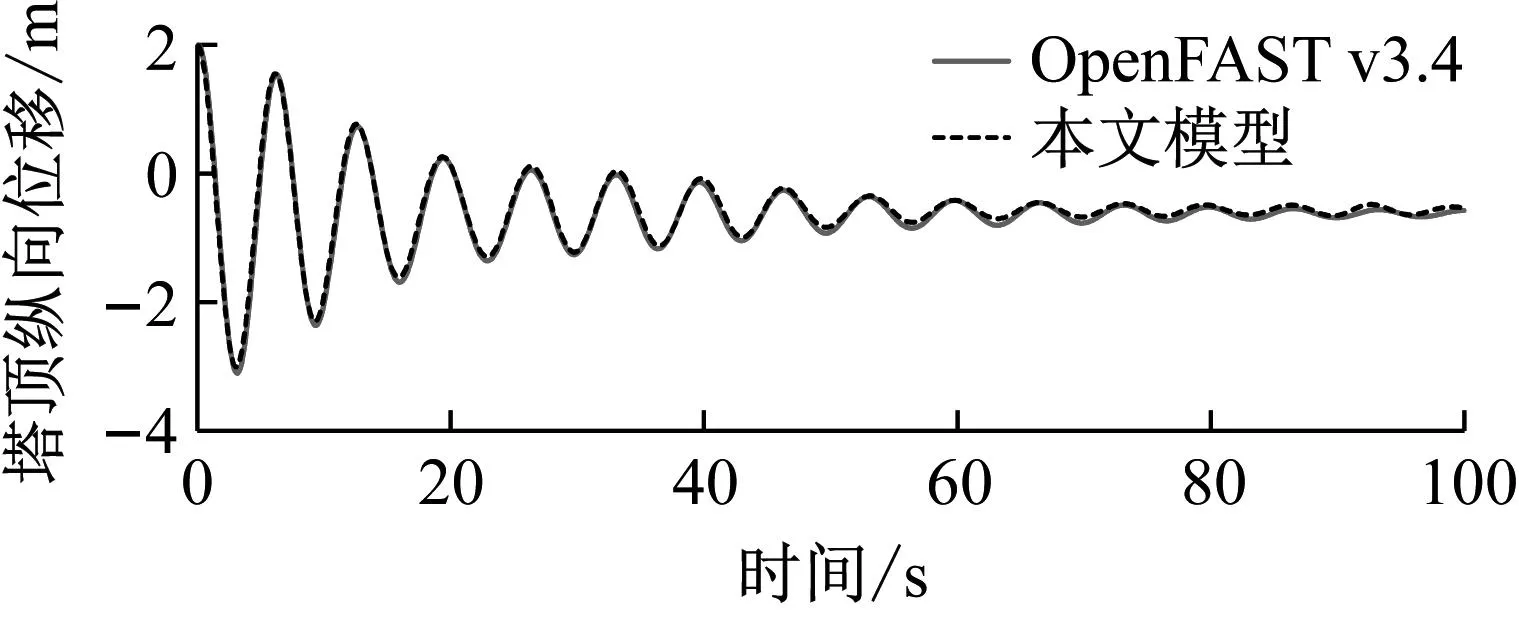
(a)
(b)
3 仿真工况
3.1 环境载荷
本文通过TurbSim生成湍流风场,该风场平均风速为10.88 m/s,时长为1 000 s,图7为轮毂高度处风速分布。通过P-M谱定义非规则波浪频率分布,有义波高和谱峰周期分别为1.5 m和7.7 s,假设波浪方向与风向一致。

图7 不同时刻轮毂高度处风速分布
选取了1940年发生在美国帝王谷的El Centro地震,里氏震级为6.9级,图8为El Centro地震加速度。

(a)
3.2 TMD控制参数
一般地,TMD减振效果与质量大小成正相关,但过大的TMD质量会增大成本。因此,本文选择TMD质量比为3%,即塔架支撑结构总质量的3%,TMD质量为43 671.94 kg。调谐频率比λ为0.8,阻尼比ξ为10%,TMD刚度和阻尼分别为46 421 N/m和8 901.4 N/(m/s)。
由于塔架主要以一阶振动为主,TMD需放置在模态位移最大处,因此将TMD置于塔顶。通过计算塔顶振动和塔基载荷,并与无TMD控制时结果比较,从而分析TMD的控制效果。
4 结果与分析
每个算例仿真时长为800 s,时间步长为0.002 s,为避免风力机瞬态行为的影响,在第600 s时加入地震激励。
4.1 风-浪-地震载荷下耦合响应
为研究地震荷载对IEA 15 MW单桩风力机耦合响应的影响,选用三种不同荷载场景,如表1所示。其中风、浪荷载方向与地震x分量方向相同。
图9为IEA 15 MW风力机在三种载荷条件下的塔顶位移时域变化。

(a)
由图9可知,仅地震工况下,风力机塔顶的纵向位移和侧向位移呈现周期性波动,且幅度较大。塔顶前后位移和侧向位移的变化范围分别为-1.27~0.13 m和-2.81~2.67 m,极差分别为1.40 m和5.48 m,可以明显看出塔架侧向振动更剧烈。耦合载荷导致的前后塔顶位移在-0.22~1.76 m的范围内变化,大于仅地震条件下的变化范围,说明在地震发生时风载荷和波浪载荷会加剧地震激励时风力机塔顶振动。但在地震结束后(大于650 s),耦合载荷条件导致的塔顶纵向位移极差为1.17 m,仅地震条件下塔顶纵向位移极差为1.31 m,表明风荷载与波浪荷载减轻了地震结束后塔架振动。当风力机在风-浪联合作用下运行时,塔顶位移在0.49~1.34 m的范围内波动,与其他两种载荷场景中的波动相比小得多,说明风浪引起的振动比地震引起的振动要轻得多。在地震结束后,耦合载荷下风力机塔顶纵向位移曲线逐渐与风-浪联合作用下的曲线拟合,说明地震结束后风力机塔架纵向振动主要受风载荷与波浪载荷影响。
通过对风力机塔顶加速度结果进行快速傅立叶变换,并对变换的结果进行常用对数转换后,乘以20,得到单位为dB的塔顶加速度的频谱图,如图10所示。

(a)
由图10可知,在耦合载荷与仅地震载荷情况下,塔顶纵向加速度均在0.17 Hz时达到峰值,分别为-7.57 dB和-6.67 dB,耦合载荷的纵向频域响应略低于仅地震工况。同时由于风力机侧向无风,塔顶侧向加速度频域曲线在耦合荷载和仅地震条件下高度拟合,一阶固有频率处的峰值大小相近,这说明在地震作用下,风荷载和波浪荷载对风力机塔顶振动影响较小。此外,风-浪条件下塔顶加速度的幅值明显小于其余两种荷载条件下的幅值。这一结果说明地震是塔架振动的主要荷载。
为进一步比较地震载荷对风力机结构动力学影响大小,计算了塔架位移最大值随塔架高度的变化趋势,如图11所示。
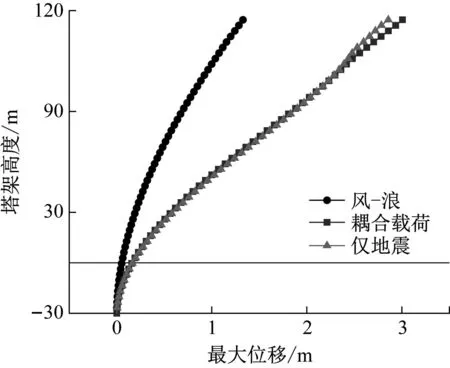
图11 三种载荷下风力机塔架不同高度处位移最大响应
从图11可知,仅地震条件下的塔顶位移与耦合载荷条件下的塔顶位移基本相等,且远远大于仅地震荷载情况的塔顶位移。耦合荷载引起的塔顶位移超过3.0 m,与风-浪条件相比地震使塔顶位移增大55.8%,这意味着地震激励引起的塔架振动幅度远远大于风-浪荷载引起的弹性变形。
4.2 TMD控制
4.2.1 风-浪-地震工况
上述结果表明,地震荷载显著增强了塔顶振动。为了降低地震荷载可能造成的结构损坏,采用TMD减轻地震作用下海上风力机塔架振动。有无TMD情况下塔顶位移与塔基弯矩时域响应,如图12所示。
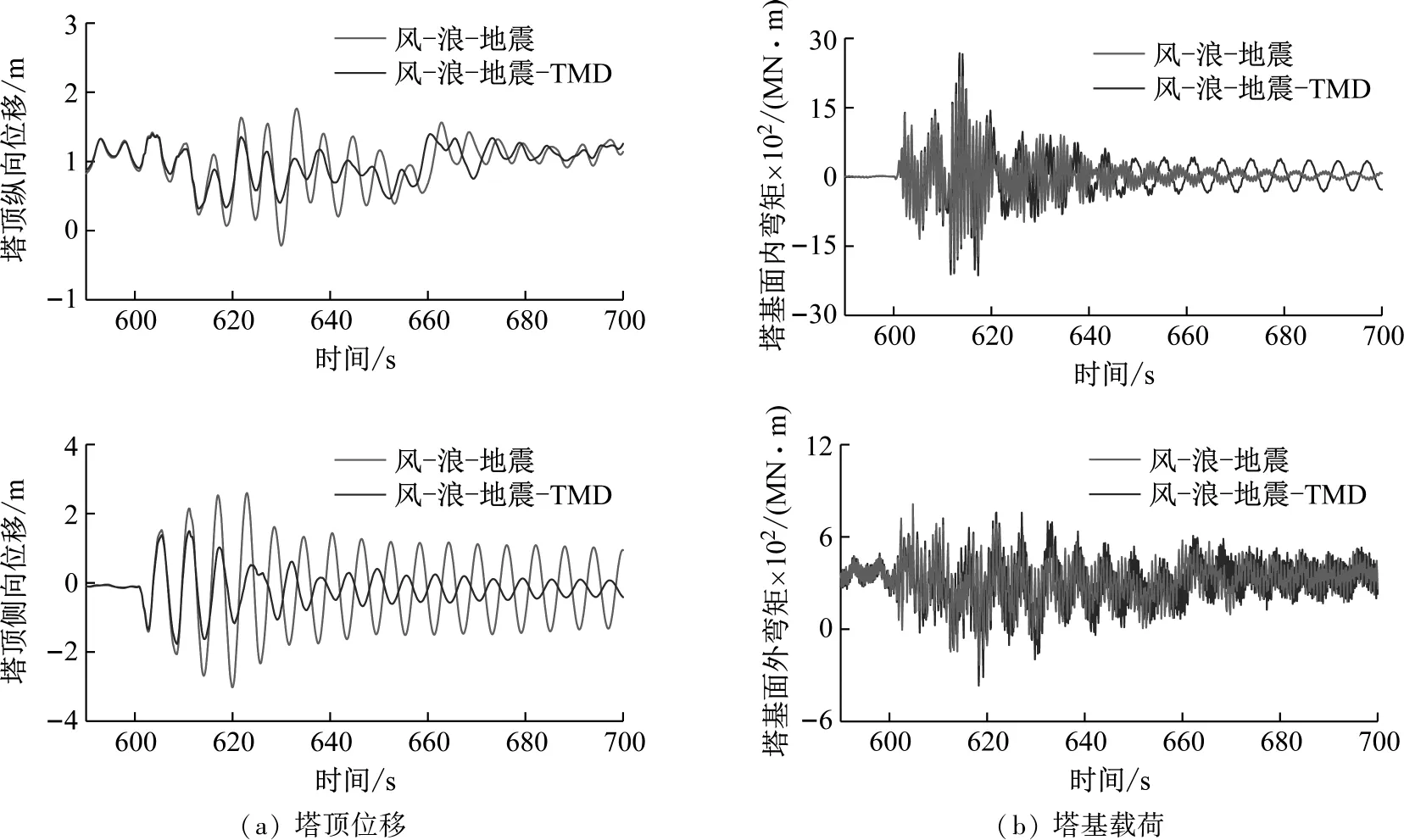
图12 塔架时域响应
由图12(a)分析可知,TMD显著缓解了塔架振动,塔顶纵向与侧向位移峰值分别降低了20.5%和42.4%,标准差分别降低了31.6%和53.5%,由图12(a)可知,TMD在消除地震引起的塔顶侧向位移波动方面更为有效,从而使塔顶运动轨迹的范围更窄。由图12(b)可知,塔基面内弯矩峰值降低18.8%,面外弯矩峰值增加7.1%,标准差分别降低12.4%和14.2%,TMD无法有效降低塔基载荷峰值,尤其是面外弯矩。但TMD可以显著降低地震后的塔基面内弯矩,在650~800 s期间的面内弯矩标准差从206.2 MN·m降至55.2 MN·m,降低幅度超过70%。
通过对图12中的时域结果进行快速傅里叶变换,可以得到塔顶位移与塔基载荷频谱,如图13所示。

图13 塔架频域响应
从图13(a)可知,风浪条件下塔顶振动尤其是塔顶侧向振动不明显。地震发生后,地震载荷使得塔架一阶固有频率(0.17 Hz)处振动急剧增大。加入TMD后,塔架纵向及侧向一阶固有频率(0.17 Hz)处峰值均显著降低,峰值分别由0.19 m降低为0.08 m,0.98 m降低为0.14 m,降低幅度达57.9%和85.7%。由图13(b)可知,TMD显著降低了塔架一阶固有频率(0.17 Hz)处的响应幅值,一阶固有频率处的面内弯矩幅值从165.1 MN·m降低为49.2 MN·m,降低幅度达70%;对面外弯矩的影响较小,一阶固有频率幅值降低了53%。
通过计算塔架位移最大值随塔架高度的变化趋势,如图14所示。从图14可知,TMD有效的减少了塔架位移峰值,尤其是塔顶位移,与无TMD情况相比最大位移降低33%,说明了TMD抑制塔架振动的有效性。

图14 风力机塔架不同高度处位移最大响应
4.2.2 无地震工况
为进一步分析TMD的控制效果,计算了无地震工况下,不同风速工况有无TMD控制时的塔架位移和载荷时域波动,通过比较TMD控制和无TMD控制时200~700 s区间内的塔顶位移及塔基弯矩最大值,分析TMD的控制效果。图15为不同风速下塔顶位移和塔基弯矩最大值统计结果。从图中可以看出,TMD对于塔顶前后位移的控制效果十分有限,这是因为这一方向在强烈的风载荷作用下,产生了较大的弹性变形,而载荷波动引起的振动幅值相对较小,因此TMD的作用不甚明显。相反地,TMD可以有效降低塔顶的侧向位移,特别是高风速情况下,由于气动载荷波动较大,风轮转速也较高,产生了较为显著的侧向载荷波动,引起了塔顶侧向振动。在TMD控制下,塔顶侧向位移的最大值得到了较为明显的抑制,对于大部分工况其降低幅度均超过30%。
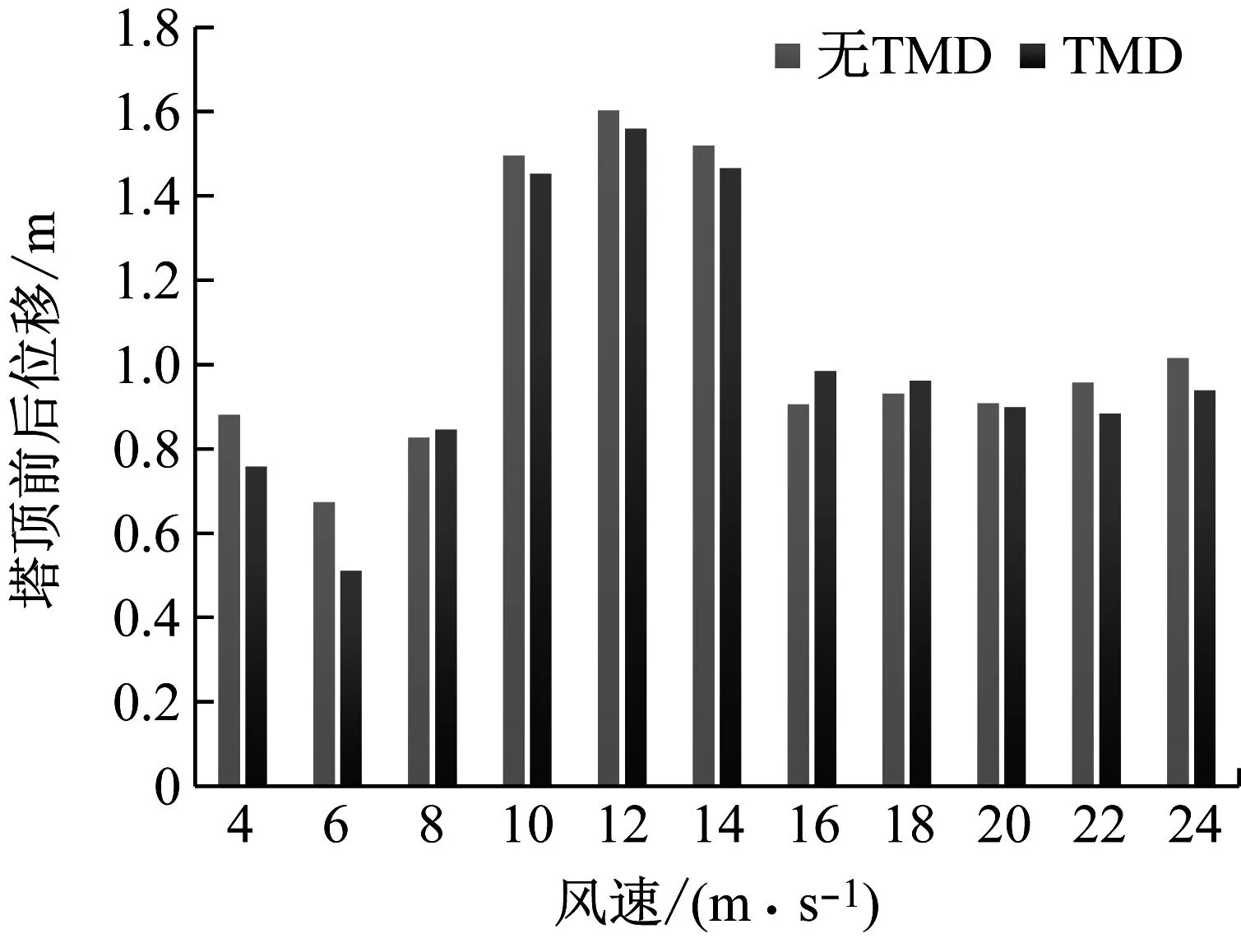
(a) 塔顶前后位移最大值
TMD对于塔基弯矩的作用与塔顶位移相似。由于面内弯矩由侧向推力引起,而面外弯矩主要受到纵向推力影响,因此TMD对塔基面内弯矩的作用与塔顶侧向位移相似,较为明显地降低了面内弯矩的最大值。而对塔基面外弯矩的作用效果则与塔顶前后位移相同,几乎没有明显作用。
5 结 论
本文对开源软件FAST二次开发,考虑SSI建立海上风力机地震动力学仿真及控制模型,研究了El Centro地震波与风-浪荷载联合作用下的15 MW风力机结构动力响应以及TMD的减振效果,结果表明:
(1) 在El Centro地震波作用下,地震载荷是风力机塔架振动的主要因素,风载荷与波浪载荷对风力机影响较小,但对地震后塔顶纵向位移影响较大。
(2) TMD可以有效降低塔架振动,对塔顶侧向位移尤为明显,可降低El Centro地震波作用下的塔顶侧向位移峰值40%以上。
(3) 在El Centro波工况下,TMD可以有效降低地震后塔基面内弯矩波动幅度,最高降低比例可达73.2%。塔架一阶固有频率处的弯矩幅值同样显著降低,降幅超过70%。
