导流板旋向对螺旋铜管换热器传热性能的影响

2023-12-18季家东倪旭旺张经纬李飞扬陈清华

振动与冲击 2023年23期

季家东, 倪旭旺, 张经纬, 李飞扬, 陈清华

(1.安徽理工大学机械工程学院,安徽淮南 232001;2.安徽理工大学人工智能学院,安徽淮南 232001)

用于提高换热器换热效率的强化传热技术细分为有源强化技术、无源强化技术和复合强化技术[1-2]。流体诱导振动强化传热[3-5]不需要消耗额外的能量,是一种典型的无源强化传热技术,也是换热设备实现强化传热常用的典型手段。螺旋铜管(helical copper tube,HCT)换热器[6]基于流体诱导振动实现强化传热的技术理念,将内部传热元件从传统钢管置换为HCT,充分利用流体冲击HCT引发的振动实现强化传热。由于内部HCT和壳、管程进出口布置的局限性,使流体在壳程流域的流动规律性较差,导致换热器的综合传统性能不高。通过在壳程流域内安装螺旋导流板(spiral deflector,SD)可有效改善流体流径[7],进而实现对换热器综合传热性能的提高。因此,探究不同安装方式的SD对换热器内HCT振动和传热性能的影响,实现SD的最优布置规划,具有重要的理论和工程意义。

换热器内铜制传热元件流体诱导振动和振动强化传热方面。Ji等[8-11]对传统平面盘状铜管传热元件在壳程诱导下的振动强化传热机理进行了系列研究,研究发现:平面盘状铜管在壳/管程流体的诱导下呈现出小幅低频振动的特性,且阵型主要呈现为面外振动;壳程流体是引起传热元件振动的主导因素。姜波等[12]提出了一种新型平面盘状铜管传热元件,并对其在壳、管程流体耦合诱导下的传热特性进行了试验和数值研究,研究表明:平面盘状铜管的换热主要集中于内侧管束,且小配重块侧的传热性能优于大配重块侧。Duan等[13-14]基于场协同机理对传统平面盘状铜管传热元件的强化传热性能进行了分析,分析提出:场协同效应及振荡相对速度是产生强化传热的关键,且流速的增大会引起强化传热性能的降低。HCT换热器方面,Wang等[15]分析了结构参数对HCT热应力和传热性能的影响,分析指出:热应力在管束应力分布中占主导地位,通过结构优化使换热器的平均综合性能提高了57.64%。

通过在换热器内安装折流板或导流板,可明显提高换热器的综合传热性能。Bayram等[16-17]研究了折流板间距对一种小型管壳式换热器传热性能的影响,研究发现:不同折流板间距方案下壳程流场的温度分布和传热速率具有明显的差别。基于具有不同倾角的SD,Chen等[18]对一种油-水换热器的传热性能进行了数值分析,分析表明:当SD倾角为12°时,传热系数和综合指数分别比具有相同压降的分段折流板高出47%和51%。Arani等[19]研究了组合类型折流板对换热器传热性能和压降的影响,研究表明:具有组合型折流板的换热器的压降较传统单一折流板换热器的压降有所增加,但传热性能有很大的提高。

为获得具有更高综合传热性能的HCT换热设备,基于两种导流方案的换热器:SD、HCT同旋向换热器(记为:SSD-HCT换热器)和SD、HCT反旋向换热器(记为:OSD-HCT换热器),采用双向-流固耦合(fluid solid interaction,FSI)计算法,研究了SD旋向对HCT振动强化传热性能和换热器综合传热性能的影响。

1 模型和方法

1.1 HCT换热器

SSD-HCT换热器和OSD-HCT换热器的示意图,如图1所示。为便于标注,将换热器从中间截断。

图1 SSD-HCT换热器和OSD-HCT换热器示意图

对于SSD-HCT换热器,4个SD和4根HCT等螺距同向螺旋。对于OSD-HCT换热器,4个SD和4根HCT等螺距反向螺旋,为了不影响HCT的振动性能,在SD上设置多组开孔,使HCT与SD间隙配合。HCT均布安装在左、右管板上,SD与换热器壳体和中空管无缝连接。壳程流体由右侧壳程入口流入,通过壳程入口管直接流入换热器壳体,经SD的导流作用螺旋前进,冲刷HCT后从左侧壳程出口流出。管程流体从底部管程入口流入左侧封头,通过管板上设置的开孔流入HCT,经右侧管板上设置的开孔流入右侧封头,最后从顶部管程出口流出。

1.2 计算域及网格

流体域方面,壳程流体是引起传热元件振动的主导因素,本文流体域仅保留壳程,如图2(a)所示。结构域方面,除HCT材料为紫铜外,其余部分材料均为不锈钢,因钢制材料在流体诱导下的振动十分微弱,结构域仅保留4根HCT,如图2(b)所示。

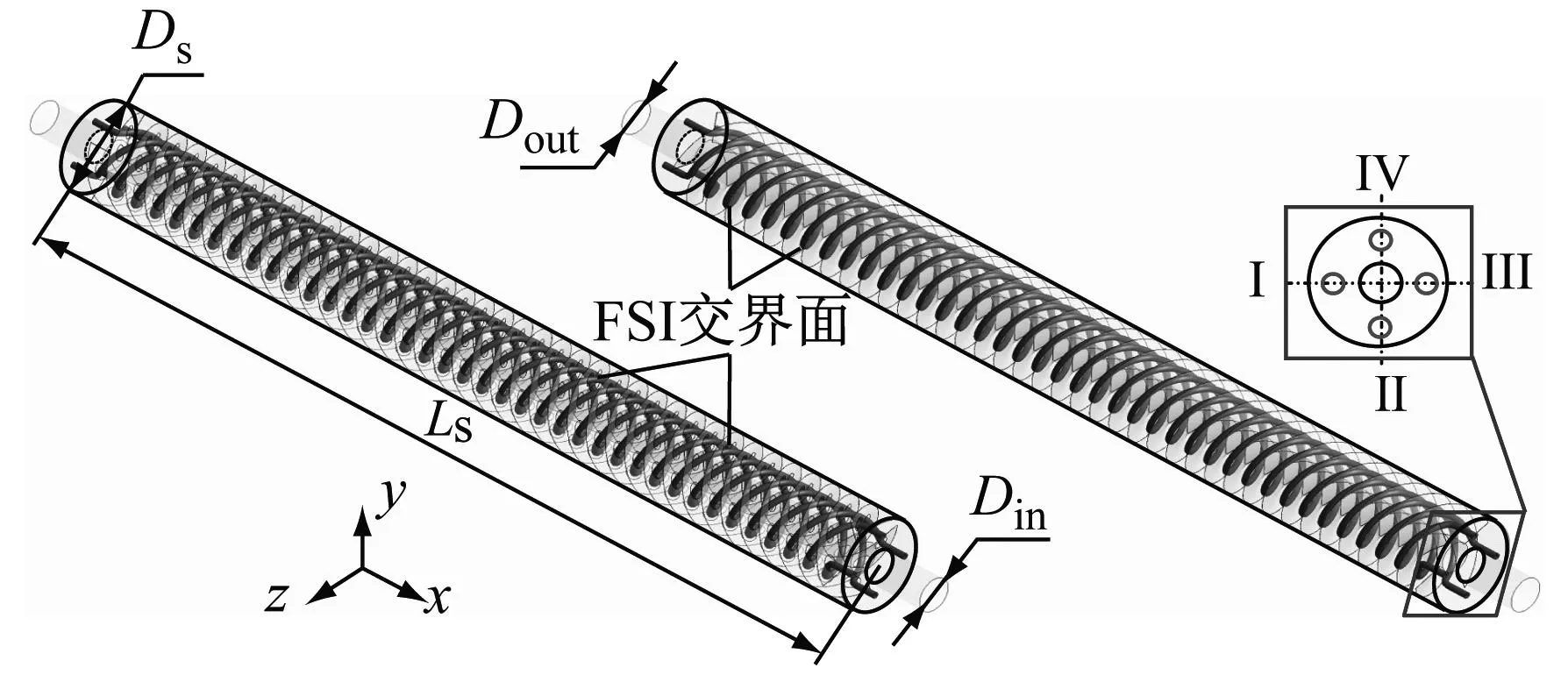
(a) 流体域

图2(a)中:Ls为壳程流体域长度;Ds为流体域直径;Din、Dout分别为流体域入口和出口直径。4根HCT沿逆时针方向依次编号为I、II、III、IV。流体域内与HCT接触的壁面为FSI交界面。

图2(b)中:LT、LH分别为HCT总长度和螺旋部分长度;DH为HCT螺旋直径;DT、δ分别为HCT的外径和壁厚。为分析HCT的振动响应,设置监测点PI、PII、PIII和PIV,其与HCT端面距离为LM。HCT的物性参数标识为:密度ρ、弹性模量E、泊松比ν。结构参数和物性参数取值如表1所示。

表1 结构参数和物性参数的取值

结构域和流体域网格,如图3所示。网格划分采用ANSYS Workbench平台的Meshing网格划分模块完成。

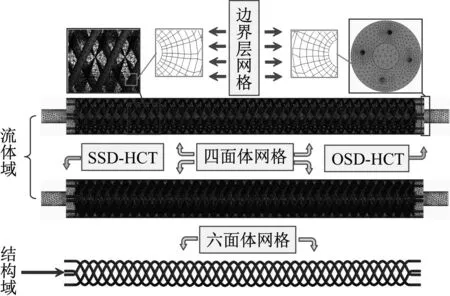
图3 结构域和流体域网格

结构域采用六面体网格,单元数为12 800,节点数为89 760。流体域采用四面体网格,并在靠近FSI交界面处设置了6层边界层网格,SSD-HCT换热器流体域的单元数和节点数分别为7 982 008和1 490 193;OSD-HCT换热器流体域的单元数和节点数分别为8 079 896和1 509 596。经验证,这种网格划分策略满足网格无关性的要求,具体验证过程参见“1.6网格独立性及计算方法论证”。

1.3 计算方法

计算采用粗算&精算策略,计算模块选择Workbench平台的CFX模块(执行流体域计算)和Transient Structural模块(执行结构域计算)。具体计算流程如图4所示。粗算:基于初始边界条件,采用CFX模块执行流体域计算;精算:基于流体域的粗算结果数据和结构域的初始边界条件,执行双向-FSI计算。精算时,CFX模块和Transient Structural模块交替运行,通过FSI交界面传递压力和位移数据。

图4 粗算&精算计算流程

基于流体域的边界条件设置(参见“1.4 边界条件”),计算选择标准k-ε湍流模型,迭代残差设为10-5,具体控制方程参见文献[9]。计算过程中,设置粗算时间为300 s,时间步长为0.2 s;精算时间为1.2 s,时间步长为0.001 s,结构域和流体域的计算时间和时间步长一致。

1.4 边界条件

结构域:HCT端面均设为固定约束;HCT外表面设为FSI交界面;重力方向设为“-y”,设置重力加速度值为9.81 m/s2。

流体域:流体介质设为水;入口设为速度入口“Inlet”,设置入口流体速度(uin=0.05 m/s,0.20 m/s,…,0.65 m/s)和恒温度(Tin=293.15 K);出口设为压力出口“Outlet”,设置出口压力(Pout=0)。与HCT接触的壁面设为FSI交界面,参见图2(a),设置壁面温度(TF=333.15 K);其余壁面均设为非滑移绝热壁面。

1.5 数据处理

HCT的传热性能通过努塞尔数Nu表征,表达式如下

Nu=hDT/k

(1)

式中:k为导热系数;h为面均传热系数,其表达式如下

h=q/ΔT

(2)

式中:q为热流量;ΔT为对数平均温差,其表达式如下

(3)

式中,Tin、Tout、TF分别为入口流体温度、出口流体温度和FSI交界面温度。

4根HCT的平均传热性能通过平均努塞尔数Num表征,其表达式如下

(4)

式中,下标i为HCT编号,i=I、II、III、IV。

换热器单位压降的传热性能通过单位压降下的平均努塞尔数Nus表征,其表达式如下

Nus=Num/ΔP

(5)

式中,ΔP为流体压降,其表达式如下

ΔP=Pin-Pout

(6)

式中,Pin、Pout分别为流体入口压力和出口压力。

换热器的综合振动强化传热性能通过综合传热性能评估因子ζPEC表征[20],其表达式如下

(7)

式中:下标v表示振动条件下的相关参数;f为阻力系数,其表达式如下

(8)

式中,um为平均流速。

1.6 网格独立性及计算方法论证

网格独立性分析基于SSD-HCT换热器开展,如表2所示。计算采用上述计算方法,入口速度uin=0.35 m/s,对比数据选择4根HCT的平均面均传热系数hm。

表2 网格独立性分析

从表2可知,方案II的网格为“1.2 计算域和网格”所介绍的网格(参见图3),方案I和III划分策略一致,分别在方案II的基础上减小/增加单元尺寸和边界层数得到,单元数为流体域和结构域的单元数之和。

由表2可知:当单元数降低时(方案I),hm和计算耗时均降低,hm的与编号II网格计算结果的相对误差为3.93%;当单元数增加时(方案III),hm和计算耗时均升高,hm的与方案II网格计算结果的相对误差为0.46%。基于计算精度和计算效率的综合考虑,选择方案II可满足需求。

文献[21]试验测试了换热器内单管HCT的壳程努塞尔数Nu,并得到其经验公式如下

Nu=19.64Re0.513Pr0.129γ0.938

(9)

因文献[21]中HCT换热器的结构和材料与本文的一致,故计算方法论证基于文献[21]开展。本文计算方法的计算结果与经验公式结果的对比,如图5所示。

图5 计算结果与经验公式结果的对比

从图5可知,两者结果基本一致,最大误差仅为5.90%,说明本文计算方法得到的结果是可靠的。

2 结果分析

2.1 流场和温度场分析

SSD-HCT换热器和OSD-HCT换热器壳程流场的流线分布,如图6所示。其中uin=0.35 m/s。

图6 两种换热器壳程流场流线分布

从图6可知:

(1) 由于SD的导流作用,壳程流体在换热器壳程流域内螺旋流动,且OSD-HCT换热器内显示流线的流速较SSD-HCT换热器内显示流线的流速高。

(2) SSD-HCT换热器内,壳程流体纵掠HCT;OSD-HCT换热器内,壳程流体横掠HCT。从流体冲击的角度方面分析,流体横掠HCT时将会产生边界层分离现象,故OSD-HCT换热器内的HCT将会有更佳的传热性能。

两换热器壳程流场的截面温度分布云图,如图7所示。其中uin=0.35 m/s,截面为y-z面。

图7 两种换热器壳程流场的温度云图

从图7可知:两换热器内的壳程流体从入口至出口均逐渐升高,且OSD-HCT换热器内壳程流体出口温度(298.13 K)明显高于SSD-HCT换热器内壳程流体的出口温度(296.51 K),说明OSD-HCT换热器内HCT具有更好的传热性能,这与前面从流体冲击角度的分析结论一致。

基于场协同理论,当流速和温度梯度一定时,场协同角(流速和温度梯度夹角)越小,传热元件传热性能越佳。

两种类型换热器管壁附近场协同情况如图8所示。由图8可知,对于SSD-HCT换热器,SD和HCT同向螺旋,场协同角(α)接近90°,故HCT传热性能不佳,致使出口温度较低;对于OSD-HCT换热器,SD和HCT反向螺旋,迎流面的场协同角α接近0°,故HCT传热性能较佳,出口温度较高。

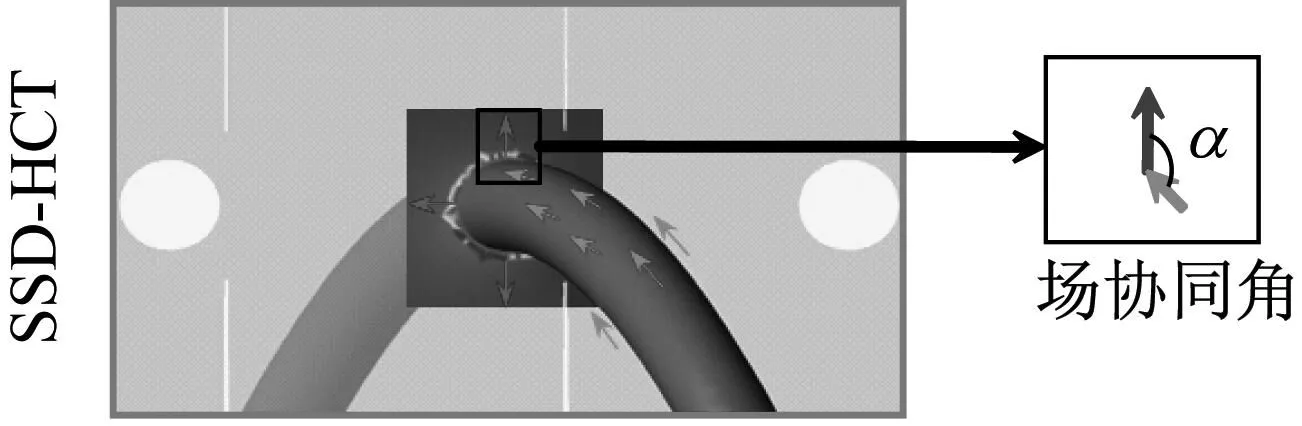
图8 两种换热器管束壁面附近的场协同角

2.2 HCT传热性能分析

SSD-HCT换热器和OSD-HCT换热器内各编号HCT在不同流速下的Nu和Nuv,如图9所示。其中,振动数据为FSI计算的结果,非振动数据为不考虑FSI时的流场计算结果。

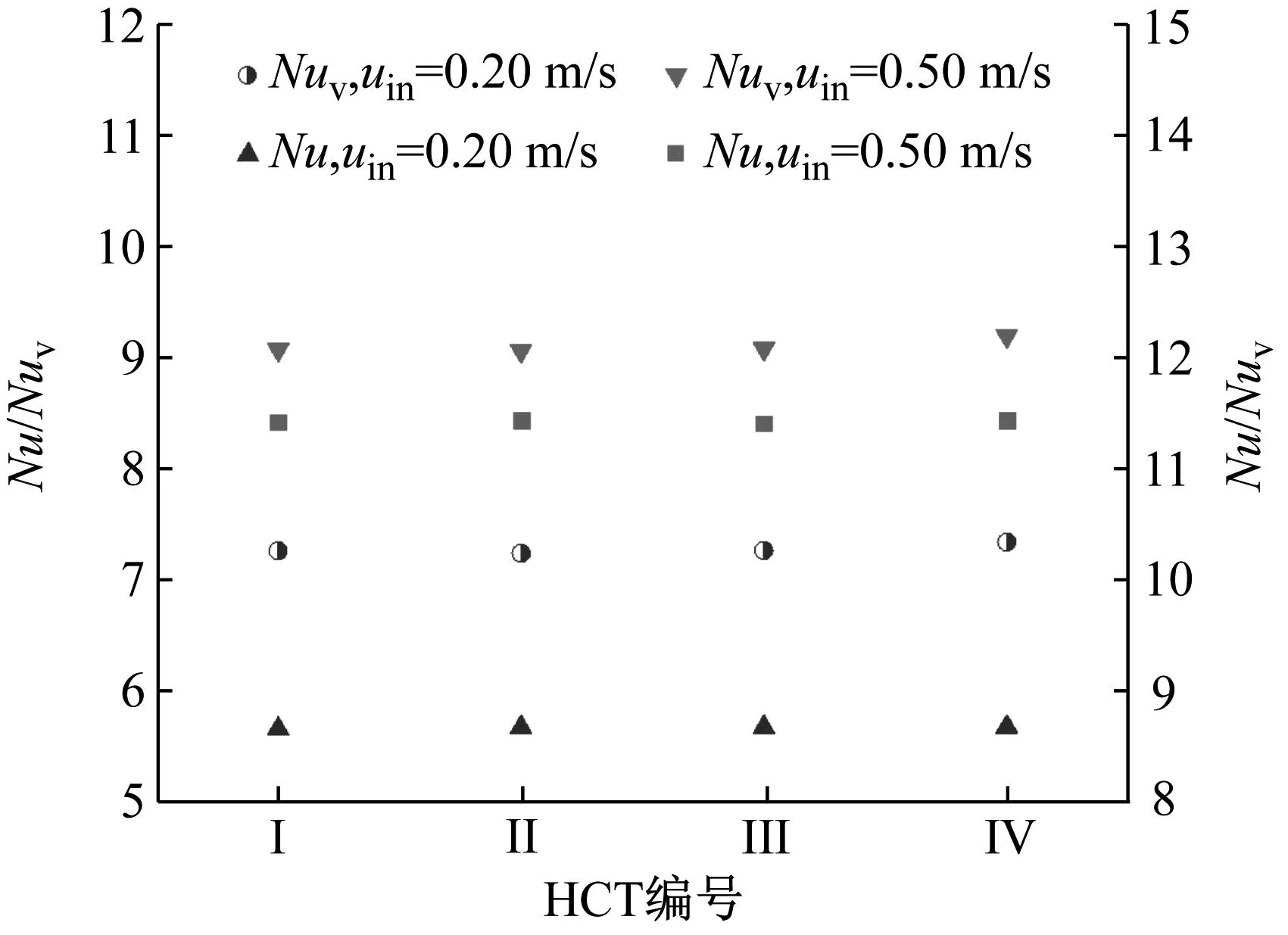
(a) SSD-HCT换热器

从图9可知:

(1) 对于不同类型的换热器,高流速(uin=0.50 m/s)下HCT的Nu和Nuv均高于低流速(uin=0.20 m/s)下HCT的Nu和Nuv,说明流速的增加有助于HCT传热性能的提高,这与文献[4,6,9]的结论一致。

(2) 不同类型的换热器和不同的流速条件下,Nuv均大于Nu,说明振动有助于HCT传热性能的提高,即实现了振动强化传热。另外,SSD-HCT换热器Nuv的增幅更大,这是因为在相同入口流速条件下SSD-HCT换热器中的HCT在流体诱导下的振动强度更大所致,如表3所示。

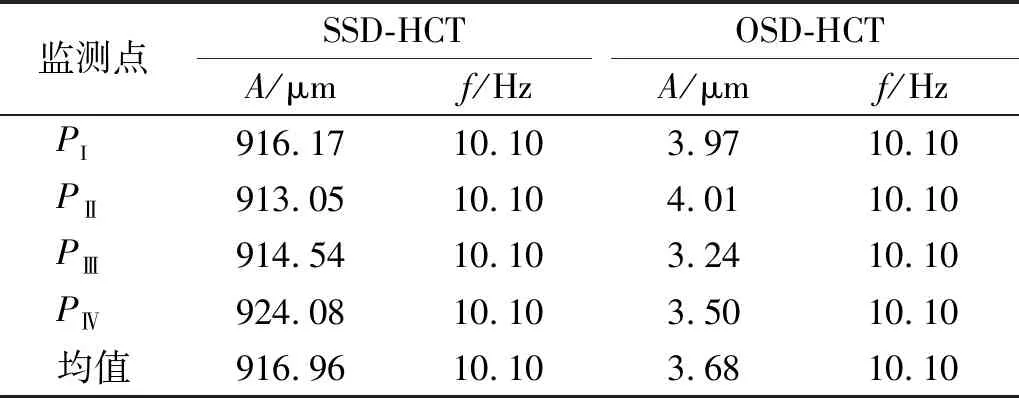
表3 监测点的振幅和频率(uin=0.20 m/s)

(3) OSD-HCT换热器内HCT的Nuv和Nu均大于SSD-HCT换热器内HCT的Nuv和Nu,说明SD和HCT反旋向布置时,换热器内HCT的传热性能较好。这是由于SSD-HCT换热器内壳程流体纵掠HCT,而OSD-HCT换热器内壳程流体横掠HCT所致,这也与前面从流体冲击角度分析的结论一致。

为进一步分析SD旋向对HCT传热性能的影响,基于两种类型的换热器,对不同uin时振动条件下的Num进行了计算,如图10所示。

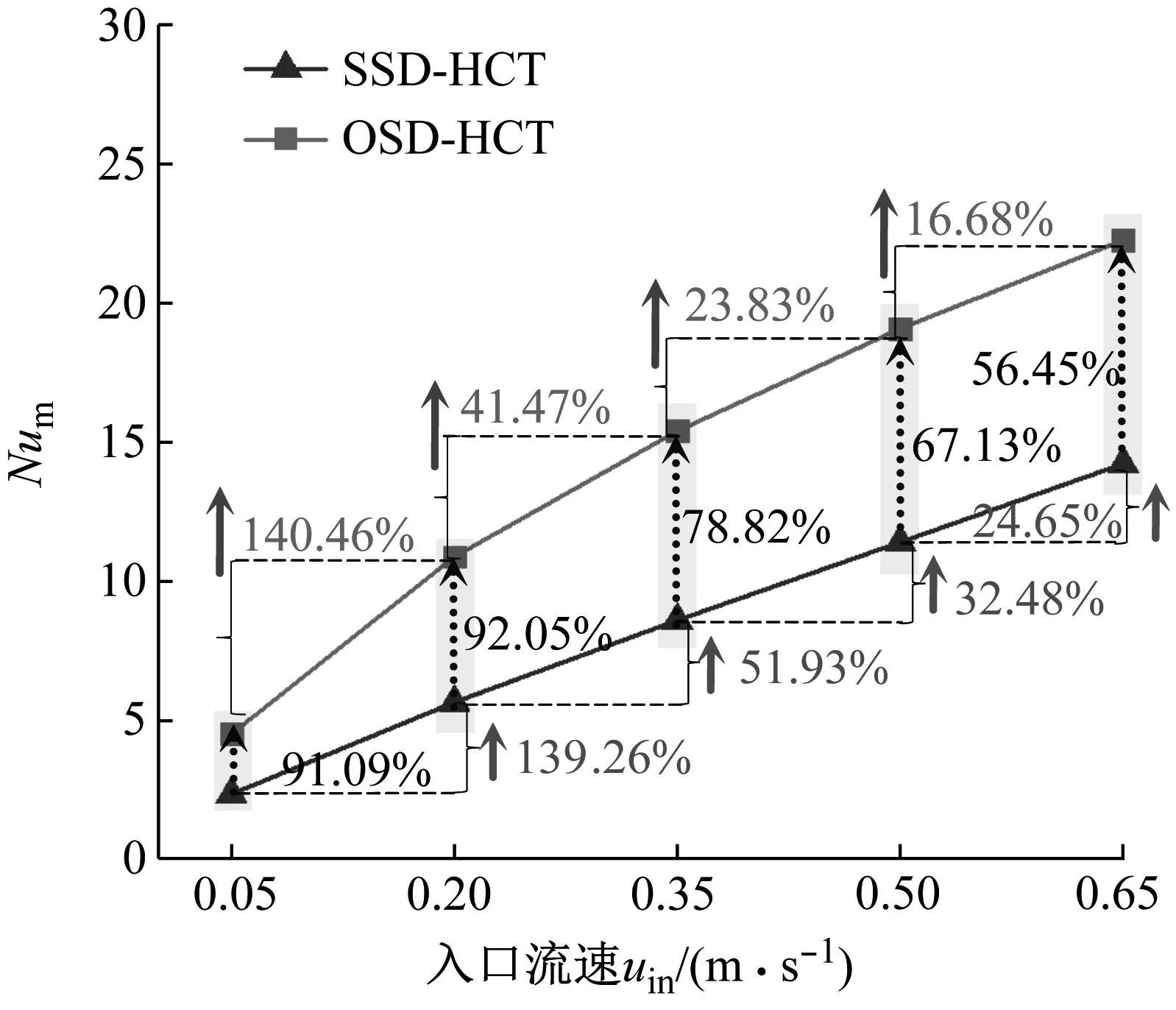
图10 两种换热器内Num随uin的变化

从图10可知:

(1) 两种类型换热器内HCT的Num均随uin的增加而增加,且增幅随uin的增加逐渐降低。

(2) 不同uin条件下,OSD-HCT换热器内HCT的Num均高于SSD-HCT换热器内HCT的Num,且在本文计算参数范围内的最小增幅为56.45%。这也进一步说明了SD和HCT反旋向布置时换热器内HCT的传热性能较好。

2.3 换热器单位压降传热性能分析

SD旋向或uin的改变会不可避免地导致流动阻力的变化,两种类型换热器在不同uin下的压降变化,如表4所示。此处仅对非振动条件下的压降进行分析。

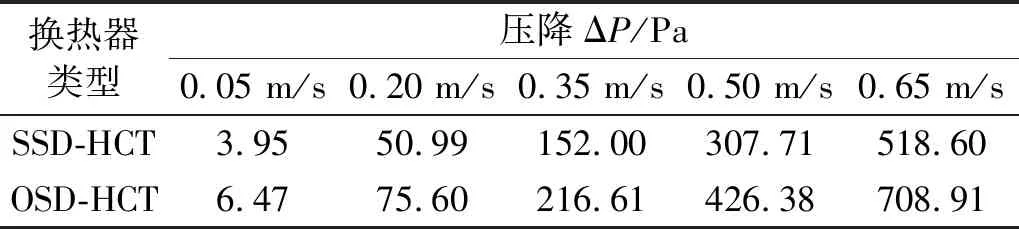
表4 两种换热器在不同流速下的压降对比

从表4可知:

(1) 对于不同类型的换热器,ΔP均随uin的增加而增加,说明当uin增加时,壳程流体的流动阻力增大。

(2) 当uin一定时,OSD-HCT换热器内的ΔP均高于SSD-HCT换热器内的ΔP,说明当SD和HCT反旋向布置时壳程流体的流动阻力较大。

从上面的分析可知,当SD和HCT反旋向布置时,换热器内的HCT具有较好的传热性能,但壳程流体的流动阻力较大。

据此,为评判换热器单位压降的传热性能,对非振动条件下两种类型的换热器在不同uin下的Nus进行了计算,如表5所示。

表5 两种换热器在不同流速下的Nus对比

从表5可知:

(1) 对于不同类型的换热器,Nus均随uin的增加而降低,说明当uin增加时,换热器单位压降下的传热性能降低。

(2) 当uin一定时,OSD-HCT换热器内的Nus均高于SSD-HCT换热器内的Nus,说明当SD和HCT反旋向布置时换热器单位压降下的传热性能较好,这进一步说明了OSD-HCT换热器的优势。

2.4 换热器综合振动强化传热性能分析

基于图9的分析,振动有助于HCT传热性能的提高,但这种单纯对Nu的分析具有很大的局限性,其同样忽略了流动阻力的影响。据此,为评判换热器的综合振动强化传热性能,需基于ζPEC进行综合评判。

两种类型换热器在不同uin条件下的ζPEC对比情况,如图11所示。其中,uin=0.20 m/s、0.35 m/s和0.50 m/s。

图11 两种换热器的ζPEC对比

从图11可知:

(1) 各种条件下ζPEC的计算结果均大于1,说明两种类型的换热器在不同条件下均实现了振动强化传热。然而,同一uin条件下SSD-HCT换热器的ζPEC明显高于OSD-HCT换热器的ζPEC,这说明SSD-HCT换热器内HCT的振动强化传热效果明显较高。

(2) 对于不同类型的换热器,ζPEC均随uin的增加而降低,且降幅逐渐减低,其中SSD-HCT换热器的ζPEC受uin的影响更明显,当流速增高时两者的综合振动强化传热性能逐渐接近。这说明,当uin增加时换热器的综合振动强化传热能力逐渐降低。

结合前面对流场、场协同和单位压降的传热性能分析,可知:当SD和HCT同旋向布置时,场协同角较大,HCT的传热能力较低,但其振动强化传热的能力较高;反之,当SD和HCT反旋向布置时,场协同角较小,HCT的传热能力较高,但其振动强化传热的能力较低。需要说明的是,这些结论尚未在公开发表的文献中发现。

结合上述研究结论,要想获得具有更高综合传热能力SSD-HCT换热器,可充分利用流体诱导的振动实现HCT的强化传热,但要付出管束疲劳寿命降低的代价;而对于OSD-HCT换热器,避免或减低流体诱导的振动即可获得具有较高综合传热性能的换热设备,同时延长设备的使用寿命,这具有重要的工程价值。理论研究方面,可结合本文的研究结论把传统振动强化传热理论与场协同理论进行有机结合,为场协同理论的深入研究提供依据,进而有望开展流向-振动-场协同理论方面的耦合探究。