管束结构流弹失稳的数值预测方法研究
2023-12-18冯志鹏蔡逢春臧峰刚齐欢欢
冯志鹏, 蔡逢春, 臧峰刚, 齐欢欢, 黄 旋, 刘 帅
(中国核动力研究设计院 核反应堆系统设计技术重点实验室,成都 610213)
蒸汽发生器是核岛内的关键设备之一,传热管束是其核心部件,容易发生流致振动问题。在已发现的流致振动机理中,流弹失稳(流体弹性不稳定性)能在短时间内造成结构损坏,在工程设计中必须避免发生这种现象。
目前,工程中采用基于准静态理论得出的Connors公式计算临界流速[1]
(1)
式中:K为Connors系数;fi、ζi、D、m分别为传热管的第i阶频率、第i阶模态阻尼比、外径、单位长度质量;ρ为流体密度;无量纲量2πζim/ρD2称为质量阻尼参数(mass damping parameters,MDP)。随着对流弹失稳研究的深入,人们发现Connors公式较难描述流弹失稳机理,而其他理论模型,如准稳态模型、非稳态模型和流管模型,由于需要大量试验参数,制约了工程应用与推广。
在没有经验数据的情况下详细描述流动的最佳途经是采用计算流体力学(computational fluid dynamics,CFD),但考虑到真实管束结构及其众多可能的排列形状,使得仿真计算量大[2],时间成本高,目前这种方法仅限于非常简单几何结构的数值模拟。一种更实用的方法是利用CFD来预测可以集成到理论模型中的参数,如Meskell等[3]利用数值模型估算了正三角形管束的稳态流体力,然后将这些力参数与准稳态模型结合使用;Hassan等[4]利用CFD来模拟非稳态流体力和由管道运动产生的相应力系数,并与非稳态模型结合使用;赵燮霖等[5]采用CFD获取半解析模型中的相位延迟函数,预测了横向流作用下间距比为1.375的平行三角形与正三角形管束结构的流弹失稳阈值。然而,目前还没有一个全面的数值研究来预测这些流弹失稳理论模型中的全套流体力相关参数,也缺乏对这些理论模型的对比研究。
因此,本文采用理论建模和CFD计算相结合的方式,推导出准稳态模型、非稳态模型和流管模型的动力学方程,发展理论模型中众多参数的辨识方法,开展管束结构流弹失稳的数值预测,最终确定临界流速、对比分析各预测模型,为蒸汽发生器的流致振动分析与设计提供技术支撑。
1 动力学方程
压水堆核电站采用立式自然循环式蒸汽发生器,直立式倒U形传热管束是其核心部件,图 1为U形弯管段的结构和流场示意图。本文的研究对象为华龙一号的ZH65型蒸汽发生器的管束,主要几何参数如表1所示。
考虑由N根管组成的管束,将管束中的管子看成多跨梁结构,利用梁的振动理论,第i根管在x向和y向的运动方程可写成
(2)
式中:EI为弯曲刚度;z为管子轴向坐标;m为单位管长质量;c为结构阻尼系数;g和h分别为x向和y向的流体弹性力;下标i为第i根管。
根据式(2)中流体弹性力的选取,将形成不同的流弹失稳理论模型。首先通过理论推导,全面建立起目前研究最广泛的三种流弹失稳理论模型的控制方程和关键参数的数学模型,以开展流体力相关参数辨识和数值预测方法建立。
1.1 准稳态模型

(3)

横流作用下的管束的运动方程可写为
(4)
(5)
式中:[I2]、[A]、[B]、[K]分别为单位矩阵、附加质量矩阵、流体阻尼矩阵、流体刚度矩阵;t为时间;ω为圆频率;δ为对数衰减率;a=U/U∞。
1.2 非稳态模型
在非稳态理论中[7],作用在第i根管上的非稳态流体力取决于管子自身及相邻管子在流场中的位移、速度和加速度,表示为
式中:下标i、j为第j根管运动对第i根管所受流体力的影响;α、σ、τ、β的各种形式为流体力相关系数;R为管半径;Ug为管束的间隙流速,其它变量与前文相同。

得到流体力后,与振动方程联立,管束的动力学方程可表示为
(8)
式中:[Ms]、[Cs]、[Ks]为管的质量矩阵、阻尼矩阵和刚度矩阵;[Ma]、[Ca]、[Ka]为流体的附加质量矩阵、附加阻尼矩阵和附加刚度矩阵;z={x,y}′。
1.3 流管模型
流管模型基于一维非稳态流动理论,用曲线坐标s表示流动路径,瞬时流管面积、速度和压力分解为平均项和波动项
A(s,t)=A0+a(s,t)
(9)
U(s,t)=U0+u(s,t),P(s,t)=P0+p(s,t)
(10)
采用相位滞后函数φ(s)来考虑扰动延迟效应,面积扰动函数a(s,t)表示为
a(s,t)=a(sm,t)f(s)eiφ(s)
(11)
式中:a(sm,t)为最小间隙位置的面积扰动;f(s)为人工衰减函数。
不可压缩流体的连续性方程为
(12)
式中:U(s,t)为流体速度向量;n(s)为垂直于控制体表面的单位向量。
将式(9)和式(10)代入式(12),假设扰动是频率为ω的谐波,从入口s=si到出口s=se沿曲线坐标s积分,消除稳态项和高阶项,并无量纲化
(13)
采用类似推导过程,可得到控制体的动量方程
(14)

(15)
得到流体力后,与振动方程联立,即可建立基于流管模型的动力学方程
(16)

理论上,流管模型可以不需要任何试验数据,但在实际使用过程中,模型中许多参数来自于定性的流动可视化和假定,缺乏合理的定量表征方式,本文利用数值方法来确定流管模型中的两个关键参数:流管边界和相位滞后。
2 流体力参数辨识
本文将理论模型与CFD计算相结合,通过仿真数据驱动的方式,发展计算这些参数的辨识方法,进而建立预测管束流弹失稳行为的数值预测方法。
2.1 CFD模型
管束及计算域和局部网格示意图,如图4所示。其中,上下两侧为半管,出口在最后一行管的间隙处截断;入口区域设置为速度入口(U∞),出口区域设为inletOutlet条件,振动管设置为运动壁面,流场上下两侧和其它管表面为固定无滑移壁面;管束周围边界层数量为15层,周向尺寸为0.01D,第一个网格距管束壁面为0.1%D,以保证y+≤1,使用1.01的扩展系数从边界层单元过渡到四面体单元。流场模拟基于开源CFD工具OpenFOAM,湍流模拟采用SST模型。文献[8]详细介绍了数值模型,本文不再赘述。
为了定量描述数值预测结果与实验结果的相对误差情况,定义相对均方根误差RMSE
(17)
式中:xi为计算值;yi为试验值;N为样本数目。
2.2 准稳态模型的流体力参数辨识


2.3 非稳态模型的流体力参数辨识
对于非稳态模型,以图4中1根管在升力和阻力方向上作强迫振荡,其余管固定,来计算作用在各管上的流体力等信号。
计算的升力系数幅值和相位差与文献中的试验结果比较,如图6所示[9]。计算的流体阻尼、流体刚度与文献中的试验结果比较[10],如图7所示。从图7可知,数值预测结果基本上反映了流体力系数的变化情况,预测结果与试验数据吻合较好,升力系数幅值的相对均方根误差为88%,在Ur=10处的误差较大;相位差的相对均方根误差为12.99%。采用相同的方式,可得到所有其它流体力参数。
2.4 流管模型的流体力参数辨识
联合图像处理技术和CFD流场计算,开发了流管特征提取程序,识别的流管边界如图8所示。然后在识别出的流管边界中心线上布置监测点,采集这些监测点的速度时程,利用互相关函数法,计算出管运动和由此产生的流动扰动之间相位滞后。计算得到的相位滞后与试验数据[11]的比较,如图9所示。从图9可知,本文建立的数值预测方法可以很好地预测相位滞后,相对均方根误差为35%。
3 临界流速预测
利用CFD计算可以辨识不同输入参数的优势,在成功获得准稳态模型、非稳态模型、流管模型中的全套流体力相关参数的基础上,建立管束结构流弹失稳的数值预测方法,最终确定临界流速,并对比研究三种理论模型的预测效果。
在工程中,流体密度、横向流速沿传热管分布并不均匀,需要计算相应的等效值,等效流速定义为
(18)
等效质量和等效密度定义为
(19)
(20)

根据工程经验,选取由4根防振条支承且弯曲半径最大的传热管进行分析。将振型函数和热工水力条件(横向速度分布、流体密度分布)代入式(18)~式(20),其中管子的振型函数通过有限元方法得到,传热管有限元模型示意图如图10所示。传热管的典型振型图如图11所示。

图1 蒸汽发生器U形弯管段的结构和流场示意图
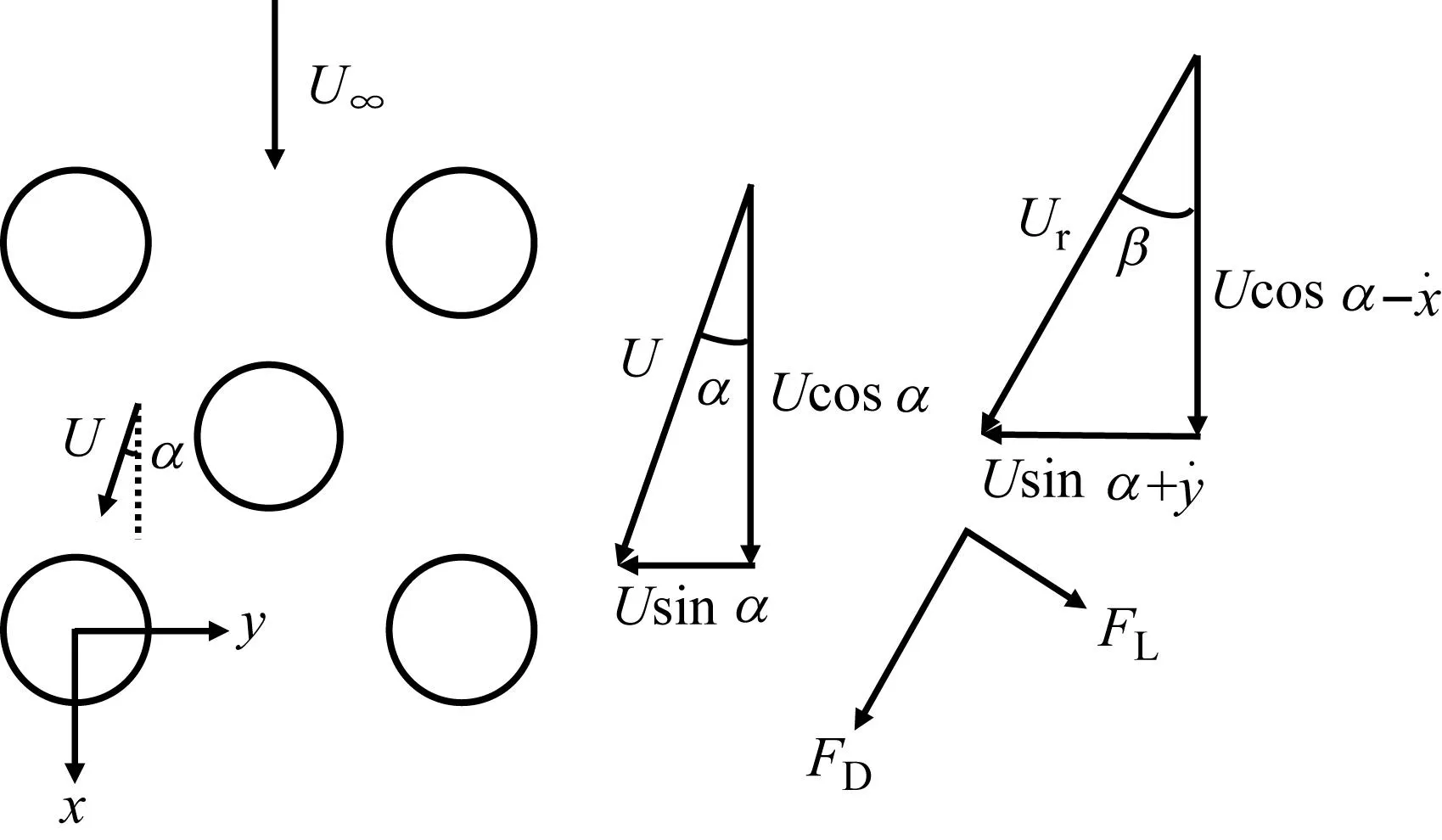
图2 作用于振动管的合速度

图3 作用于振动管的流体力

图4 计算域和局部网格细节
图5 升力系数的空间变化

图6 升力系数的幅值和相位差与试验数据的比较

图8 流管边界提取

图9 相位滞后预测结果

图10 有限元模型

图11 典型振型
利用本文建立的数值预测方法计算得到的稳定性图如图12所示。并与文献试验结果[12]、工程验证性试验结果以及现有工程方法的结果进行对比。其中,工程验证性试验和工程方法均基于Connors公式,工程方法的结果采用自主研发的专用软件计算获得。选取了几阶典型模态对应的不稳定比如表2所示。从表2可知,准稳态理论计算的结果接近线性,且预测误差较大;非定常模型与流管模型的计算结果相近,与试验结果吻合较好;现有工程方法给出的结果最保守;对于所有的模态,流弹不稳定的裕量都是足够的,工程算例的管束不会发生流弹失稳,与工程验证性试验的结论一致。
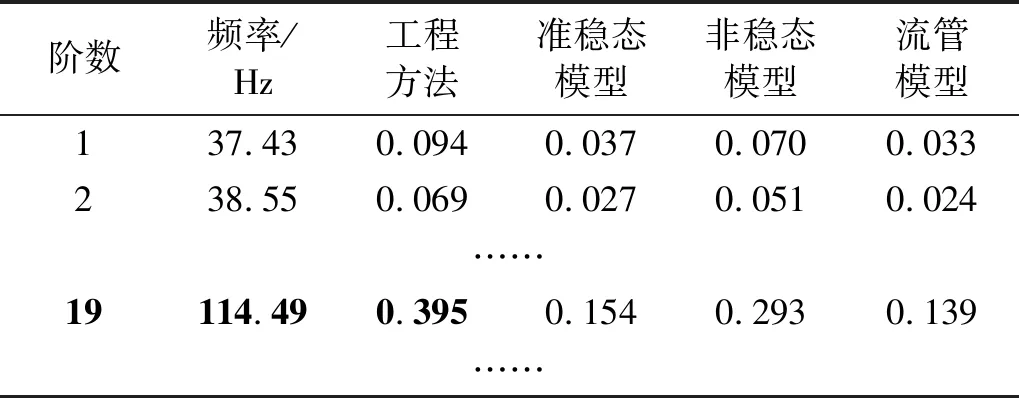
表2 各阶模态对应的流弹不稳定比
4 结 论
本文采用理论建模和CFD计算相结合的方式,发展适用于工程的管束结构流弹失稳预测的数值方法,得到以下结论:
(1) 形成了通过CFD计算流体力相关参数的辨识方法,提出了结合图像处理技术提取流管特征的定量表征技术,通过仿真数据驱动的方式,获得了全套流体力相关参数。
(2) 基于流弹失稳的三种理论模型,建立了数值预测方法,完成了工程应用和对比研究,并用试验数据进行了验证,CFD计算与理论模型耦合的数值预测方法,具备一定的实用性。
(3) 数值预测方法结合了理论建模的严谨性和CFD计算可考虑实际结构动力学特征的优点,又避免了复杂管束流固耦合模拟对海量计算资源的需求,降低了理论模型对试验数据的依赖,有利于在工程中推广应用。
