分层多尺度决策信息系统的序贯三支决策
2023-12-17李磊军米据生李美争
刘 芳 ,李磊军,2* ,米据生,2 ,李美争
(1.河北师范大学数学科学学院,石家庄,050024;2.河北省计算数学与应用重点实验室,石家庄,050024;3.河北师范大学计算机与网络空间安全学院,石家庄,050024)
1982 年Pawlak[1]提出能有效处理不精确、不确定信息的粗糙集理论,2007 年Yao[2]提出概率粗糙集模型,又提出决策理论粗糙集模型[3].基于决策理论粗糙集模型,Yao[4]提出三支决策模型.三支决策将整个论域划分为三个互不相交的区域:正域、负域、边界域;对每个区域制定不同的行动方案:接受、拒绝、延迟决策.三支决策与传统的二支决策相比,在接受和拒绝两种决策之外给出第三种选择,即延迟决策,避免直接接受或者拒绝带来的风险.该模型符合人类的思想与认知习惯,适用于解决不确定性决策问题.此后,三支决策的研究受到广泛关注.Huang et al[5]提出带有序关系的三支决策方法,Jia and Liu[6]在多准则环境下进行三支决策,Zhang et al[7]在证据理论的基础上研究三支决策模型.2013 年Yao[8]提出序贯三支决策模型,有关序贯三支决策的研究也成为热门话题.Xu et al[9]给出三种序贯三支决策模型.Qian et al[10]提出一种基于序贯三支决策的属性约简方法.Zhang et al[11]基于最优化的思想,设计惩罚函数来优化成本参数,提升了序贯三支决策的分类精度.Li et al[12]构建代价敏感序贯三支决策模型.Qian et al[13]提出基于多粒度的序贯三支决策的广义模型,实现了五种多粒度序贯三支决策,还将序贯三支决策与层次粗糙集模型相结合,提出一种新的序贯三支决策模型[14].
实际生活中经常需要在多尺度的环境下对同一对象进行观察、分析和决策.2011 年Wu and Leung[15]提出多尺度信息系统的概念,又称为Wu-Leung 模型,系统中每个对象在每个属性下有不同的属性值,并存在从细尺度到粗尺度的粒度转换.之后,Wu and Leung[16]进一步研究了多尺度信息系统中最优尺度选择问题.Zheng et al[17]基于证据理论讨论了多尺度有序决策系统的最优尺度选择.Chen et al[18]将研究背景放到多尺度集值信息系统中,展开系列讨论.因为数据集上不同属性可能具有不同的尺度数目,Li and Hu{19}提出广义多尺度信息系统,引入尺度组合的概念,提出广义多尺度信息系统的知识获取模型.众多学者对广义多尺度信息系统展开了广泛研究,取得了重要进展[19-21].
将多尺度信息系统与三支决策相结合是值得研究的问题.Deng et al[22]提出多尺度决策信息系统中多属性决策的三支决策方法.Hao et al[23]基于三支决策的思想,在多尺度决策信息系统中构建序贯三支决策模型,并基于该模型在动态变化的多尺度决策信息系统中选择最优尺度.Luo et al[24]研究了不完备多尺度信息系统上的序贯三支决策问题.Cheng et al[25]提出多尺度决策信息表中基于序贯三支决策的最优尺度选择和属性约简方法.
本文基于多尺度决策信息系统讨论序贯三支决策问题.首先,对多尺度决策信息系统进行分层,得到从粗尺度到细尺度的多个单尺度决策信息系统.在每个单尺度决策信息系统上讨论属性子集序列选择问题,构建粒度层面上的序贯三支决策模型.依次考虑从粗尺度到细尺度的每个单尺度决策信息系统,构建尺度层面上的序贯三支决策模型,最终得到分层多尺度决策信息系统的序贯三支决策模型,有效处理多尺度决策信息系统的分类问题.
1 相关理论
本节介绍决策理论粗糙集、相对损失函数和多尺度决策信息系统等基本概念.
1.1 决策理论粗糙集设U是一个非空集合,称为论域,E⊆U×U是U上的等价关系,二元组(U,E)称为Pawlak 近似空间.根据等价关系E,可将U划分为不相交的集合,记作U/E=
在Pawlak 粗糙集的基础上,Yao[2]提出了概率粗糙集模型.
定义1[2]设U为论域,E是U上的等价关系.∀x∈U,x在等价关系E下的等价类为[x]E.∀D⊆U,概率下、上近似定义如下:
其中,0 ≤β<α≤1,且条件概率为:
该条件概率表示可以将x划分到集合D中的概率,其中,| |代表集合的基数.
给定一组阈值(α,β),0 ≤β<α≤1,通过容忍一定的错误分类率来提高分类效率.根据阈值,可将全部对象划分到正域、边界域、负域三个互不相交的区域:
Yao[3]借助贝叶斯最小风险准则理论,提出决策理论粗糙集模型,给出概率粗糙集中阈值和三个区域的语义解释.
假设状态集合为Δ={D,¬D},D和¬D分别表示对象属于集合D和对象属于集合D的补集.假设行动集合为A={aP,aB,aN},aP,aB,aN分别代表接受、延迟决策和拒绝,即将对象划分到集合D的正域、边界域和负域.
对每一个备选对象采取不同的分类行动都有相应的成本或损失,如表1 所示.其中,λPP,λBP,λNP表示将属于D的对象分类到D的正域、边界域、负域的损失函数,λPN,λBN,λNN表示将不属于D的对象分类到D的正域、边界域、负域的损失函数.基于合理的假设,损失函数大小满足λPP≤λBP≤λNP,λNN≤λBN≤λPN.

表1 损失函数Table 1 The loss function
基于损失函数和条件概率,可计算对对象x采取不同行动的期望损失,具体计算如下:
由贝叶斯最小风险准则,根据期望损失函数的关系来制定分类规则:
容易得到:
于是,上述规则可以简化为:
其中,阈值的计算如下:
若损失函数满足:
1.2 相对损失函数由阈值的计算公式可以看出,阈值大小与损失函数的值相关,并且只与损失函数之间的差有关.由此,Jia and Liu[6]提出相对损失函数的概念.令λPP,λBP,λNP同时减去λPP,λPN,λBN,λNN同时减去λNN,得到相对损失函数如表2 所示.表2 中的相对损失函数值仍满足关系

表2 相对损失函数Table 2 The relative loss function
一个信息系统中,每个对象在每个属性下由属性值导出的相对损失函数如表3 所示(为了讨论方便,假设下文讨论的属性均为效益型属性,即属性值越大越好).其中,σ为引入的参数,σ∈[0,0.5];xij表示对象xi在属性aj下的取值;maxj为属性aj的值域中的最大值,minj为属性aj的值域中的最小值.

表3 由属性值导出的相对损失函数Table 3 The relative loss function derived from attribute values
由相对损失函数导出的阈值的计算如下:
定理1[6]∀xij∈(minj,maxj),有:
(1)αij随σ的增大而减小;
(2)βij随σ的增大而增大;
(3)γij与σ的变化无关.
定理2[6]∀xij∈(minj,maxj),有:
(1)POS(D)区域随σ的增大而增加;
(2)BND(D)区域随σ的增大而减小;
(3)NEG(D)区域随σ的增大而增加.
1.3 多尺度决策信息系统
定义3[18]S=(U,A∪{d},V,F)是一个多尺度决策信息系统,其中d∉A,d:U→Vd是单尺度决策属性,Vd是决策属性d的值域.
下文假设所有条件属性具有相同数量的K个尺度.于是多尺度决策信息系统可以表示为:
将多尺度决策信息系统S分层,得到K个单尺度决策信息系统.对任意h∈{1,2,…,K},第h个单尺度决策信息系统表示为Sh=(U,Ah∪{d},Vh,Fh).其中,U是论域;Ah={|j=1,2,…,m};d是决策属性;是值域;Fh:U→Vh是特征函数.
定义4[18]S是一个多尺度决策信息系统,Sh为第h个单尺度决策信息系统.Sh上的等价关系定义为:
∀x∈U,x在Eh下的等价类表示为:
得到U的一个划分:
2 分层多尺度决策信息系统的序贯三支决策模型
将多尺度决策信息系统分层可得多个单尺度决策信息系统,由粗尺度到细尺度依次讨论.多尺度决策信息系统的序贯三支决策过程如图1 所示,在每个单尺度决策信息系统中进行序贯三支决策须有构建序贯三支决策模型的粒度结构.

图1 多尺度决策信息系统S 上的序贯三支决策过程Fig.1 Sequential three-way decision process on multi-scale decision information system S
2.1 粒度结构的构造从两个不同的视角,提供两种选择属性子集序列的方法,得到具有包含关系的、属性个数逐渐增多的属性子集序列,由此构造两种粒度结构.
2.1.1 基于聚类分析的属性子集序列选择首先定义条件属性之间的距离,再利用聚类分析方法对条件属性进行聚类,最后利用聚类结果得到条件属性子集序列.
令S=(U,A∪{d})是一个信息系统,如表4所示,其中U={x1,x2,…,xn}为论域,A={a1,a2,…,am}为条件属性集合,{d}为决策属性.为了刻画属性之间的距离,将表4 中的信息转化为表5 的形式,其中,[xi]j为对象xi(1 ≤i≤n)在属性aj(1 ≤j≤m)诱导的等价关系下的等价类.

表4 信息系统表Table 4 Information system table

表5 用等价类刻画距离Table 5 Characterizing distance by equivalence classes
Chen et al[26]定义了两个粒之间的距离和粒结构之间的距离.设s=(x),t=(y)是两个粒,则s和t之间的距离定义为:
是两个粒结构,则,之间的距离定义为:
利用上述两个距离的定义,得到定义5.
定义5S=(U,A∪{d})是一个信息系统,∀ap,aq∈A,两个属性ap,aq之间的距离定义为:
根据定义5 得到属性两两之间的距离,如表6所示,其中,dij=d(ai,aj)(1 ≤i,j≤m),然后利用系统聚类法,选择适当的聚类数目k,完成聚类.记聚类结果为A={G1,G2,…,Gk},认为Gi(1 ≤i≤k)中的属性在对论域进行划分时的作用是相似的,因此选取其中一个属性后可将Gi中的其他属性看作冗余属性.

表6 属性之间的距离Table 6 The distance between attributes
记属性子集Gi中选取的属性为ci,得到属性子集序列{c1}⊂{c1,c2}⊂…⊂{c1,c2,…,ck}.
例1S=(U,A∪{d})是一个信息系统,如表7(其中数据来自文献[27])所示.基于表8 中属性之间的距离,采用系统聚类法中的最大距离法进行聚类(k=4),从而对条件属性a1,a2,…,a6进行聚类分析,聚类结果如表9 所示.

表7 信息系统STable 7 Information system S

表8 信息系统S 中属性之间的距离Table 8 The distance between attributes in information system S

表9 聚类结果Table 9 The clustering results
分别从每个类别中选取一个属性,从G1中选取的属性记为c1=a3,从G2中选取的属性记为c2=a6,从G3中选取的属性记为c3=a4,从G4中选取的属性记为c4=a1,得到属性子集序列为{a3}⊂{a3,a6}⊂{a3,a6,a4}⊂{a3,a6,a4,a1}.
2.1.2 基于属性依赖度的属性子集序列选择首先描述基于边界域的属性相对依赖度,根据属性相对依赖度的大小逐个添加属性,构建具有包含关系的属性子集序列.
定义1 中,α=1,β=0 时,概率下、上近似算子退化为经典下、上近似算子.等价关系E为由属性集合B诱导出的等价关系时,记为EB.
S=(U,A∪{d})是一个信息系统,U关于{d}的决策划分为πD={D1,D2,…,Dr}.对于B⊆A,集合Di∈πD关于属性子集B的下、上近似为:
决策属性{d}相对于属性子集B的正域、边界域、负域为:
定义6[28]在信息系统S=(U,A∪{d})上决策属性{d}相对于属性子集B的依赖度定义为:
对于属性a∉B,属性a关于属性子集B的相对属性依赖度定义为:
为了构建属性子集序列,逐个添加属性得到属性子集B.借鉴启发式属性约简算法的思想,优先选择相对属性依赖度大的属性进入集合B中,直到满足ωB(πD)=ωA(πD).
基于相对属性依赖度添加属性的步骤如下:
Step 1.初始集合B=∅;
Step 2.从A-B中选择最大相对属性依赖度的属性a0,并更新集合B=B∪{a0};
Step 3.若ωB(πD)=ωA(πD),过程结束,否则,转Step 4;
Step 4.重复Step 2.
上述步骤中,集合B中的属性是逐个添加的,添加的标准为相对属性依赖度最大的属性,利用集合B中属性添加的顺序来构建属性子集序列.
信息系统为S=(U,A∪{d}),由上述过程得到的属性子集为B,记B={c1,c2,…,c|B|}.B中的属性按照添加进B的顺序排序.可以得到属性子集序列{c1}⊂{c1,c2}⊂…⊂{c1,c2,…,c|B|}.
例2仍利用表7 中的信息系统S=(U,A∪{d})进行讨论,ωA(πD)=0.25.得到属性子集B的过程如下所示:
由上述结果,可以得到属性子集序列:
设由上述两种方法得到的属性子集序列统一记为A1⊂A2⊂…⊂Aq⊆A,由A1,A2,…,Aq诱导的等价关系记为E1,E2,…,Eq.将S上的q级粒度结构记为SGj=(S,Aj,Ej),j=1,2,…,q.
2.2 序贯三支决策模型的构建令S=(U,A∪{d},V,F)是一个多尺度决策信息系统,Ω=U/{d}={D,¬D}为S中的状态集合,D和¬D分别表示对象属于集合D和对象属于集合D的补集.将S分层得到K个单尺度决策信息系统,记为Sh=(Uh,Ah∪{d},Vh,Fh),h=1,2,…,K.
设SK为最粗尺度的单尺度决策信息系统,S1为最细尺度的单尺度决策信息系统,按照从SK到S1的顺序进行序贯三支决策.从SK-1开始,每个单尺度决策信息系统的论域为上一个单尺度决策信息系统的边界域,论域不断减少并更新,记Uh为第h个单尺度决策信息系统Sh的论域,UK=U.假设Sh中的状态集合表示为Ωh=Uh/{d}={Dh,¬Dh},Dh和¬Dh分别表示对象属于集合Dh和对象属于集合Dh的补集.Ωh不断减少并更新,ΩK=Ω.
在Sh上进行序贯三支决策,Sh的结构如式(14)所示;Sh上的属性子集序列诱导出q级粒度结构,Sh在不同粒度下的结构如式(15)所示.
定义9给定一个单尺度决策信息系统Sh,阈值参数向量为(αh,βh).进行q次序贯三支决策后,关于决策类Dh的三个(αh,βh)-概率区域定义为:
上述定义描述了单尺度决策信息系统上由粗粒度到细粒度的序贯策略.第h个单尺度决策信息系统Sh上的序贯三支决策过程如图2 所示.
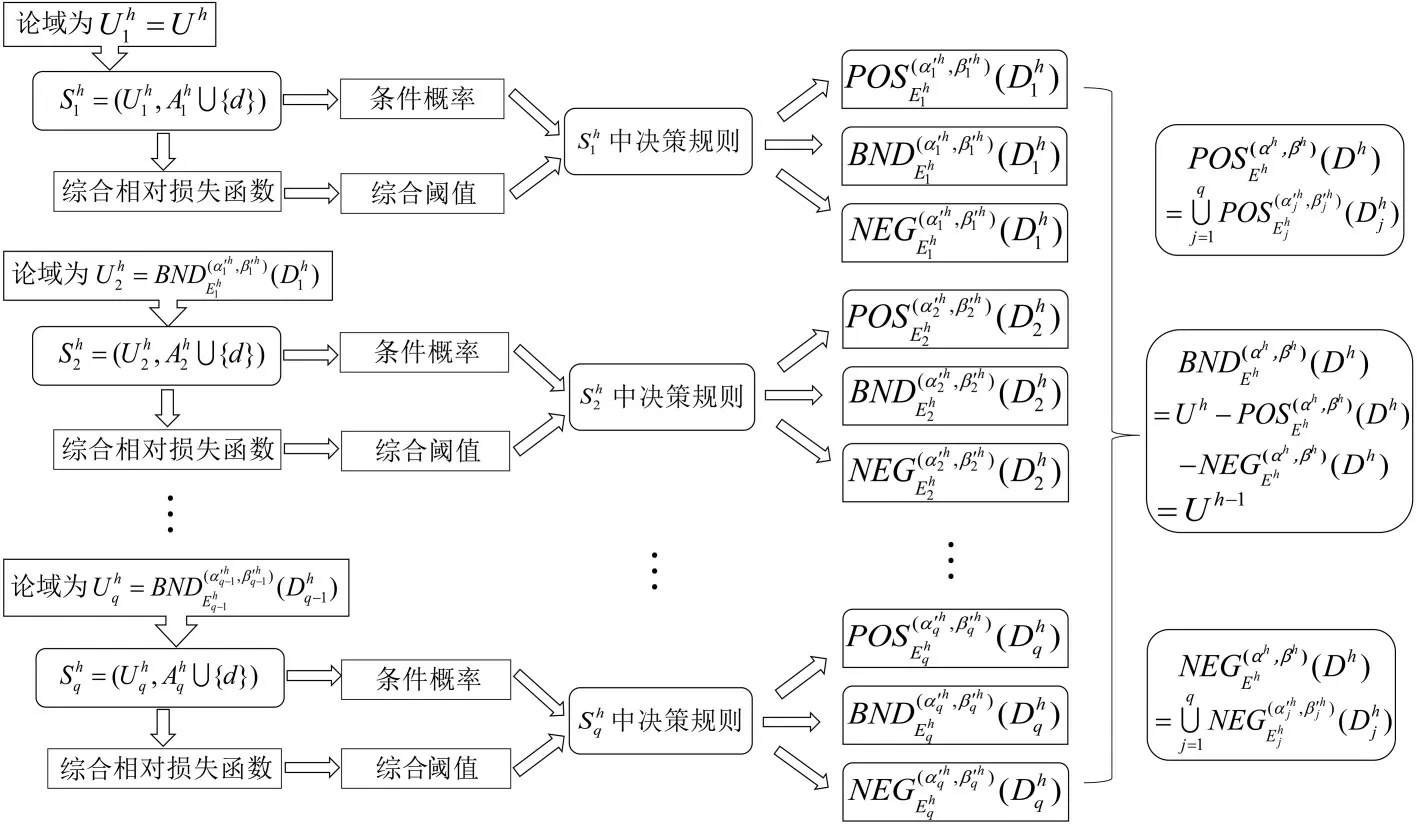
图2 单尺度决策信息系统Sh 上的序贯三支决策过程Fig.2 Sequential three-way decision process on single scale decision information system Sh
定义10第h个单尺度决策信息系统Sh经q个粒度的三支决策,最终的边界域被认为是第h-1 个单尺度决策信息系统Sh-1中的论域Uh-1.Sh-1进行q个粒度的序贯三支决策后,记POSSh-1,NEGSh-1,BNDSh-1为目前得到的全部三个概率区域,具体形式如下:
定义10 描述了从第h个单尺度决策信息系统到第h-1 个单尺度决策信息系统的序贯过程,结合定义7~9,称此模型为分层多尺度决策信息系统的序贯三支决策模型.第K个单尺度决策信息系统到第K-1 个单尺度决策信息系统的序贯过程中状态集合变化如图3 所示.

图3 序贯三支决策过程中状态集合的变化Fig.3 The change of state set in sequential three-way decision process
命题1多尺度决策信息系统分层后得到K个单尺度决策信息系统,依次在K个单尺度决策信息系统上进行序贯三支决策,在每个尺度得到的全部三个概率区域有包含关系,下面结论成立:
定义11对于给定的多尺度决策信息系统S=(U,A∪{d},V,F).经过上述定义的K个单尺度决策信息系统的序贯三支决策,最终关于决策类D的三个概率区域定义为:
2.3 相对损失函数的计算假设多尺度决策信息系统中的数据均已经过处理,是形式统一的数值型数据.数据处理方式可参考文献[22].

表10 基于属性值的相对损失函数Table 10 The relative loss function based on attribute value

表11 相对损失函数的汇总Table 11 Summarized relative loss function
表11 列出了所有对象在的所有属性下的相对损失函数,中的对象xi在第j(1 ≤j≤q)个粒度结构下的综合相对损失函数为:
2.4 阈值的计算在第h个单尺度决策信息系统Sh中,xi在属性下由相对损失函数计算得到的阈值为:
由定理1 和定理2 可得,σ减小时,进行三支决策对应的正域和负域减少,边界域增加,即不确定性增加;σ增大时,进行三支决策对应的正域和负域增加,边界域减少,即不确定性减少.因此,可以认为σ的取值大小反映决策者对犹豫和不确定性的偏好.因此,本文将σ作为风险规避系数来说明决策者对犹豫决策风险的厌恶程度,风险规避系数越大,决策者越不愿意作出犹豫决策.
在序贯三支决策过程中,随着属性个数的不断增加,确定性信息增加,可以认为承担风险的能力也增加.于是,设定在第h个单尺度决策信息系统Sh上,计算每个对象在属性(1 ≤j≤q)下的相对损失函数时随着j的增大而逐渐增大,但不超过0.5.
为叙述方便,引入以下记号:
关于σ求导:
所以,随着σ的增大而减小.
所以,随着σ的增大而增大.
2.5 三支决策规则给定第h个单尺度决策信息系统Sh,在第j个粒度结构下,决策属性将论域划分为和¬,分别对应“好”与“不好”的状态.状态集合表示为=/{d}={,¬}.
在Sh的第j个粒度结构下,xi∈的条件概率定义为:
条件概率满足性质:
在Sh的第j个粒度结构下,可得三支决策规则如下:
例3一家公司计划招聘员工,共有10 人前来应聘,记为U={xi|i=1,2,…,10}.面试官以工作能力(a1)、表达能力(a2)、工作经验(a3)和工作潜能(a4)四个标准对面试人员进行评分,并假设四个标准对是否录用面试人员有相同的作用,即权重相同.评分表中有两种评分信息,第一种是对面试人员打分,分值范围为1~10,第二种是“差”“中”“良”的评价.决策为“1”代表聘用,决策为“0”代表不予聘用,最终形成多尺度决策信息表S,如表12 所示(注:表12 为处理之后的数值形式表,条件属性均为效益型属性).将表12 中的多尺度决策信息表进行分层,分层后形成的两个单尺度决策信息表如表13 和表14 所示,两个单尺度决策信息系统分别记为S1和S2.

表12 多尺度决策信息系统STable 12 Multi-scale decision information system S

表13 单尺度决策信息系统S1Table 13 Single scale decision information system S1

表14 单尺度决策信息系统S2Table 14 Single scale decision information system S2
表15 S2中属性值的最大值、最小值及的值Table 15 The maximum and minimum values of attribute value in S2 and the value of
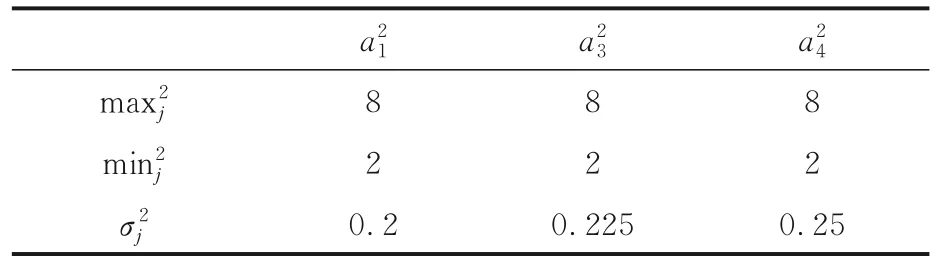
表15 S2中属性值的最大值、最小值及的值Table 15 The maximum and minimum values of attribute value in S2 and the value of
表16 粒度下的相对损失函数Table 16 The relative loss function under

表16 粒度下的相对损失函数Table 16 The relative loss function under
表17 粒度下的阈值Table 17 The threshold values under

表17 粒度下的阈值Table 17 The threshold values under
计算条件概率:
根据决策规则,与表17 中的阈值作比较,可得:
下文中,不同粒度对应的相对损失函数表及阈值表不再单独列出,只给出最终结果.
计算条件概率:
得到的决策划分为:
计算条件概率:
得到的决策划分为:
S2经过三个粒度的序贯三支决策后,关于决策类D2的三个概率区域为:
表18 S1 中属性值的最大值、最小值及的值Table 18 The maximum and minimum values of attribute value in S1 and the value of

表18 S1 中属性值的最大值、最小值及的值Table 18 The maximum and minimum values of attribute value in S1 and the value of
得到的决策划分为:
边界区域为空集,序贯三支决策过程结束.
S1经过一个粒度的三支决策,关于决策类D1的三个概率区域为:
分别在S2和S1上完成序贯三支决策后,得到的全部三个概率区域如下:
最终的决策划分为:
根据决策分类,认为第2,3,4,5,6,8 号面试人员表现优异,可以聘用;第1,7,9,10 号面试人员表现欠佳,不予聘用.
3 结论
本文将多尺度决策信息系统分层后讨论序贯三支决策问题,描述了基于聚类分析和属性依赖度的两种粒度结构的构造方法,提出分层多尺度决策信息系统的序贯三支决策模型,并给出阈值的计算方式及阈值随风险规避系数变化的性质,得到三支决策规则.提出的方法尽可能多地利用了信息解决多尺度决策信息系统的分类问题.
本文研究的背景为经典信息系统,模型应用范围较窄,未来将在模糊背景下进行研究,并将单尺度决策属性推广到多尺度决策属性.
