基于双相准零刚度系统的缓冲隔振超结构设计

王 笑，康 骁

（北京理工大学，先进结构技术研究院，北京，100081）

0 引言

近年来，航空航天中的振动、冲击问题持续引发关注。航天设备在运行过程中容易受到正弦激励、随机激励和冲击等作用，尤其是火箭火工分离过程易对箭体搭载设备产生危害甚至导致设备的损坏，进而影响飞行安全，设计相关缓冲支撑装置对保障设备在冲击环境下的使用安全具有重要意义。围绕以上问题，众多专家学者提出一系列减振措施，使用最广泛的是用粘弹性阻尼材料进行减振的方法［1］，这种方法也被称为阻尼减振方法［2］，例如金鸣等［3］提出的金属橡胶减振器，可以在保证刚度的情况下起到很好的阻尼减振效果。赵程等［4］用金属橡胶和硅橡胶制备了新的复合材料，但所制备的复合材料的实际动态损耗因子不高，此结构在实际应用时局限性较大。

上述缓冲装置如硅橡胶、金属橡胶通过材料的粘弹性或内部金属丝之间滑移、挤压产生的摩擦来消耗能量，达到缓冲隔振效果。然而，其在受到较大冲击后易产生永久变形，影响设备安装定位，塑性变形也阻碍了其再利用，造成了资源与成本的浪费。为解决这一问题，本文引入了基于软硬相复合的双相准零刚度单元的缓冲隔振超结构，该结构由聚乳酸（Polylactic Acid，PLA）准零刚度非线性骨架以及橡胶填充物组成。其中，准零刚度骨架具有高静低动刚度的特点［5-6］，能在满足承载的前提下实现低频隔振的效果，而PLA材料为结构提供了较好的变形可恢复性。橡胶填充物通过产生动态的应力应变，将一部分能量储存为势能［7］，其阻尼特性将另一部分能量转换为热能耗散在空气中。将这两种具有优异力学特性的结构或材料相结合，设计得到的超结构具有优秀的缓冲隔振性能。同时对结构的力-位移承载曲线的设计可满足设备的安装刚度需求。本文利用解析手段结合动力有限元数值仿真对该缓冲结构的缓冲、承载功能进行了设计，并对分离过程的冲击响应进行了计算分析。该研究为火工分离中的设备提供了新的缓冲隔振解决方案。

1 研究背景

1.1 问题描述及缓冲支撑装置的应用背景

在火箭火工分离过程中需要设计缓冲支撑装置，保护设备在冲击环境下的使用安全。如图1所示，设备本体尺寸200 mm×50 mm×50 mm，质量为2 kg，质心在设备形心。设备底部设4 个安装耳片，通孔Φ5.5 mm，使用4 个M5 螺钉安装，螺钉长度可以调整。

图1 设备本体结构Fig.1 Device body structure

1.2 准零刚度结构的优势及应用

随着现代机械设备越来越精密化和轻型化，低频和超低频隔振技术越来越受关注。传统的硅橡胶隔振支座由于自身刚度较大，在低频隔振上效果有限。准零刚度隔振器通过引入负刚度机制能有效降低系统整体刚度，从而在不牺牲承载能力的前提下提高低频隔振性能。这类负刚度力学超材料具有特殊的力学性质，能在受约束条件下吸收和消耗大量能量，并且有可恢复性。因此，其在冲击吸能和减振降噪方面具有很大的应用潜力。

准零刚度振动控制依赖于负刚度机制，目的是用负刚度来抵消正刚度，从而达到接近零的系统刚度，通常通过使用被动或主动/半主动的负刚度机构来实现。被动机构主要包括机械弹［8-9］、预屈曲梁［10-11］、磁性结构［12］、仿生结构［13］和复合结构［14］。

准零刚度结构适合用作缓冲隔振支撑，以往对准零刚度隔振器的研究主要集中在支撑汽车座椅［15］和发动机保护，如图2所示［15］，尚未用于火箭分离。随着增材制造技术的进步，超结构在吸能和隔振方面得到应用。其吸能原理来自单胞中通过屈曲实现的负刚度。串联这些单胞可实现理想的冲击保护和能量吸收。超结构作为一种具有先进机械和物理性能的人造结构，独特的性能严格依赖于内部周期单胞的构型，而非材料的固有属性。

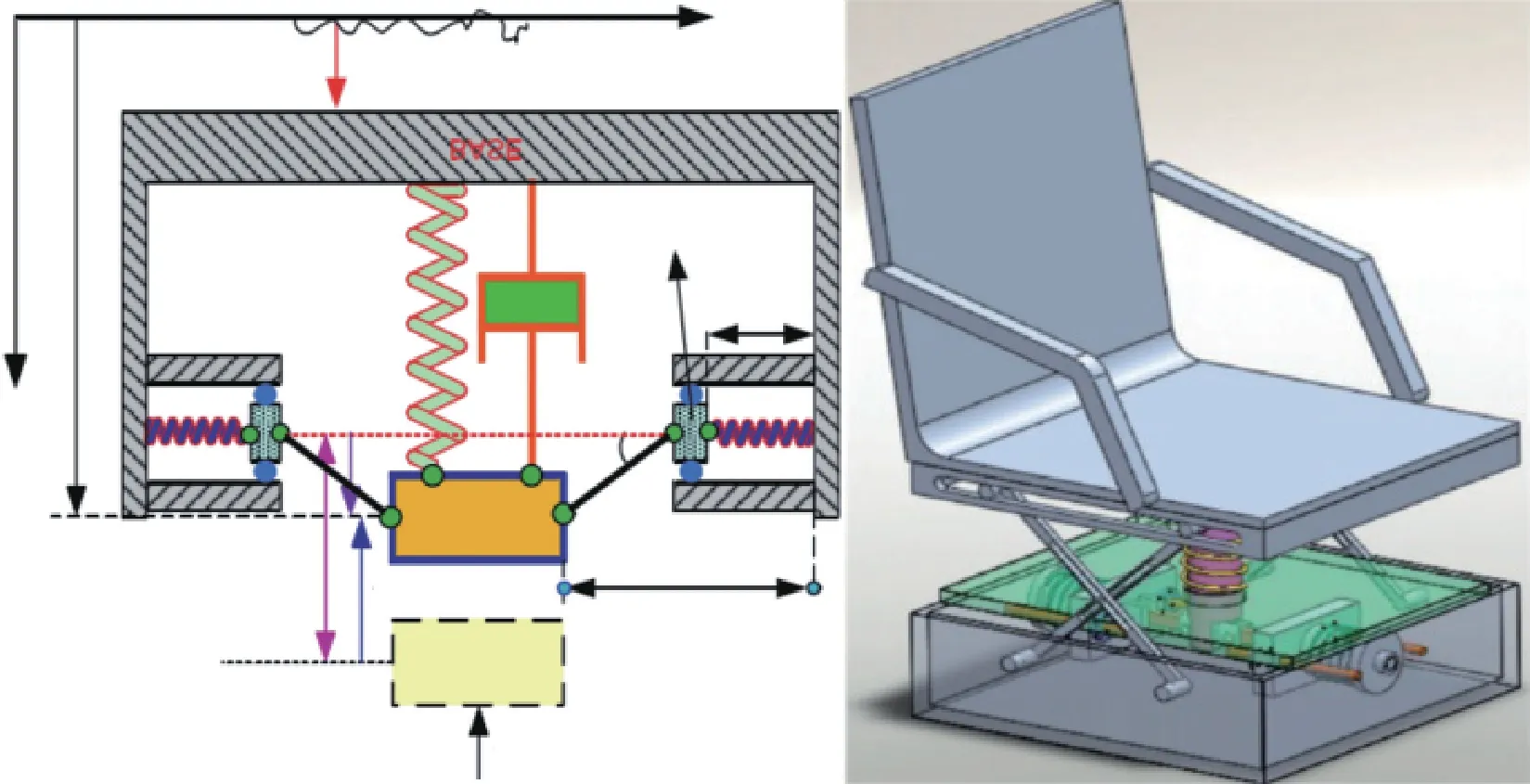
图2 汽车座椅系统的隔振模型Fig.2 Vibration isolation model of vehicle seat system

2 缓冲隔振超结构胞元设计

2.1 结构模型

本文设计的超结构如图3a 所示，其单胞由正弦梁、一对半圆拱和刚性壁组成。由于固支正弦梁在水平荷载作用下呈负刚度，而半圆拱在竖向荷载作用下呈正刚度，通过正负刚度的适当配合可在单胞以及整个超结构中实现准零刚度，如图3b 所示。如图3c 所示，正弦梁的形状由y=h/2［1-sin（2π（x-l1/4）/l1）］给出。正弦梁和半圆拱都通过厚度为t的刚性壁连接。

图3 准零刚度超结构模型Fig.3 Quasi-zero stiffness metastructure model

2.2 超结构的力学模型

正弦梁在中心施加位移的力学行为可以通过使用直固梁屈曲模态的模态叠加来近似模拟。根据文献［16］，当正弦梁的参数满足h/t1≥6 时，其力-位移曲线可以近似地用3 条相连的直线表示，如图4所示。

图4 正弦梁与半圆拱的力-位移曲线Fig.4 Force-displacement curve of the sinusoidal beam and the semicircular arch

力-位移曲线中相应的参数如下：

式中E为构成材料的杨氏模量；I1为梁的转动惯量。正弦梁在这3个不同阶段的刚度可推导为

对于以弯曲为主的半圆拱，竖向位移作用下的力-位移曲线可近似表示为正刚度弹簧单元，如图4所示。根据梁理论，半圆拱的刚度与组成材料的杨氏模量E、半圆拱的转动惯量I2和半圆拱长度l2的立方的倒数成正比。因此，半圆拱的刚度可表示为

其中α是一个无量纲系数。需要注意的是，不同截面对应的无因次系数既可以通过弹性分析求得，也可以通过有限元法求得。

当正弦梁和半圆拱串联，竖向位移作用下的单胞刚度为两者刚度之和，因此，单胞的力-位移曲线也可以用3条相连的直线表示。通过调节正弦梁和半圆拱的结构参数来调节刚度，满足2kb稍大于ka2的绝对值，在如图5 所示的Ⅱ区域获得准零刚度。单胞的刚度表达式可由式（4）求得：

图5 单胞的力-位移曲线Fig.5 Force-displacement curve of unit cell

图3b显示超结构由水平和垂直排列的单胞组成。假设水平方向的单胞数为m，垂直方向的单胞数为n。根据串并联弹簧理论，具有（m，n）个单胞的超结构的刚度和相应的垂直位移为

根据实际工程中的设备质量来确定承载需求，根据力-位移承载曲线反向设计可满足设备安装刚度需求的超结构，同时调整正弦梁和半圆拱使其刚度相互配合来获得低动刚度满足隔振性能。

3 隔振性能分析

3.1 静力数值模拟

使用软件进行有限元分析以研究受压超结构的力学性能。如图6所示，分别计算了准零刚度单胞与双相准零刚度单胞的静力学性能，结构参数l1=10 mm，t1=0.2 mm，h=1.2 mm，b1=10 mm，l2=6 mm，R=1.5 mm，b2=10 mm，t2=0.31 mm，t=10 mm。超结构采用20 节点二次方块、简化积分实体单元（C3D20R）建模，并进行网格灵敏度收敛研究以确保准确性。超结构底部完全固定，顶部表面与参考点耦合并在五个自由度上受到约束，通过对顶部参考点施加恒定的速度载荷来对整个结构进行加载，同时约束结构两侧仅允许压缩方向的位移。只允许在压缩方向上进行平移。模拟中准零刚度骨架为PLA，其生产原料为可再生能源，可降解，对环境友好，并且有较好的强度和延展性。采用弹塑性模型对PLA 进行有限元仿真计算，材料参数［17］见表1。橡胶采用Mooney-Rivlin 超弹性本构模型，在小应变范围内（0～100%拉伸和30%压缩）能够较好地表征橡胶材料的力学行为，材料参数见表2。

表1 PLA材料参数Tab.1 Material parameters of PLA

表2 橡胶材料参数Tab.2 Material parameters of rubber

图6 单胞的有限元模型Fig.6 Finite element model of unit cell

3.2 模拟结果分析及数学模型建立

图7为准零刚度单胞与双相准零刚度单胞在顶部表面相同位移D下的变形结果，输出结构的力-位移曲线如图8所示，在初始阶段，正弦梁和半圆拱均为正刚度，反作用力随着位移的增大而迅速增大。当压缩位移超过一定值，正弦梁会经历一次失稳突变行为，从而产生负刚度特性，与半圆拱的正刚度叠加使得结构出现准零刚度特性，随着压缩位移继续增大，正弦梁过渡到另一个稳态结构，结构总刚度增大到正值。对比图8中的力-位移曲线发现，有橡胶填充的双相准零刚度单胞相较于无填充的准零刚度单胞的承载明显提高，说明其抵抗变形的能力增强。

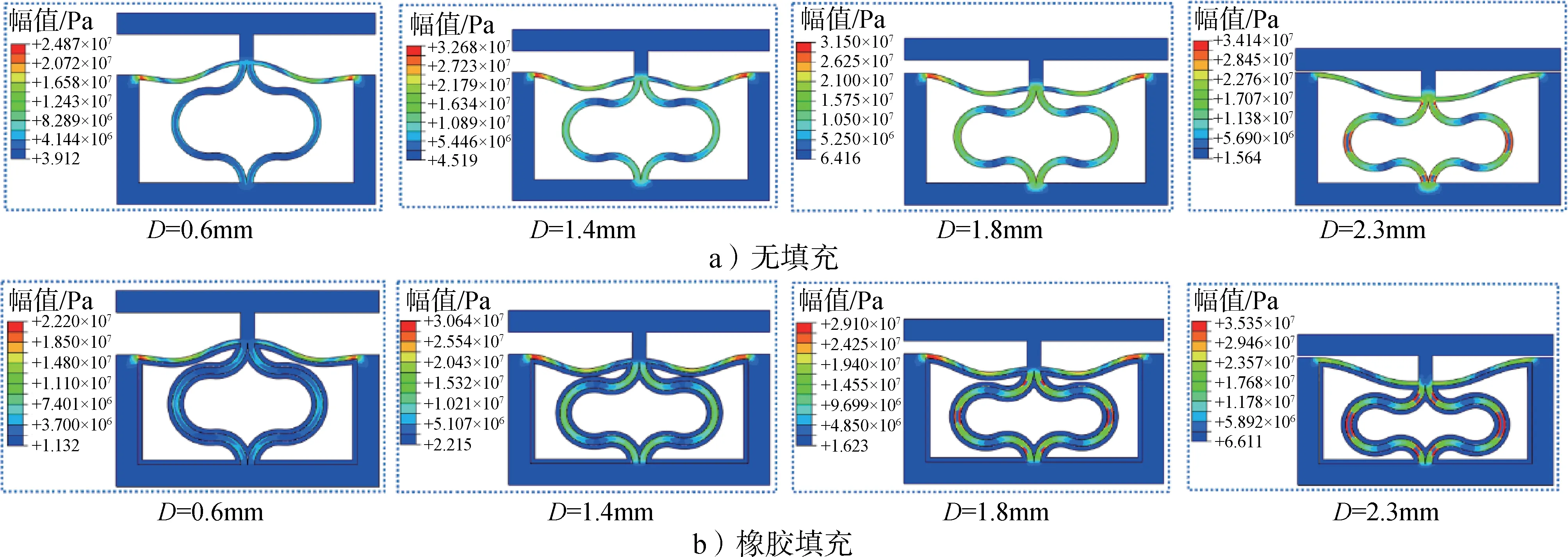
图7 单胞位移云图Fig.7 Displacement nephogram of unit cell

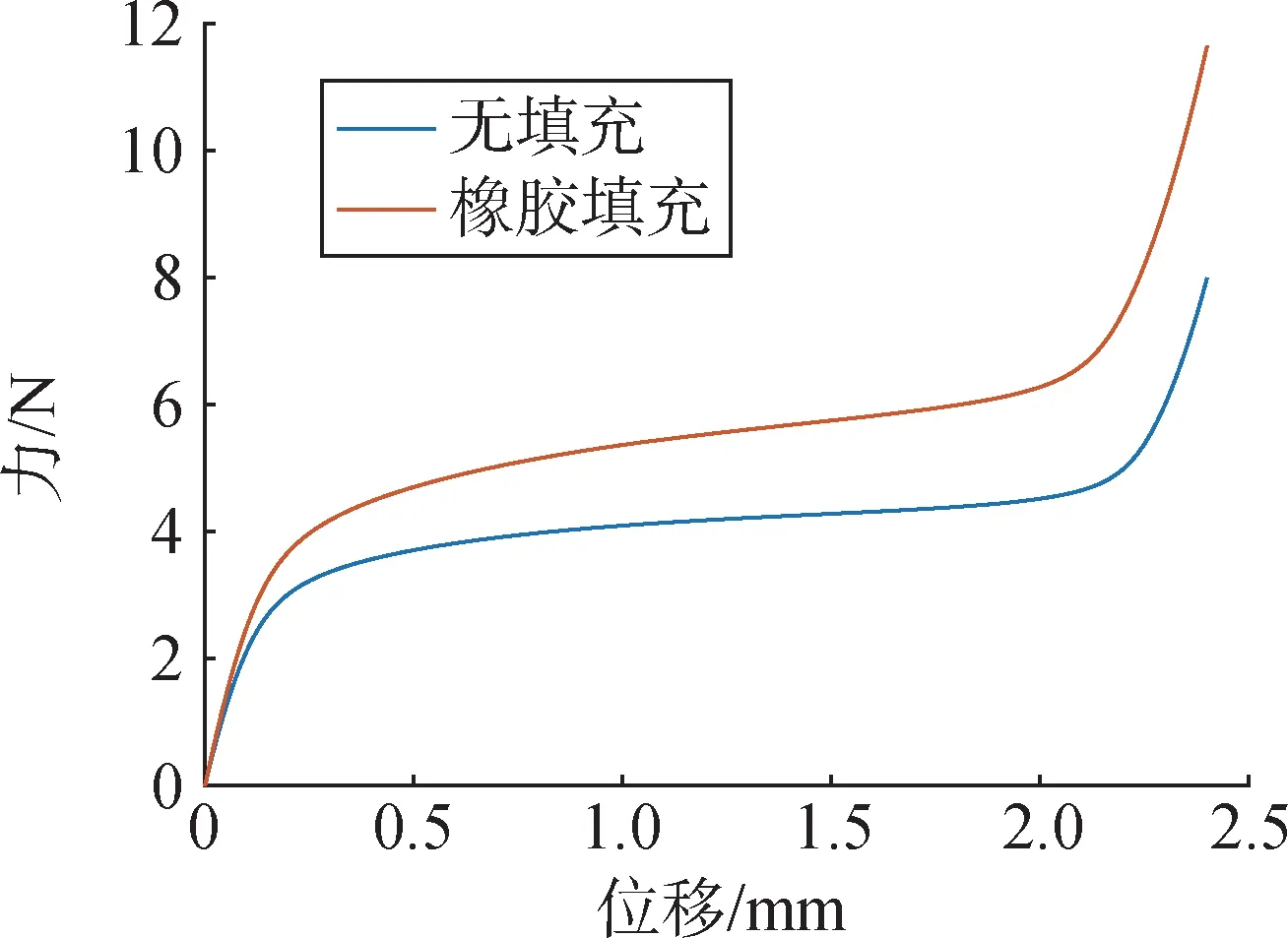
图8 力-位移曲线对比Fig.8 Comparison of force-displacement curve

通过图7可以看出结构会产生大变形，具有很强的几何非线性，难以得到结构力-位移曲线的解析公式。因此采用基于有限元静力计算结果的拟合曲线来表示结构变形过程的静力学关系。采用数据拟合工具箱运用三次多项式拟合，以设计静平衡位置为位移坐标零点，以设计静承载力为力坐标零点，对力-位移曲线进行平移，平移后的曲线如图9所示，曲线初始部分具有较高的静刚度，为承载段，能够支撑较大的质量。静平衡位置附近的准零刚度段，具有极低的动刚度，为隔振段，能够实现低频隔振。

图9 力-位移曲线及其多项式拟合曲线Fig.9 Force-displacement curve and polynomial fitting curve

双相准零刚度单胞的回复力与位移的关系写成三次多项表达式为

式中K1，K3分别为一次和三次多项式的拟合系数，本算例中K1=0，K3=1.9 N/mm3。

将双相准零刚度隔振系统简化为单自由度质量-弹簧-阻尼系统，如图10 所示。考虑阻尼C的影响，被隔振体质量M使系统处于静平衡位置，在简谐激励fB=Fcos（ωt）的作用下，非线性动力学系统的单自由度有阻尼受迫振动运动方程为

图10 双相准零刚度隔振系统力学模型Fig.10 Mechanical model of dual phase quasi zero stiffness vibration isolation system

无量纲化后：

3.3 幅频特性曲线

采用谐波平衡法来求解双相准零刚度隔振系统的非线性运动方程（9），忽略高次谐波项，设系统的主共振响应为

式中A为系统响应的幅值；Ω为简谐激励频率；θ为系统响应的相位，均为常数。将此解代入式（9），求得系统幅频特性方程如下：

从式（11）中可以看出，响应幅值A随激励力的变化是非线性的，并且受到阻尼比ζ和激振力幅值F的影响。通过数值计算得到阻尼比对幅频特性的影响如图11所示，其中γ1为0，阻尼比会影响系统跳跃现象，随着阻尼比增大，幅频特性曲线向右弯曲的程度逐渐减小，响应幅值峰值也减小。当阻尼比增大到0.1时，达到临界阻尼比，此时系统的跳跃现象消失。

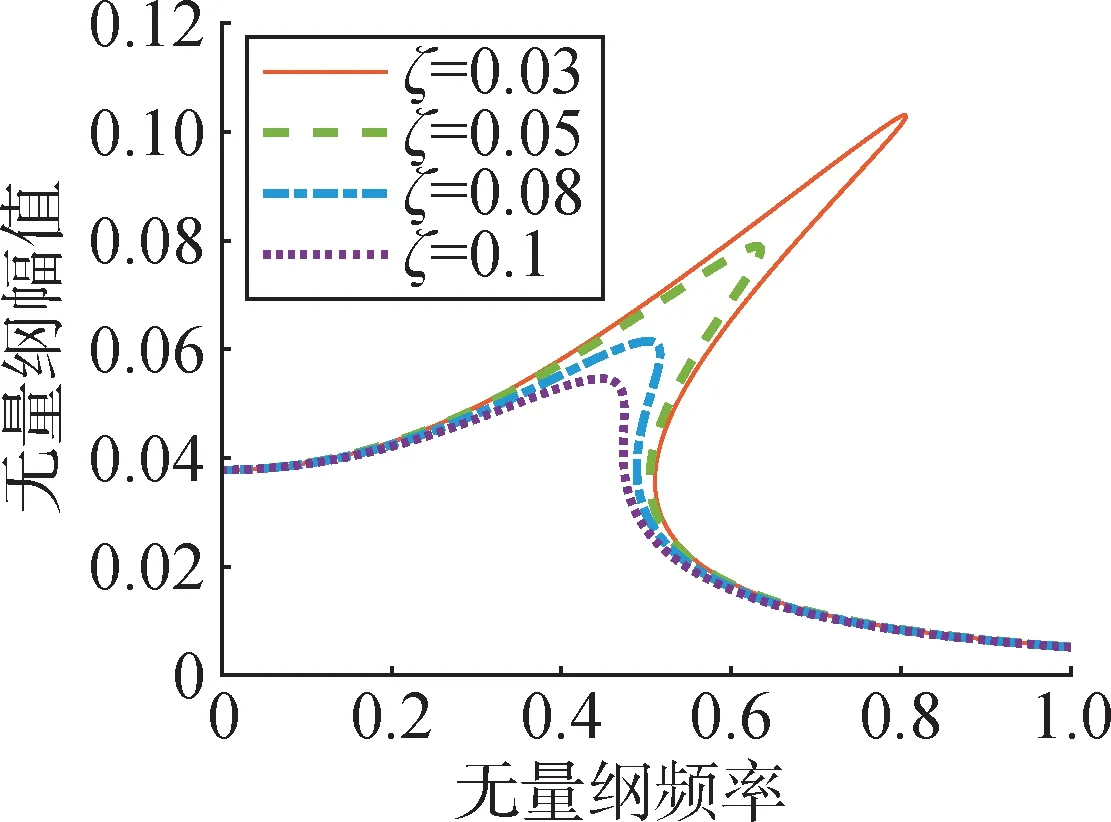
图11 当γ3=75,=0.005时阻尼比对系统幅频特性曲线的影响Fig.11 Influence of damping ratio on amplitude-frequency curves of system for γ3=75,=0.005

图12 当γ3=75,ζ=0.05 时激振力幅值对系统幅频特性曲线的影响Fig.12 Influence of exciting force magnitude on amplitudefrequency curves of system for γ3=75,ζ=0.05

3.4 力传递率

力传递率是评价隔振器隔振效果的指标，对于单自由度线性系统，力传递率T可以定义为隔离质量M所受力Ft与外部激振力F之比，用分贝的形式表示为

而双相准零刚度系统的力传递率与阻尼比和激振力幅值有关，无量纲化后用分贝形式表示为

图13 为双相准零刚度系统与其等体积的橡胶隔振系统的力传递率对比。双相准零刚度系统的无量纲刚度γ1=0，γ3=75，橡胶隔振系统无量纲刚度γ1O=2 280。当传递率小于0 dB 时，隔振系统才具有隔振效果，从图13 可以看出，线性隔振系统的幅频特性曲线没有跳跃现象，通过选取合适的激振力幅值，双相准零刚度系统的隔振起始频率显著低于其等体积的橡胶隔振系统，有效隔振频带更宽。这表明双相准零刚度系统在保证承载的前提下具有更好的隔振效果，解决了传统橡胶类线性隔振系统因自身刚度大而无法实现低频隔振的局限性问题。

图13 当ζ=0.03,=0.1 时橡胶隔振系统和双相准零刚度系统的力传递率比较Fig.13 The comparison of force transmissibility between rubber system and phase QZS system for ζ=0.03,=0.1

4 缓冲性能分析

4.1 双相准零刚度系统阻尼能量耗散机制

当结构受到冲击时，准零刚度骨架在振动过程中反复拉伸、压缩内部橡胶填充物，导致橡胶内部产生摩擦并耗散能量。由于PLA的刚度远大于橡胶，当准零刚度骨架变形时，靠近骨架界面的橡胶变形小，远离骨架界面的变形大，这种不一致的变形使得PLA和橡胶之间的界面产生粘滞效应，进一步产生相应的阻尼耗散。

4.2 冲击动力学数学模型建立

为了便于分析，将缓冲系统简化为单自由度无阻尼线性系统，如图14a所示。其中相对基础位移为δ，根据相对坐标系的动量定理，以δ为广义坐标，建立缓冲系统动力学模型为

图14 计算数学模型Fig.14 Computational mathematical models

为求得微分方程（14）的解析解，依据加速度增量相等原则，把输入加速度的脉冲曲线转换为便于计算的矩形脉冲曲线，如图14b所示。

其中矩形脉冲加速度时程的峰值为，加速度持续时间为

把初始条件δ(0)=0 和(0)=0 代入微分方程（14），考虑脉冲加速度作用时间非常短，满足参数条件ωnτ≪1，可得：

因此缓冲物体绝对加速度为

加速度最大值为

由式（19）可以看出，当冲击时间非常短时，在一定冲击强度下，弹性系统的刚度k越小，缓冲物体绝对加速度越小，而准零刚度系统在静平衡位置具有低动刚度，因此具有优秀的缓冲能力。

4.3 双相准零刚度系统冲击仿真

对于考虑阻尼的非线性动力学系统，很难求得其冲击响应的解析解，为研究双相准零刚度系统对于爆炸分离冲击响应的防护效果，进行动力学仿真计算。将上文中所设计的单胞进行了2 行4 列的阵列，并结合所需保护的设备本体进行耦合仿真计算，有限元仿真模型如图15所示。材料参数与第3.1节一致。结构的底部表面完全固定，设备本体通过绑定约束和隔振器进行连接。

图15 有限元模型.Fig.15 FE model

为了模拟冲击的实际行为，通过对整个模型施加y方向的冲击加速度载荷来对整个结构进行加载，提取设备中部测点的冲击加速度，通过对比输入与输出的加速度幅值来验证结构的缓冲减振效果。选择三维应力缩减积分单元C3D8R 进行计算，在此基础上进行瞬态数值仿真求解。

4.4 结果分析

当结构受到冲击后，橡胶的阻尼特性将能量转换为内能进行耗散，同时橡胶和PLA 框架会发生挤压、摩擦，该过程也会消耗大量能量。图16为结构受到y方向加速度载荷时的应力云图，其中对变形进行了2倍放大。可以看出在t=1.5 ms 时结构变形达到最大，之后发生回弹，由于惯性作用，在回弹过程会出现拉伸，在t=3.8 ms 时，拉伸变形达到最大，最后在t=4.8 ms时基本恢复到初始状态，整个过程中模型变形发生在弹性阶段，受到冲击后能复原，准零刚度骨架为结构提供了良好的变形可恢复性。

图17b 为结构受到y方向加速度载荷时测点的输出与输入时域加速度对比，输入加速度约为8 000g，输出响应降低90%以上。图17e 为结构受到y方向加速度载荷时测点的输出与输入冲击响应谱对比，输入峰值为7 600g，输出响应在大于200 Hz 的频带段明显衰减，其峰值衰减90%以上。由于对结构的防护要求在整个空间内都有效，同时计算了x方向和z方向的缓冲效果，见图17，时域加速度和冲击响应谱的峰值都显著降低，验证该结构可有效降低爆炸分离过程中的冲击响应，从而保障设备在冲击环境下的安全使用。

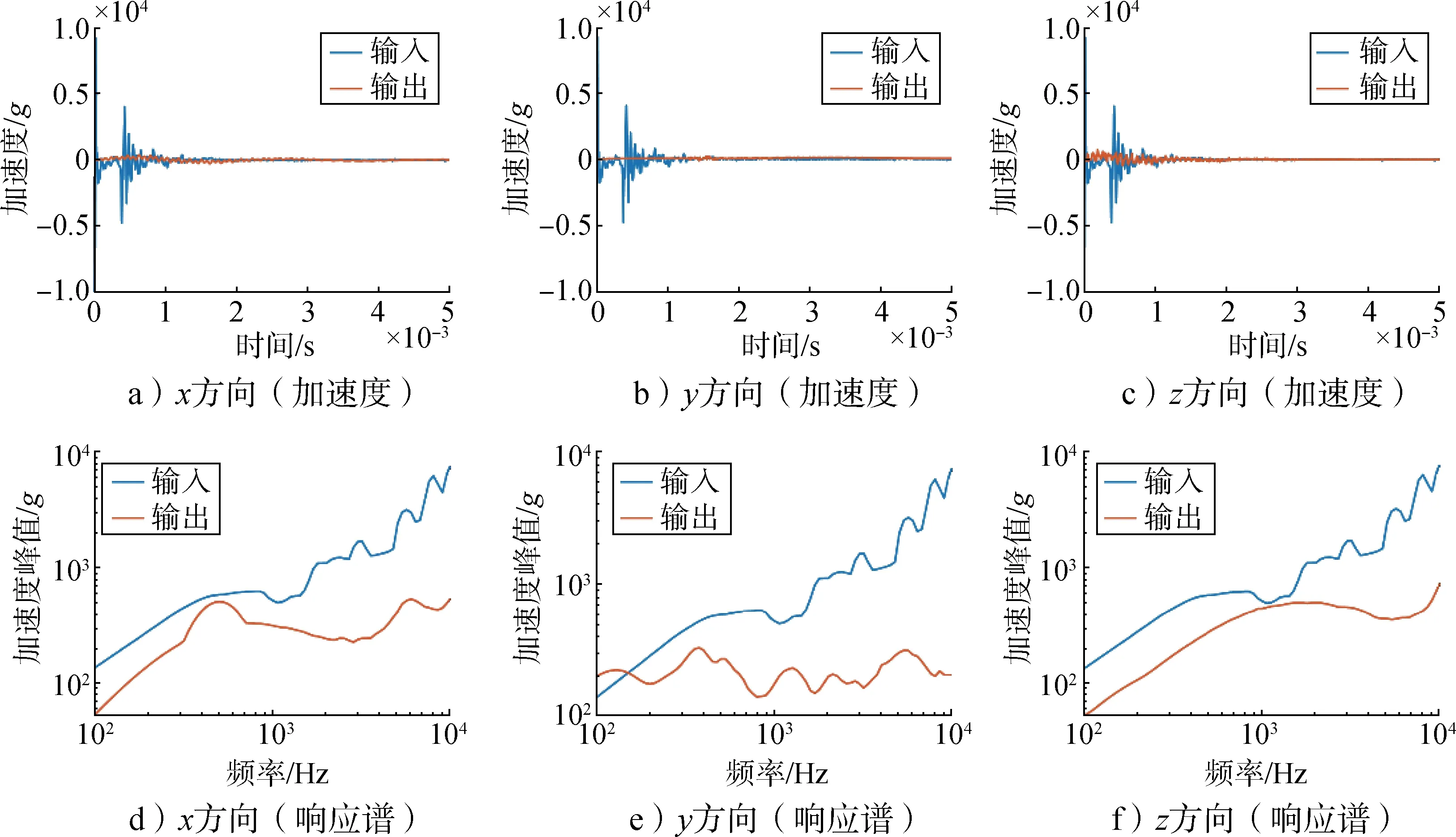
图17 加速度时程曲线与冲击响应谱对比Fig.17 Comparison of acceleration time-history curves and shock response spectra

5 结论

本文设计并研究了一种用于隔振的双相准零刚度超结构。结合理论和仿真方法对超结构的隔振特性和缓冲性能进行了研究。

对所提出的超结构的隔振缓冲性能进行了评估，结果表明所提出的双相准零刚度超结构比橡胶类隔振器具有更优异的隔振性能，同时具有良好的变形可恢复性，在缓冲隔振应用中具有巨大的潜力。研究得出以下结论：

a）通过适当设计正弦梁和半圆拱，可以实现具有准零刚度特性的单元。推导了单元和阵列后的结构的力学性能理论解。

b）通过力传递率的对比，可以看出双相准零刚度系统比线性橡胶系统有效隔振频带更宽，在保证承载的前提下隔振效果更好。

c）数值模拟的应力云图揭示了双相准零刚度超结构隔振系统相比于传统硅橡胶有更好的变形可恢复性，克服了硅橡胶永久变形和不可重复利用的问题。

d）测点的时域输出响应和冲击响应谱揭示了双相准零刚度超结构隔振系统可显著降低冲击响应，冲击响应谱加速度峰值降低了90%以上。