基于深度学习和影响函数法的机翼非定常流场预测

于煜斌，落龑寿，缪 佶，曹隽喆，李京杰

（1.北京宇航系统工程研究所，北京，100076；2.大连理工大学，大连，116024）

0 引言

现代飞行器设计需要对其周围流场进行细致的研究，诸如飞机机翼的气动振颤、操纵面的嗡鸣、战斗机的过失速飞行等都与非定常扰流有着密切的关系［1］。准确地求解非定常流场对于飞行器的研制至关重要，但是相关工程问题的复杂性会导致试验技术难度及耗费的增加。因此，开展对飞行器非定常流场的动态数值模拟研究对于飞行器气动外形设计和动态失速机理的研究有着重要意义［2］。

目前基于计算流体力学的飞行器模拟飞行数据的方法，虽然理论可靠性和计算准确率较高，但计算速度较慢，已经不能满足日益增长的设计需求对模拟飞行数据计算速度的要求。随着最近几年卷积神经网络和深度学习的快速发展，其突出的非线性映射能力吸引越来越多的学者将这种方法运用到流体力学领域［3］。卷积神经网络最初用于解决图像相关问题，近年来也被用于处理时空序列问题。卷积神经网络发源于人类对图像的认知形式，即对图像中相近的区域进行一系列分辨，判断对应位置的图形信息。为此，卷积神经网络通过卷积核对图像进行分块卷积运算，以及分区域的特征提取和学习。而随着批归一化和残差连接在神经网络中的应用，深层神经网络的训练过程变得更加容易，其性能退化问题也在一定程度上得到了解决。

刘昕［4］提出了一种基于径向基函数（Radial Baisi Function，RBF）的神经网络模型，并将其成功运用到机翼沉浮振动中的机翼升阻力预测。Balla 等［5］提出了一种多输出的神经网络来进行二维和三维机翼的气动系数预测，并与本征正交分解（Proper Orthogonal Decomposition，POD）方法进行比较，结果表明神经网络具有更好的性能，特别是在预测包含激波的流场时。Miyanawala 和Jaiman［6］在2017 年首次实现深度卷积网络通过二维柱体尾迹区流场变量对气动载荷的准确预测。惠心雨等［7］基于深度学习提出了一种非定常周期性预测方法，可以实时生成给定状态的高可信度流场结果。

神经网络虽然在气动参数预测中表现优异，可以得到传统拟合所不能达到的较好的非线性拟合效果，但是由于非定常流场问题需要考虑流场域空间各单元之间的相互影响，因此在训练网络时如何将这种影响信息准确引入到学习过程中是一个关键的问题，但目前几乎没有文献对此进行研究。

针对上述问题，本文将数理方程中影响函数的概念引入到深度学习中来构建神经网络［8］。将每个数据点的影响用一个数学函数形式化建模，该函数被称为影响函数。影响函数法是一种离散化的方法，它的基本思想是将移动边界表面离散成若干网格，移动边界发生的变形也按相同网格离散化，应用影响函数可以先确定移动边界各节点对其他网格节点的影响，再叠加出各网格受到的总影响［9］。该方法是基于已知试验数据及仿真数据建立的数据集，通过训练构建神经网络模型实现快速网络化并用于非定常流场预测。

1 研究方法

1.1 算法构建

对于非定常流场预测问题，网格间的相互影响可以通过建立相应的影响函数来描述，其边界节点的运动信息作为一种流体扰动向四周空间传播并衰减，当前网格节点受到的扰动向周围流场扩散，每个流场空间节点获取当前位置的扰动信息，并对它作出相应的反应，这种扰动的扩散衰减机制通过影响函数来实现。

假设流体流经一个空间位置固定的无穷小微团，如图1 所示，其速度和密度都是关于空间坐标(x，y，z)和时间t的函数，即微团影响函数。对于不同离散化方法生成的网格，每个网格单元就可以看作是一个无穷小微团，若采用有限体积法将计算区域离散为若干网格，则每个控制体积就可以看作是一个小微团。微团移动边界发生的变形也按相同网格离散化，移动边界的运动信息可以定义为一个数据集合，这个数据集合是每个边界节点的移动信息，包括节点的坐标和节点的位移量，相关数据可以来自于真实测量数据、风洞试验和仿真模拟结果。

图1 无穷小微团示意Fig.1 A schematic of infinitesimal clumps

基于上述假设，本文建立如下的算法构建微团的影响函数：

a）无穷小微团aj=(xj，yj，zj)对无穷小微团ai=(xi，yi，zi)的影响记为g(xj-xi，yj-yi，zj-zi)，无穷小微团可用数值仿真中网格单元或实际试验中的采样数据表示；

b）将坐标轴上不同区域D对(xi，yi，zi)的影响构建为区域内其它小微团对(xi，yi，zi)影响的加权和gD(x)=∑()x，y，z∈Dwig(xj-xi，yj-yi，zj-zi)，使用欧几里得距离作为权重wi；

c）影响函数定义如下：

影响函数的类型包括线性影响函数：

二次影响函数：

指数影响函数：

式中d(aj，ai)为aj至ai的欧氏距离；dmax为两个节点之间的最大距离；α为一个常数。

1.2 卷积神经网络

本文采用的卷积神经网络框架如图2所示，并引入如图3所示的基于影响函数的注意力机制，使得模型在训练与预测中间环节能进一步考虑到流场数据无穷小微团间的空间影响，进而辅助在计算网格密度变化较大的地方提高控制方程数值求解的效率，提升整体仿真性能。

图2 卷积神经网络框架Fig.2 Convolutional neural network framework

图3 注意力机制Fig.3 Attention mechanism

在训练网络时，使用如下加权误差平方和作为损失函数：

式中yi与分别为无穷小微团的真实物理量与估计值（生成量）；gDi为无穷小微团所处区域的影响函数。

在构建网络时，本研究使用以下RANS-SA 方程产生训练数据：

在训练模型时，采用以下两种机制：

a）早停机制：理想情况下，模型在训练集上的损失函数值将随迭代次数的增加不断减小，并无限逼近最小值。此时，若随着迭代次数的增加，模型在验证集上的损失函数值不再变化甚至变大，则模型继续训练将导致过拟合而不再具有良好的泛化能力。因此，在试验中引入早停机制，模型在训练集上进行训练时，每轮训练后在验证集上进行验证并比较效果，当模型在验证集上的性能连续5轮不再改善时，则停止训练，保存验证效果最好的一次模型参数并用于预测。

b）Dropout 机制：Dropout 机制可有效防止模型过拟合，其原理为在训练过程中，暂时丢弃部分神经元及其连接，使之在该轮训练中不再参与前向传播计算及反向参数更新，在多次迭代中将更加关注激活状态的神经元，进而避免了所有参数的协同适应问题。本质上每次Dropout 均修改了神经网络结构，使得最终模型可被视为多个模型集成的结果，进而避免了模型的过拟合现象。在本文中，模型正则化Dropout 比率设定为0.2。

1.3 流场预测方法

为了将各网格单元的相互影响加入网络学习中，本文将1.1 节中设计的影响函数嵌入深度学习网络的训练过程中，使模型在流场数据的拟合、预测时能够对无穷小微团间相互影响进行自适应。而在构建深度学习网络时，采用了残差连接方法，该方法在卷积层之间建立恒等映射，使得深层网络得到的特征相比浅层神经网络不会出现损失。所建立的深度学习主干网络结构如图4所示。

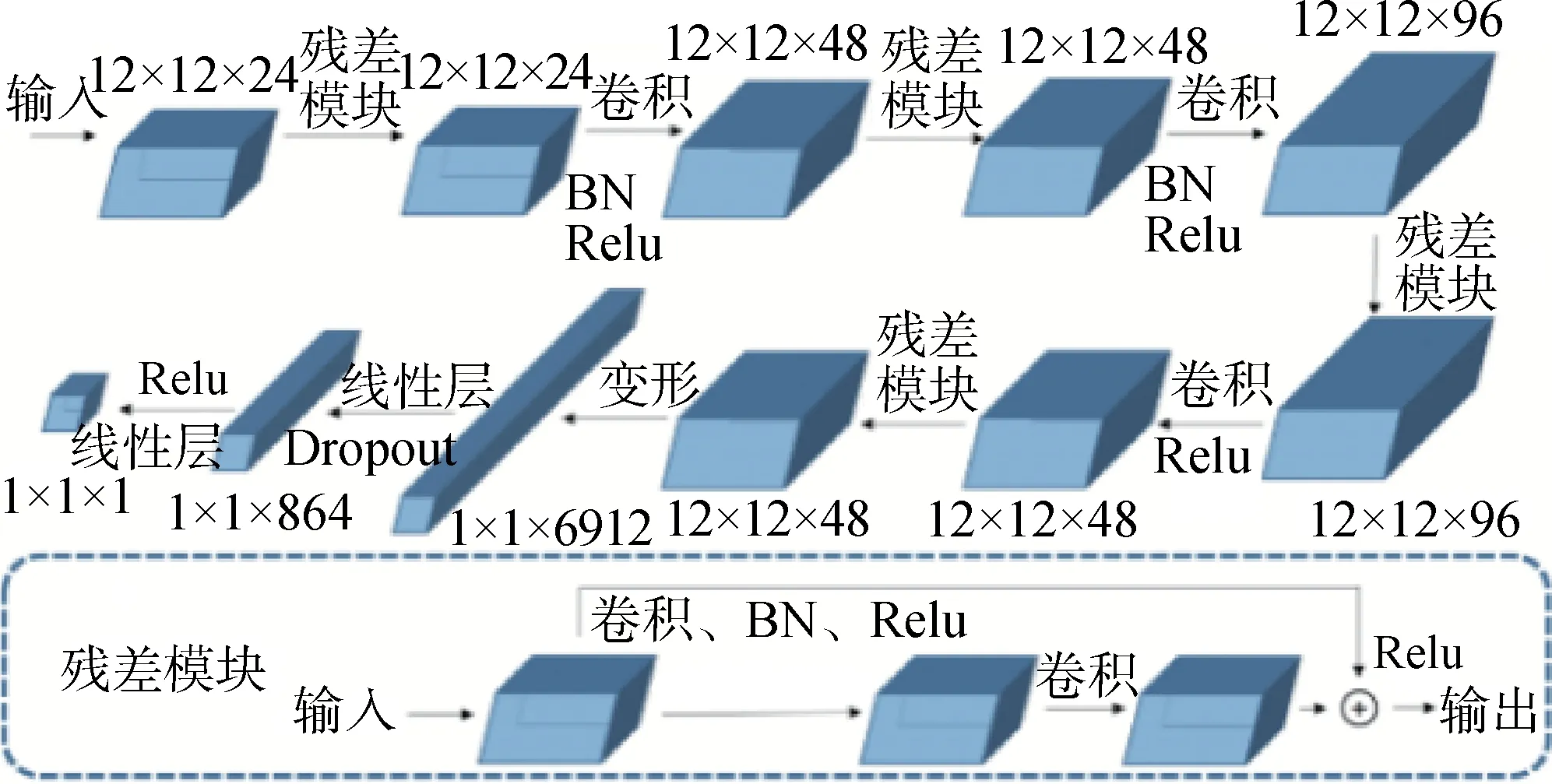
图4 主干网结构Fig.4 Backbone network structure

基于上述的影响函数和深度学习网络，本文采用如图5所示的方法进行非定常流场的预测。首先利用试验或仿真数据的空间坐标信息作为影响函数的输入生成权重，然后基于所得权重与数据构建神经网络，最终生成流场预测数据。该方法利用影响函数确定移动边界各节点对其他网格节点的影响叠加，并将其导入深度学习过程，能够对非定常流场进行可靠预测。

图5 基于深度学习与影响函数的流场数据生成流程Fig.5 Flow field data generation process based on deep learning and influence function

2 算例与数值试验

2.1 算例描述

算例采用经典的RAE 2822翼型［10］，如图6所示。该翼型是一个典型的二维跨声速湍流流动算例，本文分别对其采用CFD仿真软件和所提出深度学习模型进行了数值计算对比试验。测试数据为速度为1马赫的机翼周围流场，整个求解区域的网格量约为180 万个，初始攻角为0。

图6 RAE 2822翼型示意Fig.6 Schematic diagram of RAE 2822 airfoil

2.2 数值试验

试验随机选择10 000个网格的气动数据作为微团训练集构建深度学习网络，再随机选择其他60 000个网格的气动数据作为测试集进行验证，采用决定系数R2表示深度学习网络的效果。决定系数R2可理解为模型输出与实际数据间相关系数的平方，当R2≥0.8时模型具有良好的预测性能。

图7～10给出了本文方法与仿真软件所生成流场数据在训练集和测试集的拟合结果。计算采用一台2个CPU 的工作站进行并行计算，每个CPU 为10 核的Intel Xeon E5-2650 v3，主频2.0 GHz，内存共128 GB，并采用一张含有4 992 颗CUDA 核心的NVIDIA Tesla K80 深度学习显卡以检测GPU 加速效果。

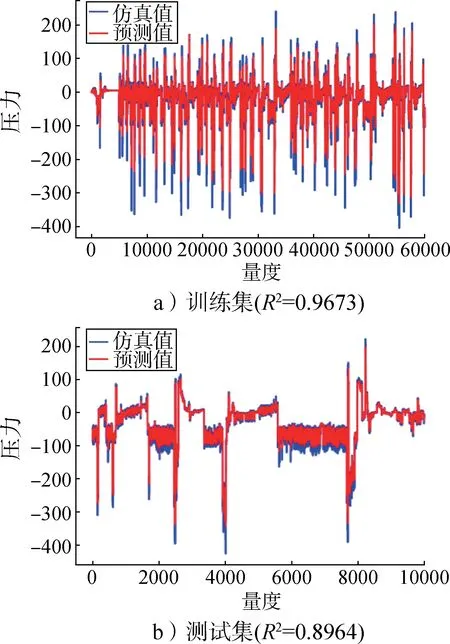
图7 训练集和测试集表面压力拟合结果Fig.7 Surface pressure fitting results of training set and test set

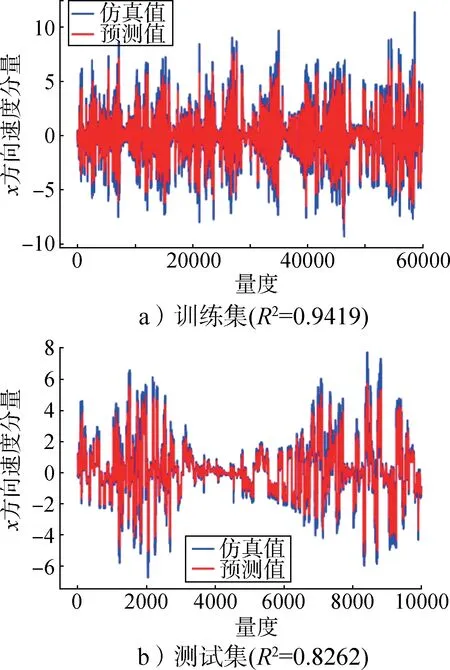
图8 训练集和测试集速度x分量拟合结果Fig.8 Speed x component fitting results of training set and test set

图9 训练集和测试集速度y分量拟合结果Fig.9 Speed y component fitting result of training set and test set

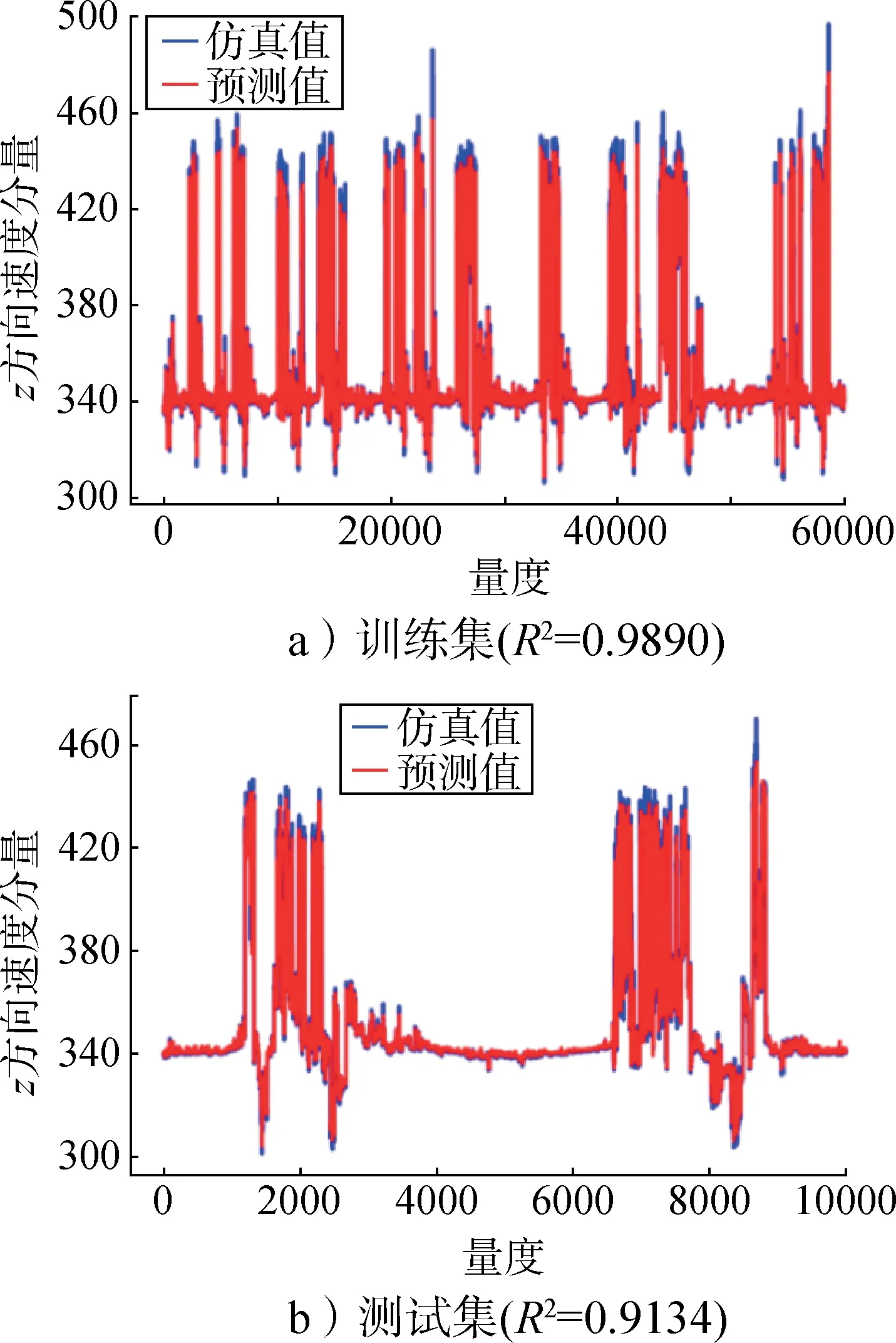
图10 训练集和测试集速度z分量拟合结果Fig.10 Speed z component fitting result of training set and test set

表1给出了CFD计算时长和深度学习网络预测时长的比较，可以看到本文所构建方法的计算效率明显优于传统CFD方法。在只采用CPU进行计算的时候，深度学习网络用于训练和预测的总时间比传统CFD计算总时间相差至少一个数量级，而在采用GPU 加速之后，CFD计算时间只降低了10%左右，提升的效果较为有限；而深度学习方法则在经过了GPU 加速后计算用时得到了极大的缩短，计算效率提升了11倍，这是因为深度学习网络的迭代计算方式能较为充分调用CUDA 和底层硬件进行并行计算任务，因此GPU加速效果明显。

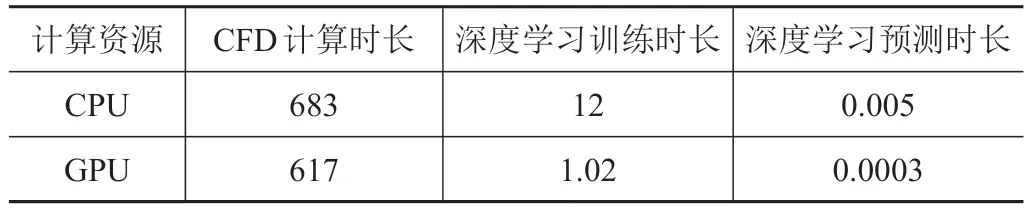
表1 CFD计算时长和深度学习网络预测时长Tab.1 CFD calculation time and deep learning network prediction time 单位：min

3 结束语

本文提出了一种基于深度学习和影响函数法的机翼非定常流场预测方法。该方法不需要求解复杂的离散方程，而是利用已有的试验或仿真数据训练深度学习网络并快速输出预测结果，且在只有少量数据情况下仍可以有效建模，从而具有更快的气动数据拟合、预测与插值速度。

通过本文的研究，说明深度学习在机翼流场数值仿真计算方面具有较大的发展潜力，可以通过增加网络层数、卷积核数量、迭代次数和设计有效的损失函数等措施，加大深度网络的拟合和泛化能力，从而适应更加复杂的翼型。