基于EEMD-LVQ的机电作动器故障诊断方法

王晓明，付继伟，韩 松，白云鹤，李少石

（1.北京宇航系统工程研究所，北京，100076；2.北京航空航天大学，自动化科学与电气工程学院，北京，100191）

0 引言

机电作动器（Electronic-mechanical Actuator，EMA）是现代装备功率电传系统的核心技术之一［1］，具有很好的发展前景，在现代航空航天领域得到了广泛应用［2-5］。作为一种位置伺服系统，机电作动器可以将伺服控制器的输出信号转化为位移、速度、载荷等物理量，从而实现对控制对象进行位移驱动、速度驱动、载荷驱动的目的［6］。因此，一旦机电作动器发生故障，不仅会对EMA 本身造成危害，还会导致整个系统输出无法正确响应控制指令，对系统的性能及安全造成很大的影响。

目前，EMA 的故障诊断方法主要分为基于解析模型的方法、基于专家知识的方法和基于数据驱动的方法［7］。其中，基于解析模型的方法要求对目标系统进行精确的数学建模，对不同故障模式进行建模仿真分析。由于机电作动器是一种高度非线性的复杂机电系统，因此想要建立精确的EMA数学模型难度很高。基于专家知识的故障诊断方法依赖相关领域专家的专业知识和经验，通过对系统的常见故障模式进行分析，确定其故障机理、影响以及对应的故障特征，建立故障诊断知识库，然而，EMA 关于故障诊断的研究不够充分，难以建立完善的故障诊断知识库，所以排除该方法。基于数据驱动的方法根据系统故障信号提取故障特征，判断其故障类型、程度。近年来，基于人工智能的方法成为数据驱动故障诊断的研究热点。Chirico 等［8］对机电作动器的轴承和滚珠丝杠这两个重要部件的相关故障进行了研究，通过采集振动信号和电流信号，并对其进行故障特征提取，从而获得故障特征集，最后使用贝叶斯分类器对故障特征集进行分类诊断；李璠等［9］研究EMA 电机的直流母线电流信号，进行傅里叶变换，通过研究电流信号频域的特征变化来对EMA 进行在线故障诊断；刘俊等［10］使用集合经验模态分解算法对EMA 的振动信号进行特征提取，分析故障特征来进行故障检测与隔离；田瑶瑶等［11］使用基于数据驱动的故障诊断方法，使用小波包分解进行故障特征提取，使用自组织映射神经网络完成故障模式识别，实现了对EMA卡死、偏差、增益三类故障的研究。

然而，上述研究在故障特征提取方面仅针对单一故障进行，缺乏对有效特征的筛选，导致故障特征之间区分性较差；在故障模式识别算法上迭代优化过慢，训练效率较低，最终使得故障诊断精度受到限制。

本文提出了一种基于集合经验模态分解-学习矢量量化网络（Ensemble Empirical Mode Decomposition，Learning Vector Quantization，EEMD-LVQ）的EMA故障诊断方法，能够有效地对机电作动器的典型故障和故障耦合模式进行检测与隔离。针对EMA的多种故障信号，利用集合经验模态分解（Ensemble Empirical Mode Decomposition，EEMD）算法同步完成故障特征提取，共同构建故障特征向量，并对EEMD算法和LVQ算法进行了优化，利用相关系数对EEMD算法分解结果进行筛选，完成特征降维，同时使用余弦衰减算法来优化LVQ算法的学习率更新部分。

1 基于EEMD的故障特征提取

故障特征提取是进行故障检测与隔离前的重要步骤，主要目的是从采集到的故障信号中提取出能够表征该故障模式的故障特征。机电作动器的故障特征提取过程主要包含：信号处理、特征构建和特征降维。其中，信号处理是指对采集到的仿真信号进行EEMD算法分解，从而生成若干个本征模态函数（Intrinsic Mode Function，IMF）［12］。特征构建是指对EEMD 分解产生的IMF分量，计算出各自的能量值，并进行归一化处理，得到能量特征分布向量［13］。而特征降维则是指针对特征构建环节生成的能量特征分布向量，使用相关系数进行筛选，从中选出合适的IMF分量能量值加以保留，构建最终的故障特征向量输出。

为解决EMD算法中的边缘效应和模式混淆问题，EEMD算法引入了高斯白噪声叠加和结果的集成平均处理。

首先，EEMD算法将原始信号分解为若干个IMF分量和残差［14］。其中，IMF定义如下：

a）在IMF 整个数据序列中，函数的极值点数与穿越零点的数目之差不能超过1；

b）对于IMF 数据序列的任意一点，求出其局部极大值和极小值，分别绘制上包络线和下包络线，得到两条曲线的均值为0。

其次，对所有IMF 分量的能量值进行归一化处理，形成能量特征分布向量。最后，计算各个IMF分量与原始信号的相关系数，并设置适当的阈值，筛选出相关系数较大的IMF分量，将相关系数较大的IMF分量的能量值占比作为故障特征向量的输出。

EEMD算法的具体步骤如下［15］：

a）初始化EEMD 的总体平均次数N和叠加高斯白噪声的幅值系数k，令i=1；其中，N为执行EMD分解的总次数，会影响信号的消噪能力与计算时间；k为叠加的高斯白噪声的幅值系数（高斯白噪声标准差与原始信号标准差的比值），一般取0.1～0.4，k会影响信号的分解精度；i是当前执行EMD分解的次数。

b）向原始信号x(t)叠加高斯白噪声：

式中vi(t)为执行第i次EMD分解时所叠加的高斯白噪声；xi(t)为执行第i次EMD分解时叠加高斯白噪声后的新信号。

c）对xi(t)进行EMD分解：

式中cij(t)为xi(t)的第j个IMF 分量；rn(t)为分解的残差，反映了xi(t)的变化趋势。

d）重复操作步骤b和步骤c，直至i=N。

e）对EMD分解的结果作集成平均处理：

式中cj(t)为原始信号的第j个IMF分量。

f）计算各个IMF分量的能量Ek与总能量E：

式中M为各个IMF分量中的信号点数；ck，m为第k个IMF分量的第m个信号点。

g）求出各频段能量分布，得到能量特征分布向量T0，进行归一化处理：

h）计算出各个IMF 分量与原始信号x(t)的相关系数rj：

式中cj，m为第j个IMF 分量的第m个信号点；xm为原始信号x(t)的第m个信号点。

i）设定阈值，筛选出相关系数超过阈值的IMF分量。

j）使用筛选出的IMF 分量的能量值占比，构建故障特征向量T：

综上，利用EEMD算法对原始信号x(t)进行一系列处理，最终生成故障特征向量Τ。

2 基于LVQ的故障模式识别

在完成对EMA的故障特征提取，得到故障特征向量集合后，就需要选用合适的分类器进行故障模式识别。由于LVQ算法具有低计算复杂性，对噪声和数据不完整性有较强的鲁棒性，适用于小样本问题，分类边界可解释的优势，因此选用LVQ算法作为分类器。

2.1 学习矢量量化网络算法

LVQ算法的结构组成如图1所示。

图1 LVQ算法的结构示意Fig.1 Schematic structure of the LVQ algorithm

由图1可见，LVQ算法由3个主要组成部分构成：输入层、竞争层和输出层［16］。输入层和竞争层间的神经元之间存在完全连接，它们的权值是LVQ神经网络的训练目标。然而，输出层神经元和竞争层神经元之间只有部分连接，竞争层神经元只与一个输出层神经元连接，竞争层与输出层之间的连接权值均为1。

LVQ算法的工作原理为：输入特征向量后，竞争层神经元中最接近输入向量的神经元获胜，成为激活状态，其他神经元值为0。与获胜神经元相连的输出层神经元也被激活，其他神经元值保持0。最终，网络输出一个由1 和0 组成的向量，实现分类功能。在训练过程中，通过调整输入层到竞争层的权值，并参考标记信息进行训练。如果输出与标记一致，判定为正确分类，获胜神经元的权值朝输入方向调整；如果不一致，判定为错误分类，权值朝相反方向调整。LVQ算法的具体步骤为［17］：

a）网络初始化。

将竞争层神经元权值向量的初始值设定为较小的随机数，并确定初始学习率η与训练次数T；其中，竞争层神经元的权值向量为

式中Wj为第j个竞争层神经元的权值向量；ωij为第i个输入层神经元和第j个竞争层神经元之间的权值。

b）输入样本{X，t}。

样本中的输入向量X应该和对应的标记信息t成对出现，且输入向量X的表达式为

c）求解欧式距离。

求出输入向量和权值向量之间的欧式距离：

式中dj为输入向量和第j个竞争层神经元权值向量的欧式距离。

d）找出获胜神经元。

比较所有竞争层神经元的欧式距离，找出欧式距离最小的那个竞争层神经元，将其记为获胜神经元j*。

e）进行权值更新。

对比输入向量X的标记信息t和获胜神经元j*的分类结果，若相同，认为分类正确，此时，获胜神经元j*的权值向量向输入向量的方向移动，即：

反之，如果获胜神经元j*的分类结果和输入向量X的标记信息t不同，则认为分类错误，将获胜神经元j*的权值向量朝输入向量进行反向移动，即：

f）更新学习率η。

g）判断是否达到了设定的训练次数。

若达到设定的训练次数T则结束算法，否则转到步骤b继续训练，直至达到设定的训练次数，方可结束训练。

2.2 LVQ算法的优化

为优化LVQ 算法，Kohonen［18］对LVQ 算法的权值更新部分进行了优化，提高了分类泛化能力。同时，本文还提出了使用余弦衰减算法来进行LVQ的学习率更新，兼顾了训练效率和后期的稳定性。

a）权值更新的优化。

为了提高LVQ算法的分类能力，可以在每次权值更新时同步更新竞争层中的两个神经元的权值。如果在竞争层中有两个神经元最接近输入向量，其中一个对应正确分类，而另一个对应错误分类，并且输入向量位于它们的中位面附近，那么就同时更新这两个神经元的权值。这种方法可以对难以分类的数据进行模式识别，以提高LVQ算法的分类泛化能力。

对此，还需引入窗口的概念，增加了窗口参数α，取值范围为0.2～0.3。窗口的定义为

式中di，dj分别为输入向量到两个竞争层神经元权值向量的欧式距离。

当两个竞神经层神经元i与j属于不同类别，且它们与输入向量的欧式距离之比大于s时，则对i与j的权值向量同时进行调整。如果神经元j*和u*不满足上述两个条件，则只需要对获胜神经元j*进行权值更新，与优化前算法的权值更新方式一致。

b）学习率更新的优化。

为了提高LVQ算法的训练效率和兼顾后期的稳定性，相较于传统的固定学习率方法，采用余弦衰减算法进行学习率更新有收敛速度更快、泛化性能更快的优势。因此，本文使用余弦衰减算法对LVQ算法的学习率更新部分进行了优化。余弦衰减算法的表达式为

式中k为当前训练的次数；η(0)为初始学习率；α为最小学习率系数；ηmin为最小学习率；km为衰减步数，即从初始学习率衰减到最小学习率需要的训练次数。

3 试验验证

利用真实EMA 在正常状态和不同故障状态下的信号数据，对本文提出的故障特征提取算法和故障模式识别算法进行验证。机电作动器故障诊断试验验证的流程如图2所示。

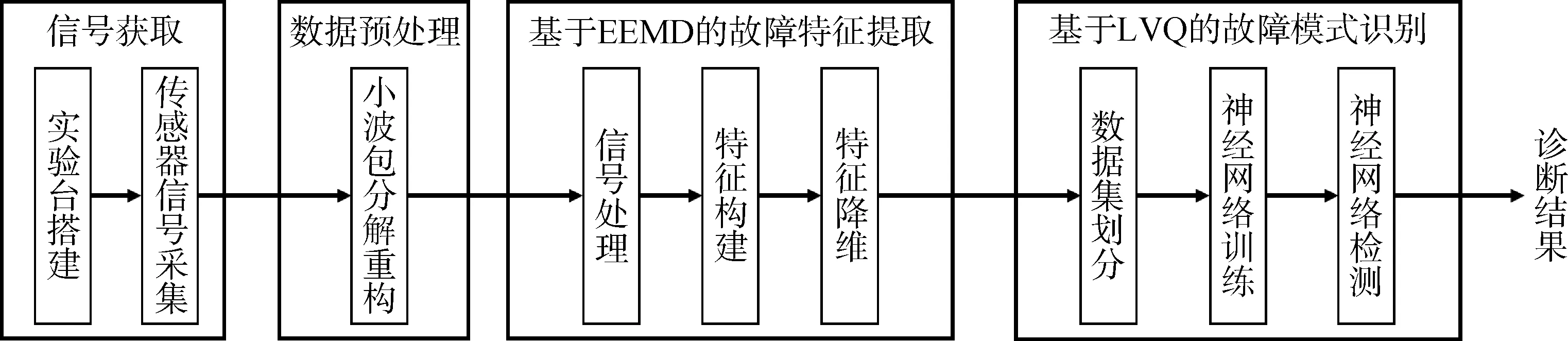
图2 基于EEMD-LVQ的EMA故障诊断试验验证流程Fig.2 EEMD-LVQ based EMA fault diagnosis test validation process

3.1 数据获取和预处理

本文使用EMA故障试验数据进行试验验证，分别对EMA正常状态和旋变传感器偏置故障进行试验，将传感器采集到的故障信号输入到计算机中，作为试验数据进行储存。试验数据的总时长为5 min，采样周期是2 ms。试验数据主要包含：电机d轴电流信号、电机q轴电流信号、电机转速信号和舵面输出信号。

对于EMA故障信号来说，其故障特征往往反映在高频部分，因此使用小波变换来去除噪声会导致故障特征丢失。为避免这一问题的发生，本文使用小波包分解重构算法来对EMA 故障试验数据进行降噪预处理［19］。

3.2 基于EEMD的故障特征提取算法验证

完成了数据预处理后，需要对试验重构信号进行故障特征提取。将重构后的试验信号拆分为30 份，每份数据时长10 s。因此得到了EMA 正常状态、旋变传感器偏置故障这两种模式下各30组试验数据。

在数字仿真软件中实现EEMD算法，设定EEMD算法的相关参数：总体平均次数N=100，高斯白噪声的幅值系数k=0.25。对EMA正常状态、旋变传感器偏置故障的试验数据使用EEMD算法进行故障特征提取，得到相对应的故障特征向量，下面以电机d轴电流信号为例介绍EEMD分解和相关性分析过程。

对EMA试验信号中的d轴电流信号，进行EEMD算法分解，完成信号处理后，可以获得11 个IMF 分量和残差。计算出这些IMF分量的能量值并进行归一化处理，可以明确d轴电流信号的频率组成以及各频率分量的大小情况。最终，可以得到EMA 的正常状态和旋变传感器偏置故障模式下d轴电流信号的能量特征分布向量，如图3所示。

图3 d轴电流信号EEMD分解结果Fig.3 EEMD decomposition results of d-axis current signal

图3 中，对于电机d轴电流信号，机电作动器的正常状态和旋变传感器偏置故障之间，能量特征分布向量具有比较好的区分性。

在完成了对EMA 试验信号的信号处理和特征构建，获得能量特征分布向量后，就需要对其进行特征降维，利用相关系数筛选出合适的IMF分量，保留其能量值占比，构建故障特征向量。

求出电机d轴电流信号的各个本征模态分量与原始试验信号之间的相关系数，并设置合适的阈值。选择相关系数标准差作为阈值，对IMF 分量进行筛选。电机d轴电流信号的相关性分析结果如图4所示。

图4 d轴电流信号相关性分析结果Fig.4 d-axis current signal correlation analysis results

图4中红色水平线表示EMA的d轴电流信号相关系数的阈值。筛选出相关系数超过阈值的IMF 分量，并求出机电作动器两种模式下所筛选出的相同部分加以保留，作为EMA电机d轴电流信号相关性系数筛选的结果输出。

同理，对EMA电机q轴电流信号、电机转速信号、舵面输出信号进行EEMD分解和相关性分析，选取出相关系数大于阈值且区分性较好的IMF分量。将筛选出的IMF分量的能量值占比作为特征值，构造故障特征向量。同时，还要向故障特征向量中添加标记信息，最终得到已标记的故障特征向量集，如表1所示。由表1可以看出，机电作动器的正常状态和旋变传感器偏置故障之间，故障特征向量具有很好的区分性。

表1 EMA试验数据故障特征向量集的一个样本Tab.1 A sample of the set of fault eigenvectors for EMA test data

3.3 基于LVQ的故障模式识别算法验证

在数字仿真软件中实现LVQ 算法，设定LVQ 参数：初始学习率η=0.01，最大训练次数T=100，余弦衰减算法的衰减步数km=50，最小学习率系数α=0.01。

针对LVQ算法，输入层有9个神经元，竞争层有5 个神经元，输出层有2 个神经元。将之前经过EEMD处理提取的故障特征向量集作为输入样本，并进行标记。将输入样本随机排列，按照3 ∶ 2的比例划分为训练集和测试集。训练集包含36 个向量，测试集包含24 个向量。将训练样本输入LVQ 算法进行训练，最终得到已训练完成权值向量的LVQ神经网络。接着，利用测试样本进行检测，得到故障诊断结果。训练误差收敛曲线如图5所示。

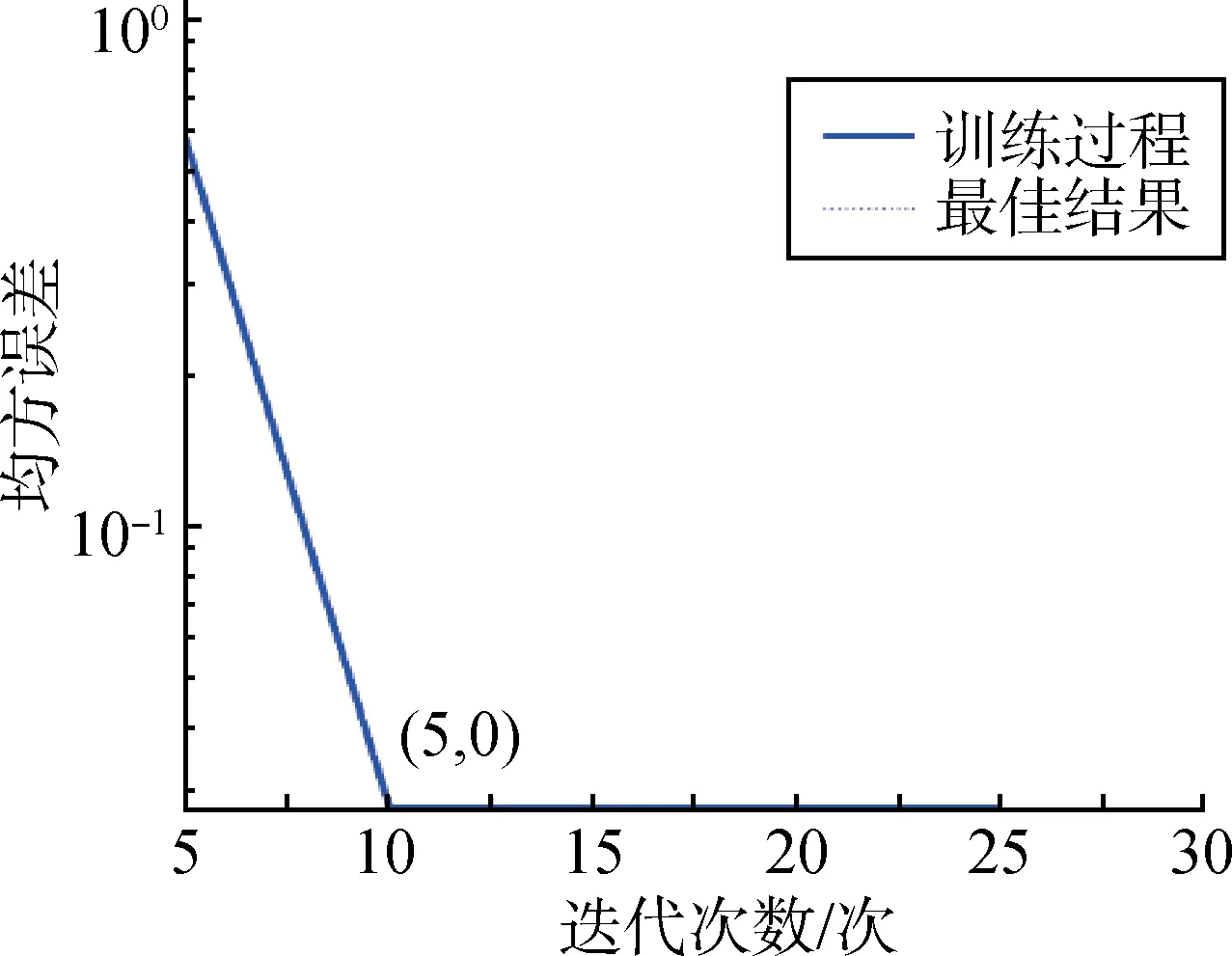
图5 EEMD-LVQ算法的训练误差收敛曲线Fig.5 Training error curves for the EEMD-LVQ algorithm

由图5可以看出，LVQ算法的训练误差收敛速度非常快，且最终误差为0。因此，LVQ 算法的故障诊断结果验证了基于EEMD-LVQ 的故障诊断方法的准确性与优越性。

LVQ算法对测试集中各类故障特征向量的诊断准确率如表2所示。

表2 EEMD-LVQ算法的故障诊断准确率Tab.2 Fault diagnosis accuracy of EEMD-LVQ algorithm

由表2可以看出，LVQ算法对检测集中正常状态和旋变传感器偏置故障的诊断准确率均为100%。因此，可以证明基于EEMD-LVQ 的故障诊断系统能够对机电作动器的正常状态、旋变传感器偏置故障做出准确判断，完成故障检测与隔离。

3.4 对比分析

为了评估EEMD-LVQ 算法在故障特征提取方面的优越性，将其与小波分解-LVQ 故障诊断方法进行对比分析。通过比较两种方法的故障诊断准确率和训练误差收敛曲线，可以看出EEMD-LVQ 算法相对于小波分解-LVQ算法的优势。小波分解-LVQ的训练误差收敛曲线结果如图6所示。

图6 小波分解-LVQ算法的训练误差收敛曲线Fig.6 Training error curves for the wavelet decomposition-LVQ algorithm

由图6可以看出，小波分解-LVQ故障诊断方法的训练误差收敛速度很快，但是其最终误差比较大。通过比较图5和图6中的训练误差收敛曲线的情况，可以证明EEMD-LVQ故障诊断方法的最终误差较小，具有更好的稳定性。其中，故障诊断准确率的结果比较如表3所示。由表3可以看出，小波分解-LVQ故障诊断方法对检测样本的诊断准确率为79.17%，而EEMDLVQ故障诊断方法对检测样本的诊断准确率为100%。因此证明了EEMD-LVQ 故障诊断方法具有更强的故障识别能力，对EMA故障诊断的效果更好。

表3 两种方法故障诊断准确率比较Tab.3 Comparison of fault diagnosis accuracy between the two methods

由于EMA 是一个多变量、强耦合的复杂系统，其故障模式在多个信号中都有反映。为了提高故障诊断的准确性，本文同时提取了电机的q轴电流、d轴电流、转速和舵面输出信号的故障特征，并构建了故障特征向量。

图7为采用EEMD-LVQ算法提取舵面输出信号的训练误差收敛曲线，可见针对单一故障信号进行处理方法的训练误差收敛速度较慢，且最终误差很大。通过比较图5 和图7 中的训练误差收敛曲线的情况，可以证明针对多种故障信号进行同步处理方法具有更高的训练效率和更好的稳定性。

图7 只提取舵面输出信号的训练误差收敛曲线Fig.7 Training error curves for extracting only the rudder output signal

针对单一信号和多种故障进行故障诊断准确率的比较如表4所示。由表4可以看出，针对EMA单一信号进行故障诊断方法的诊断准确率为58.33%，而针对4 种故障信号进行故障诊断方法的诊断准确率为100%。因此证明了对多种故障信号进行同步处理方法具有更强的故障识别能力，对EMA 故障诊断的效果更好。

表4 单一故障信号和多种故障信号的故障诊断准确率比较Tab.4 Comparison of fault diagnosis accuracy between single and multiple fault signals

4 结束语

本文以机电作动器为研究对象，提出了基于EEMD-LVQ 的故障诊断算法，并对EMA 的故障诊断展开了研究。首先，使用EEMD 算法对EMA 信号进行同步分解，获取IMF分量，并计算出各个IMF分量的能量值占比，构建能量特征分布向量；其次，使用相关系数对IMF分量进行筛选，完成特征降维，获取故障特征向量集，并添加标记；最后，利用故障特征向量集对LVQ神经网络完成训练与检测，获得故障诊断结果。为验证算法的有效性，本文使用了实际试验数据进行了验证，证明了本文提出的EEMD-LVQ 算法与传统算法相比收敛速度快、稳定性强，且多信号同步特征提取相比单一信号特征提取具有更强的故障识别能力。