面向灾害蔓延仿真的元胞自动机通用模型

王威, 陈勃阳, 刘朝峰, 王志涛*

(1.北京工业大学城市建设学部, 北京 100124; 2. 河北工业大学土木与交通学院, 天津 300401)

进入20世纪以来,全球范围内海啸、洪水、干旱、飓风和地震等自然灾害的频率和强度日益加剧,正不断地威胁着人类社会的生存安全。自然灾害数据表明,人类社会正遭受着自然灾害越来越严峻的威胁,损失也越来越巨大[1]。然而,由于灾害时空动态蔓延复杂且后果严重、危险性大,很难进行实验研究,并且受限于实验方案的安全性,即使进行灾害实验也很难证明数据的可靠性。灾害模拟仿真通过计算机数值模拟避免了灾害实验遇到的问题,不仅可以研究灾害触发→叠加→耦合→累积演化的蔓延机理,还可以对灾害进行动态预测。元胞自动机(cellular automata, CA)是一种时间、空间、状态都离散,空间相互作用和时间因果关系都为局部的网格动力学模型[2],在灾害模拟、应急疏散等[3-4]领域有广泛应用。元胞自动机应用于模拟森林火灾蔓延已经取得了很多成果[5-6],在三维森林火灾模拟方面,张全文等[7]将地理信息系统(geographic information system,GIS)三维可视化和元胞自动机原理相结合,模拟了“3·29”温泉镇火灾在三维空间中的动态蔓延变化。对于城市火灾蔓延,日本学者Ohgai等[8]在2007年提出了日本城市社区火灾蔓延的元胞自动机模型,首次将元胞自动机成功应用到城市火灾蔓延模拟领域;对于地下矿火蔓延,黄光球等[9]提出了一个基于粒子系统理论的地下矿巷道系统中火灾蔓延的元胞自动机模型。在拥挤踩踏仿真方面,张磊等[10]以安全出口前拱形拥挤疏散行人流为研究对象,建立了基于拥挤力的拥挤致伤元胞自动机模型;岳昊等[11]提出了基于行人相互作用力的步行设施内行人流拥挤踩踏的元胞自动机模型。在滑坡运动时空动态模拟领域,意大利学者Avolio等[12]在2000年首次提出了SCIDDICA模型用于模拟滑坡、泥石流等地质灾害发展过程。对于洪水蔓延,蔡新等[13]构建了基于体积法思想的洪水淹没模拟元胞自动机模型;刘恒[14]采用二维圣维南方程和基于数字高程模型(digital elevation model,DEM)的单元栅格大伙房产流模型建立了洪水演进元胞自动机模型。对于疾病传播,于鑫等[15]提出了一种基于随机行走的流行病传播与控制元胞自动机模型;谭欣欣等[16]提出了一种基于随机行走的考虑个体异质性和移动性的SEIR(susceptible-exposed-infected-recovered)传染病传播元胞自动机模型。对于恐怖袭击,曹淑超等[17]建立了考虑恐怖袭击模式的行人疏散元胞自动机模型,研究了不同袭击模式和疏散场景下的疏散时间、人员伤亡和位置分布。

综上所述,目前虽然许多灾害都采用了元胞自动机进行动态仿真模拟,但尚无一种通用的建模方法。基于此,现提出一种面向灾害蔓延仿真的元胞自动机通用模型,用于现有模型的改进和新模型的建立。首先建立灾害蔓延的理论模型,然后将理论模型的时间和空间离散,之后寻找离散空间单元的状态变化规则,并确定一个时间步长内空间单元的遍历次序,以及不同状态的计算次序,最后,按照元胞自动机的结构将每个时间步的计算连接起来,得到按时间步循环更新状态的灾害蔓延仿真元胞自动机模型。

1 灾害蔓延仿真通用模型

由于灾害本身的发生和发展往往是一系列相关事件,而概率型元胞自动机正是按特定规则演化的随机动态系统,对因果关系、函数关系并不确定的各种各样灾害事件来说具有强大的描述能力。而对于某些已经被人类深入研究过的灾害,其与状态改变有关的函数和参数已经确定,可根据已有的灾害数学模型再建立一个时空离散的、自底向上计算的数学模型,并据此构建元胞自动机模型。

1.1 模型构建基本思路

步骤1选取具有代表性的变量作为建模初始变量。灾害在空间中扩展时,会将正常区域纳入灾害区域,灾害在空间中消退时,灾害区域会变成复原区域,同时,灾害区域内部也会随时间产生恶化或退化等变化。在灾害演化过程中,会有许多变量随之变化,但为简化计算模型,只需选取具有代表性的变量作为建模初始变量。例如,火灾中某一元胞是否着火以及着火后的温度或燃烧阶段,洪水中某一元胞的水深或流速等。

步骤2建立初始变量的计算方法。在取得建模初始变量后,根据现有理论或由观测数据得到的经验公式等,建立在离散时空中的初始变量的自底向上的计算方法。在初始变量的计算函数中,会包含很多参数,这些参数和初始变量一起都将作为模型的灾害量。

步骤3建立灾害量中变量的计算方法。在取得灾害量后,根据现有理论或由观测数据得到的经验公式等建立在离散时空中的灾害量中变量的自底向上的计算方法,其中新加入的参数作为模型的灾害量。

步骤4重复步骤3,直至模型不再加入新的灾害变量为止。

步骤5最后,确定所建立的多自变量、多参变量且多步骤的大型函数中,所有变量在一个离散时间步内的计算次序。

1.2 灾害元胞自动机属性集合

灾害发展变化时不同灾害变量计算过程相似,在划分好元胞空间并确定了边界条件后,每一种灾害都可分为4个集合:灾害量集S1、时空邻域集S2、判定规则集S3、更新规则集S4,如表1所示。

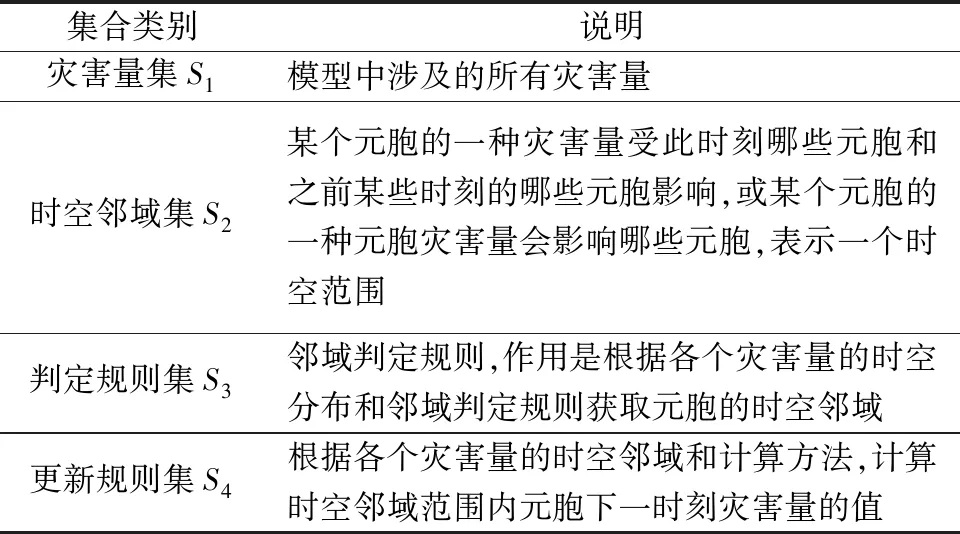
表1 灾害属性集合Table 1 Disaster attribute set

1.3 模型参数解析

依据CA编程方式,将表1中的4类集合、元胞空间和边界条件重新组合成一个程序整体。只需输入数据,就可计算在时间限内各个灾害变量的时空变化。模型中存在许多随时间变化的参数,每1种随时间变化的参数都可采取如下方式计算。

(1)

(2)

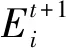
(3)

(4)

上述为在1个时间步中1个时变变量的更新方法。当所有时变变量都更新完成后,进入下1个时间步循环,直至规定的条件达成。

为进一步详细阐述本模型的建模步骤,以城市火灾蔓延的元胞自动机模型为例进行解析。

2 城市火灾蔓延A.Ohgai模型改进

2.1 模型参数与火灾蔓延规则

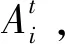
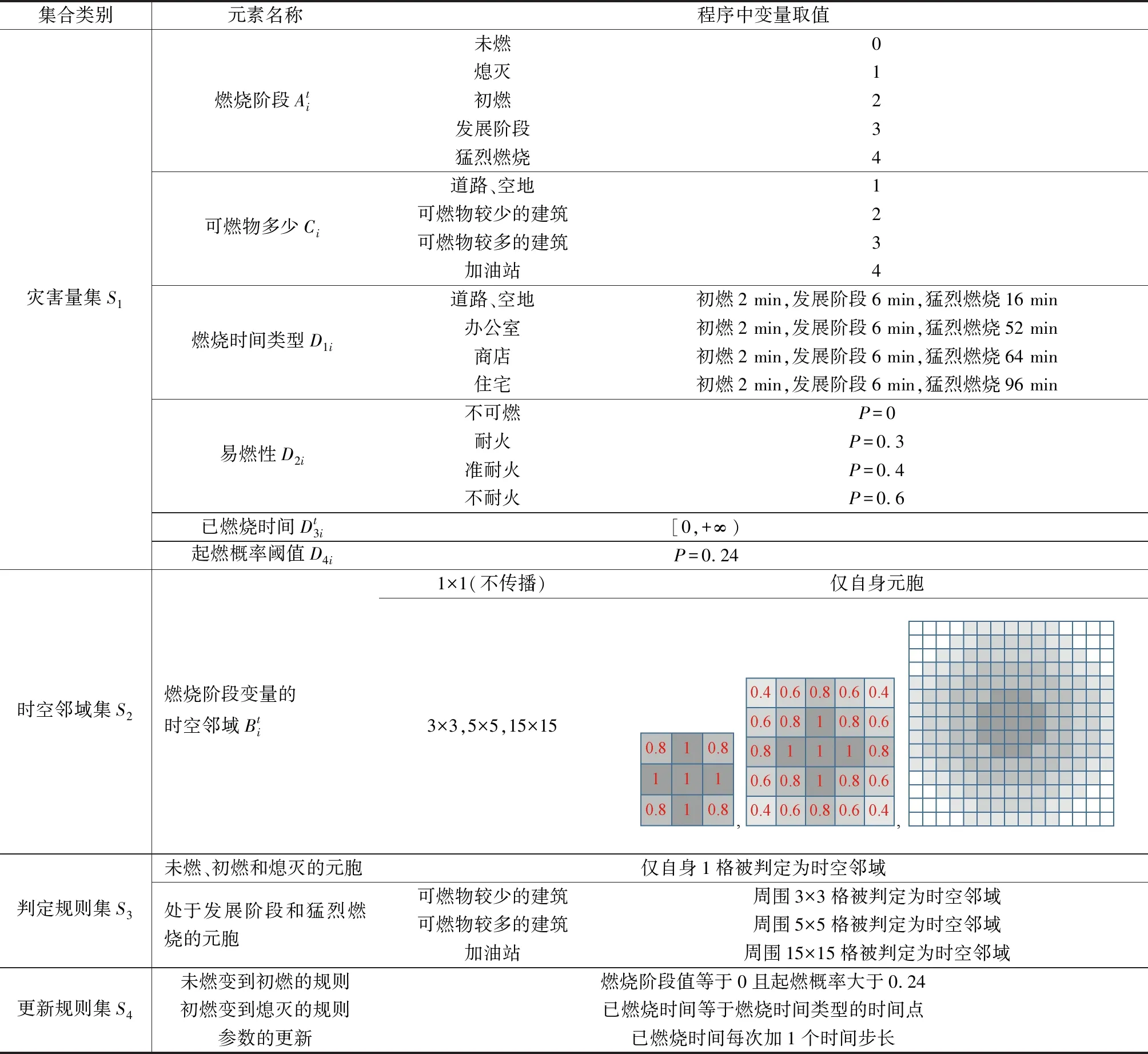
表2 改进A.Ohgai的城市火灾蔓延模型属性集合Table 2 Attribute set of the improved urban fire spread model of A.Ohgai

为区分不同可燃物燃烧后的火灾蔓延能力,采用邻域可变型元胞自动机,当建筑物的燃烧物较多时,这类建筑物的位置处的元胞邻域范围更大。根据Jirou等[20]提出的火向下风向传播的极限距离公式计算,公式为

DT=1.15(5+0.5v)

(5)

式(5)中:v为风速,m/s;DT为火势传播距离极限,m。当风速v=0 m/s时,DT=5.75 m。为保守起见,将燃烧物较少的建筑的邻域范围取2.4 m,而燃烧物较多的建筑的邻域范围取4.8 m。模型元胞自动机的元胞大小为2.4 m×2.4 m,即上述两类建筑物的火灾时空邻域的范围分别为3×3格、5×5格。2021年6月14日,俄罗斯新西伯利亚市一座加油站爆炸,过火面积约1 200 m2,据此,将加油站位置处的元胞时空邻域范围取为36 m×36 m,即15格×15格。模型与时空邻域判定有关的参数集只有按可燃物分类的建筑类型这一个参数,在程序中,与时空邻域判定有关的参数集可表示为

Ci∈{1,2,3,4},Ci∈S1

(6)

式(6)中:1表示燃烧物较多的建筑;2表示燃烧物较少的建筑;3表示加油站;4表示道路空地。

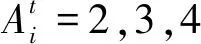
元胞起燃概率的计算方法如下。

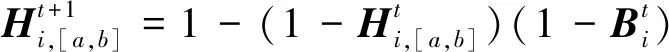
(7)

式(7)中:Ht+1为下一时刻的似起燃概率矩阵。

步骤3计算下一时刻的起燃概率。预定义一个和元胞空间同维度的矩阵SP,SP中的值为对应位置元胞的易燃概率D2i,则有

Ht+1=Ht+1SP

(8)

式(8)中:Ht+1为t+1时刻所有元胞的起燃概率。

2.2 实例仿真模拟

选取北京市白塔寺周边1.2 km×1.2 km范围为例,将建筑平面染色,获得建筑物易燃性的染色图(图1);根据实地调研,依据燃烧物类型及数量染色,获得建筑物的染色图(图2);对建筑物燃烧时间的分类,依据燃烧时间类型将建筑平面染色,获得建筑物的染色图(图3)。

图1 易燃性Fig.1 Inflammability

计算机程序结构如下。

步骤1采用MATLAB中的imread()命令读取三张染色图图1、图2、图3,用imresize()命令将三张图划分为m×n的网格,再用rgb2ind()命令将染色图转化为索引图。

步骤2根据索引图数据,对易燃概率矩阵SP、可燃物多少矩阵V、燃烧时间类型矩阵FT赋予初值。

步骤3初始化燃烧时间记录矩阵HT,初始化火灾状态矩阵H,在初燃的位置处,H初始化值为2。

步骤4遍历所有元胞,当遇到元胞状态H初始化值大于2时,计算此处的时空邻域。

步骤5根据计算所得的所有时空邻域,计算下一时刻所有元胞的起燃概率。

步骤6当未燃元胞的起燃概率大于0.24时,未燃元胞变为初燃状态元胞。当初燃状态元胞的已燃烧时间达到元胞燃烧时间类型规定的转变时间点时,元胞进入发展阶段状态。当发展阶段状态元胞的已燃烧时间达到元胞燃烧时间类型规定的转变时间点时,元胞进入猛烈燃烧阶段状态。当猛烈燃烧阶段状态元胞的已燃烧时间达到元胞燃烧时间类型规定的转变时间点时,元胞进入熄灭状态。

步骤7更新元胞处于已燃状态的时间矩阵HT。

步骤8将元胞染色并显示图像。

步骤9回到步骤4,进行循环。

进行多情景城市火灾蔓延仿真分析。情景一:假定居民区着火,如图4所示;情景二:假设即将修建一座加油站,加油站着火,如图5所示。

图4 居民区着火蔓延情景模拟Fig.4 Simulation of fire spread in residential area

可以看出,本文模型可以实时计算不考虑救援力量情况下的火灾的范围及状态,居民区着火时火灾的蔓延速度比较平稳,加油站着火时能够瞬间影响较大范围的可燃物。本文模型将邻域范围作为变量并可取不同值,解决了元胞自动机模型应用于灾害模拟时无法根据实时的环境变化灵活改变灾害蔓延方向、距离、速度的问题。但火灾模型的结构和计算过程比较简单,有待进一步改进,同时,模型中的参数取值也需进一步研究。

3 结论

城市火灾蔓延仿真模型能够快速展现真实的火蔓延过程,体现了元胞自动机的火灾仿真能力。所采用多层的、邻域可变的非标准元胞自动机通用模型的应用较为简便。本文模型也可扩展用于离散时空中多种灾害的自底向上建模的仿真模拟,即灾害变量的改变描述是灾害在时间尺度上的变化,灾害的时空邻域描述的是灾害在空间尺度中的变化范围,这方面还需进一步研究。