跨座式单轨车轨耦合系统振动信号采集频率分析

2023-12-15韩建棒申彦利刘焕举

科学技术与工程 2023年33期

韩建棒, 申彦利,2,3*, 刘焕举

(1.河北工程大学土木工程学院, 邯郸 056038; 2. 河北省装配式结构技术创新中心, 邯郸 056038;3. 河北工程大学新型单轨交通体系工程研究中心, 邯郸 056038)

对于跨座式单轨车轨耦合系统中,常于轨道梁跨中底部和车体重心位置放置振动加速度传感器采集数据,经处理得到轨道梁跨中振动加速度和行车平稳性指标值来反映轨道梁与车辆的振动响应。实际的车轨耦合振动信号具有连续、随机且频率分布广的特点,实际信号的奈奎斯特频率无法确定,而通过振动加速度传感器采集得到的是实际信号抽取得的离散信号[1]。采集频率低会使大量实际高频信号混入低频信号造成信号混叠以及达不到幅值精度要求而导致测量误差,采集信号过大则会增大计算时长,占用计算资源。因此,对跨座式单轨车轨耦合系统振动信号采集频率分析得出合适的采集频率范围具有重要的学术和工程价值。

在《机车车辆动力学性能评定及试验鉴定规范》(GB/T 5599—2019)[2]中规定,用于评价行车舒适度的铁道机车车辆振动加速度传感器工作频率需为0～100 Hz。刘汉夫[3]对铁路桥梁的横向动力响应的测试进行分析,提出横向加速度信号采集与分析的若干问题,认为铁路桥梁横向加速度信号的采集应保证信号不混叠和有效频段加速度的幅值精度。对大跨径高铁桥梁动力响应信号的采集,在工程上常采用所关注最高阶频率的10倍作为采集频率,且先用较高采样频率对信号进行侦测[4]。在跨座式单轨车轨耦合系统振动信号采集与处理中,常参考铁路相关规范与研究成果。试验者在跨座式单轨车轨耦合系统振动信号采集中,车辆与轨道梁信号常用采集频率范围分别为50～100 Hz和1～10 kHz[5-8],理论上来说,采样频率越高,采样信号越接近于真实信号,但同时也会增加计算时长,占用计算资源。对大多跨座式轨道梁所关注的最高阶频率在5～20 Hz[9-10],若参考工程常用方法,采样频率偏低使采集数据达不到幅值精度、发生信号混叠,使采样数据经处理后的结果可信度降低;而侦测选用的“较高频率”没有给出大致范围,使侦测频率的选取有一定的难度。跨座式轨道梁多采用钢筋混凝土梁,截面形式与跨度差别较小,车桥耦合振动响应真实信号的频率范围相似,对单轨车辆与轨道梁振动响应信号采集频率范围的探究具有重要学术与工程价值。

现利用有限元软件建立跨座式单轨车轨耦合系统,在不同车速工况下设置多组采样频率对车辆与轨道梁进行振动信号采集,将采集数据经处理得出的车辆与轨道梁振动响应结果进行分析,探究减少信号混叠、满足幅值精度要求的跨座式单轨车轨耦合系统振动信号采集频率范围,以期为跨座式单轨车轨耦合振动响应信号采集频率的选取提供参考依据。

1 跨座式单轨车轨耦合系统模型

1.1 车辆与轮轨接触模型

研究采用跨座式宽轮距单轨车辆,因该车型的相关参数的测试数据较少,且与重庆跨座式单轨车辆型式相近,故根据车辆测试数据及借鉴相关车型来取用单轨车辆参数[11-14],车辆系统关键参数如表1所示。

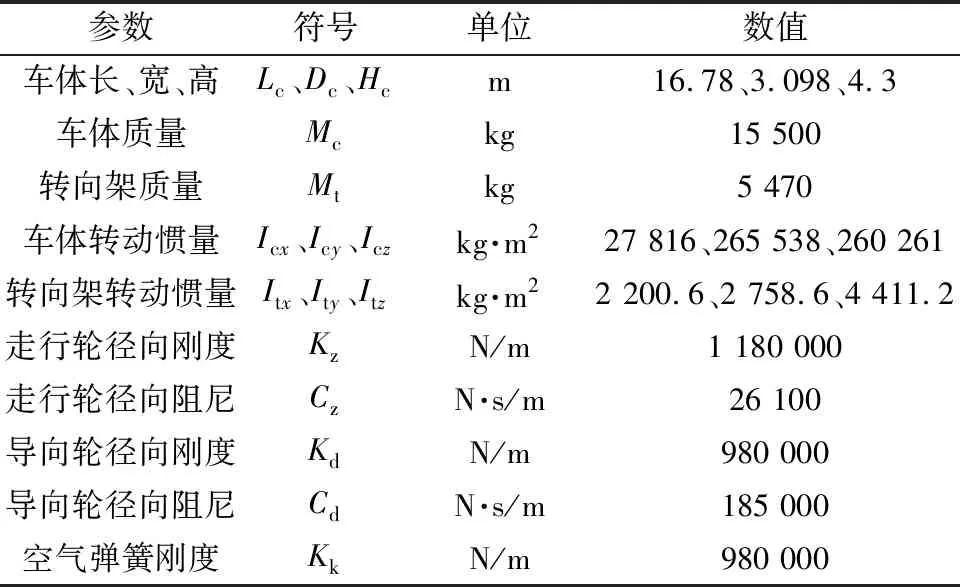
表1 单轨车辆参数Table 1 Monorail vehicle parameters

将车辆离散为车体和转向架等刚体部件,每个部件考虑摇头、侧滚、横摆、沉浮、点头5个自由度,即单节共计15个自由度。在模型建立中对力学元件进行简化,将空气弹簧和减震器看作弹簧阻尼连接,车辆各部件对称设置。车辆运行时沿轨道梁保持轮轨始终接触的匀速行驶,不考虑电机振动对车轨耦合系统振动响应的影响。单轨车辆空间模型如图1所示。

Ψc、Φc、Yc、Zc、Ψt、Φt、Yt、Zt分别为车体及转向架的摇头、侧滚、横摆、沉浮自由度;Kk、Ck、Kj、Cj分别为空气弹簧和减震器的刚度与阻尼图1 单轨车辆空间模型Fig.1 Space model of monorail vehicle

由车辆动力学理论得出单轨车辆振动平衡方程为

(1)

式(1)中:v为下标,指单轨车辆;b为下标,指轨道梁;M、C、K分别为车辆模型的质量、阻尼及刚度矩阵;Z为单轨车辆振动位移向量;Fvg为单轨车辆自身荷载向量;Fvb为轨道梁对单轨车辆作用力列向量。

单轨车辆轮胎力学特性复杂,一般情况下,当轮胎胎压一定时,轮胎荷载与其发生的微小变形可近似为呈线性相关,故对单轨车辆充气式橡胶轮胎的模拟可简化为通过刚度与阻尼恒定且各向相同的弹簧连接器与转向架并联,即采用“线性化点接触式”轮胎模型[15-17],如图2所示。

M为轮胎质量;k、c分别为轮胎径向刚度和阻尼图2 “点接触式”轮胎模型Fig.2 Point contact tire model

跨座式单轨的轮胎和轨道梁接触与公路车辆与路面接触相似,故橡胶轮胎与轨道梁接触的顺桥向和横桥向摩擦因数均取0.25,法向接触根据Hertz接触理论[18],将其看作圆柱体与弹性半空间体的接触。

(2)

式(2)中:F为轮轨接触力;E为路面材料弹性模量;μ为路面材料泊松比;L为轮轨接触宽度;d为轮胎压入深度;p0为轮轨间最大压应力;R为橡胶轮胎半径。

通过轮轨接触力计算得到轮轨间最大压应力和对应的橡胶轮胎压入深度,将两个参数输入有限元分析软件作为轮轨间相互作用接触条件,利用轮胎与轨道梁的相互接触来交换信息和传递数据以实现车桥耦合。

1.2 轨道梁与路面不平度模型

试验采用的轨道梁为跨座式单轨交通系统常用的计算跨径25 m的等截面混凝土简支梁,支座设置宽度为0.8 m。为适用于跨座式宽轮距单轨车辆,轨道梁顶部宽度为1.25 m,底部宽1.1 m。为简化计算,将轨道梁按照毛截面惯性矩进行截面换算,混凝土泊松比为0.2,弹性模量取3.96×104MPa,密度为2.55×103kg/m3,阻尼比设为0.015,轨道梁截面图如图3所示。

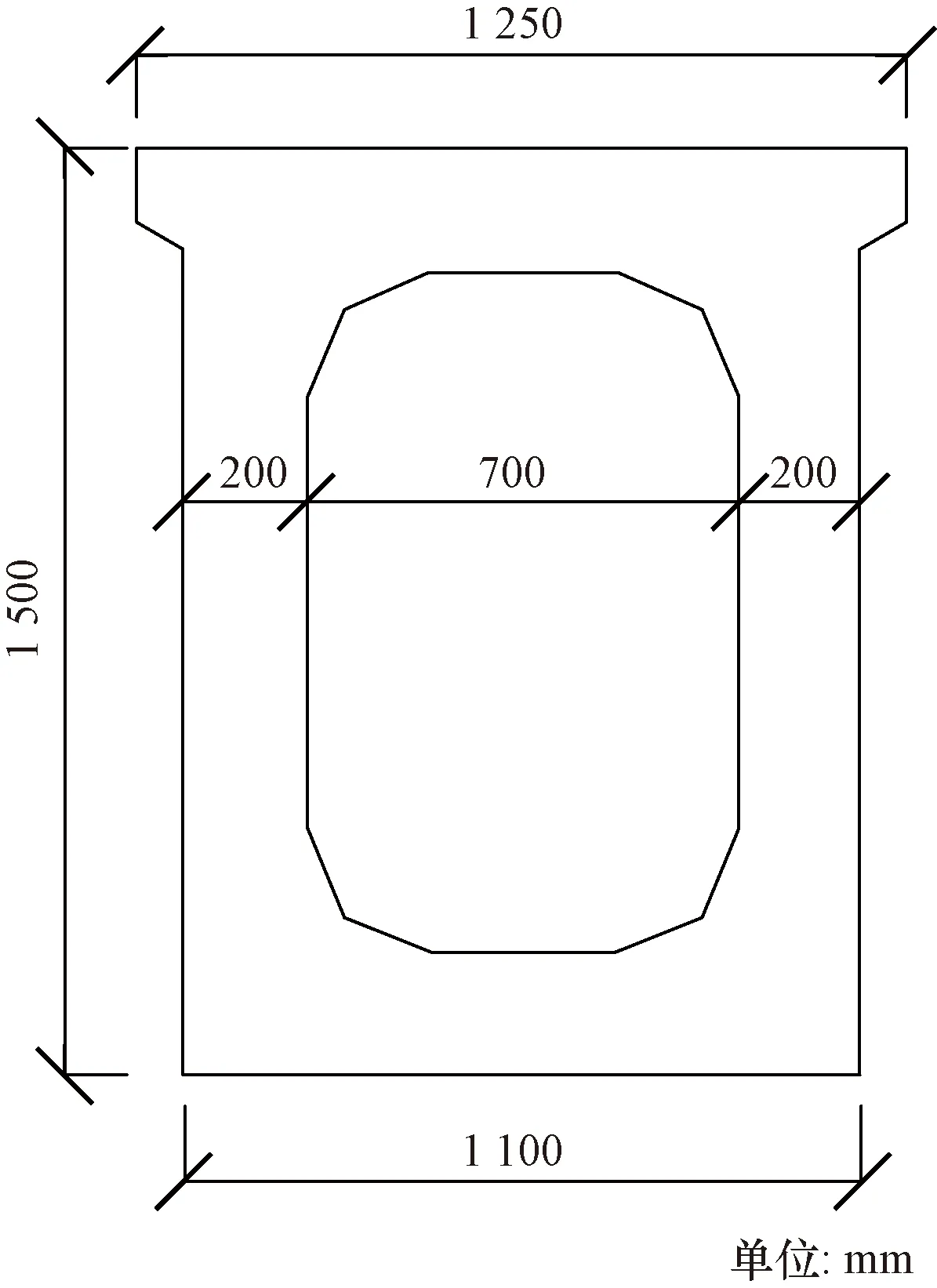
图3 轨道梁截面图Fig.3 Section of track beam

通过有限元法以中性轴算法进行网格划分,将轨道梁离散化处理,每节点具有6个自由度,得到轨道梁振动平衡方程为

(3)

式(3)中;M、C、K为轨道梁模型的质量、阻尼及刚度矩阵;Z为轨道梁振动位移向量;Fbv为单轨车辆对轨道梁作用力列向量。

将车辆振动平衡方程与轨道梁振动平衡方程联立分析知,同一工况下,即车速相同时,车辆及轨道梁质量、阻尼、刚度矩阵始终不变,则振动位移及作用力列向量也保持不变,即在该工况下车轨耦合振动响应不变。在此次求解中车辆与轨道梁时程曲线的真实信号一定,可通过设置多组不同信号采样频率,得到减少信号混叠、具有一定幅值精度且缩短计算时长、节省计算资源的采样频率范围。

车桥耦合系统振动的激励主要来自路面不平度的激励。考虑到当前无适用于跨座式单轨交通系统的路面不平度谱,且单轨车辆通过橡胶轮胎在轨道梁上的行驶更接近于公路车辆在路面上行驶,故选用公路路面不平度作为轨道梁对单轨车辆在运行中的路面不平度激励。根据《机械振动道路路面谱测量数据报告》(GB/T 7031—2005)[19]规定,采用空间功率谱密度函数表达式作为路面不平度的模拟标准,表达式为

(4)

式(4)中:Gd(n0)为路面不平度系数,m3;n为空间频率,m-1;n0为空间参考频率,0.1 m-1;ω为频率指数,取值2。

根据式(4)与文献[20]进行MATLAB程序编写,将路面看作由多条频率与波长均不相同的正弦波相互叠加而成,通过傅里叶变换将众多正弦波叠加并转换为路面不平度高程坐标,将各个路面不平度高程坐标值导入轨道梁模型。考虑到轨道梁多采用工厂预制,对轨道梁制造环节的误差控制较为严格,故试验轨道梁走行面及导向面的路面不平度均采用A级路面。路面不平度函数曲线图如图4所示。

图4 路面不平度函数图Fig.4 Graph of road roughness function

2 车轨耦合系统振动响应结果分析

采用车辆行车平稳性来反映车辆振动响应,根据《机车车辆动力学性能评定及试验鉴定规范》(GB 5599—2019)规定及相关文献[21],将车辆振动时程曲线按频率分组,计算每组的行车平稳性指标Wi,根据每组车辆平稳性指标Wi计算整个时程曲线的行车平稳性指标W,公式如下。

(5)

(6)

式中:Wi为第i组频率对应的行车平稳性指标值;A为车体振动加速度,m/s2;f为车体振动加速度频率,Hz;F(f)为频率修正系数;n为整个时程曲线按频率分组总数。

将计算得到的车辆行车平稳性指标值根据规范要求的行车平稳性评定等级进行评价,行车平稳性评定等级如表2所示。

表2 行车平稳性评定等级Table 2 Ride stability rating grade

由采样得车辆自上桥到出桥过程的轨道梁跨中振动时程曲线,经40 Hz低通滤波得到跨中振动加速度最大值来反映轨道梁动力响应。

2.1 信号采集频率对车辆响应的影响

车辆振动信号的采集点置于车体重心,设置车速v为30、60、90 km/h共3种工况,车辆有轮胎及减震器、空气弹簧等一系悬挂用于减振,因此车辆振动信号采集频率探究范围选用20～800 Hz。通过数据采集,得到3种工况下各信号采集频率的车辆振动时程曲线,图5即车速60 km/h时,信号采集频率为20 Hz和200 Hz下的车辆振动加速度时程曲线对比图。观察对比图可知,采样频率200 Hz比20 Hz的时程曲线能够捕捉更多样本,使车体振动时程曲线能更准确地表达。

图5 20 Hz和200 Hz采样频率下的车体振动加速度时程曲线对比Fig.5 Comparison of vehicle body vibration acceleration time history curves at the sampling frequency of 20 Hz and 200 Hz

将车辆振动时程曲线进行频率分组,根据式(5)、式(6)计算得行车平稳性指标,得到不同车速下车辆振动响应随信号采集频率变化的趋势如图6所示。

图6 不同车速下车辆行车平稳性随信号采集频率变化趋势Fig.6 The ride stability of vehicles at different speeds varies with the signal acquisition frequency

由图6可以看出,在行车平稳性指标处于稳定阶段时,车辆垂向平稳性指标随着车速增加而增大,横向平稳性指标随着车速从30 km/h提升至60 km/h时略微上升,而后车速提高到90 km/h时横向平稳性指标有所下降;在行车平稳性趋于稳定的200～800 Hz采集频率区段,车速在30～60 km/h时,垂向与竖向行车平稳性指标最大差值分别为0.23和0.19,因此,车速对垂向行车平稳性的影响大于对横向平稳性的影响。车速对车辆行车平稳性影响规律与文献[9]中计算值得出规律基本一致,这也间接证明了本文分析方法及数值模型的正确性。

对比各工况下车辆行车平稳性随信号采集频率变化趋势可知,对于车辆垂向行车平稳性指标,当信号采集频率从20 Hz升高到40 Hz时,幅值精度大幅提高,信号采集频率于40 Hz增大至200 Hz时,信号混叠逐渐减少使得垂向行车平稳性指标减小,信号采集频率达到200 Hz之后,垂向行车平稳性指标趋于稳定;对于车辆横向行车平稳性指标,在信号采集频率从20 Hz升高到200 Hz过程中,车速为60 km/h和90 km/h的幅值精度不断提高,车速为30 km/h时,出现信号混叠,随着采样频率的增大,混叠程度逐渐减小,同样,信号采集频率达到200 Hz以上后,横向行车平稳性指标趋于稳定。

2.2 信号采集频率对轨道梁响应的影响

轨道梁振动信号采集点位于跨中底部,加速度传感器信号采集频率范围为200～3 000 Hz,在自车辆开始上桥到车辆完全出桥这一时间段内进行振动加速度信号采集,得到的轨道梁跨中振动时程曲线,图7即车速60 km/h时,信号采集频率为200 Hz和2 000 Hz下的轨道梁振动加速度时程曲线对比图。观察对比图可知,信号采集频率提高为2 000 Hz时,更多高频信号被采集到,有效减少了实际的高频信号被低频采样而混叠输出为低频信号。

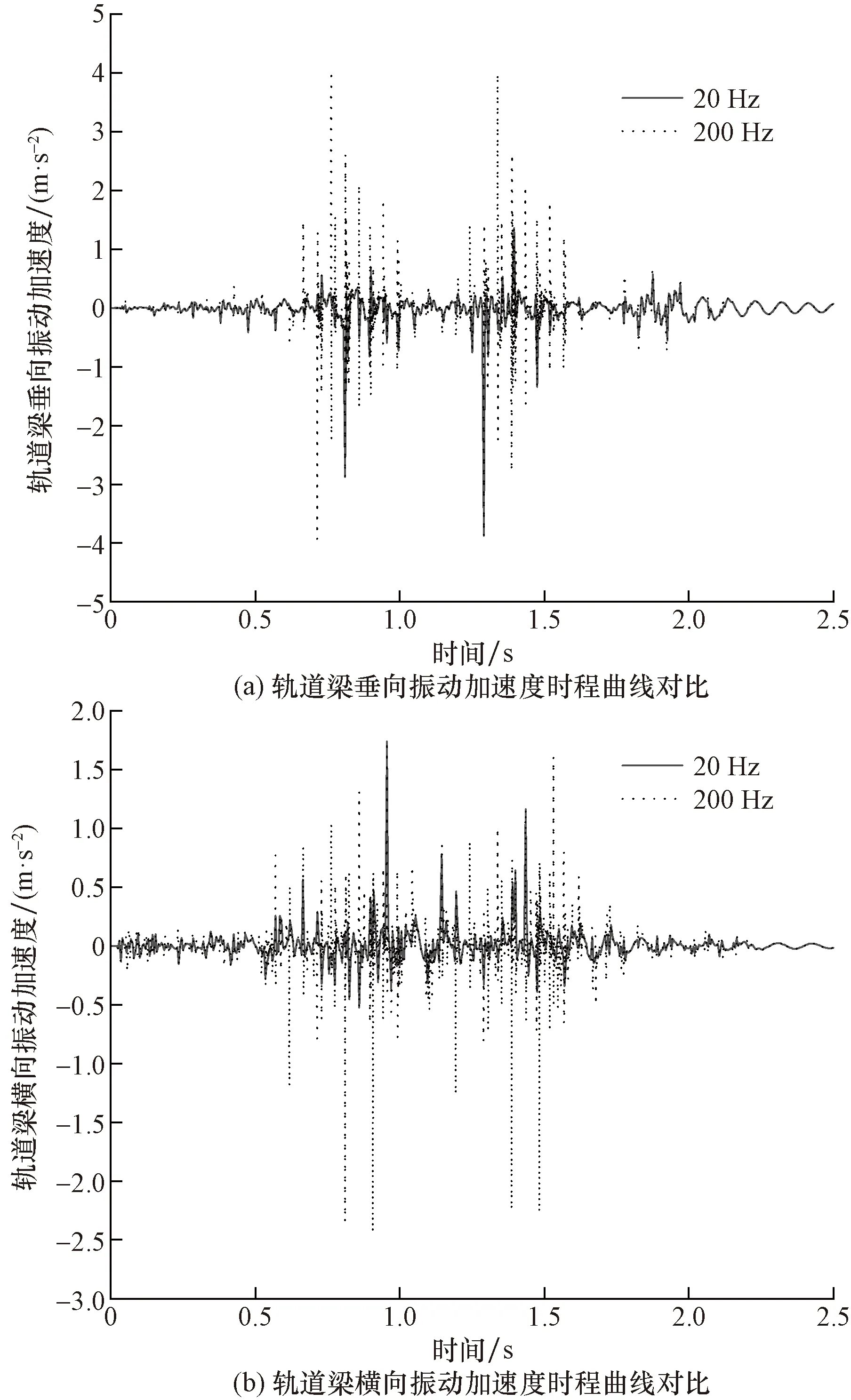
图7 200 Hz和2 000 Hz采样频率下的轨道梁振动加速度时程曲线对比Fig.7 Comparison of vibration acceleration time history curve of track beam at 200 Hz and 2 000 Hz sampling frequency

将信号采集得到的轨道梁振动加速度时程曲线通过40 Hz低通滤波处理得到如图8所示的不同车速下轨道梁振动加速度随信号采集频率变化的趋势。

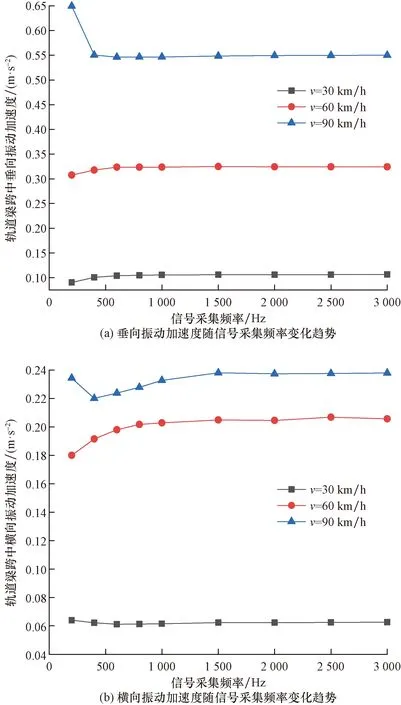
图8 不同车速下轨道梁振动加速度随信号采集频率变化趋势Fig.8 The dynamic acceleration of rail beam varies with signal acquisition frequency at different speed

对比各工况下轨道梁振动加速度随信号采集频率变化趋势可知,对于轨道梁垂向振动加速度,当信号采集频率从200 Hz升高到600 Hz时,信号混叠得到有效控制,幅值精度大幅提升,当信号采集频率达到600 Hz以上后,轨道梁垂向振动加速度趋于稳定;对于轨道梁横向振动加速度,当信号采集频率从200 Hz升高到1 500 Hz时,信号混叠程度减弱,满足幅值精度要求,当信号采集频率达到1 500 Hz以上后,轨道梁横向振动加速度趋于稳定。车速为30 km/h时,轨道梁振动响应较弱,随着信号采集频率的增大,轨道梁振动加速度变化较小。