控制系统性能评估技术发展综述

王志国,储天舒,田 静,刘 飞

(江南大学轻工过程先进控制教育部重点实验室,江苏 无锡 214122)

0 引言

控制性能评估(control performance assessment,CPA)是以工业应用为导向的研究领域。工业对生产性能和产品质量不断增长的需求,推动了CPA技术的发展。Bauer[1]近年来的调查表明,CPA技术已被广泛应用并发展出了一系列相关软件工具。然而,控制回路中的故障和低水平的生产仍然广泛存在。一项来自不同行业的调查表明[2]:85%的控制器在自动模式下运行低效;65%的控制器整定不佳;30%的控制回路在手动模式下运行。从控制回路的角度看,造成性能恶化的主要原因包括控制器不佳、阀门非线性、过程时延、受控过程设计不当、传感器故障和外部干扰。CPA的主要目标是通过1个在线的自动化程序,评价当前控制系统的性能,从而帮助工作人员判断其是否达到要求。

与CPA接近的概念是控制性能监控(control performance monitoring,CPM)。一般两者不加以区分。Huang[3]认为CPM应该融合CPA和过程监控这2种技术。从现有大量文献来看,“评估”更多涉及性能基准的计算,从而实现对当前控制回路整体性能的量化;“监控”通常依靠数据驱动,利用统计分析的手段检测和诊断回路的部分环节。

20多年来,CPA不断取得新的进展。1998年,Qin[4]针对基于模型的性能评估技术,重点综述了最小方差(minimum variance,MV)性能基准及其在比例积分微分(proportional integral differetial,PID)控制器中的适用性。Jelali[5]从不同性能基准的角度回顾了CPA技术的发展,列举了已经开发或上市的工业CPA软件工具。薛美盛等[6]梳理了CPA的完整步骤,指出非线性和时变系统的评估以及与部件性能监测的结合需引起关注。Ding和Li[7]概述了部分现有CPA技术的局限性,提出了1个预测性的统一性能评估框架,展望了3种未来有潜力的发展方向。在CPM的一些细分领域:Gao[8]从大数据背景出发,探讨了控制器自动维护的可行方案;Dambros[9]总结了CPM中使用的振荡监测技术;还有一些研究工作专注于阀门粘滞诊断技术[10-11]。

本文以各种可能引起工业控制系统性能下降的原因为切入点,侧重阐述数据驱动的CPA技术,以便学术和工业界在评估、检测和诊断方面的工作开展;同时,介绍了若干公开数据库,指出了现有技术的不足,提出了发展展望。

1 控制性能下降原因

调查显示,工业控制系统中有41%的控制回路性能可归类为“一般”或“差”。即使刚使用时表现良好的控制回路,其性能通常在一段时间后会出现下降[12-13]。虽然性能下降原因多样,但大多数原因集中在回路的几个组成部分。本小节简要说明性能不佳的常见原因。控制回路中的CPA如图1所示。

图1 控制回路中的CPA框图

1.1 控制器缺乏维护

自动控制系统中,尽管可能有其他更合适的控制器结构,但90%以上的回路还是使用PID控制器。在设备投产之初,控制器能够被仔细地调试和整定。但随着时间的推移,控制器往往数年得不到维护。在这期间,控制器性能下降的可能原因包括以下4点。

①控制器初始设计和整定问题。出于成本和时间考虑,控制器的设计没有考虑系统中被控变量之间的相互作用,尤其在流程工业中没有考虑补偿经常出现的大滞后、强耦合问题。受限于工程师的经验能力,在投产之前可能并没有对控制器参数进行良好的整定。

②对象特性变化。随着时间推移,被控对象的磨损增加、执行机构的摩擦加剧、工厂改造导致控制策略更新、生产原料变化导致回路设定值变化。这些因素使得原控制器参数设定不再适用。

③未及时整定控制器。1个工厂可能有成百上千个控制回路。面对庞大的系统,企业的维护工程师人数不足,没有时间对所有控制器进行严格的测试和优化,一般只是解决“不稳定”甚至“不可用”的控制器。大多数控制器自安装开始只被整定过1次。

④未升级自动化系统。流程工业中许多工厂的控制系统已经有很多年的历史。面对越来越多的数据处理和性能评估需求,系统的计算能力可能无法达到要求。

1.2 阀门非线性

流程工业的控制回路中普遍存在振荡问题,这会导致性能下降。通常认为,阀门非线性是振荡的主要原因,而阀门粘滞是非线性的主要来源。非线性还包括阀门间隙、饱和、迟滞、阀门尺寸失配和非线性流量特性等次要来源[14-15]。图2描绘了几种阀门非线性特性。

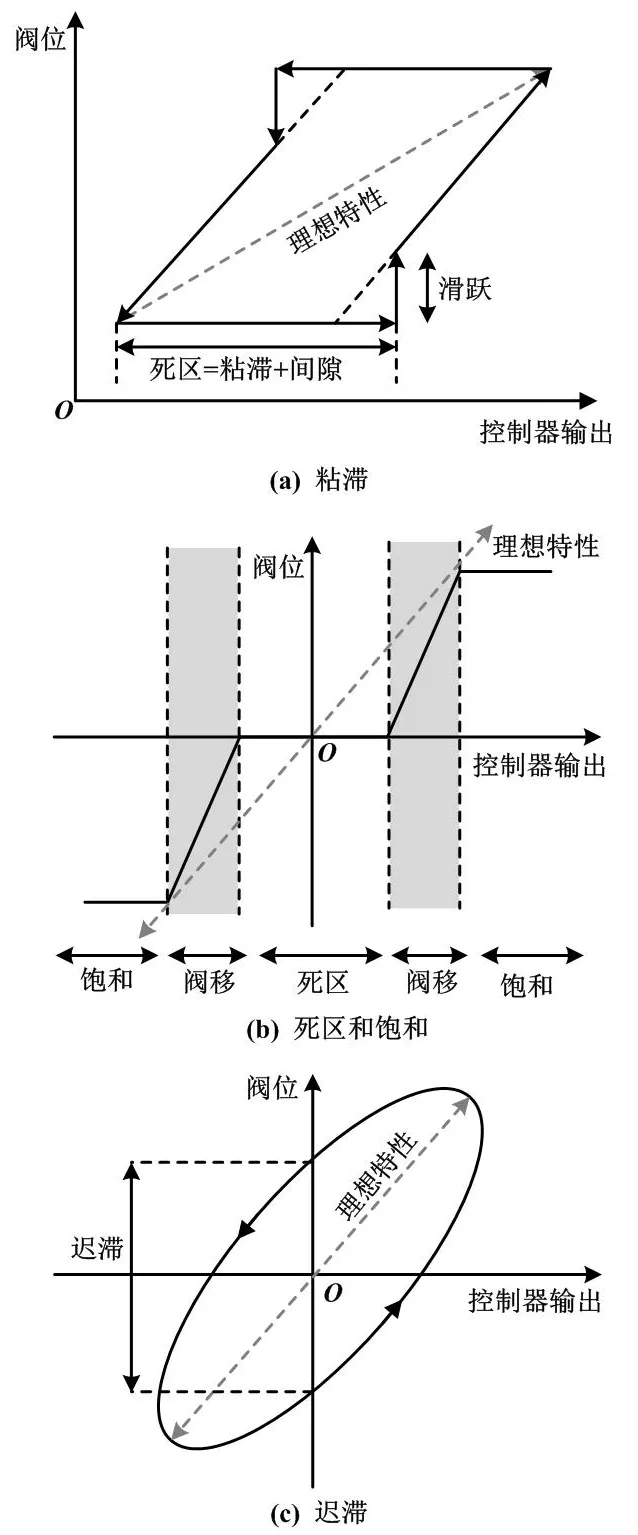
图2 阀门非线性特性示意图

①阀门粘滞。阀门粘滞特性表现如图2(a)所示。当阀杆反向动作时,静摩擦力大于滑动摩擦力,导致需要增大控制器输出才能驱动阀杆运动。阀杆被卡住不动的阶段称为粘滞。当阀门定位器使用更大的压力迫使阀杆运动时会产生滑跃。这容易使阀杆再次卡住,导致粘滞和滑跃交替出现。此时,控制器输出信号会出现锯齿或三角形振荡。一般认为,当移动阀杆所需的额外控制器输出信号超过其正常信号范围的5%时,就会激发振荡现象[16]。

②阀门间隙。当阀门的机械零件中存在间隙时,会增加移动阀杆所需的时间。对于闭环回路,间隙也可能导致振荡。与粘滞不同的是,其引起的振荡信号峰值呈圆形,更像正弦波[17]。粘滞和间隙共同组成了阀门死区。

③饱和。如图2(b)所示,当阀门已经处于全开或全关状态时,控制信号的继续增加或减少不会产生实际动作。

④迟滞。如图2(c)所示,迟滞指当阀杆反向时,相同输入信号会导致不同的阀门位置。在闭环系统回路中,其产生的非线性并不显著。

⑤阀门尺寸与流量特性。一方面,过大或过小的阀门会对控制信号产生不合适动作,使上述问题进一步恶化。另一方面,阀门尺寸不当可能放大流量的非线性特性,导致流量过大或不足,从而引起回路振荡。

1.3 过程对象问题

本文将被控对象和传感器纳入过程对象的范畴。这其实是整个控制回路中最为复杂的部分。虽然调整控制器是提升回路性能的主要方法,但大多数控制性能问题本质上都来自于过程对象。以下总结了一些常见问题。

①工艺设计不佳或设备故障。过程对象的工艺设计决定了控制器性能所能达到的上限。有时,1个性能一般的控制器在易于控制的过程中表现良好,而先进的控制器可能也无法弥补工艺流程的缺陷。一般而言,设备故障可以更换或维修,而工艺问题往往难以重新改造,并且通过调整控制器进行改善的空间不大。

②复杂的对象特性。由于工艺的固有特性,被控对象可能为多变量、强非线性、大滞后。被控变量之间存在相互作用,给控制带来较大难度。

③外部振荡干扰。在实际工厂环境中,干扰可能来自多个方面,如环境温度的升降、风力的波动、原料和产品数量的变化。如果没有采用前馈控制对其进行补偿,这些外部干扰可能导致输出振荡。

④传感器故障。传感器的精度可能会随时间推移而下降。根据优化控制和实施性能评估的需要,应考虑及时更换和添加新的传感器。

2 CPA方法

控制系统的性能一般指其处理受控变量与设定值偏差的能力。通常用1个性能指标来量化这种能力。当控制回路出现确定性干扰或设定值变化时,往往采用传统的性能指标,如上升时间、调节时间、超调量、稳态偏差或者误差积分来评价其性能。CPA技术更关注使用方差衡量控制器的随机性能。被控变量的方差能够反映产品质量和稳定性,与企业效益直接相关。

通常使用理想性能与实际性能的比值来计算性能指数。由于理想性能难以实现,比值通常在0～1之间。比值越接近1,则意味着性能越好。CPA技术发展至今,涌现了许多估计理想性能的方法,并以此为基准来评估控制性能。由于实际工业中控制器和被控对象类型多样,研究人员针对多种实际情况开发了不同的评估方法。此外,数学工具和数据驱动技术的发展丰富了性能评估方法。

2.1 性能评估指标

2.1.1 MV指标

CPA的研究可追溯至1967年,建立在随机控制理论的基础上。Astrom[18]把最小方差控制(minimum variance control,MVC)应用在造纸机控制中。随后,Devries 和Wu[19]通过对比实际输出方差与理论MV,评价过程控制的有效性。Harris[20]则提出了标志性的以MV为基准的性能指标η。

(1)

式中:d为过程时延;fi为噪声信号激励的闭环脉冲响应系数。

Desborough和Harris[21]指出,无需求解Diophantine方程,通过输出数据的自回归分析和过程时延的先验知识,可以很轻松地估计出MV性能指标。

研究学者从多个方面对MV性能指标进行推广和完善。对于不同的控制结构,Desborough和Harris[22]认为单个反馈控制器的性能有限,并将MV性能指标应用在前馈加反馈的控制回路评估中。这种方法具有非侵入性,估计最优性能时只需使用常规运行数据,无需对回路进行额外测试。Stanfelj等[23]使用MV分析方法诊断前馈控制器的性能。McNabb和Qin[24]提出子空间投影法估计前馈-反馈控制系统的MV性能。Ko和Edgar[25]提出了串级控制回路的MV性能评估方法。Thornhill[26]等研究了设定值跟踪的CPA问题,分析了设定值变化时控制性能区别于设定值恒定时的原因。McNabb和Qin[24]通过将输出数据投影到设定值变化矩阵的正交空间上,消除设定值变化对MV性能计算的影响。Moridi等[27]将MV性能指标应用于切换控制系统的设计中。

对于不同的受控对象。Tyler和Morari[28]将MV性能指标推广到不稳定和非最小相位系统,分析了其对不稳定极点和不可逆零点的敏感性;随后,使用广义似然比[29]检验实际的闭环传递函数脉冲响应系数是否超出范围,以此判断性能恶化程度。Li和Evans[30]研究了线性时变控制系统的MV控制器。Huang[31]针对扰动突变引起的时变过程,提出了以MV为基准的线性时变过程的CPA方法[32]。Olaleye等[33-34]的研究工作也是沿着这一方向开展的。张巍等[35]分别提出了多模型混合时变MV控制准则,并将其应用于多时变扰动系统的性能评估。王志国等[36]以MV为基准,研究了不同结构非线性对象的CPA问题。Lynch和Dumont[37]在估计MV指标时,使用Laguerre网络建模,避免了求解Diophantine方程。Yu[38]等研究了采样抖动对MV性能指标的影响。

MV是一个理想的性能指标,只考虑将过程时延作为限制控制器性能的唯一因素。但有诸多客观原因导致它可能无法实现[39],如过程为非最小相位、执行机构饱和、控制动作激进、采样率约束、鲁棒约束等。由于MV实际上给出了输出方差的下限,以此评价控制回路的当前性能仍然具有指导意义[40]。MV已经在许多实际工业控制系统的性能评估中成功应用[41]。

2.1.2 线性二次型高斯和广义最小方差指标

Huang和Shah[42]认为评估控制器的性能应该考虑控制代价,由此提出了线性二次型高斯(linear quadratic Gaussian,LQG)指标JLOG:

(2)

本文对控制作用施加惩罚权重λ。LQG指标将最小化输入和输出方差的二次函数作为理想性能基准。性能评估时,LQG指标可以通过改变权重提供权衡曲线,并将曲线与实际输入方差对比,从而观察输出波动的改进潜力。

相比于MV性能指标,更实际的LQG指标带来更高的复杂度。这主要体现在最优值求解与模型获取问题上。Kadali和Huang[43]提出使用闭环数据的子空间辨识来估计LQG基准。随后,Danesh Pour等[44]又进一步分析了该方法的模型估计一致性问题,并将该方法推广到串级控制系统[45]。Zhao等[46-47]基于LQG基准评估预测控制系统的经济性能。

同样考虑对控制作用的惩罚,广义最小方差(generalised minimum variance,GMV)基准[48]是MV基准的直接推广。

JGMV=E[(Pcet+Fcut)2]

(3)

式中:Pc、Fc为误差信号和控制信号的权重。

事实上,GMV控制律与MV控制律结构相同。与LQG相比,GMV推导过程更简单。其特点是评估性能的方差计算额外考虑了控制作用。Grimble和Uduehi等[49]分析了权重选择问题。Maboodi等[50]使用非线性GMV控制器概念,对一类用自回归二阶Volterra序列建模的非线性系统进行性能评估。王志国等[51]使用辨识方法获得闭环系统模型,提出了1种基于GMV基准的非线性CPA方法。

2.1.3 其他性能指标

用户自定义指标是CPA的主要研究方向之一。前述MVC要将所有的闭环极点补偿为零,而Horch和Isaksson[52]提出可以由用户选择设定1个极点位置,从而使评估更符合实际情况。在工业实践中,维护工程师通常从系统运行的历史数据中拿出表现较好的一部分来评估当前控制性能[53]。此方法使用的基准被称作“历史数据基准”。林晓钟等[54]引用1种综合相似因子来衡量当前实时数据和基准数据的相似性,再进行CPA。苏成利等[55]提出了1种改进的用户自定义指标CPA方法,简化了算法复杂度。Meng等[56]提出基于方差上下界的性能指标,从而为改善控制性能提供指导。Khamseh等[57]融合了多个评估指标,使基于评估结果的决策更具可靠性。Salsbury和Alcala[58]利用指数加权平均方法开发了2个易于计算且可嵌入PID控制器的指标。Schlegel等[59]引入离散傅里叶变换,提出了基于灵敏度函数的性能指标。Alagoz[60]等提出使用参考干扰比指数来评估闭环控制系统的抗干扰性能。

2.2 限定控制结构的性能评估

2.2.1 PID控制器的性能评估

实际工业控制系统中,超过90%的回路使用PID控制器。文献[61]和文献[62]将控制器的结构限定为PID后,再对MV目标函数进行求解,同时得到了以性能为导向的最优PID参数[63]。

(4)

与LQG指标类似,PID控制器的性能评估存在2个限制条件。

①模型获取。PID控制器的目标函数一般需要过程模型或确定性干扰模型。

②迭代优化。PID控制器的最优化迭代求解计算量大,容易陷入局部最优。有学者建议基于内模控制(internal model control,IMC)设置PID控制器参数,从而简化优化问题。

Grimble[66]基于状态空间模型推导了1个简单的优化方法,无需过程模型。Kinoshita等[67]利用虚拟参考迭代整定(fictitious reference iterative tuning,FRIT)技术对PID控制器的GMV指标进行评估。此外,Yu[68]等提出了1种基于内模控制-积分绝对误差(internal model control-integrated absolute error,IMC-IAE)的指标,以评估PID控制器的设定值跟踪性能。为评估针对不稳定过程设计的PID控制器的设定值跟踪和抗干扰能力,Begum 等[69]提出了基于直接合成-积分绝对误差(direct synthesis-integrated absolute error,DS-IAE)的指标。范惠剑等[70]针对PID控制性能因系统工况等因素出现退化的问题,提出了1种在线CPA及参数校正方法。

2.2.2 模型预测控制的性能评估

过去30多年以来, 模型预测控制(model predictive control,MPC)技术已经广泛应用于化工、炼油、冶金和造纸等行业。因此,使用专门的MPC性能评估技术十分重要。Zhang和Henson[71]、Ko和Edgar[72]分别对MPC和带有约束的MPC系统性能评估进行了研究,删去了基准中的加权控制作用部分。其可以类似于MV,在评价指标中仅关注输出误差。但前者在期望输出计算时考虑了对控制作用的约束。Schäfer和Çinar[73]融合了历史数据与现实性能,将MPC性能评估分为检测和诊断两部分。

虽然多数MPC评估基准都比MV性能指标基准更加现实,但实际工业控制系统MPC设计时假设干扰为随机游走模型,如果性能评估时考虑真实的干扰模型,评估指标往往偏低。此时可能无法区分问题来自模型失配还是控制器整定[74]。最近十年,MPC性能评估方法得到很大发展。针对MPC模型质量问题:Sun等[75]使用闭环数据获得模型残差的MV性能指标基准构造模型质量指数;Betellov等[76]在工业中应用了其提出的一些模型评估方法。针对不同类型的MPC性能差距:Duarte-Barros和Park[77]分别使用MV性能指标、统计过程控制、历史数据指标,对3种MPC算法进行了评估;Domanski[78]对比了非线性MPC的性能。刘詟等[79]采用基于线性二次型高斯基准的MPC双层优化结构,对延迟焦化加热炉的多变量MPC控制进行了经济性能评估和分析;周培杰等[80]提出了1种基于优先级策略的模型预测CPA方法,可实现卡边控制,从而最大化经济效益。另外,一些诸如非高斯统计[81]、分形分析[82]的数学工具被应用于广义预测控制的性能评估中,而平方误差积分(integral square error,ISE)指标[83]也被应用于串级动态矩阵控制中。

2.3 多输入多输出系统的性能评估

性能评估技术的实际应用必然要面对多输入多输出(multi-input multi-output,MIMO)控制系统。前文所述的一些性能评估方法可以直接扩展到这类系统上。同时,面对MIMO控制系统的复杂性,也出现了一些新的评估技术。在MIMO控制系统中,单一的时延信息推广为1种能够表征系统时延的关联矩阵。Huang等[84]使用从过程传递函数矩阵中分解出的下三角关联矩阵推导系统的MV。Harris等[85]借助内模结构,利用关联矩阵的谱分解和Diophantine方程的求解,重新计算了LQG控制最优解,证明了多变量系统的MV输出是1个有限阶的滑动平均过程。

上述方法在求解关联矩阵时既要掌握过程模型的全部信息,又要进行复杂的计算,条件相对严苛。为了解决这个问题,Huang等[42]引入酉关联矩阵(unitary interactor matrix,UIM)。其计算仅需过程模型的前几个马尔可夫参数,通过奇异值分解(singular value decomposition,SVD)技术确定关联矩阵的阶。近年来,许多研究者致力于从数据驱动的角度降低对先验知识的依赖或减少评估过程的复杂性。Ko等[86]提出1种不需要计算关联矩阵,只需要过程的前几个马尔可夫参数和1组闭环操作数据的MV性能估计方法。该方法没有减少先验知识,但简化了性能指标的计算,给出了明确的“一次性”解决方案。McNabb 等[87]不使用关联矩阵,而是从状态空间模型中提取多变量时延(multivariate time delay,MTD)矩阵,推导了状态反馈形式下的MV控制,提出了1种利用数据投影的性能评估方法。随后,上述2种方法在子空间方向上实现了扩展。Kadali等[88]一方面在子空间框架下推导了MV性能指标,证明了过程马尔可夫参数矩阵与关联矩阵的内在联系;另一方面还从状态空间模型的角度重新凝练了评估方法,并在实际工业应用中予以验证。Shang等[89]改进了单一的历史数据指标,提出了基于历史预测误差协方差的多指标评估方法。Wang[90]提出了一种不依赖关联矩阵的概率版性能评估框架。

Huang等[91]在MV的基础上融合期望的闭环动态,提出1种用户定义的性能基准。随后,其进一步提出了1种只需要关联矩阵阶数的次优性能基准,并估计了MV的上下界。MIMO控制系统性能评估的研究除了专注于关联矩阵或其等效形式,还通过构造输入/输出(input/output,I/O)时延矩阵降低了对过程模型的需要。Xia等[92]通过提取每对I/O间的时延,构成I/O时延矩阵,以此计算关联矩阵的阶数,并解决了计算次优性能基准时的模型辨识问题。Huang等[93]利用带系数的I/O时延矩阵判断关联矩阵是否为对角阵,以降低性能评估复杂度。Yu和Qin[94]从I/O时延矩阵中提取左/右对角关联矩阵代替UIM,降低了MV的计算负担。Huang等[95]利用I/O时延矩阵信息,直接从干扰模型的马尔可夫参数中计算MV的性能指标。赵宇等[96]基于多变量MV性能指标,提出了1种以广义MV为基准的多变量系统性能评估方法。

3 性能评估数据集

CPA方法需要使用数据进行验证。数据驱动的方法既可用于对过程对象建模或估计控制系统的性能,也可用于对回路故障的检测和诊断。对于数据的需求催生了一些仿真平台,并由此得以建立了一些公开的数据库。本节将介绍其中4个数据库。

Jelali和Huang[97]建立的数据库包含来自不同过程对象和不同工业部门的测量数据。其按照不同回路分类设置数据结构。其中的回路可能存在故障,也可能性能良好。每个回路均包含对象类型、时间、设定值、采样周期、控制器输出和被控变量等必要信息,还有一些回路附加了控制器参数(如比例增益、积分时间)、输出误差等信息。

Bauer[98]引入了适用于单回路和全工厂范围的控制器性能监控数据库。该数据库的优点在于集成了单变量和多变量对象类型的数据。单回路数据包括设定值、控制器输出、被控变量、采样周期以及数据是否归一化。整个工厂范围的数据集包含了各种控制回路的实测值。另外,每个数据集都附上了1个描述性文件。该描述性文件描写了这些数据集测量过程的相关信息。

著名的田纳西-伊斯曼(Tennessee Eastman,TE)仿真平台也可用于CPA算法测试。其生产的数据具有时变、强耦合和非线性特征,经常用于研究阀门粘滞、控制器整定、外部干扰等性能问题。另外,Rieth等[99]生成了1个额外的TE过程数据集。该数据集包含500次模拟运行数据。其中,20次为故障模拟。每次模拟运行均利用25 h生成训练用数据、48 h生成测试用数据。采样周期为3 min,共分别生成500个和960个样本。其中的Simulink仿真文件包含4个模型:①基于开环策略的模型;②基于分布式控制策略的多回路模型;③与模型②相似但允许冷却剂阀门饱和的模型,此时由于不能减小再循环阀的开度,可能会导致失去对反应器液位的控制;④与模型②相似但具有自优化控制策略的模型。后来,Andersen等[100]提供了1个用户图形界面,可以根据需要产生TE过程数据集。

Dambros等[101]分享了1个从私营油气公司获取的单输入单输出控制系统数据库和1个基于Python的可视化分析工具包。数据库由3个文件组成,其中包含了52个控制回路(多数是流量控制)的设定值、控制器输出、操纵变量、输出变量信息。

4 展望

CPA领域经过近30年的发展,其评估的基准从MV延伸发展出各类其他性能指标。但面对现代工业控制系统的大规模、复杂性、非线性和不确定性等特点,CPA/CPM依然是开放性课题,仍有许多问题值得深入研究。

①实际工业系统或多或少存在非线性。线性系统的性能评估方法并不能直接用于非线性系统。一般而言,线性系统的CPA可通过估计单位脉冲响应系数获得。但对于非线性系统,此等价关系并不存在。另外,非线性过程本身的复杂性,导致描述其特性的非线性模型具有时变或不确定性等。作为基于数据的CPA方法所需的系统辨识环节,可能面临模型结构的多重性和数目庞大的待辨识参数。非线性干扰模型的复杂性也会进一步导致在整个非线性系统建模、是否存在MV性能下限的验证方面面临挑战。

②CPA的首要任务是性能评估。在性能不良时需要进一步诊断性能。对于多种可能导致控制性能不良的因素(如控制器结构不合理、参数整定不充分、传感器和执行器故障以及设备运行中原料类型变化等),使用基于数据的方法值得进一步探究。该方法首先研究单一因素下的控制性能诊断方法,然后据此建立多因素的控制性能诊断框架模型。由于控制系统各部件间以及各对应的性能诊断方法之间存在不确定性,基于Bayesian的控制性能诊断是可以考虑的方法。该方法先建立 Bayesian 网络,再使用样本学习或专家估计等方法获得各节点间的条件概率,最后由 Bayesian 推理确定性能不良的根源。

③值得注意的是,在确定的控制策略下,预测整个控制系统的经济性能具有重要意义。在评估和检测不良回路时,一般遵循从监督控制层到基本控制层的顺序。这是因为企业往往更关注与其利润直接相关的监控部分。经济效益是对整个控制系统进行维护和预测性调整的基础。经济性能预测应包括对经济性能检测和经济性能下降预测这2个部分。

④随着对工业生产的经济性能和产品质量要求的不断提高,学者对复杂控制系统的性能退化预测和恢复方法有更高的期望。CPA的一大目的是为性能改善提供指导。有许多学者提出了性能恢复技术和策略。在这方面的主要方法是重新整定控制器。基于数据驱动的强化学习技术可以对控制器进行在线优化。优化算法分为控制策略评估和策略改进2个步骤。基于强化学习来统一控制、评估、检测和诊断将成为未来的重要研究方向之一。

⑤在过去的几年中,数字孪生技术得到很大发展,并应用了统计学习、机器学习和迁移学习等方法来增强其自学能力。在许多工业部门,数字孪生技术已成为实现控制系统预测性维护和产品全生命周期管理的强大工具。未来,数字孪生技术应开发一些与CPA相结合的相关功能模块,如在线学习更新的系统动力学模型,以及针对复杂控制系统设计的性能评估模块、性能下降预测模块、故障检测和诊断模块等。为了实现结合,在云计算时代相应的服务器平台和开发环境可以为其提供服务。

⑥CPA和过程监控技术的结合值得关注。CPA主要实现对控制器性能的评估、诊断和优化。现有成果主要集中在性能评估阶段,后续的诊断和优化依然没有形成比较系统的方法。而过程监控作为一种质量管理技术,目标是实现对各过程阶段的评估和监控,建立并保持过程处于可接受且稳定的水平。从这个角度看,两者之间存在共通之处。因此,利用过程监控领域已有的丰富研究成果,建立结合2种技术的综合性系统监控、诊断以及决策系统架构值得进一步研究。

还需要指出的是,CPA算法在具体环境中的应用也面临着一些亟待解决的问题。作为一种基于数据的方法,CPA离不开数据采集系统的支撑。现有很多企业的分布式控制系统数据库往往数据存档或数据采样频率较低,不能满足CPA对数据质量的要求。而重新建立数据采样系统则成本过高且难以实施。因此,如何基于现有条件完善数据预处理,以提高CPA结果准确率值得研究。同时,下一代控制系统将配备更好的信息获取和传输设施,具备更强的数据计算能力。这将有助于促进CPA技术的进步。

5 结论

CPA作为1种涉及多种学科、技术集成度高且可覆盖不同工业领域的综合技术,其应用对增加企业经济效益、提高生产效率、维护生产流程安全运行以及提高市场竞争力具有重要意义。本文重点对控制系统性能整体量化和分析技术方面取得的理论和实践成果进行了总结,并对未来CPA领域可期的研究方向进行了展望。相信随着生产企业从“制造”向“智造”的转变,以及工业和信息融合大趋势的推进,CPA作为1种新的智能化技术会日益显示其重要性。