基于非线性干扰观测器的模糊自适应滑模控制

马振九,夏春明,2,赵彤彤,章 悦,曹港生,康高峰

(1.华东理工大学机械与动力工程学院,上海 200237; 2.上海工程技术大学机械与汽车工程学院,上海 201620;3.南通大学机械工程学院,江苏 南通 226019)

0 引言

据《中国卒中报告2019》最新数据统计显示,卒中已经超越心血管疾病成为我国致死致残的首要原因,并呈现年轻化的趋势[1]。偏瘫患者需要对患肢进行康复训练。传统的康复训练会耗费医师大量时间和精力[2]。康复外骨骼机器人作为结合了康复医学、智能制造与人工智能等前沿科技的产物,为解决当下存在的问题提供了新的思路,已成为研究热点[3]。

在康复外骨骼机器人的相关研究中,控制是重要的研究内容。控制效果的优劣直接影响着康复训练的效果。穿戴式上肢康复外骨骼机器人各自由度之间高度耦合,具有很强的非线性,并受到建模误差、传感器信号误差、内外界干扰等多种因素的影响。这给精确跟踪期望运动轨迹带来了极大的挑战[4]。针对这些问题,近年来国内外的学者也提出了不同的解决方案。

初期患者肌肉残余力量不足,需要外骨骼提供完全的助力。此时宜采用轨迹跟踪的被动控制方法,由外骨骼带动患侧完成医师规划好路径的康复动作。目前,被动控制策略主要针对比例积分微分(proportional integral differential,PID)控制[5]、滑模控制[6]和模糊控制[7]等方法进行研究。Ahmed等[8]设计了名为SREx的七自由度上肢外骨骼机器人,采用PID控制器为不同受试者提供各种上肢锻炼方法。该方法控制结构简单、参数固定,如果考虑系统非线性不确定性,控制效果会下降。Riani等[9]提出了1种终端滑模控制策略。该策略的跟踪误差可以在有限时间收敛至零,具有极强的鲁棒性;此外,通过Lyapunov证明了其稳定性和收敛性,但抖振问题仍然存在。Li等[10]设计了模糊控制算法,将摩擦项和干扰项合并之后进行逼近,但外骨骼机器人系统复杂,所设计的模糊规则过多会导致计算量过大,不利于实际控制方法的实现。

基于上述研究,本文针对外骨骼机器人存在多种干扰、控制系统抗干扰性能差、传统滑模控制抖振较大以及轨迹追踪精确性低的问题,提出了1种基于干扰观测器的模糊自适应滑模控制方法。本文设计了模糊自适应方法对机器人运动过程中的摩擦项进行估计,并设计了非线性干扰观测器补偿外界慢时变干扰的力矩。在此基础上,本文结合利用双曲正切函数、特殊非线性fal函数设计的新型趋近律,设计了基于非线性干扰观测器的模糊自适应滑模控制器,对上肢康复外骨骼机器人系统实现了期望运动轨迹的准确追踪。仿真试验结果验证了本文方法的有效性。

1 康复机器人结构及其动力学模型

根据人体结构以及上肢运动的特点[11],本文设计了四自由度上肢康复外骨骼机器人。

四自由度上肢康复外骨骼机器人的4个关节对应于肩关节屈曲/伸展(关节3)、 肩关节外展/内收(关节1)、大臂内旋/外旋(关节2)以及肘关节屈曲/伸展(关节4)。考虑到传统上肢康复外骨骼机器人只能针对或左或右固定一侧进行康复训练,本文所设计的外骨骼结构具有对称性,可以通过拆卸和组装转换康复训练的方向,使1台设备适配左右两侧手臂,以满足不同患者的需求。四自由度上肢康复外骨骼机器人结构如图1所示。

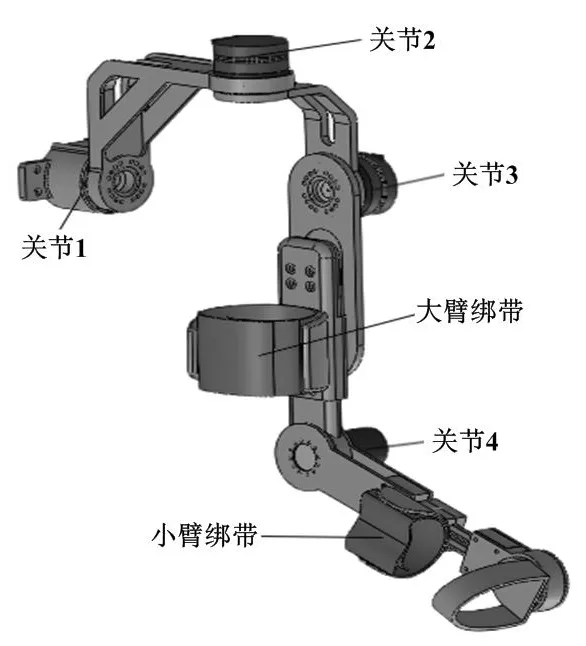
图1 四自由度上肢康复外骨骼机器人结构

在完成运动学计算的基础上,本文采用拉格朗日方法建立动力学模型,对外骨骼机器人进行运动学计算。拉格朗日算子计算式为:

L=K-P

(1)

式中:K为外骨骼机器人系统的总动能;P为系统的总势能。

关于总动能以及总势能的计算可参考文献[12],本文中不再赘述。

本文将拉格朗日算子代入拉格朗日动力学方程,则:

(2)

根据所求力矩可以得到四自由度上肢康复外骨骼机器人的理想动力学模型:

(3)

本文机器人关节均为转动关节,因此τ∈R4。

结合工程实际,由于关节副之间存在多种摩擦力矩,同时外骨骼受到来自外界的慢时变干扰力矩,本文在理想动力学模型中加入摩擦项以及慢时变干扰项。动力学模型如下。

(4)

所建立的外骨骼机器人模型为之后控制的试验仿真奠定了理论基础。机器人动力学模型具有以下性质。

①性质1M(q)矩阵有上下界:

(5)

式中:λmin、λmax分别为M(q)的最小特征值和最大特征值。

(6)

2 新型复合控制器设计

根据第1节计算获得的外骨骼机器人动力学模型,本文提出结合模糊自适应控制、非线性干扰观测器以及滑模控制的新型复合控制方法,设计了基于非线性干扰观测器的模糊自适应滑模控制。该控制方法由干扰补偿项和滑模控制项构成。干扰补偿采用主动抗干扰的策略对系统存在的干扰进行估计并加以抑制。与传统的反馈控制相比,加入干扰补偿的控制方法能够有效抑制扰动。

本节对外骨骼的补偿分为2个部分,分别为模糊自适应补偿和非线性干扰观测器补偿。由于外骨骼机器人受到多种干扰,传统控制方法无法对预期运动轨迹进行准确跟踪,从而无法保证外骨骼控制系统的鲁棒性。因此,考虑到多种不确定因素,本文先通过模糊自适应补偿器对库伦摩擦、粘性摩擦等摩擦部分进行估计,再利用干扰观测器对外部慢时变干扰进行估计,并分别进行力矩补偿。此外,滑模控制是1种非线性控制方法,具有较强的抗参数摄动性,对于外骨骼建模精度要求不高,但存在抖振严重的问题。因此,本文通过设计新型趋近律以及滑模控制器,减小抖振并提高控制器的响应速度。

2.1 针对摩擦项的模糊自适应补偿

Chen[13]提出1种非线性干扰观测器的设计方法。但该方法针对的惯性矩阵必须满足特殊形式,因此有很大的局限性。Mohammadi[14]对该方法进行改进,提出1种可以同时逼近摩擦干扰以及外界慢干扰的方法。本文外骨骼机器人有4个关节,每个关节输入量为3,每个输入变量设计5条隶属度函数,共有512=244 140 625条规则。计算量过大不利于控制器的实际运用。为减少模糊规则总数、提高运算效率,本文分别对摩擦干扰部分和外界干扰部分进行补偿。此外,机器人系统中摩擦干扰不属于慢时变干扰,通过非线性干扰观测器逼近效果不佳[15],因此在设计非线性干扰观测器前必须通过模糊补偿来逼近摩擦项干扰,以减少模糊规则的数量、提高运算效率,并增强系统的抗干扰能力。

模糊系统具有万能逼近特性,通常情况下定义其输出形式如下。

Y=ξT(x)Θ

(7)

式中:x、Y分别为输入与输出;ξ(x)为回归向量;Θ为参数向量。

回归向量表示为ξ(x)=[ξl(x),…,ξm(x)]T。l、m分别为隶属度函数数量以及模糊规则数目。ξl(x)又称基函数。本文中,回归向量表示为:

(8)

常见的隶属度函数有高斯型、梯形以及三角形等。本文选取高斯型隶属度函数。高斯形隶属度函数曲线如图2所示。

图2 高斯型隶属度函数曲线

本文定义qd为期望轨迹关节对应角度,则轨迹跟踪误差为:

e=q-qd

(9)

本文定义滑模函数为:

(10)

式中:Λ=diag(Λ1,Λ2,Λ3,Λ4),且Λ为正定矩阵。

为求解输出值,必须对模糊推理得到的模糊矢量进行解模糊化。本文采用乘积推理机、单质模糊器以及中心平均解模糊器,得到4个关节的摩擦补偿值:

(11)

通过以上模糊自适应补偿器的设计,可以抵消摩擦项对于外骨骼机器人的干扰,从而提高系统的抗干扰性能。

2.2 针对慢时变干扰项的干扰观测器

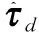
(12)

本文将干扰估计导数值写成以下形式:

(13)

对式(12)求导,得:

(14)

误差方程为:

(15)

(16)

非线性函数向量p为:

(17)

式中:X为可逆矩阵,可通过线性矩阵不等式求解。

(18)

本文对式(17)求导后,结合式(16)、式(18)可得:

(19)

因此,本文设计以下非线性干扰观测器。

(20)

由第1节可知,惯性矩阵M(q)为正定矩阵。为了判定非线性观测器的稳定性,取Lyapunov函数为:

V0=KTXTM(q)XK

(21)

对式(21)求导,得:

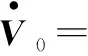
(22)

线性不等式为:

(23)

式中:Γ为正定矩阵,Γ>0。

因此,式(22)可转换为:

(24)

K(t)=K(t0)exp[-L(q)·t]

(25)

由式(25)可知,外骨骼机器人受到外界干扰时,非线性干扰观测器是稳定的,并可有效、快速收敛。

2.3 滑模控制器的设计

传统的滑模控制在一定程度上能够追踪期望轨迹,但其本质上存在的动态非线性会使得控制量存在很强的抖振。这一问题增加了能量的消耗,且对于硬件系统的安全以及控制系统的控制精度都不利。因此,需要设计新的非线性滑模趋近律来改善传统滑模控制在受到干扰的情况下抖振严重的问题。

(26)

非线性函数为:

(27)

式中:0<α<1;δ为影响趋近速度的常数,又称为边界层宽度。

本文提出的新型滑模趋近律为:

(28)

2.4 控制律设计及其稳定性分析

结合计算力矩法、模糊自适应补偿器、非线性干扰观测器以及新型滑模趋近律,本文设计的控制律为:

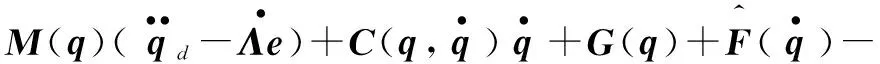
(29)

对滑模函数求导:

(30)

因此,有:

(31)

设计系统Lyapunov函数为:

(32)

(33)

Lyapunov函数导数值小于等于0,为半负定。根据稳定性判据可知,如果输入力矩为有界函数,则控制器是稳定的,系统误差渐进稳定。通过对摩擦补偿以及干扰观测器对外界干扰的实时辨识估计,能够减小滑模控制中切换增益矩阵的值,且设计的新型趋近律可以进一步降低机器人快速运动中产生的抖振问题的影响,从而提高控制系统的稳定性。

3 控制系统仿真试验

3.1 控制仿真参数设定

为验证所设计控制方法的有效性,本文在Matlab/Simulink环境下对存在摩擦项以及外界慢时变干扰的上肢康复外骨骼机器人系统进行仿真。

根据人体上肢结构以及尺寸,上肢康复外骨骼机器人结构参数如表1所示。

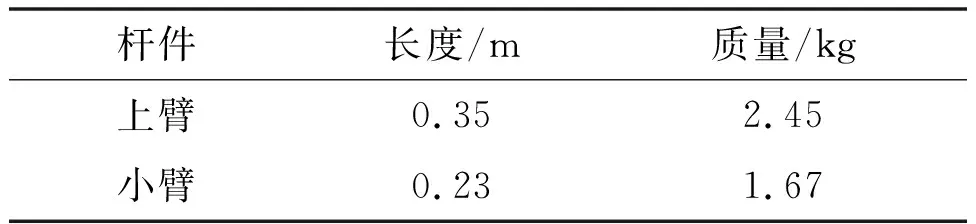
表1 上肢康复外骨骼机器人结构参数

根据前文所述:模糊自适应补偿器中,Λ=diag(10,10,10,10)、ρi=[0.000 1,0.000 5,0.002 3,0.000 4]′;非线性干扰观测器中,可逆矩阵X=diag(0.538 2,0.592 1,0.618 3,0.632 6);滑模控制器中,α=0.25、δ=0.10、W=diag(6,6,6,6)、η=2、β=0.015、K=diag(500,500,500,500)。

4个关节的初始位置参数为q=[q1,q2,q3,q4]′=[0.5,0.2,0.4,-0.2]′。

本文设系统期望运动轨迹为qd1=0.3cos(t)、qd2=0.3sin(t)、qd3=0.3cos(t)、qd4=0.3sin(t)。其中,qd1、qd2、qd3、qd4分别为4个关节的关节角度。

3.2 仿真结果及分析

为验证本文所提控制方法的有效性,本文增添对照组。控制器1通过传统线性滑模控制方法对期望运动轨迹进行跟踪仿真,在控制器中不采用模糊自适应控制器、非线性干扰观测器对系统中的不确定项进行估计。控制器2为在线性滑模控制器中加入模糊自适应补偿器以及非线性干扰观测器。控制器3采用本文所设计的复合控制方法。

①位置追踪分析。

为验证本文控制方法的有效性以及优越性,对比控制器1、控制器2、控制器3这3种控制方法,对其分别进行轨迹追踪仿真。

轨迹追踪位置曲线仿真结果如图 3所示。

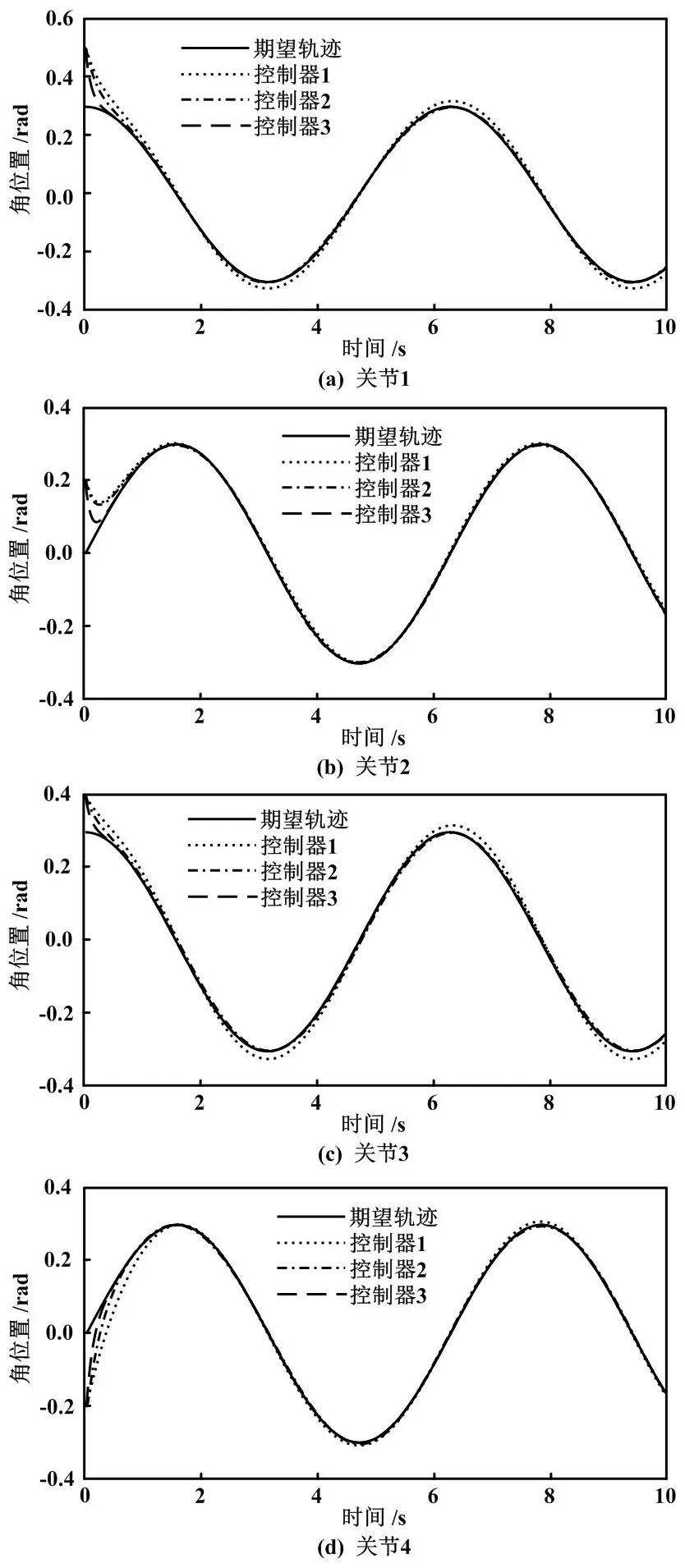
图3 轨迹追踪位置曲线仿真结果

图3中展示的3种控制方法都能够在一定程度上完成轨迹追踪的任务。由图3可知,在控制器中加入模糊自适应补偿以及非线性干扰观测器补偿后,关节能够准确地跟踪期望轨迹,误差非常小,几乎为0;而没有加入补偿的方法在轨迹跟踪中存在一定的跟踪误差以及相位误差。

为进一步比较3种控制器的控制结果,本文绘制轨迹跟踪误差曲线。不同控制方法下的轨迹跟踪误差曲线如图4所示。

图4 不同控制方法下的轨迹跟踪误差曲线

由图 4可知,基于非线性干扰观测器的模糊自适应滑模控制方法可以有效地提高控制系统的鲁棒性。当外界存在多种摩擦以及慢时变干扰,相比于其他2种传统控制方法,本文提出的控制方法可以使外骨骼机器人以较快速度从初始位置趋近期望轨迹,从而提高响应速度。采用新型复合控制方法减小了干扰对于轨迹跟踪的影响,大幅提高了轨迹追踪的精度,并改善了传统滑模控制抖振严重的现象。这能够满足上肢康复外骨骼机器人的高精度轨迹追踪的控制要求。

②摩擦项的模糊自适应补偿分析。

本文采用模糊自适应补偿的方法,对系统受到的摩擦进行估计,并将估计值反馈给控制系统,以降低系统受到摩擦的干扰。4个关节的摩擦项补偿曲线如图5所示。

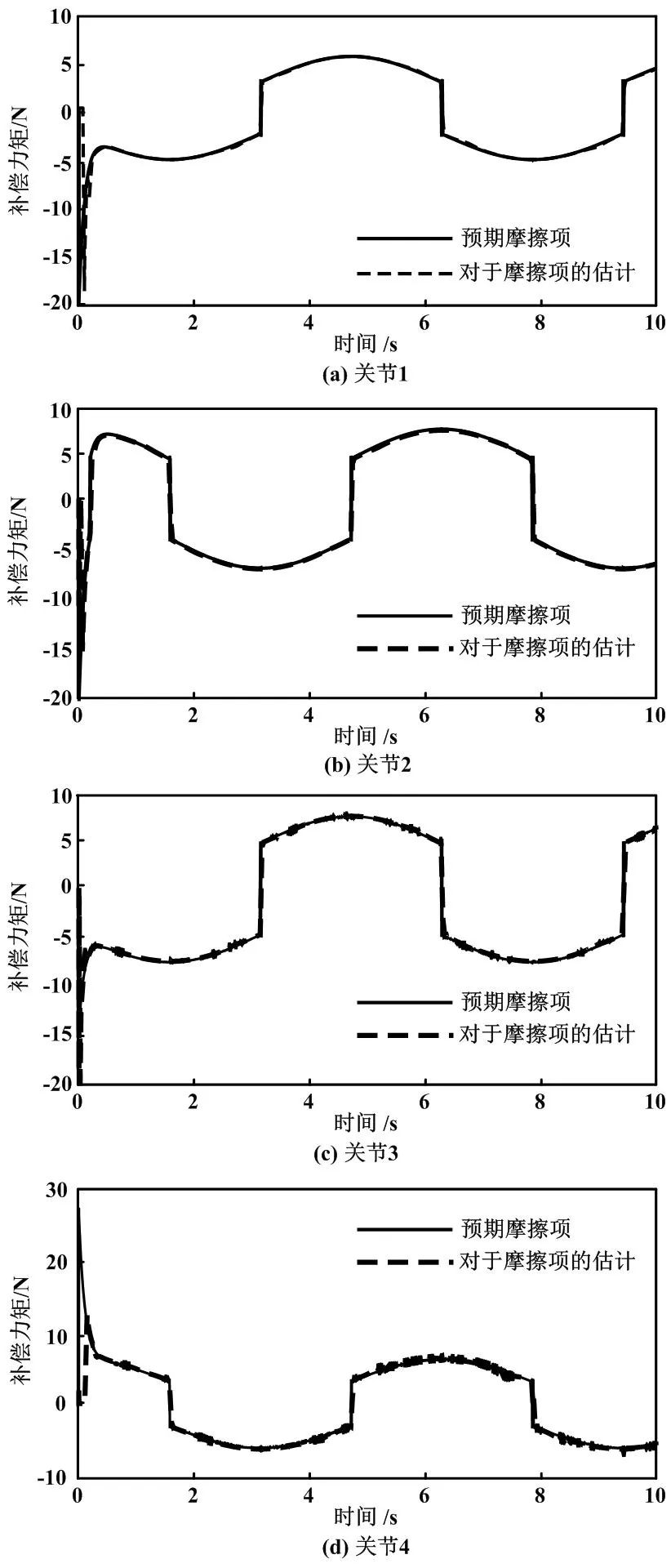
图5 4个关节的摩擦项补偿曲线

由图5可知,模糊自适应项逼近摩擦项设定值的速度较快,且逼近精度较高,极大程度地提高了控制系统的鲁棒性。

③非线性干扰观测器分析。

本文所设计的非线性干扰观测器可以针对上肢康复外骨骼机器人慢时变扰动进行逼近。4个关节的非线性干扰观测器补偿曲线如图 6所示。

图6 4个关节的非线性干扰观测器补偿曲线

由图6可知,所设计的观测器可以有效地对干扰进行实时估计,并以较高的精度逼近系统干扰量。在机器人受到外界力矩干扰的情况下,控制系统将观测器估计量作为补偿值,反馈给控制器的观测信号有效地克服了快速运动中的抖振问题,提高了系统控制精度,以及系统整体的抗干扰性。

为进一步比较3种控制策略的结果,本文将控制结果数据化,统计上述3种方法能够稳定跟踪曲线的时间(ts)以及稳定之后的最大跟踪误差。不同控制策略数据统计结果如表2所示。

表 2 不同控制策略数据统计结果

综上所述,采用传统滑模控制方法,且在控制器中不加入模糊自适应控制器以及非线性干扰观测器时,收敛时间较长且跟踪误差较大;加入力矩补偿的2个部分之后,跟踪误差明显下降,收敛时间也有所缩短;采用基于非线性干扰观测器的模糊自适应滑模控制后,精度提高了1个数量级甚至更高,同时进一步缩短了收敛时间,从而大大提高了整个康复外骨骼机器人控制系统的鲁棒性。

4 结论

针对外骨骼机器人系统的不确定性,本文提出了1种新型的复合控制方法。本文主要结论如下。首先,本文在理论的动力学建模中考虑到摩擦以及外界干扰项,设计了模糊自适应补偿器以及非线性干扰观测器对以上2种外界干扰进行补偿,减小了模糊规则的数量,并提高了控制系统的追踪精度。然后,本文结合非线性fal函数设计了新型趋近律,能够保证系统的快速收敛,并改善了抖振现象,进一步提高了系统的控制精度和抗干扰性。最后,本文使用Lyapunov稳定性理论分析本文设计的控制方法的可行性,并进行控制试验仿真。试验结果证明,本文控制方法在控制精度、收敛速度方面都有显著的优势,具有较强的鲁棒性。

综上可知,本文控制方法应用到康复外骨骼上能够提供更精准的康复训练,从而加快患者的康复进程,具有一定的实际应用价值。