运载火箭并联双机姿控配平策略研究

余光学，李 东，娄路亮

(1. 北京宇航系统工程研究所，北京 100076；2. 中国运载火箭技术研究院，北京 100076)

0 引言

运载火箭系统组成复杂、产品数量众多、工作环境恶劣，具有典型复杂巨系统的特征[1-2]。近年来，国内外发生了多起因动力故障引起的飞行异常事故。在出现故障时，火箭依靠标准任务剖面设计余量去“硬扛”，或者是采用自主故障诊断及相应的控制重构措施，能够适应一定的非致命故障情形。一般情况下，当运载火箭具有多台发动机和多个伺服机构工作时，在飞行出现故障时不会瞬时失稳，而是有时变过程的，这为遏制故障的发展并采取一定的应对措施提供了可能性。在非致命故障时火箭仍能够利用剩余能力去完成飞行任务，诸如Falcon 9火箭在一级单发动机出现故障情况下，通过箭上控制重构最终保证任务成功[3]。

在航天运载事故中，推进系统故障导致的重大失败次数占总失败次数的50%以上[4]。针对发动机故障问题，开展故障重构控制，保证在运载器非致命故障下的姿控稳定至关重要，是实现任务鲁棒或者任务降级的前提。一方面摆发动机的控制能力来自于推力，当推力异常时原有的控制设计将受到直接影响；另一方面姿态控制是控制回路的内回路，因此姿态重构控制是容错控制与任务鲁棒设计的基本保证[5]。推力异常或伺服故障容易给飞行任务带来致命影响，不同的摆发动机控制布局具有不同的适应能力，迫切需要在面向智能控制的动力学建模、故障诊断和控制重构技术等方面加大研究与实践。要实现火箭的智能控制，应从摆发动机布局优化角度为全箭提供良好的控制基础，控制律设计则应通过算法充分发挥火箭的硬件功能配置，并加大智能算法与前沿技术在航天领域的应用，软件算法是智能控制的核心之一[6-10]。

本文开展了典型并联双机布局的姿态控制配平仿真研究，首先给出了典型的并联双机控制布局，介绍了液体运载火箭适应推力异常或伺服故障的全量动力学控制建模设计；针对摆发动机控制典型故障模式，基于运载火箭比例微分(Proportional Differential，PD)姿控方法比对了各布局方案的姿控配平仿真结果；最后讨论了一种控制重分配的优化策略和控制效果，推荐了并联双机控制布局优选方案。

1 典型并联双机控制布局

对于两发动机配置，其安装位置可在象限线上，还可在象限线的45°位置；伺服机构可采取十字摆发动机控制方式，也可采取×字摆发动机控制方式。据此交叉组合后可分为4种推力矢量摆发动机控制布局方案，典型的并联双机摆发动机控制布局如图1所示，在此给出了相应的摆发动机控制通道合成摆角与控制分配关系，其中箭头指示为相应伺服机构摆发动机的正方向，各布局图均为火箭尾视图。

(a)布局1(发动机形布局，伺服×字摆动)

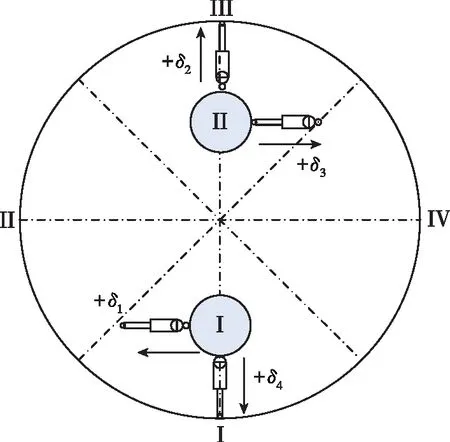
(b)布局2(发动机I形布局，伺服十字摆动)

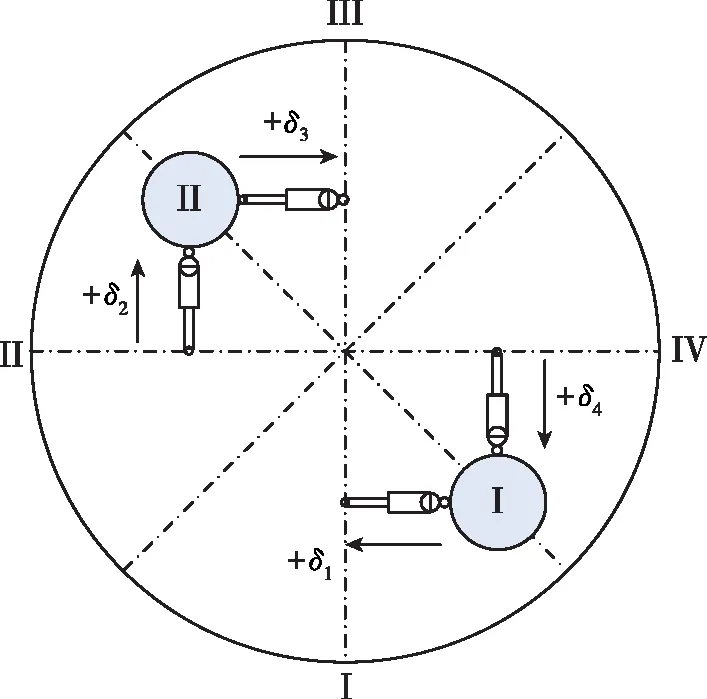
(c)布局3(发动机形布局，伺服十字摆动)

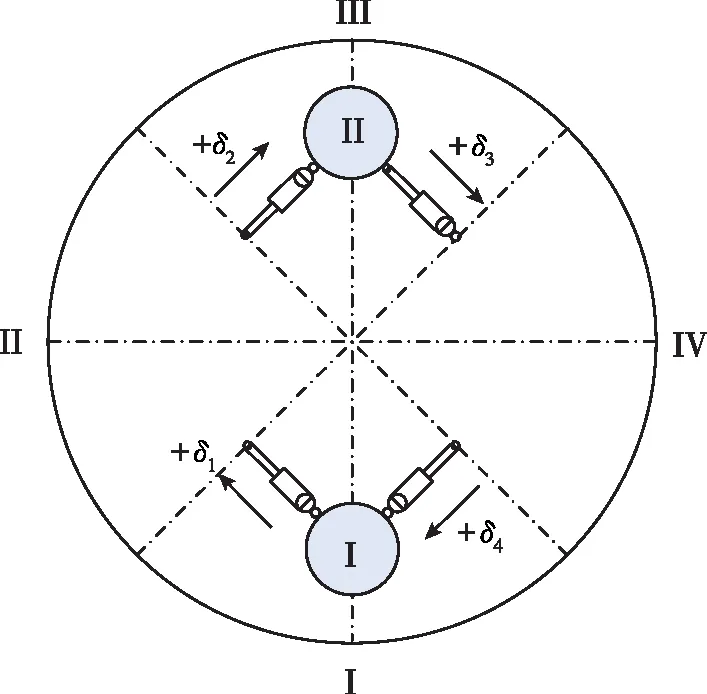
(d)布局4(发动机I形布局，伺服×字摆动)图1 并联双机推力矢量控制布局Fig.1 PCDE thrust vector control layouts

并联双机摆发动机控制布局中，每台发动机安装有2台伺服机构，布局1和2分为沿箭体切向推动发动机和沿箭体径向推动发动机，布局3和4则规避了沿箭体径向推动发动机。4种布局的区别在于：在各伺服机构摆动相同的角度情形下，姿控布局1和4可提供的俯仰/偏航通道控制能力是布局2和3的1.414倍，姿控布局3和4可提供的滚动通道的控制能力是布局1和2的1.414倍。正常飞行条件下，从配平和姿控稳定的角度，姿控布局1和2一致，姿控布局3和4一致。设俯仰、偏航和滚动3个通道的摆角分别为δφ，δψ，δγ，各伺服分机的摆角分别为δ1，δ2，δ3，δ4，那么各布局的发动机通道合成摆角和伺服分机的控制分配关系如下。

布局1的发动机合成摆角与控制分配为

(1)

(2)

布局2的发动机合成摆角与控制分配为

(3)

(4)

布局3的发动机合成摆角与控制分配为

(5)

(6)

布局4的发动机合成摆角与控制分配为

(7)

(8)

以布局1为例开展分析，在发动机II分机推力下降故障模式下，运载器将在俯仰通道产生抬头干扰力矩，偏航通道产生左偏航的干扰力矩，当故障发生后，摆发动机控制伺服摆角合成与分解最佳控制方式将不再满足式(1)与式(2)，需要在克服干扰力矩的条件下结合控制布局进行重分配，这给传统的不考虑故障动力学控制设计带来了困难与挑战。

2 运载器故障动力学建模

为了开展发动机推力下降或伺服故障下的姿控技术研究，必须建立考虑发动机推力与伺服相关联的运载火箭六自由度全量动力学模型，该模型应满足如下要求：

1)能够反映推力异常对质心运动和绕质心运动的影响；

2)能够反映各台发动机故障的特征，模型中应当分别对各台发动机推力影响加以描述；

3)仿真过程中需要考虑发动机故障对火箭质量特性(质量、转动惯量、质心)的影响；

4)推力下降时除了会减小轴向推力和控制力矩以外，还会产生推力不对称的干扰力矩，需要在姿态动力学模型中补充相关干扰项。

以布局1为例，在此针对运载火箭两台发动机×字布局双向摆动动力学故障建模如下：式(9)为质心运动学方程，式(10)为质心动力学方程，式(11)为姿态运动学方程，式(12)为姿态动力学方程。

(9)

(10)

(11)

(12)

相关具体参数的含义参见文献[11-12]。

运载器发动机通常采取面对称或轴对称布局，由于对称性，发动机轴向推力产生的干扰力矩相互抵消，其姿控能力来自摆发动机控制产生的推力矢量。然而当出现某一台发动机推力故障时，轴向力平衡被打破，此时将对运载器产生不平衡的干扰力矩。传统运载器动力学方程与控制设计没有考虑故障的情形，以上动力学方程中抛弃了以往采用合成摆角的控制方式，将各发动机摆角与推力进行了物理关联，从而反映出某一伺服机构或发动机推力故障下对质心与绕心运动产生的力与力矩影响。

新一代液体运载火箭控制器设计，以PD+校正网络设计为主[13]，液体运载火箭姿控方案理论框图见图2，本文采用此控制律开展姿控配平研究。

3 不同故障配平仿真研究

3.1 零推力故障配平策略

在此，针对4种典型布局设定各发动机推力相等，伺服机构最大摆角相同，在运载火箭飞出大气层后开展典型的故障配平仿真研究，结论同样适用于大气飞行段。考虑从200 s开始发动机II推力下降为零的故障模式，在布局1中，此时在发动机I推力作用下将对火箭形成抬头干扰力矩和左偏航干扰力矩，那么在俯仰和偏航通道上均需要伺服δ1和伺服δ4进行配平，滚动通道上为欠驱动。当滚动通道上的系统干扰较小时，滚动姿态角将出现缓慢发散趋势，图3给出了故障情形下的姿态角偏差与各通道合成摆角控制过程，图中Dfai、Dpsi、Dgma分别表示俯仰姿态角偏差、偏航姿态角偏差、滚动姿态角偏差，FY、PH、GD分别表示俯仰通道合成摆角、偏航通道合成摆角、滚动通道合成摆角。由于没有采取控制重分配，PD控制的效果是诱导姿态角偏差，在可用摆角范围内姿态根据初始扰动进行漂移，无法稳定飞行。

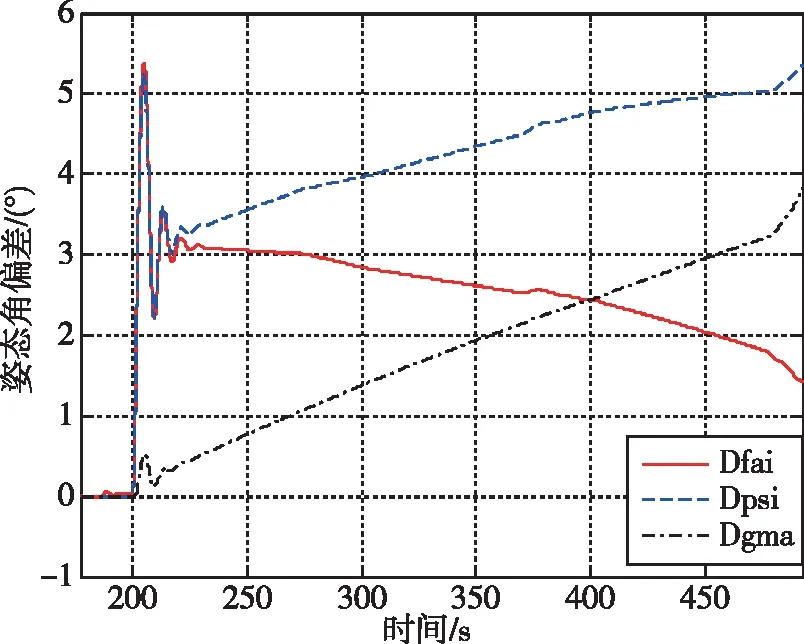
(a)姿态角偏差

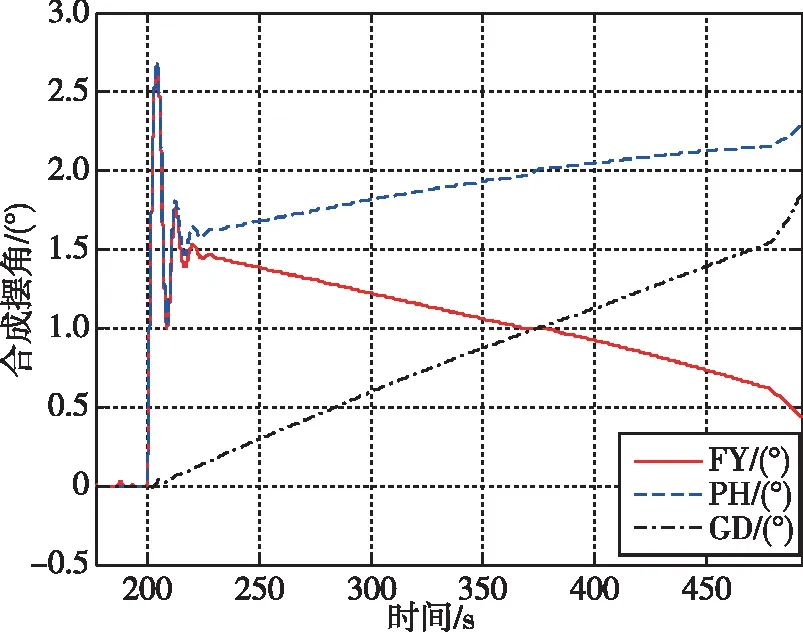
(b)通道合成摆角图3 布局1发动机II零推力故障下的控制配平结果Fig.3 Trim results of thrust II failure for Layout-1

同样地，在布局2中以发动机II推力下降为零的故障模式，此时在发动机I推力作用下将对火箭形成抬头干扰力矩，那么在俯仰通道上需要伺服δ4进行配平，滚动和偏航通道上只有伺服δ1参与控制，也为欠驱动控制问题。此时，伺服机构δ2和δ3无控制能力，处于冷摆状态。在PD控制律和原摆角分配下，伺服机构δ4参与俯仰通道的配平后诱导产生俯仰角偏差。偏航和滚动通道的姿态角速度无法收敛，因此偏航和滚动姿态角发散的快慢取决于结构干扰和初始的姿态角速率大小，仿真结果如图4所示。

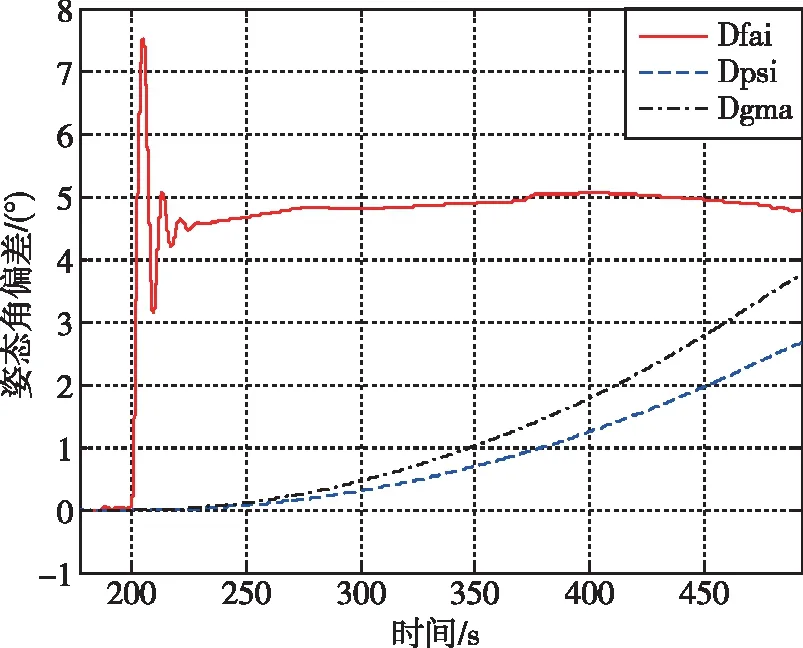
(a)姿态角偏差

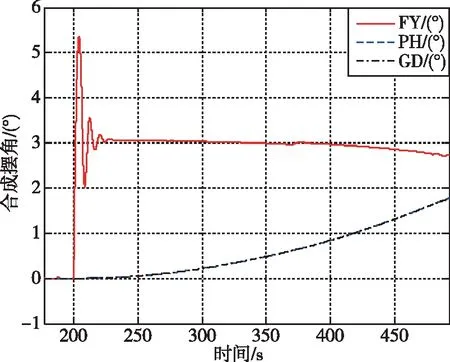
(b)通道合成摆角图4 布局2发动机II零推力故障下的控制配平结果Fig.4 Trim results of thrust II failure for Layout-2

类似地，当布局3和布局4发生一台发动机零推力故障时，姿控配平结果与以上两种情形相似。故障发生后，从姿控稳定的角度，布局1，2，3，4都是两个伺服机构参与3个通道的控制，姿态角速率不能收敛，在初始姿态角速率和干扰作用下，姿态角发生漂移；布局2和布局4的优势在于当发生一台发动机推力故障后其系统干扰为单一俯仰通道，而布局1和布局3则表现为两个通道，故障发生时刻布局2和布局4的偏航和滚动通道的干扰较小，相对来说可以适应更长时间的推力故障情形。

3.2 残余推力配平策略

同样针对布局1，在一台发动机上Ⅱ推力下降到5%，此时滚动通道上控制能力大大减弱，但是并没有完全丧失。图5给出了此故障情形下的姿控配平结果，包括姿态角偏差、合成摆角和伺服摆角的控制响应动态过程，可见发动机残余推力是非常关键的一个控制作用，伺服δ2和δ3仍可有效参与姿态控制，此时PD控制将在俯仰和偏航通道上产生静差，滚动通道收敛，姿态稳定，但由于滚动通道控制能力有限，引起了滚动通道抖动。

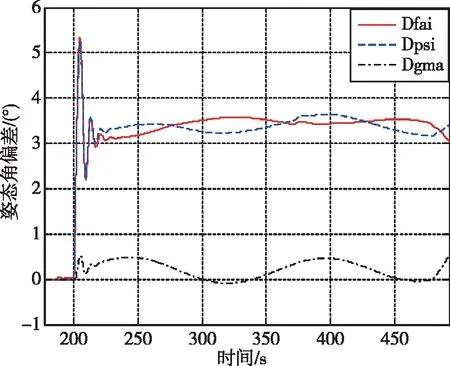
(a)姿态角偏差

(b)通道合成摆角

(c)伺服响应图5 布局1发动机II剩余5%推力故障的配平结果Fig.5 Trim results of thrust II remaining 5% for Layout-1

同时注意到，由于没有采取控制重分配措施，在故障发生时出现了伺服机构饱和的问题，时间持续大约4 s，这对于火箭姿控来说很危险，此段时间内若出现其他干扰，姿控系统无法响应控制作用，第4章将针对此故障案例开展控制重分配策略研究和仿真验证。

同样，在布局4中，发动机为面对称布局，因两台发动机推力大小不一致所产生的偏航和滚动通道干扰较小，偏航和滚动通道的干扰主要由结构干扰和质心横移等因素决定，较为随机。若发动机II分机残余5%推力，伺服δ2和δ3同样可有效参与姿态控制，在结构干扰较小的情形下，此时PD控制将在俯仰产生静差，偏航和滚动通道可控，姿态稳定，仿真结果如图6所示。

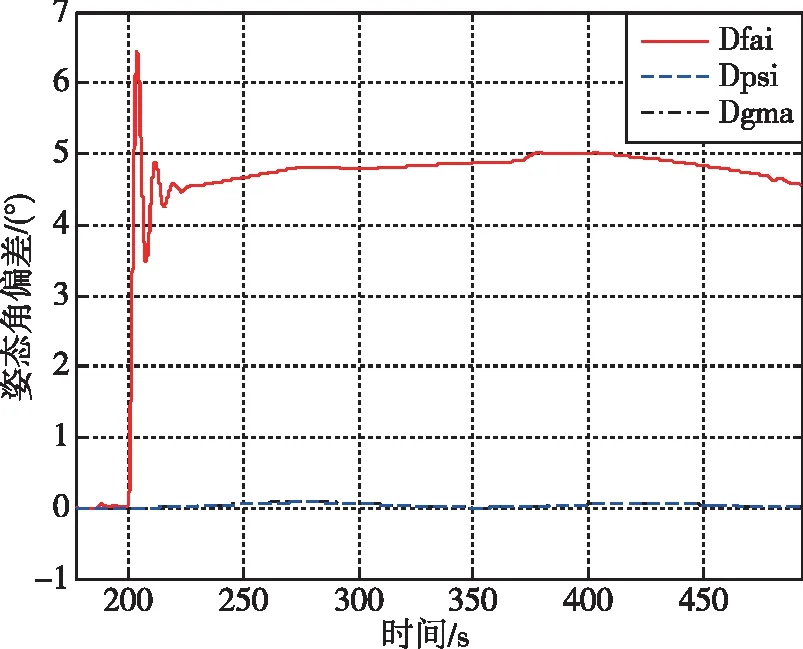
(a)姿态角偏差

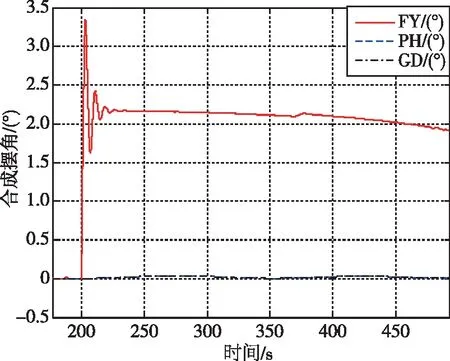
(b)通道合成摆角图6 布局4发动机II剩余5%推力故障的控制配平结果Fig.6 Trim results of thrust II remaining 5% for Layout-4

与此类似，布局2，3的仿真结果与布局1，4相似，如果故障发动机残余一定的推力，那么在结构干扰较小时，姿态是稳定可控的。以上在不采取控制重构方法下，验证了传统PD控制算法条件下的各摆发动机姿控布局对故障的适应性。结果表明，传统的控制律基于负反馈控制具有一定的故障适应能力，若发生推力故障的发动机存在一定的残余推力，只要不存在大的干扰作用，现有的4种布局均可适应此类故障，在可用摆角范围内姿控均是稳定的。

3.3 伺服卡滞故障策略

在此以布局1为例，分别给出了切向伺服机构(取伺服δ1)和径向伺服机构(取伺服δ2)卡滞固定角度情形下的姿态控制结果。图7为伺服机构δ1卡滞0.02°故障情形下姿态角偏差和通道合成摆角动态，此时伺服摆角将很快饱和，使得姿控失稳；图8为伺服机构δ2卡滞2°故障情形下姿态角偏差和伺服响应动态，此时姿控稳定。可见，在布局1中，火箭芯级两台发动机伺服机构按形布局作×字摆动，当两台分机中的切向摆动伺服出现故障时，箭体则无法实现稳定控制，飞行姿态发散，此为这种姿控布局固有的致命故障模式，此类故障导致火箭滚动通道上没有控制能力，比推力下降故障更加危险。

(a)姿态角偏差(发散)

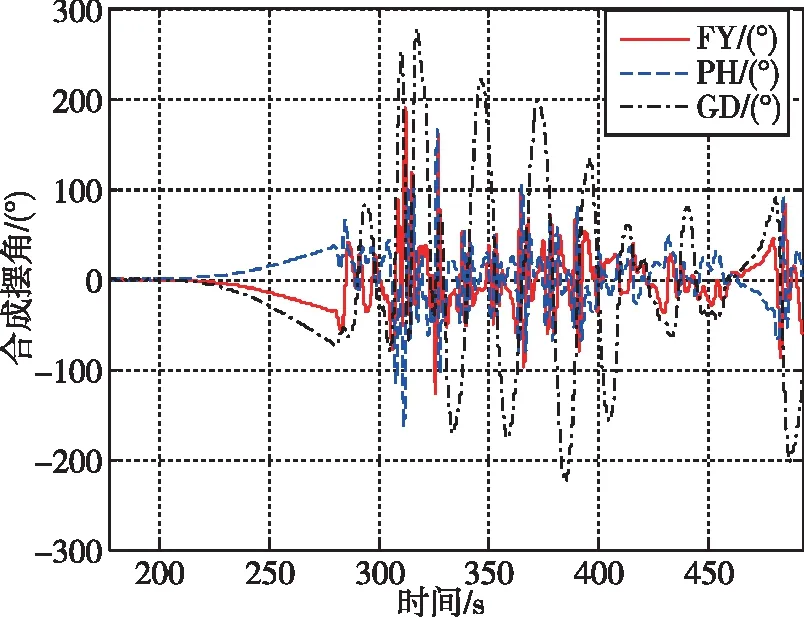
(b)通道合成摆角(饱和)图7 布局1伺服机构δ1卡滞0.02°的控制配平结果Fig.7 Trim results of δ1≡0.02° for Layout-1

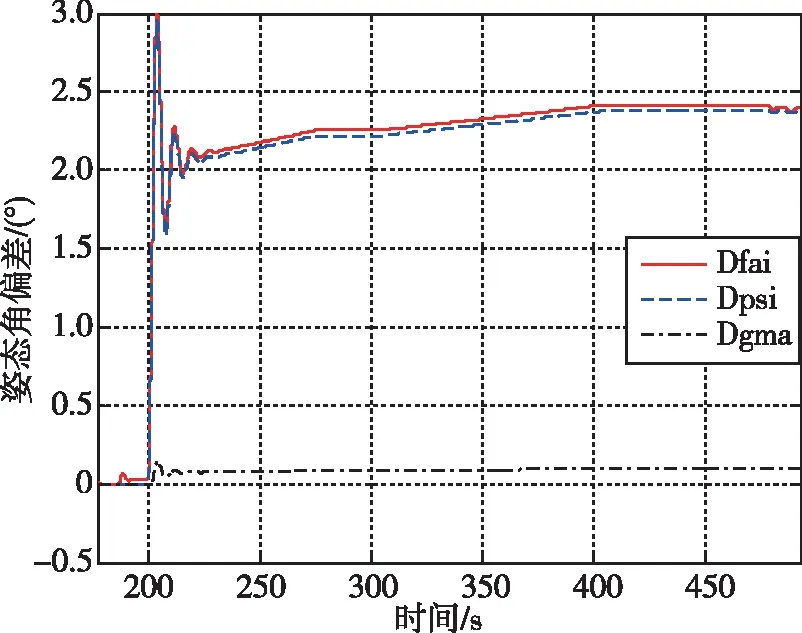
(a)姿态角偏差

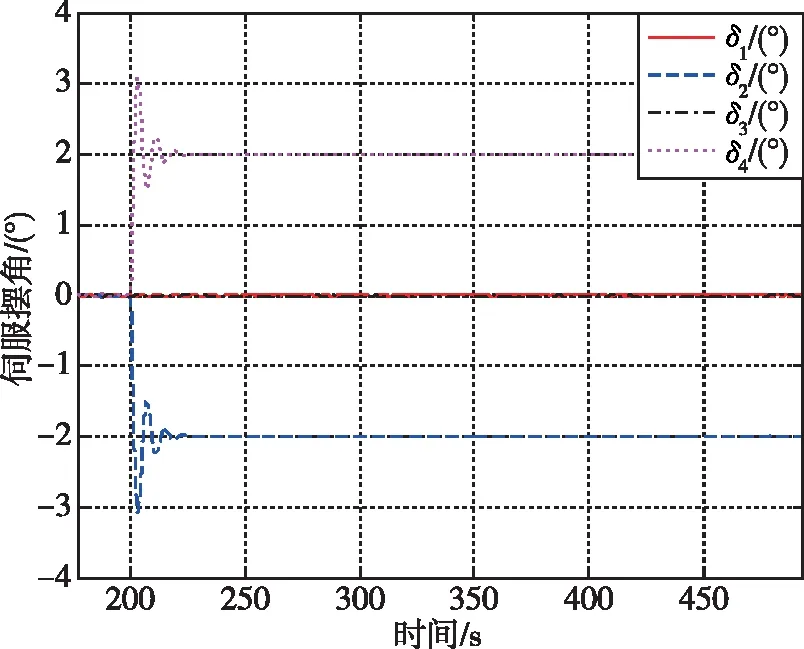
(b)伺服响应图8 布局1伺服机构δ2卡滞2°的控制配平结果Fig.8 Trim results of δ2≡2° for Layout-1

对于布局3，开展切向伺服机构δ2卡滞固定角度情形下的姿态仿真，图9为伺服机构II(切向摆动)卡滞2°故障情形下的姿态角偏差和伺服响应动态，为了配平将诱导出滚动控制力矩，伺服δ2和伺服δ4配平后将引起负的滚动力矩，因此诱导出负的滚动姿态角偏差来驱动伺服δ1产生负的摆角，伺服δ1的负摆角产生正的滚动力矩参与配平。由于没有采取控制重构措施，在PD控制作用下，需要配平卡滞角度造成的干扰，伺服机构卡滞将引起俯仰通道的静差，因此卡滞角度越大，那么对轨迹的影响越大。可见对于布局3，可较好地适应伺服机构卡滞的故障，此时可控的伺服机构数量与通道控制的自由度相同，具备配平条件。

(a)姿态角偏差

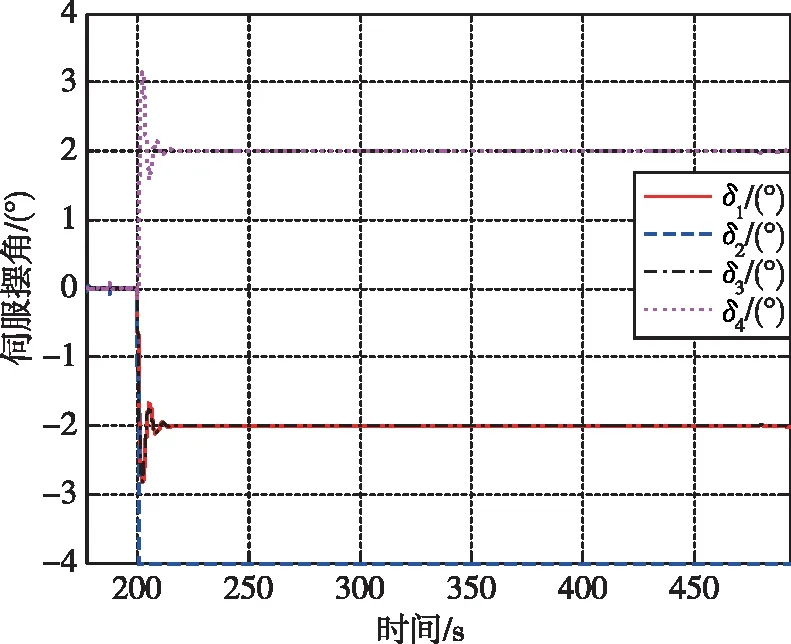
(b)伺服响应图9 布局3伺服机构δ2卡滞2°的控制配平结果Fig.9 Trim results of δ2≡2° for Layout-3

布局2发生伺服机构卡滞故障情形与布局1类似，不能适应切向伺服机构卡滞的情形，此时滚动通道丧失控制能力，姿态将迅速失稳；卡滞角度越大则姿态失稳越快；对于径向伺服机构卡滞故障，此时可控的伺服机构数量与通道控制的自由度相同，具备配平条件，姿控稳定。

布局4发生伺服机构卡滞故障情形与布局3类似，可较好地适应伺服机构卡滞故障，此时可控的伺服机构数量与通道控制的自由度相同，具备配平条件。因此，从适应伺服机构故障的情形来说，并联双机控制方案推荐采用布局3和4，可提高火箭对于伺服故障的适应能力。

3.4 并联双机布局分析

并联双机的不同布局方案故障配平仿真分析表明：正常飞行条件下，布局1和2等价，布局3和4等价，在相同的伺服最大摆动角度下，布局1和4通道最大控制能力是布局2和3的1.414倍；在推力故障条件下，布局1和2与布局3和4的差异在于配平角度的不同，其中布局2和4在推力故障下只在单一通道上形成干扰，这是比布局1和3优越的地方。当发生伺服机构卡滞故障时，姿控布局3和4可适应任意方向伺服机构卡滞，姿控布局1和2不能适应切向摆动伺服机构故障。综合以上配平仿真结果，并联双机摆发动机控制方案推荐使用布局4。

在此讨论的是不改变控制结构，即控制律和控制分配均按照正常工况设计，分析现有姿控方案故障的适应性。若采取控制重构措施，则可进一步提高姿控抗干扰能力，并克服故障引起的姿态角偏差，从而提高火箭的故障适应能力。而对于火箭真实飞行的控制情形，当存在结构干扰和其他未建模动态等综合控制效果后，故障后真实的飞行姿态动态过程是十分复杂的，需要针对具体情形考虑天地差异性，进行进一步研究。

4 控制重分配策略

为了实现运载器适应故障下的控制重构能力，将控制器的设计分解为控制律算法与控制分配模块，控制律可集成先进的鲁棒控制项或者自适应项，完成对干扰的估计与补偿，获得故障条件下的控制性能。控制分配模块则根据故障情况来实现最优的控制摆角指令分配，修正故障发生后原控制分配的不合理性。

对于采用多种/多个执行机构进行组合控制的运载器，其期望控制向量可写为

Mc=Bδc

(13)

根据期望控制向量Mc与控制效率矩阵B，求解实际控制指令δc的问题即为控制分配问题。

控制分配模块与火箭摆发动机控制的布局密切相关。不同火箭的摆发动机控制布局控制分配模块需要具体设计。以布局1为例，其正常工况下的控制分配设计模型为

(14)

当发动机故障时，控制效率矩阵B中与相应发动机推力相关的项将发生变化，当伺服机构发生故障时，体现为式(14)的某一行将发生变化。

故障下的摆角控制指令分配问题可归结为已知期望控制力矩Mc、干扰力矩Bfδc和故障后的控制效率矩阵Br，求故障后满足指定性能约束条件下剩余正常发动机摆角δc的问题。

因此可将控制分配问题转换为具有如下性能指标的有约束优化问题

(15)

一种工程可行的重分配控制策略是，当故障发生时，由式(16)可见，由于滚动通道的姿态角偏差Δγ不会进入俯仰和偏航通道，因此放宽滚动通道的控制性能可以有效提高俯仰与偏航通道的稳定边界，滚动通道只需要保证不是快速发散即可，从而避免滚动通道产生较大的摆角需求而使伺服饱和。通过调整加权系数矩阵W来获得不同需求的性能指标，从而更好地适应故障工况，无故障时伺服摆角优化分配的控制效果与原控制分配控制性能一致。

(16)

以布局1为例，按照3.2节的推力下降故障模式，图10给出了控制重分配后的姿态控制情况，结果表明，各伺服摆角均在4°以内，滚动姿态角偏差大于1°，由于故障发生后滚动通道的姿控能力仍然有效，此时控制重分配通过对分配矩阵加权的调整放宽了对滚动通道的姿控性能指标，与原控制分配相比，控制重分配充分利用了通道的耦合控制作用，适当降低姿控性能指标，从而满足稳定性和可用摆角的需求。

(a)姿态角偏差动态

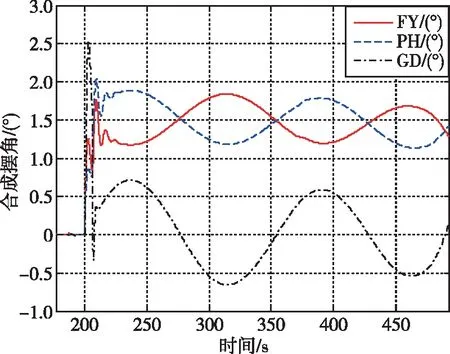
(b)通道合成摆角

(c)伺服响应图10 布局1发动机II剩余5%推力的控制重分配结果Fig.10 Re-allocation results of thrust II remaining 5% for Layout-1

以上基于优化的控制重分配设计中，从式(14)可知，控制重分配需要实时引入发动机的推力估计与火箭的质心估值，可采取在线与离线相结合的方式进行信息综合，火箭的质心可取飞行时段的平均值，发动机的推力可根据涡轮泵的转速与燃烧室的喷前压力进行估计。控制重分配作为容错控制技术的一种解析冗余方法获得了普遍的重视，基于动力学的方法由软件算法实现传统硬件的功能，充分利用箭上各种已有的导航、制导与控制信息，进行在线估计与综合，实现姿态控制系统对任务与故障的鲁棒性。

5 结论

针对典型的并联双机摆发动机控制布局，本文基于传统PD控制算法开展故障模式下的控制配平仿真比较研究。结果表明，不同的控制布局对故障的适应能力是不同的。正常工况下布局1与2的配平效果和稳定性一致，布局3与4的配平效果和稳定性一致。对于伺服机构摆动方向过箭体中心线的布局1和2，无法适应一台切向摆发动机卡滞的故障模式。在发生一台发动机零推力故障后，此时出现两个伺服机构控制3个通道的情形，姿态角速度将不能稳定，姿态发散的快慢与姿态角速度的初始扰动和干扰的大小相关；当故障发动机具有一定的残余推力作用时，在可用摆角范围内的4种布局姿控均是稳定的，布局2和4推力故障产生的初始扰动集中在单一通道，具有一定的优势。比对各摆发动机姿控布局对故障的适应性，建议将布局4作为设计优选的方向。在不改变控制律时，采用控制重分配策略可有效提高故障适应能力，放宽滚动通道控制性能可作为控制重分配的有效手段。