低轨巨型星座网络容量评估与分析

杨华果，陈 全，杨自鹏，张 群，吴 帅，杨 磊

(1.国防科技大学空天科学学院，长沙 410073；2.北京宇航系统工程研究所，北京 100076；3.军事科学院，北京 100091)

0 引言

近年来，卫星通信在民生等各领域发挥了重要作用。低轨卫星间可以通过建立星间链路形成卫星组网，低轨卫星网络可以提供广覆盖、低时延、大容量的通信服务和随遇接入的网络服务，且具有链路损耗少、成本低、布设不受影响等优点[1-3]，可提供不依赖地面网络的通信服务，有效弥补地面通信网络和高轨卫星网络的不足。

随着卫星通信技术的发展，发射成本逐渐降低，市场需求量不断扩大，低轨卫星网络向着巨型星座发展。近年来，“星链”(Starlink)、“一网”(OneWeb)和“柯伊伯”(Kuiper)等星座项目推动了低轨巨型星座的飞速发展[4]。本文研究的主要对象为低轨巨型星座网络，其网络通信图如图1所示，包含地面网络和卫星星座网络。地面网络由分布在各地的信关站和用户终端组成，卫星星座网络通过星间链路相连。

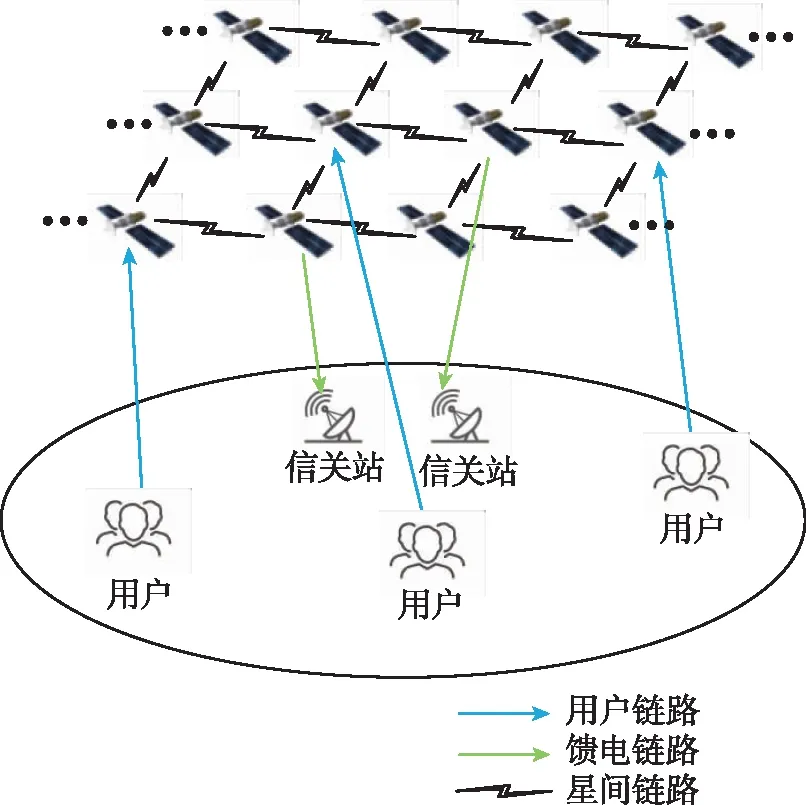
图1 低轨卫星网络通信图Fig.1 LEO satellite network communication

在低轨卫星网络的设计和建设中，卫星网络容量是网络性能评价的重要指标，反映网络的最大服务能力，可以为提高网络效率、设计高效的网络协议提供依据[5]。网络容量可定义为星间链路单位时间内传输的最大数据量，即网络能够承载流量的最大值。现有的卫星网络容量分析常采用仿真分析法、建模优化法和数值分析法[6]。文献[7]利用空间网络仿真平台分析了不同路由策略下的网络吞吐量。文献[8]建模了卫星通信系统最大化信道有效容量的功率分配问题，文献[9]建立了网络容量模型，并利用改进后的分布式遗传算法得出卫星网络容量上限。当前已有的方法应用于巨型星座仿真时大多计算复杂度高，耗时长，特别是利用网络仿真平台的方法对计算机硬件要求较高，且计算开销随网络节点数增大而迅速增加，在巨型星座网络评估中将产生巨大的计算开销。巨型星座规模的扩张不仅提升了系统容量，也增加了系统复杂度和性能评估难度。

因此，本文提出一种基于最大流的网络容量评估方法，通过求解最大流来替代网络路由仿真，从而有效减小巨型星座网络容量评估的复杂度与计算开销。最后基于“星链”星座，进一步研究了星座构型、星间链路拓扑连接方式、链路容量及用户需求量对巨型星座网络容量的影响。

1 基于最大流的低轨卫星网络容量评估模型

本文主要采用求解最大流的方法代替网络仿真来进行网络容量的评估。在给定网络规模下以最大流方法计算求解网络容量，分析网络容量与星座构型、星间链路拓扑连接方式及链路容量的关系。卫星之间通过建立星间链路来实现连通和通信，每颗卫星可建立2条、3条、4条或6条星间链路。星地下行链路的流量远大于星地上行链路，因此星地链路主要考虑下行链路。在进行仿真建模时，根据先验知识，综合考虑地面信关站的布局、链路容量及功率分配等参数对网络容量的影响，设定各参数值。

1.1 卫星网络模型

图2 低轨卫星网络星座构型图Fig.2 LEO satellite network constellation

卫星星座作为卫星网络研究的模型基础，决定着卫星网络的整个体系架构[10]。假设采用Walker-Delta星座构型，其构型如图2所示，轨道面个数为N1，每个轨道面上的卫星数量为N2。整个星座是均匀对称的，且不存在反向缝。基于图论方法，在卫星星座中，可将每颗卫星抽象为图的一个节点，相邻节点之间通过全双工链路实现通信，这种链路即为星间链路 ISL(Inter-Sate-llite Link)[11]，将星间链路抽象为图的边。依据相邻两节点是否在相同轨道面内，将星间链路分为轨内星间链路(intra-plane ISL)和轨间星间链路(inter-plane ISL)[12]。

卫星节点集为

S={a=(a1,a2)|0≤a1≤N1-1,
0≤a2≤N2-1}

(1)

其中，节点a代表位于第a1轨道上的第a2颗卫星。链路集为

(2)

其中，b=((a1±1)modN1，a2)时，链路(a，b)代表相邻轨道上第a2颗卫星间的链路；b=(a1，(a2±1)modN2)时，链路(a，b)代表同一轨道上相邻卫星间的链路。网络中的每颗卫星在水平和垂直方向上各有2个相邻节点，每颗卫星均采用一星四链的连接方式[13]，网络的局部拓扑如图3所示。

图3 卫星网络局部拓扑Fig.3 Satellite network partial topology

1.2 最大流算法原理

最大流问题是研究在给定条件下如何使网络流量达到最大值的组合优化问题[14]，其实质就是求解从源点到达汇点的流量最大值[15]。求解最大流能够为大规模网络的计算研究提供基础，其中一种经典的解法为增载轨算法[16]。

在给定网络中进行流量传输时每条链路的容量是固定值，当流量开始分配后，每条链路上的剩余容量都会随之改变。如果在从源节点到汇节点的一条链路中的每条边都存在非零的剩余流量，则将该条链路称为增广链。该条链上还能增加的流量由所有边中最小的剩余容量决定。增载轨算法就是在具有剩余容量的网络中沿可行路径增广流值，直至网络中不存在增广链时累加达到的可行流就是整个网络容量的最大值。

增广链的正确选择有利于提高计算效率，在进行增广链确定时需要首先确定一条从源节点到汇节点的通路，且该条链路每条边均具有剩余容量，然后对每个节点进行搜索，确定所有能到达的下一节点，直至得到包含所有节点的树，最终确定一条增广链。

在容量网络G=(V，A，c)中，将从源点s到汇点t的非负函数fst定义为可行流，假如fst满足以下条件[17]

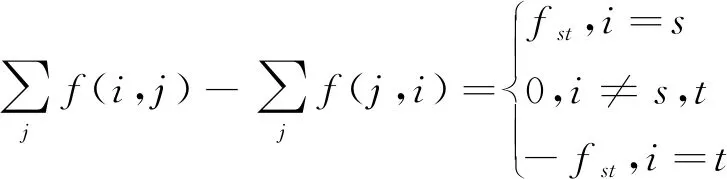
(3)

则fst成为容量网络G=(V，A，c)的全部可行流之一，当该流值为所有流中的最大值时则成为最大流，记为fmax。

1.3 基于最大流的网络容量评估模型

在实际运行过程中，星下用户密度不均且需求量不一致，会导致数据流量不一致，且不会一直保持饱和状态[6]，因此将所有用户虚拟为一个源节点，所有信关站虚拟为一个汇节点。源节点与所有卫星相连，汇节点与距离每个信关站最近的两颗卫星相连。由于卫星一直处于高速运动中，网络拓扑和网络容量都会随之产生动态变化，在仿真中可将卫星运行周期划分为多个时间片，假设在各时间片中网络拓扑为静态，分别求解各时间片的最大流，计算平均值作为最终的网络容量。

卫星网络最大流的模型示意图如图4所示。

图4 卫星网络最大流模型示意图Fig.4 Maximum flow model of satellite network

2 仿真算例

根据前文分析，以“星链”550 km轨道层星座的规模为例，进行具体仿真实验。在给定的网络规模下计算求解该网络的最大流。最后，分析网络容量与星座构型、星间链路拓扑连接方式及链路容量的关系。

2.1 网络容量求解

以“星链”550 km轨道层星座为基础研究对象，星座包含72个轨道面，且每个轨道面上有22颗在轨卫星。在计算网络容量时综合考虑星地连接约束、链路拓扑动态变化、链路容量约束。地面采用全球分布的30个信关站布局，仿真场景设置参考已有文献[18]。星座结构决定卫星间的相邻关系、星间链路数量和网络拓扑的变化方式[19-20]。在求解网络容量中，首先要获取低轨卫星星座的星座构型及其余各项参数，之后对每颗卫星进行编号，每颗卫星的所在位置与网络节点一一对应。将卫星运行周期按照链路特性及运动规律划分为多个时间片，在各时间片中将网络拓扑视为静态。确定星间链路连接方式后生成邻接矩阵，对矩阵进行赋值。若两颗卫星间有连接则矩阵中对应数值为1，否则为0。然后为每颗卫星计算用户流量输入，并确定卫星与信关站的连接状态。最后，对各时间片分别求解最大流，将各时间片下的最大流值求平均即为该卫星网络的网络容量。本文讨论的方法均是对一个时间片进行仿真验证，实际仿真过程中将仿真时间片设置为30 s，共仿真12 h，最后计算各时间片的网络容量平均值。

贪婪算法是通过组合局部最优解来构建全局最优解，在优化问题和网络分析等领域被广泛应用。为验证本文方法的正确性和有效性，本文首先采用了贪婪算法求解网络容量，并以“星链”550 km轨道层星座为研究对象，涵盖了72个轨道面，且每个轨道面上有22颗在轨卫星，每颗卫星均建立4条星间链路。该算法计算复杂度为O(n2)，其中n是输入规模，即总节点数。最大流算法的计算复杂度为O(mf)，其中m是图的边数，f是最大流的值。在本文设定的仿真规模条件下，最大流算法具有更低的计算复杂度。采用贪婪算法对网络进行仿真时，得到的计算数据与最大流算法的输出相同，验证了该算法的正确性和有效性，但是，贪婪算法的平均运行时间远大于最大流算法的平均运行时间，说明所提方法在巨型星座场景下的计算效率更高。两种算法的性能比较如图5所示。

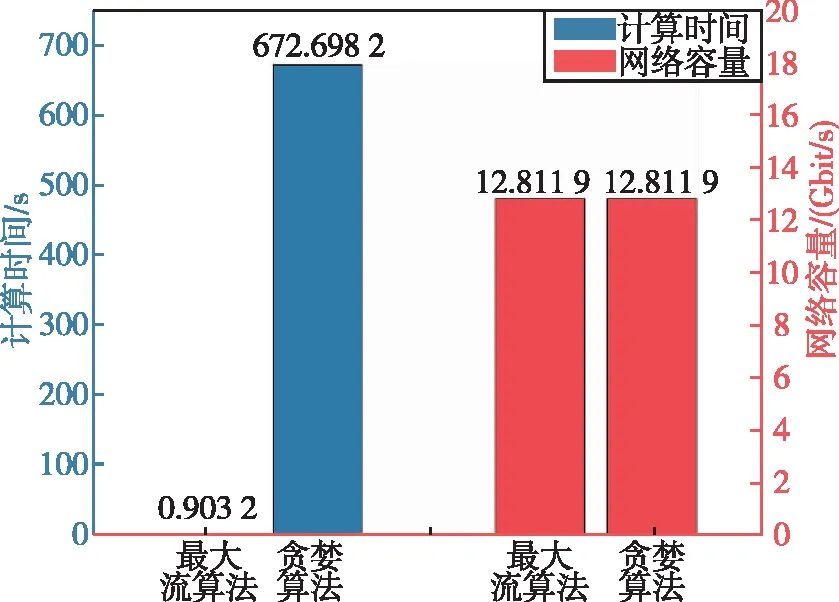
图5 两种算法的性能比较Fig.5 Performance comparison of two algorithms

2.2 不同星座构型下的仿真分析

“星链”550 km轨道层星座共有1 584颗卫星，假设每颗卫星均建立4条星间链路，即与其同轨前后和异轨左右的4颗相邻卫星建立星间链路。其中，每条轨道面上的第1颗卫星同第N2颗卫星建链，第一轨道面的卫星同第N1轨道面的卫星建链，形成无缝的均匀对称网络。假设每条星间链路容量为100 Mbit/s，用户需求总量为20 Gbit/s，信关站容量为2 Gbit/s。在保持星座卫星总数不变的情况下，改变轨道面数N1和每轨卫星数N2，得到不同的星座构型。不同星座构型下仿真得到的网络容量结果如表1所示。

表1 不同星座构型下的网络容量

由表1的仿真结果可知，在给定的星座规模中通过改变轨道数目和单轨卫星数可设计不同的星座构型，而不同配置的星座构型会导致网络性能的不同。仿真结果表明，当N1与N2相差值最小(N1=36，N2=44)时，网络容量达到最大。其成因可能是N1与N2更接近，星座的Mesh状拓扑均匀对称性更强，网络连接效率更高，导致更大的网络容量。

2.3 不同星间链路拓扑连接下的仿真分析

在给定规模的卫星网络中不同的拓扑连接方式将导致网络性能的不同。星座包含72个轨道面，且每个轨道面上有22颗在轨卫星，通过连接星间链路建立对称的网络。假设每条星间链路容量为100 Mbit/s，信关站容量为2 Gbit/s。本文选用的建链方式包括一星两链(2-ISL)、一星三链(3-ISL)、一星四链(4-ISL)和一星六链(6-ISL)。不同的建链方式如图6所示，仿真得到的网络容量结果如表2所示。

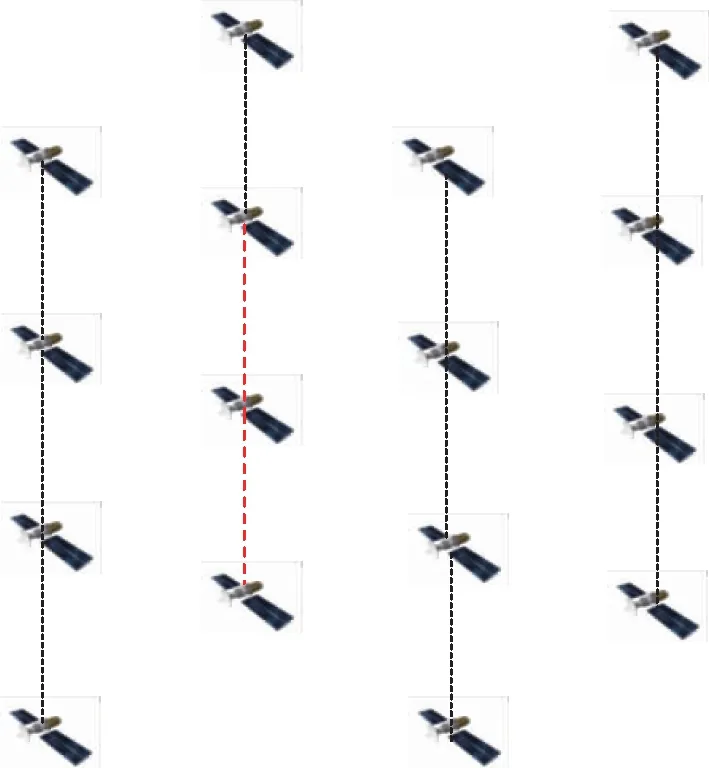
(a)一星两链

(b)一星三链

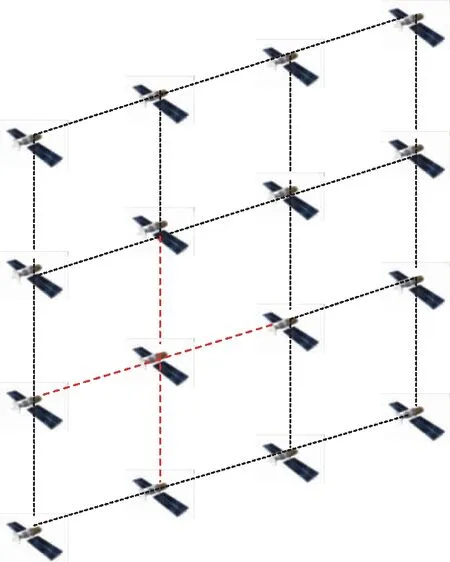
(c)一星四链

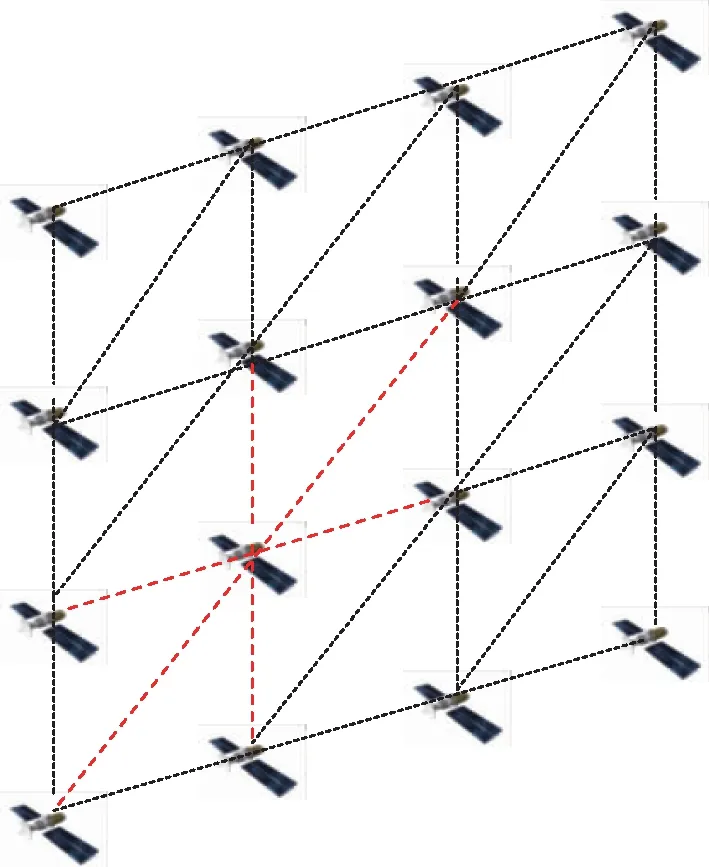
(d)一星六链图6 不同星间链路的拓扑示意图Fig.6 Topological diagrams of different inter-satellite links

表2 不同星间链路拓扑连接下的网络容量

由表2的仿真结果可以看出，在给定卫星数目和构型的星座内，卫星间建立的链路数目越多，网络容量越大。星间链路的增加可提升网络连接性，由于星间链路数目增加，同一时间单颗卫星可承载的数据量也增加，进而导致网络容量增大。考虑到星上体积功率受限以及星间通信终端的资源占用，单星可建立的星间链路数目也受限制，目前常见的构型一般采用3～4ISL构型。

2.4 不同链路容量参数下仿真分析

卫星网络系统中不同链路的容量差异也影响着整个网络的传输效率及网络容量。以“星链”星座550 km轨道层为研究对象，共有72个轨道面，且每个轨道面上都有22颗卫星。假设每颗卫星均采用一星四链的连接方式，用户需求总量为100 Gbit/s。改变星间链路容量，得到不同星间链路容量下的平均网络容量，如表3所示。

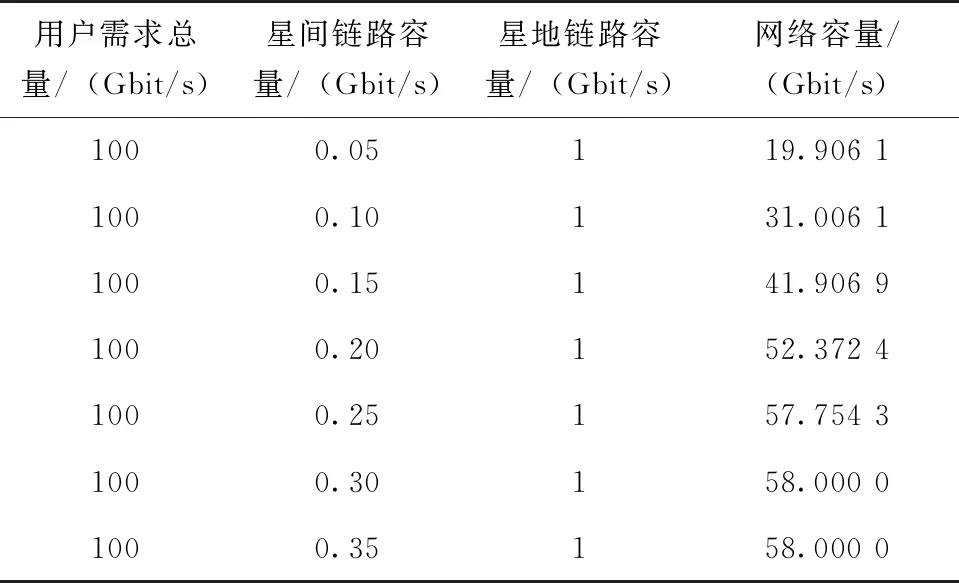
表3 不同星间链路容量下的网络容量

由表3的仿真结果可以看出，在卫星网络规模及星座构型确定的场景下，网络容量随星间链路容量的增加而增加，但当星间链路容量增加到一定值时，网络容量趋于平稳，不再增加。其原因是，卫星承载的流量来自其自身覆盖域内的业务量和周边卫星经星间链路转发的业务量。当星间链路容量较小时，星上流量受限于星间链路容量，将随着星间链路容量增加而增加，从而增加系统容量。当星间链路足够大时，星上业务量超出星地链路容量，限制了星上业务的星地传输，从而使得系统容量不再随着星间链路容量增加而增加。

仿真中保持其他链路容量不变，改变用户需求总量，得到不同用户需求量下的网络吞吐量结果，如表4所示。

表4 不同用户需求总量下的网络吞吐量

由表4的仿真结果可以看出，在卫星规模及星座构型确定的场景下，用户需求总量也将影响整个网络的吞吐量。当用户需求总量较少时，全部用户业务需求都可转发至信关站，此时网络吞吐量与用户需求量相等，随着用户需求量增长而快速增长。当用户需求总量较大时，受限于星间链路容量和星地链路容量，无法将所有数据下传至汇节点，此时网络吞吐量小于用户需求总量，且两者差值逐渐增大，网络吞吐量逐渐增大至星间链路/星地链路确定的网络容量上限。在本算例中，限制网络容量的主要参数为星间链路容量。

3 总结

本文研究了采用最大流算法求解低轨卫星网络容量，以“星链”星座为例，分别分析了在给定规模下不同的星座构型、星间建链数与链路容量参数对网络容量的影响。与传统网络容量评估方法相比，计算复杂度更低，计算耗时更短。根据仿真结果可知，网络容量与星间建链数和星间链路容量呈正相关。此外，网络容量还受星座构型和用户需求总量等参数的影响。在设计通信网络时可以考虑增加星间链路数，以提高整个网络效率。